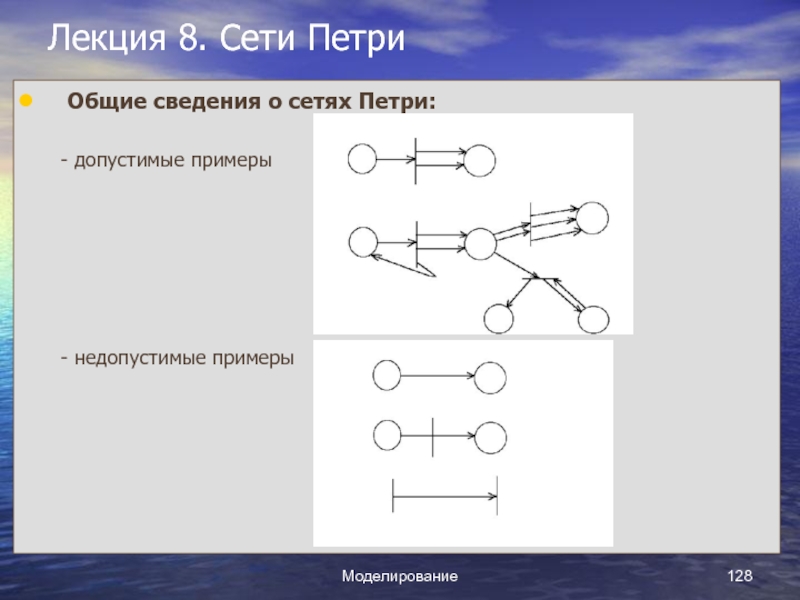
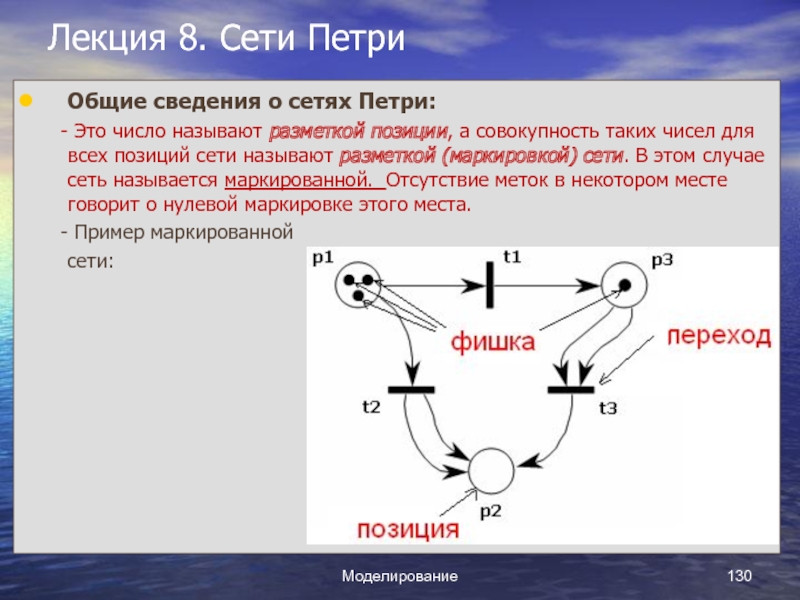
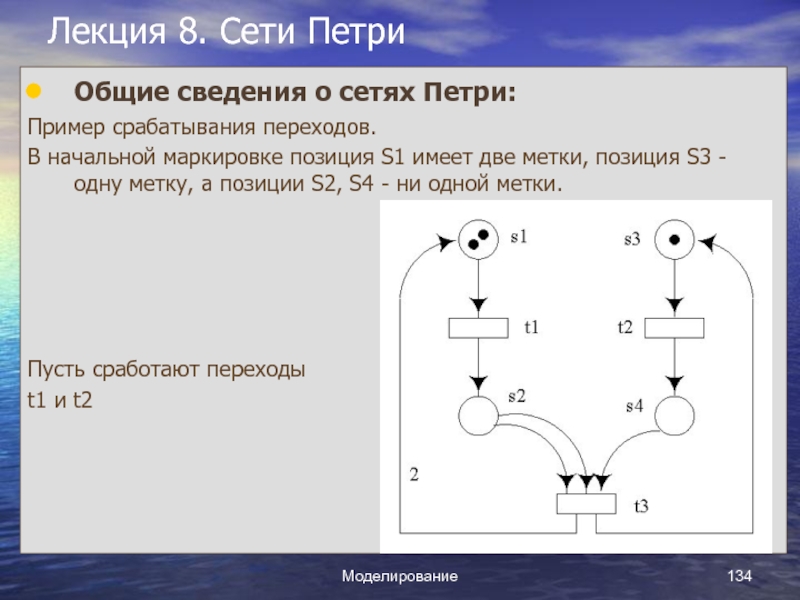
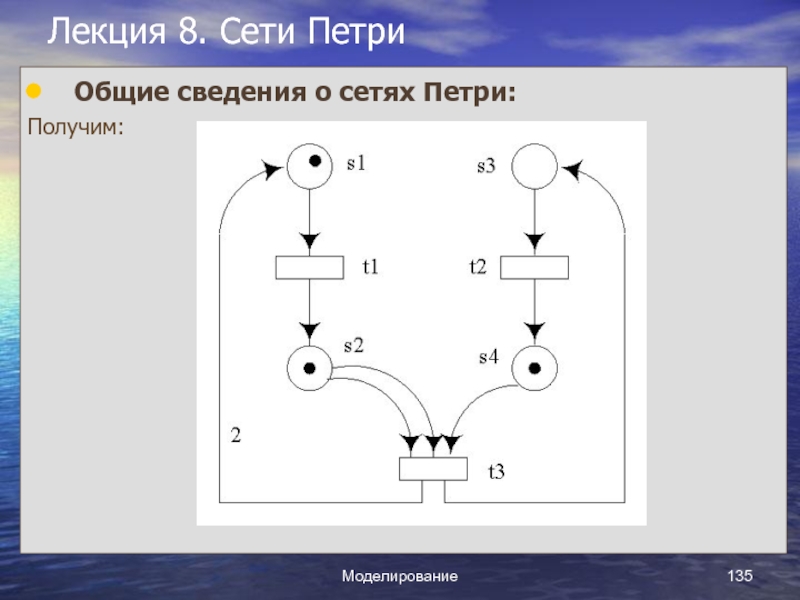
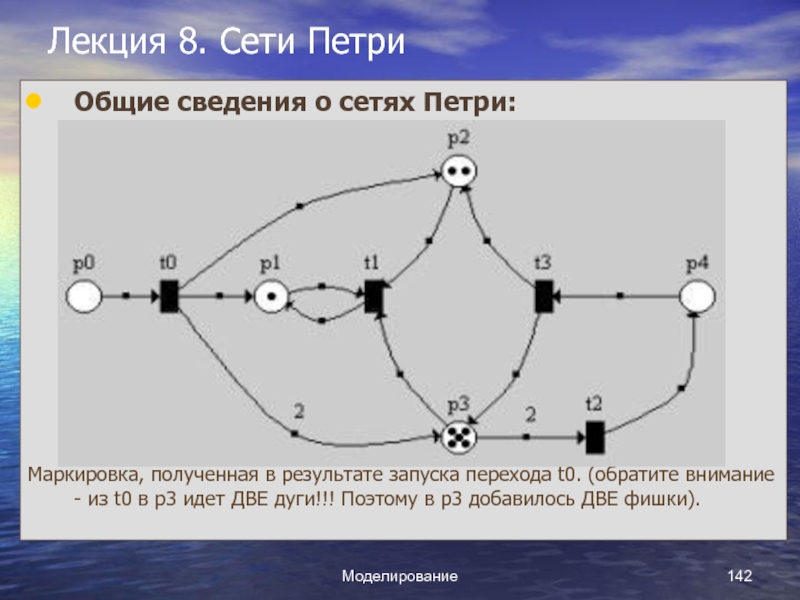
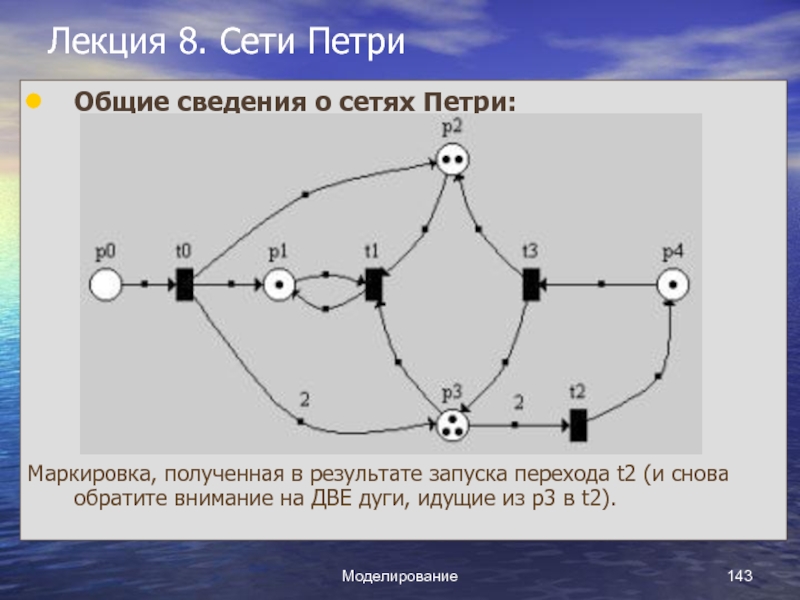
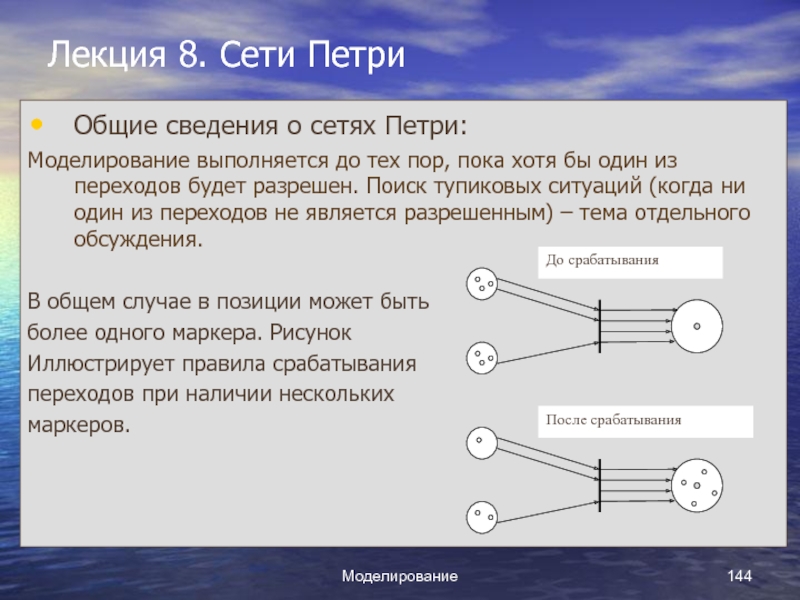
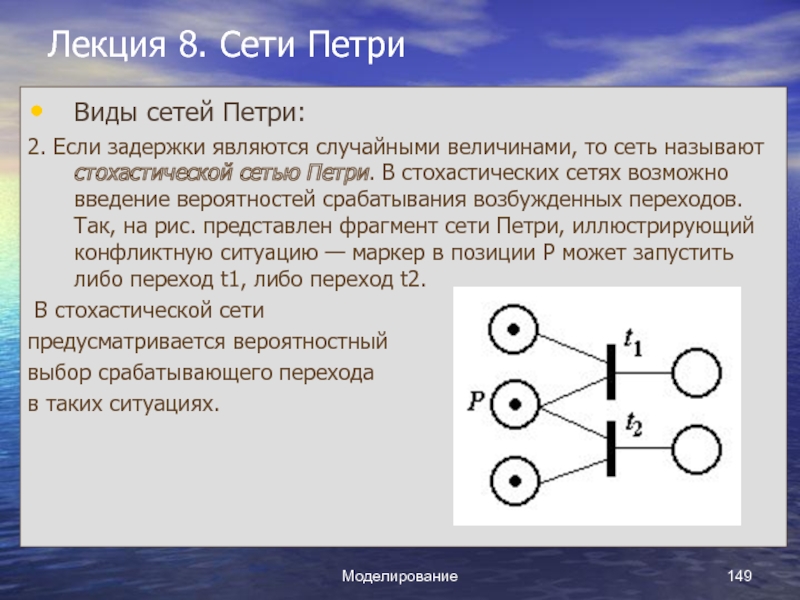
Слайд 1Курс
«Моделирование»
Эмблема
Лектор – Ланцов Владимир Николаевич, кафедра ВТ
Слайд 2Моделирование
Состав курса:
Лекции – 36 ч.
Лаборат. работы – 18 ч. (4
работы с 9-й нед.)
Практические – 36 ч.
К.Р. - нет
Экзамен
– есть
Рейтинг-контроль
6 неделя – по лекциям
12 неделя – по практическим + лекциям
17 неделя – по практическим + лаб.работам + лекциям
Слайд 3Моделирование
Содержание лекций
Лекция 1. Общие сведения о моделировании.
Лекция 2. Моделирование ВС
с помощью систем массового обслуживания.
Лекция 3. Организация моделирования СМО.
Лекция 4.
Модели источников входного потока заявок.
Лекция 5. Языки имитационного моделирования.
Лекция 6. Планирование машинного эксперимента.
Лекция 7. Аналитическое моделирование.
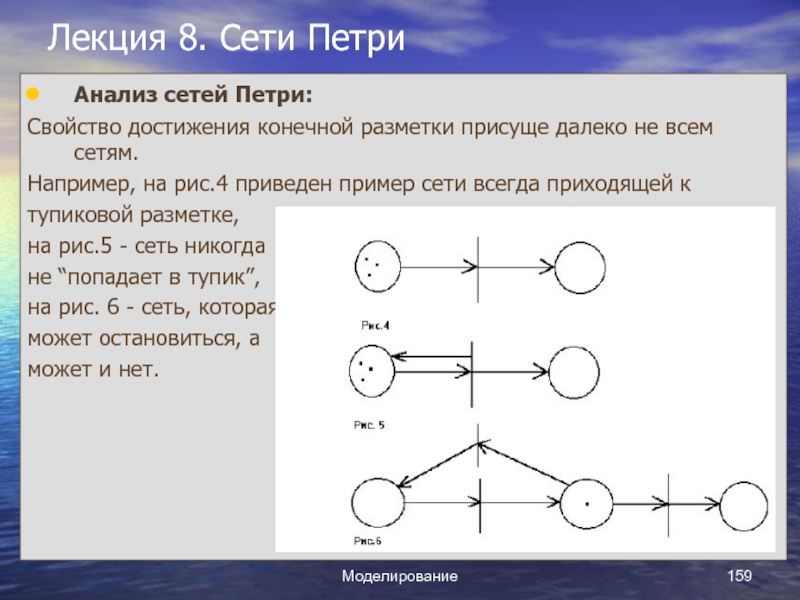
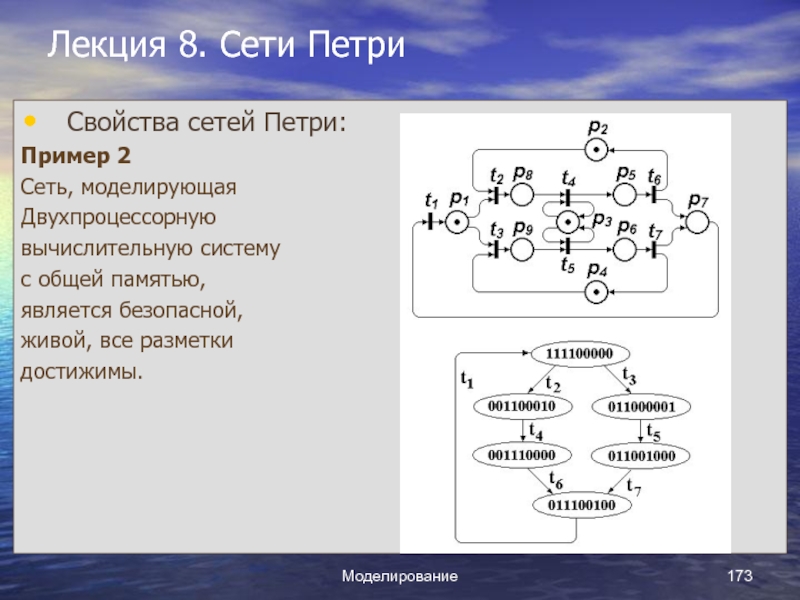
Лекция 8. Сети Петри.
Лекция 9. Цепи Маркова.
Слайд 4Моделирование
Литература
Основная:
1. Ланцов В.Н. Моделирование. Часть 1. /уч.пособие. – ВлГУ, 1999
2.
Советов Б.А., Яковлев С.А. Моделирование систем. – М.: Высш.шк., 1985
3.
Петерсон Дж. Теория сетей Петри и моделирование систем: Пер. с англ. – М: Мир, 1984
Дополнительная:
4. Ланцов В.Н. Моделирование. Часть 2. /уч.пособие. ВлГУ, 2001
5. Шрайбер Т.Д. Моделирование на GPSS. – М.: Машиностроение, 1980
Котов В.Е. Сети Петри. – М: Наука, 1984
6. Советов Б.Я., Яковлев С.А. Модедирование систем: Лабораторный практикум.-М.: Высш.шк., 1989
Слайд 5Моделирование
Лекция 1. Общие сведения о моделировании
Содержание:
Введение
Основные определения теории моделирования
Классификация математических
моделей
Методика получения математических моделей элементов
Обобщенная схема моделирования
Слайд 6Моделирование
Лекция 1. Общие сведения о моделировании
Введение:
Необходимость внедрения средств ВТ в
различные отрасли н/х
Требования к уровню подготовки специалистов повышаются, необходимы знания
по методикам анализа и моделирования на базе современных программных систем
Полное и всестороннее исследование ВС возможно только с помощью средств моделирования
«Моделирование» базовая дисциплина специальности, отдельный раздел дипломных и курсовых проектов
Слайд 7Моделирование
Лекция 1. Общие сведения о моделировании
Основные определения теории моделирования:
Объект моделирования
– все, на что направлена деятельность человека
Гипотеза – предсказание, основанное
на небольшом количестве опытных данных
Аналогия – суждение о частном сходстве двух объектов. Часто гипотеза создается по аналогии.
Наглядная и удобная форма для сравнения и представления гипотез и аналогий – объекты-заменители для объектов-оригиналов (модели)
Моделирование – это замещение одного объекта другим сцелью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-заменителя (модели)
Теория моделирования – теория замещения одних объектов другими объектами (моделями) и исследование свойств объектов на их моделях.
Слайд 8Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Основные определения теории моделирования
(продолж.):
- Если результаты моделирования подтверждаются (свойства совпадают), могут служить основой
для прогнозирования процессов, то говорят, что модель адекватна объекту. Адекватность сильно зависит от цели моделирования и принятых критериев.
- Более обобщенно - моделирование это метод опосредованного познания объекта-оригинала.
Различают:
- моделирование как познавательный процесс обработки информации из внешней среды;
- моделирование как построение системы-модели (второй системы), связанной определенными соотношениями подобия с системой-оригиналом (первой системой).
Слайд 9Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Основные определения теории моделирования
(продолж.):
- ВС и комплексы относятся к одним из самых сложных
систем. Проектирование и исследование их невозможно без использования различных видов моделирования.
- На всех уровнях представления ВС учет особенностей: сложность структуры, неоднозначность связей между элементами, неоднозначность алгоритмов поведения при различных условиях, большое количество параметров и переменных, неполнота и недетерминированность исходной информации, разнообразие и вероятностный характер воздействий, стохастичность связей и т.д.
- На разных этапах применение метода моделирования преследует конкретные цели, а эффективность метода зависит от того, насколько грамотно разработчик использует возможности моделирования.
Слайд 10Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Основные определения теории моделирования
(продолж.):
- Выделяют два подхода:
аналитический и численный.
Аналитический - основан
на использовании формальных методов доказательств и решения в аналитическом виде, где модель представляется аналитическими зависимостями, а решение находится в явном виде.
Находит все меньшее применение, значительные трудности при моделировании сложных систем, упрощение моделей - к получению недостоверных результатов.
Численный подход основан на математическом моделировании процессов функционирования объектов. Математическое моделирование – это исследование объекта путем создания его математической модели и оперирования этой моделью с целью получения полезной информации о свойствах объекта.
Математическая модель – это совокупность математических объектов (чисел, скалярных переменных, векторов, графов и т.п.) и связывающих их отношений.
Альтернативой математического моделирования является физическое макетирование. У математического моделирования ряд преимуществ: меньшие сроки на подготовку моделирования; значительно меньшая материалоемкость, особенно при моделировании крупногабаритных объектов; возможность выполнения экспериментов на критических режимах, которые привели бы к разрушению физического макета и др.

Слайд 11Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Основные определения теории моделирования
(продолж.):
-В зависимости от характера изучаемых процессов все виды моделирования могут
быть разделены на:
Детерминированное моделирование отображает детерминированные процессы, т.е. отсутствие всяких случайных воздействий;
Стохастическое моделирование отображает вероятностные процессы и события, оцениваются средние характеристики.
Статическое моделирование служит для описания поведения объекта в какой-либо момент времени.
Динамическое моделирование отражает поведение объекта во времени.
Дискретное моделирование служит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, а дискретно-непрерывное моделирование используется в случаях, когда хотят выделить наличие как дискретных, так и непрерывных процессов.
Слайд 12Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей:
Представим модель
в виде
Y(t) = F(X, Q, t).
(1)
Где Х - совокупность (в общем случае вектор) входных воздействий и воздействий внешней среды; Q - совокупность внутренних (собственных) параметров системы; Y - совокупность выходных характеристик системы. Входные воздействия, воздействия внешней среды и внутренние параметры - являются независимыми переменными, а выходные характеристики являются зависимыми переменными. Процесс функционирования системы описывается оператором F, который преобразует независимые переменные в зависимые
Соотношение (1) является математическим описанием поведения объекта моделирования во времени t, т.е. отражает его динамические свойства. Поэтому модели такого вида назыв. динамическими моделями. Для статических моделей соотношение (1) преобразуется в
Y = F(X, Q).
Если математическое описание не содержит элементов случайности или они не учитываются, то модель называется детерминированной
Y(t) = F(X, t).
Детерминированная модель является частным случаем стохастической модели.
Слайд 13Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
Слайд 14Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
-
Структурная ММ отображает геометрические и топологические (структурные) свойства (формы и
взаимное расположение, состав и взаимосвязи). Представляется в виде уравнений поверхностей и линий, графов, таблиц, списков, неравенств и т.д.
- Функциональная ММ отражает физические и информационные состояния и процессы, последовательно сменяющих друг друга состояний в объекте. Типичная форма представления - системы уравнений.
При использовании блочно-иерархического подхода приводит к появлению деления моделей на уровни описания. Количество иерархических уровней определяется сложностью объектов и возможностями систем моделирования. Однако для большинства предметных областей в технике можно выделить три обобщенных уровней:
Микроуровень
Макроуровень
Метауровень,
различающихся степенью детализации рассмотрения процессов в объекте.
Слайд 15Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
ММ
на микроуровне отражает физические процессы, протекающих в непрерывных пространстве и
времени (сплошная или трехмерная среда).
Типичные ММ на микроуровне - системы дифференциальных уравнений в частных производных (ДУЧП) с заданными краевыми условиями. Независимыми переменными здесь являются пространственные координаты и время (уравнения Ламе для механики упругих сред, уравнения Навье-Стокса для гидравлики, уравнения теплопроводности для термодинамики и т.д.).
Для решения этих уравнений используются методы конечных разностей и граничных элементов. Возможно единое ПО для разных классов объектов.
Для элементов ВС модели описывают состояние в сплошной среде элементов и деталей узлов ЭВМ. Математическая модель – в виде ДУЧП (уравнения теплопроводности, диффузии, электродинамики, упругости, непрерывности, переноса, Пуассона и т.п.) с заданными краевыми условиями. В качестве переменных этих уравнений используются время t и пространственные координаты xi. Зависимыми параметрами являются температура, концентрация основных и неосновных носителей, напряженности полей и т.д.
ДУЧП можно представить в общем виде как
L φ(Z) = f(Z),
где Z = (t, x1, x2, x3,…) – вектор независимых параметров; f(Z) – внешнее воздействие на сплошную среду; L – оператор дифференцирования; φ(Z) – уравнение, описывающее физическую природу рассматриваемого объекта.
Если из уравнения исключить время t, то уравнение будет стационарным. Вместо трех пространственных координат можно использовать одну или две.

Слайд 16Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
Пример:
уравнение теплопроводности. Это уравнение является нестационарным и одномерным
ðТ/ðt – αt
* ð²Т/ðx² = 0,
где Т – температура, L = ð /ðt – αt * ð²Т/ðx² , φ(Z) = T(t,x),
f(Z) = 0, Z = (t,x).
Возможности ММ в виде ДУЧП ограничены отдельными компонентами (фрагментами). С увеличением размерностей решаемых задач анализ ММ на микроуровне приводит к чрезмерным вычислительным затратам, поэтому вводят какие-либо упрощения или допущения и переходят к следующему уровню описания. Осуществляется переход от непрерывного к дискретному пространству при сохранение непрерывного времени.
Слайд 17Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
-
На макроуровне используют укрупненную дискретизацию пространства по функциональному признаку, что
приводит к представлению ММ на этом уровне в виде систем обыкновенных дифференциальных уравнений (ОДУ) с заданными начальными условиями.
- В этих уравнениях независимой переменной является время, а зависимыми переменными являются переменные, характеризующие состояние укрупненных элементов, например силы и скорости механических систем, напряжения и силы тока электрических систем, давления и расходы гидравлических и пневматических систем и т.п.
- Системы ОДУ строятся на основе компонентных уравнений для дискретных элементов и топологических уравнений, указывающих связи между элементами. На этом уровне возможно единое математическое и программное обеспечение для разных классов технических объектов.
Слайд 18Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
-
Для узлов ЭВМ непрерывные модели формируются на основе компонентных, например:
i(t)
= U(t)/R, i(t) = C dU/dt, U(t) = L di/dt
- Используя топологические связи (например, для метода узловых потенциалов), можно получить систему дифференциальных уравнений:
F(U‘,U,t) = 0, где U‘ = dU/dt или U‘ = f(U,t)
- Для дискретных моделей на макроуровне все состояния дискретны, в частном случае это булевы переменные (0, 1). Непрерывное время также заменяется на дискретные значения (такты моделирования): Δtk = tk – tk-1
- Модель может быть представлена в виде конечного автомата, который описывается с помощью системы логических уравнений, например: V‘ = F(V, U).
Слайд 19Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
-
При повышении размерностей решаемых уравнений (порядок систем ОДУ превышает 103,
оперировать моделью становится затруднительным, и поэтому обычно переходят к следующему, более высокому уровню.
- На метауровне в качестве элементов принимают достаточно сложные совокупности компонентов. В моделях отражаются процессы преобразования информации, а не сигналов, как на макроуровне.
- Метауровень характеризуется большим разнообразием типов используемых ММ. Применяют:
системы ОДУ (с переменными, относящимися к выводам компонента)
функциональное моделирование, развитое для анализа систем автоматического управления (САУ)
моделями систем массового обслуживания (СМО)
сети Петри.
Слайд 20Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
-
Полная ММ – модель, в которой фигурируют переменные, характеризующие состояния
всех имеющихся межэлементных связей (т.е. состояния всех элементов объекта).
- Макромодель - ММ, в которой отображаются состояния значительно меньшего числа межэлементных связей, что соответствует более укрупненному описанию объекта. Понятия "полная ММ" и "макромодель" относительны.
- Аналитические ММ представляют собой явные аналитические выражения, связывающие выходные параметры с входными и внутренними параметрами.
- Алгоритмические ММ выражают связи выходных параметров с внутренними и внешними параметрами в виде алгоритма.
- Имитационная ММ отражает поведение объекта при заданных, изменяющихся во времени внешних воздействиях.
Слайд 21Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Классификация математических моделей (продолж.):
-
Математические модели разделяются на математические модели компонентов (элементов) и математические
модели систем (строятся на основе математических моделей компонентов).
- Теоретические ММ создаются в результате исследования процессов и их закономерностей, присущих рассматриваемому классу объектов и явлений.
- Эмпирические ММ - в результате изучения внешних проявлений свойств объекта с помощью измерений и обработки результатов измерений.
- Для большинства технических объектов используют типовые элементы, количество типов которых обычно невелико, а модели предназначены для многократного использования. Поэтому разработка ММ элементов выполняется сравнительно редко. Единожды созданные ММ элементов в дальнейшем многократно используются при разработке разнообразных систем на базе этих элементов. Типичные примеры - модели транзисторов и диодов, модели стандартных микросхем и т.п.
- Математические модели систем строятся на основе формальных правил или алгоритмов и часто выполняются в автоматическом режиме по математическим моделям компонентов. Изучение этих методов - одна из целей данного курса.

Слайд 22Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Методика получения математических моделей
элементов:
Процедура получения ММЭ включает в себя следующие операции:
1. Отбор свойств
объекта, которые подлежат отражению в модели (анализ возможных применений модели).
2. Сбор исходной информации о выбранных свойствах объекта (опыт и знания инженера, научно-техническая справочная литература, описания прототипов, близкие по своим свойствам имеющиеся ММ, результаты экспериментальных измерений параметров и т.п.)
3. Синтез структуры ММ (общий вид математических соотношений без конкретных числовых значений параметров, эквивалентные схемы, графы и т.п.). Это наиболее ответственная операция.
4. Расчет числовых значений параметров ММ с помощью минимизации погрешности между поведением модели и результатами эксперимента либо физического, либо численного с использованием более точных ММ.
5. Оценка точности и адекватности (области адекватности) ММ. Для оценки точности используются экспериментальные значения, не применявшиеся при четвертой операции.
Слайд 23Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
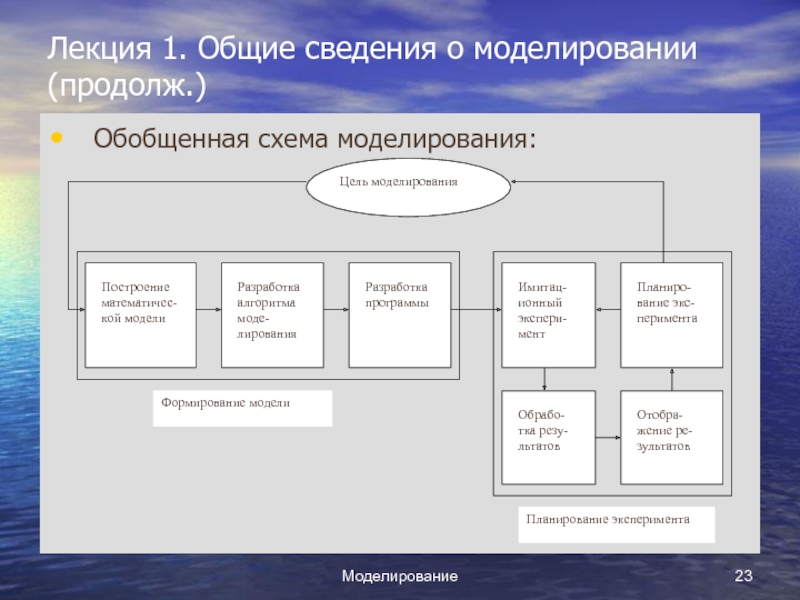
Обобщенная схема моделирования:
Слайд 24Моделирование
Лекция 1. Общие сведения о моделировании (продолж.)
Обобщенная схема моделирования (продолж.):
-
На первом этапе моделирования решается ряд задач: построения модели, выбора
алгоритма моделирования и программная реализация. Основным назначением первой задачи является переход от содержательного описания объекта к его математической модели.
- Второй этап моделирования – выполнение машинного эксперимента, рабочих расчетов по составленной и отлаженной программе. Здесь решаются задачи: планирования машинного эксперимента с моделью (начальные условия, число прогонов модели), проведение рабочих расчетов (исходные данные, получение результатов), анализ результатов моделирования (отбор, статистика), представление результатов моделирования (таблицы, графики, схемы), интерпретация результатов моделирования (интерпретация по отношению к моделируемому объекту), подведение итогов моделирования и выработка рекомендаций (выводы, проверка гипотез, рекомендации по использованию).
Слайд 25Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания
Содержание:
Задачи и
особенности системного уровня
Краткие сведения о СМО
Схема имитационного моделирования
Имитационные модели ВС
в СМО
Слайд 26Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания
Задачи и
особенности системного уровня:
- На системном уровне разрабатываются структурные схемы ЭВА,
в связи с чем данный уровень называют структурным уровнем.
- Ведется укрупненное рассмотрение всей ЭВМ или ВС в целом. Элементы – это крупные узлы ЭВМ (процессоры, каналы, запоминающие устройства, периферийные устройства), хотя степень детализации может быть и очень глубокой.
- С алгоритмической позиции – это разработка архитектуры ЭВА (форматы представления различных данных, системы и форматы команд, организация адресации; принципы выполнения операций, приоритеты, дисциплины обслуживания; общие технические характеристики ЭВА (производительность или пропускная способность, надежность и др.).
Слайд 27Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания
Задачи и
особенности системного уровня:
Основные задачи:
1) Определение принципов организации ВС.
2) Выбор архитектуры
и разделение функций на программную и аппаратную реализацию.
3) Разработка структурной схемы ВС.
4) Определение требований на выходные параметры и характеристики компонентов, формирование ТЗ на отдельные компоненты ВС.
Слайд 28Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Задачи
и особенности системного уровня:
Особенности системного моделирования:
- Функционирование ВС рассматривается с
информационной точки зрения (процесс преобразования информации), абстрагирование от физической сущности протекающих в системе процессов.
- Характер информационных процессов в ВС в значительной мере определяется программным обеспечением (совокупность аппаратных и программных средств).
- Моделирование выполняется как многовариантный анализ: варьируя характеристиками элементов и связями между ними, определяют такую структуру ВС, которая обладает заданными (необходимыми) характеристиками.
- Задачи моделирования отличаются большим разнообразием и трудно поддаются формализации, трудно автоматизировать процедуру составления математических моделей ВС на основе моделей компонентов.
- В ЭВМ с помощью математических моделей имитируется процесс ввода, обработки и вывода данных (метод имитационного моделирования).
- Соответствие ВС своему назначению невозможно проверить на примере одной задачи, решаемой в ВС. Необходимо обобщение на весь класс решаемых задач. Такое обобщение достигается при учете статистических закономерностей поступления и обработки данных, т.е. используются вероятностные методы.
- Наиболее часто ВС моделируются с позиций систем массового обслуживания (СМО).
- Возможна постоянная детализация моделей ВС. Число уровней детализации может быть очень большим.

Слайд 29Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Краткие
сведения о СМО:
- Системы массового обслуживания (СМО) – класс математических
схем для формализации процессов функционирования систем на основе процессов обслуживания.
- В качестве процесса обслуживания могут быть представлены различные по своей физической природе процессы функционирования экономических, производственных, технических и других систем, например: потоки поставок продукции некоторому предприятию, потоки деталей и комплектующих изделий на сборочном конвейере цеха, заявки на обработку информации в ЭВМ. Характерным для работы таких объектов является случайное появление заявок (требований) на обслуживание и завершение обслуживания в случайные моменты времени, т.е. стохастический характер.
- Элементы СМО:
СМО - это системы, предназначенные для обслуживания (обработки) потока заявок (решаемых задач) с помощью совокупности устройств (обслуживающих аппаратов - ОА).
- ОА относятся к так называемым статическим объектам или ресурсам. Такими объектами могут быть ЭВМ, отдельные устройства ЭВМ, внешние устройства и т.п. Так как обработка данных может выполняться как аппаратными, так и программными средствами, то программные средства также относят к ресурсам.
- Элементы динамического типа – это заявки, или транзакты (решаемые в ВС задачи).

Слайд 30Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Краткие
сведения о СМО (продолж.):
Элементы СМО (продолж.):
- Функционирование СМО – это
процесс прохождения заявок через ОА.
- ОА может быть в состоянии «занято» (если заявка вошла в ОА на обслуживание) или «свободно». ОА также характеризуется длиной очереди заявок к нему.
- Заявки характеризуются состояниями «на обслуживании» (если она занимает ОА) и «в ожидании» (если она находится в очереди).
- Дисциплина обслуживания – это правило, по которому заявки поступают из очереди на обслуживание в ОА. Наиболее распространенные: FIFO (first input – first output), «первым пришел – первым обслужен», LIFO (last input – first output) – здесь заявки выбираются из конца очереди.
Слайд 31Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Краткие
сведения о СМО (продолж.):
Элементы СМО (продолж.):
- Приоритет – это преимущества
на обслуживание одной заявки перед другими. Если все заявки имеют одинаковый приоритет, то система называется бесприоритетной.
- Приоритеты могут быть динамическими и статическими в зависимости от того, возможно или нет изменение приоритетов в процессе выполнения задачи.
- Любое изменение в состоянии системы является событием. Считается, что события происходят мгновенно в дискретные моменты времени.
- СМО могут быть одно- и многоканальные в зависимости от числа параллельно работающих каналов. Замкнутые СМО – это когда в системе циркулирует постоянное число заявок.
Слайд 32Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
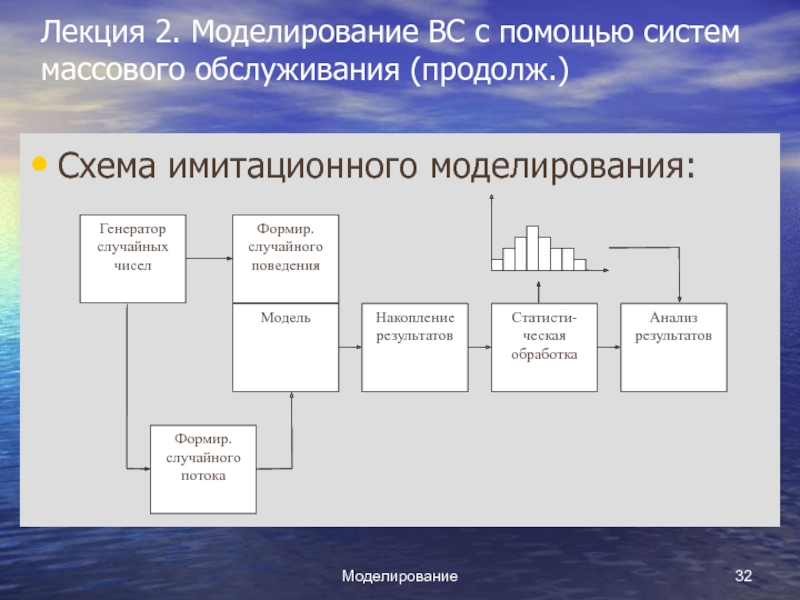
Схема
имитационного моделирования:
Слайд 33Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Имитационные
модели ВС в СМО:
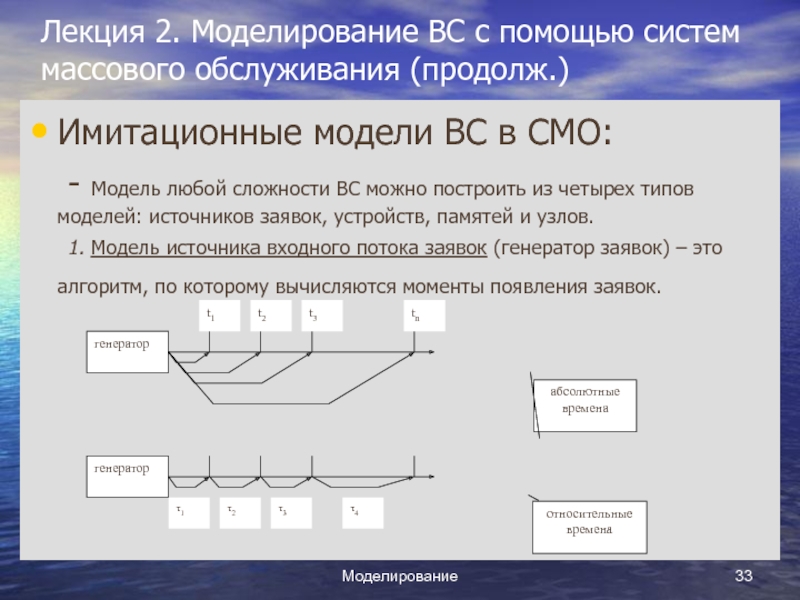
- Модель любой сложности ВС можно построить
из четырех типов моделей: источников заявок, устройств, памятей и узлов.
1. Модель источника входного потока заявок (генератор заявок) – это алгоритм, по которому вычисляются моменты появления заявок.
Слайд 34Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Имитационные
модели ВС в СМО:
2.Модель устройства – это алгоритм выработки значений
интервалов (времени) обслуживания заявки в данном устройстве. Чаще всего это алгоритм выработки значений случайной величины, распределенной по заданному закону.
Слайд 35Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Имитационные
модели ВС в СМО:
3. Модель памяти – это алгоритм, определяющий
объем памяти, необходимый для обслуживания заявки Vi. Обычно объем памяти определяется как реализация случайной величины, причем закон распределения и его параметры зависят от типа заявки.
Слайд 36Моделирование
Лекция 2. Моделирование ВС с помощью систем массового обслуживания (продолж.)
Имитационные
модели ВС в СМО:
4. Модель узла. Связи источников и ОА
в значительной мере определяются функционированием программного обеспечения (ПО), а не физическими связями между различными устройствами. Именно ПО определяет маршрут прохождения заявок по ВС. Для имитации связей используются специальные элементы-модели, называемые узлами. Модели узлов бывают нескольких типов, например: для организации разветвлений в зависимости от типа заявки или определенных признаков; для организации вероятностных разветвлений; для изменения типа заявок и др.
Слайд 37Моделирование
Лекция 3. Организация моделирования СМО
Содержание:
Организация моделирования в СМО
Событийное моделирование
Принципы работы
имитационных моделей
Организация программного обеспечения систем имитационного моделирования на основе СМО.
Слайд 38Моделирование
Лекция 3. Организация моделирования СМО
Организация моделирования в СМО:
- Имитационная
модель представляет собой алгоритм, состоящий из упорядоченных обращений к моделям
элементов. Последовательность обращений определяется свойствами моделируемой ВС и режимом ее функционирования.
- В процессе имитации в модели происходит изменение дискретного времени. Время изменяется после того, как заканчивается имитация очередной группы событий, относящихся к текущему моменту времени.
- В процессе имитации происходит накопление данных. Процесс имитации заканчивается, когда текущее время превысит заданный отрезок времени моделирования или когда входные источники выработают заданное количество заявок.
Слайд 39Моделирование
Лекция 3. Организация моделирования СМО
Организация моделирования в СМО:
- Организация
имитационного моделирования ВС будет заключаться в определении происходящих в системе
событий и их привязки к моментам дискретного времени и элементам системы.
- Математическая модель ВС представляет собой программу, включающую ряд подпрограмм. Ряд основных подпрограмм обеспечивает генерацию и продвижение заявок по системе. Исполнение такой программы по отношению к конкретной заявке выявляет ее маршрут и времена прохождения этапов маршрута.
- Однако поведение заявки в системе не является независимым, оно обуславливается событиями, в которых фигурируют также другие заявки. Поэтому процесс имитации на ЭВМ должен отображать хронологию событий в последовательности, имеющей место в реальной ВС.
Слайд 40Моделирование
Лекция 3. Организация моделирования СМО
Организация моделирования в СМО:
- Существуют
две проблемы организации моделирования:
1. Процессы в реальной системе зависят от
времени, т.е. необходимо создавать аналог системного времени в модели и соотносить все процессы в зависимости от него.
2. В реальной системе информационные процессы протекают параллельно. В модели это реализовать невозможно, поэтому параллельные процессы надо имитировать как последовательные, обеспечивая при этом все причинно-следственные связи реальной системы.
- Существуют два способа реализации имитационного моделирования:
1. Потактовое моделирование.
2. Событийное моделирование.
Слайд 41Моделирование
Лекция 3. Организация моделирования СМО
Организация моделирования в СМО:
- Потактовое
моделирование.
Расчет всей системы выполняется через некоторый достаточно малый интервал времени
(такт). Выполняется последовательный анализ всех блоков модели в момент времени по известному состоянию в момент времени t.
Новое состояние модели рассчитывается по алгоритмам модели с учетом статистики поведения. На каждом такте моделирования мы обращаемся ко всем моделям и проверяем состояние данной модели в новый момент времени (не изменилось ли оно). Если такт моделирования выбрали слишком большим, то мы можем пропустить какие-либо события, поэтому такт выбирается очень малым.
- Недостатки потактового моделирования:
1. Необходимо выбирать очень маленький шаг.
2. Требуется обращение ко всем моделям, независимо от того, произошли там события или нет (большие вычислительные затраты).
- Достоинство:
1. Простота программной реализации.
Слайд 42Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
- Событийное моделирование за
счет некоторого усложнения алгоритма программы позволяет обойти недостатки потактового моделирования.
-
Для соблюдения при имитации правильной хронологии событий все события, которые в данный момент модельного времени уже известны (можно предвидеть), упорядочиваются по времени наступления этих событий и оформляются в виде списка - списка будущих событий (СБС). Элементами списка являются имена или ссылки на имена заявок, с которыми связаны данные события. Иногда выделяют отдельно начало этого списка, куда относят события, которые должны произойти в текущий момент времени. Этот список называется списком текущих событий (СТС).
Слайд 43Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
- Исполнение программы на
каждом очередном шаге моделирования (новом моменте модельного времени) будет начинаться
с выбора события из СТС и связанной с этим событием заявки, например заявка А.
- Программа должна выполнять все действия с этой заявкой, пока заявка не задержится, например, в очереди или в обслуживающем аппарате.
- После того как программа прерывает имитацию прохождения заявкой А, она переходит к обработке очередного события из СТС. Пусть это событие связано с заявкой В. Программа исполняется, начиная с того оператора, который определил задержку заявки В, и доходит до такого оператора, который означает новую задержку заявки В. Если эта задержка, например из-за обслуживания в некотором устройстве, то при этом определяется длительность обслуживания и, следовательно, момент времени, в который это обслуживание закончится. Далее ссылка на заявку В включается в СБС с указанием времени свершения этого будущего события - окончания обслуживания заявки В в устройстве.
Слайд 44Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
- После этого выбирается
очередной элемент из СТС и имитируется продвижение новой заявки.
- После
того как все события текущего времени ti исчерпываются, модельное время увеличивается до величины ti+1, равной времени ближайшего по времени события, и тогда заявки для момента ti+1 будут новым списком СТС. Процесс имитации продолжается по тому же алгоритму.
- Таким образом, при использовании СБС моделирование выполняется путем обращения к моделям тех элементов ВС, с которыми связаны происходящие события, и выполняется только в те моменты времени, в которые произошли какие-либо события. Такое моделирование, избирательное по месту и времени событий, называется событийным. Достоинством его по сравнению с потактовым моделированием является значительное сокращение вычислительных затрат, так как шаг по времени здесь является оптимальным (от события до события), и обращение происходит на каждом шаге только к тем моделям элементов, в которых произошли события.
Слайд 45Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
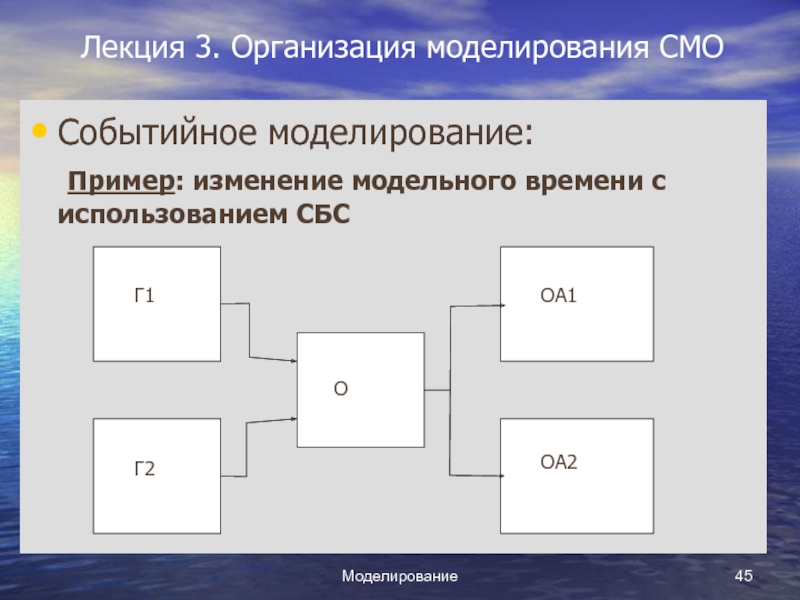
Пример: изменение модельного времени
с использованием СБС
Г1
Г2
О
ОА1
ОА2
Слайд 46Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
Пример: Система содержит два
источника заявок (Г1 и Г2), два обслуживающих аппарата (ОА1 и
ОА2) и общую очередь к ним (О). Кроме событий, непосредственно влияющих на работу системы, в СБС заносятся также моменты времени печати статистических сведений (tпеч.) и др. Список будущих событий для этой системы представим на следующих иллюстрациях, где отражены моменты поступления заявок от Г1 (t1) и от Г2 (t2); моменты выборки заявок из очереди аппаратами ОА1 (Q1) и ОА2 (Q2) (предполагается, что моменты выборки заявок из очереди аппаратами совпадают с моментами времени окончания обслуживания предыдущих заявок в этих аппаратах).
Слайд 47Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
t1
t2
Q1
Q2
tпеч
Г1
Г2
ОА1
ОА2
tm
t
СБС
Слайд 48Моделирование
Лекция 3. Организация моделирования СМО
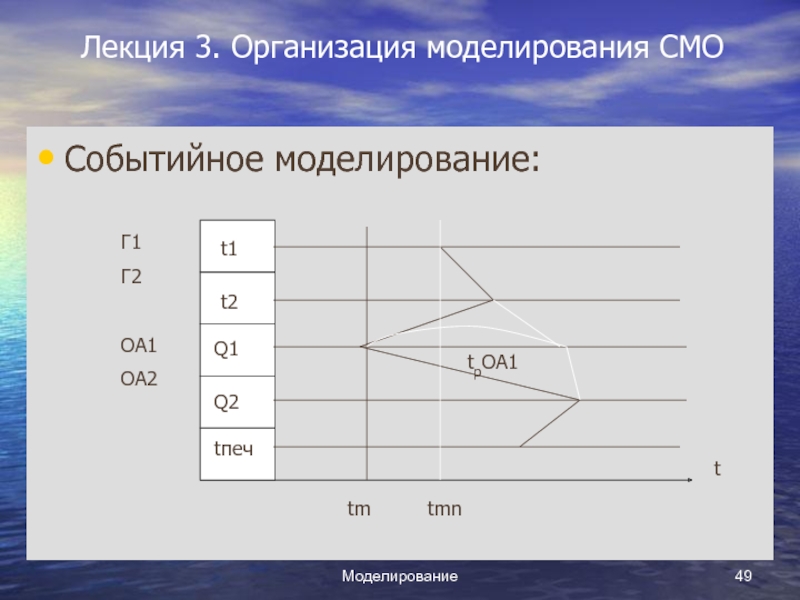
Событийное моделирование:
- Упорядочивание СБС выполняется
визуально.
- Для нашего случая алгоритм моделирования будет выглядеть следующим образом:
1.
выборка из СБС ближайшего события Q1;
2. обращение к подпрограмме (модели) ОА1, связанного с событием Q1;
3. выполнение подпрограммы ОА1. Результатом работы подпрограммы ОА1 будет время обслуживания заявки в данном устройстве (τр.ОА1) и соответственно время выборки из очереди следующей заявки в ОА1;
4. будущее время Q1 становится известным и значение tM + τр. ОА1 заносится в СБС, заменяя старое (предыдущее) значение;
5. очередь уменьшается на одну заявку;
6. СБС упорядочивается, и модельное время увеличивается до ближайшего события из СБС (tMH ).
- Процесс моделирования далее продолжается с выбора очередного ближайшего по времени события (t1, для данного примера).
Слайд 49Моделирование
Лекция 3. Организация моделирования СМО
Событийное моделирование:
t1
t2
Q1
Q2
tпеч
Г1
Г2
ОА1
ОА2
tm
t
tmn
tpОА1
Слайд 50Моделирование
Лекция 3. Организация моделирования СМО
Основные принципы работы имитационного моделирования:
1.
Исходными данными для имитационного моделирования являются:
- Сведения о структуре системы
(состав, связи).
- Сведения о дисциплинах обслуживания в каждом ОА.
- Значения параметров ОА.
- Значения параметров входных потоков заявок.
2. Результатом имитационного моделирования являются следующие рассчитываемые характеристики:
- Пропускная способность (производительность системы) – среднее количество обслуживаемых системой заявок в единицу времени.
- Вероятность обслуживания заявки (для тех систем, где заявки могут покидать систему необслуженными).
- Коэффициенты загрузки оборудования для каждого ОА – отношение полезного времени обслуживания к общему времени моделирования.
- Средние длины очередей к ОА.
Слайд 51Моделирование
Лекция 3. Организация моделирования СМО
Основные принципы работы имитационного моделирования
(продолж.):
3. Имитационная модель представляет собой алгоритм, состоящий из упорядоченных обращений
к моделям элементов. Последовательность обращений определяется свойствами анализируемой ВС и принципами ее функционирования.
4. Модельное время изменяется после того, как закончится имитация событий, относящихся к текущему моменту времени. Имитация заканчивается либо когда текущее время превысит конечное время моделирования, либо когда входные источники выработают необходимое количество заявок.
5. Оценка результатов выполняется на основе принятия решений: по правильности выбранных параметров и структуры ВС, устранению узких мест в системе, изменению дисциплины обслуживания и т.д.
Слайд 52Моделирование
Лекция 3. Организация моделирования СМО
Организация программного обеспечения систем имитационного
моделирования на основе СМО:
- Программная реализация алгоритмов моделирования и языков
описания СМО обычно оформляется в виде пакетов прикладных программ (ППП) сложной структуры.
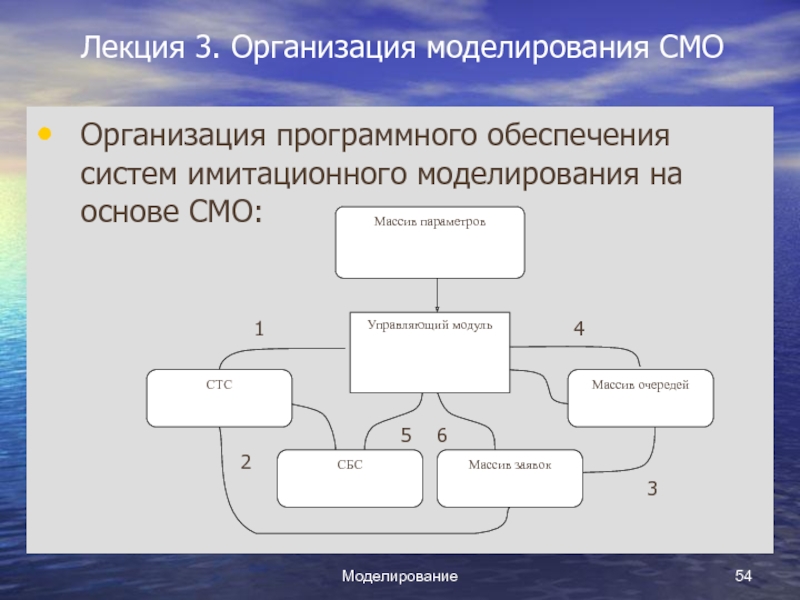
- В состав программного обеспечения входят:
1. Управляющий модуль (управляет обращением к подпрограммам, осуществляет ввод исходных данных, упорядочивает СБС, изменяет модельное время, осуществляет продвижение заявок).
2. Пакеты прикладных подпрограмм (исполнимые модули) – математические модели компонентов, математические модели источников входных потоков, подпрограммы статистической обработки и т.д.
3. База данных системы (СБС, массивы очередей, числовые параметры устройств и заявок).
Слайд 53Моделирование
Лекция 3. Организация моделирования СМО
Организация программного обеспечения систем имитационного
моделирования на основе СМО:
База данных содержит следующие основные массивы данных:
-
Массив очередей содержит информацию о заявках в очереди и упорядочен по устройствам.
- СТС и СБС упорядочены по моментам наступления событий. Их элементы – это ссылки на заявки. По ссылкам могут быть найдены адреса хранения всех сведений о самих заявках.
- Массив заявок хранит сведения о каждой заявке: имя, тип, приоритет и время очередного события, связанного с этой заявкой, место нахождения заявки в модели.
- Массив параметров элементов – числовые параметры законов распределения, дисциплины обслуживания, накапливаемые суммы, длины очередей и вычисляемые характеристики.
Слайд 54Моделирование
Лекция 3. Организация моделирования СМО
Организация программного обеспечения систем имитационного
моделирования на основе СМО:
1
2
3
4
5 6
Слайд 55Моделирование
Лекция 3. Организация моделирования СМО
Организация программного обеспечения систем имитационного
моделирования на основе СМО:
Каждый этап вычислений начинается с выборки очередного
события из СТС (1). Элементом списка является ссылка (2) на заявку (адрес в массиве заявок). Обозначим имя обрабатываемой заявки А. По извлеченным из массива заявок сведениям (3) определяется имя освобождающегося ОА. Если к этому ОА имеется очередь (4), то ОА начинает обслуживать некоторую заявку В из очереди в соответствии с заданной дисциплиной обслуживания. При этом происходит обращение к подпрограмме рассматриваемого ОА, определяется время обслуживания, и тем самым становится предвиденным новое событие – окончание обслуживания заявки В. Ссылка на это событие помещается в список будущих событий (5), и выполняется изменение сведений о заявке В в массиве заявок (6). Далее имитируется продвижение задержанной в очереди заявки А (если нет других заявок в очереди). Это продвижение прерывается, когда производится запрос на обслуживание заявки А в некотором ОА. При этом происходит обращение к массиву очередей по имени этого ОА и либо поступление заявки А на обслуживание, либо постановка ее в очередь. После обработки всех этих действий процесс имитации повторяется, и выбирается очередной элемент из СТС.

Слайд 56Моделирование
Лекция 4. Модели источников входных потоков заявок
Содержание:
Генераторы случайных чисел
Моделирование равномерного
закона распределения
Формирование нормального закона распределения
Распределение Пуассона
Формирование произвольного закона распределения.
Слайд 57Моделирование
Лекция 4. Модели источников входных потоков заявок
Генераторы случайных чисел:
- При
статистическом моделировании одним из основных вопросов является моделирование стохастических воздействий.
Для статистического моделирования характерно большое число операций со случайными числами. Кроме того, результаты статистического моделирования существенно зависят от качества последовательностей случайных чисел. Поэтому наличие простых и экономичных способов формирования случайных чисел требуемого качества во многом определяет возможность моделирования на ЭВМ.
- Существуют три способа генерации случайных чисел (СЧ): аппаратный (физический), табличный (файловый) и алгоритмический (программный).
Слайд 58Моделирование
Лекция 4. Модели источников входных потоков заявок
Генераторы случайных чисел (продолж.):
-
Аппаратный способ - случайные числа вырабатываются специальным электронным устройством –
генератором (датчиком) случайных чисел.
- Достоинствами являются: отсутствие дополнительных вычислительных операций ЭВМ по выработке случайных чисел, необходима только операция обращения к внешнему устройству ЭВМ (датчику), не ограниченный запас чисел, не требуется дополнительная память ЭВМ, высокая скорость работы, генерация "хороших" последовательностей случайных цифр и чисел.
- Недостатками являются: отсутствие гарантии качества последовательности непосредственно во время моделирования системы на ЭВМ (требуются периодические проверки), нельзя повторно получать при моделировании одинаковые последовательности чисел, необходимость дополнительного устройства.
Слайд 59Моделирование
Лекция 4. Модели источников входных потоков заявок
Генераторы случайных чисел (продолж.):
Табличный
способ - случайные числа, оформленные в виде таблицы, помещаются в
виде файла в память ЭВМ. Имеются специальные справочники, где содержатся таблицы случайных чисел, полученные в результате многократного выполнения каких-либо физических опытов. Эта таблица из справочника может быть введена в ЭВМ. Таблицы представляют собой последовательности цифр от 0 до 9, имеющих равную вероятность появления. Использование таких таблиц очень простое: если требуется случайная цифра, то берется первая попавшаяся позиция из таблицы. Если требуется n-позицонное случайное число, то выбирается n последовательных очередных цифр таблицы. Цифры выбираются в любом направлении и с любого места.
Достоинства: генерация действительно случайных чисел, требуется однократная проверка, можно воспроизводить последовательности.
Недостатки: запас чисел ограничен, требуется большой объем памяти ЭВМ.
Слайд 60Моделирование
Лекция 4. Модели источников входных потоков заявок
Генераторы случайных чисел (продолж.):
Алгоритмический
способ - используются специальные алгоритмы и реализующие их программы.
Достоинствами
являются: требуется однократная проверка, можно многократно воспроизводить последовательности чисел, занимает мало место в памяти ЭВМ, не требуется внешнее дополнительное устройство.
Недостатками являются: запас чисел последовательности ограничен ее периодом, более значительные затраты машинного времени.
- Все алгоритмы генераторов СЧ основаны на выборе следующего СЧ как функции от предыдущего, поэтому получаемое СЧ не является полностью случайным, т.к. вычисляется по определенному алгоритму. Такие числа называются псевдослучайными. Эти последовательности очень похожи на действительно случайные числа, а пригодность их применения в процессах моделирования определяется специальными тестами.
Слайд 61Моделирование
Лекция 4. Модели источников входных потоков заявок
Генераторы случайных чисел (продолж.):
В
качестве основных тестов используют проверки на равномерность, стохастичность и независимость.
- Проверка на равномерность осуществляется по гистограмме с использованием косвенных признаков.
- Проверка стохастичности наиболее часто проводится методами комбинаций и серий. Сущность метода комбинаций сводится к определению закона распределения длин участков между единицами (нулями) или закона распределения (появления) числа единиц (нулей) в n-разрядном двоичном числе. Серией называется любой отрезок последовательности случайных чисел, состоящий из следующих друг за другом элементов одного и того же рода. Число элементов в отрезке называется длиной серии.
- Проверка независимости проводится на основе вычисления корреляционного момента. При моделировании с использованием программных генераторов равномерных последовательностей важными характеристиками качества является длина периода P и длина отрезка апериодичности L.
- Длина отрезка апериодичности псевдослучайной последовательности означает, что все числа в пределах отрезка апериодичности не повторяются. Очевидно, что использование при моделировании систем последовательности чисел , длина которой больше отрезка апериодичности L, может привести к повторению испытаний, что не дает новых статистических данных. Из-за того, что разрядная сетка ЭВМ конечна, при формировании последовательности чисел рано или поздно одно из них совпадет с ранее вычисленным числом. После этого все формируемые далее числа будут совпадать с уже имеющимися и при этом будут следовать в том же порядке.

Слайд 62Моделирование
Лекция 4. Модели источников входных потоков заявок
Моделирование равномерного распределения:
Для имитационного
моделирования требуются случайные числа с различными законами распределения – нормальным,
равномерным экспоненциальным и другими. Основой для их генерации является последовательность случайных чисел, распределенных по равномерному закону на интервале (0, 1).
Непрерывная случайная величина имеет равномерное распределение в интервале (а, b), если ее функция плотности имеет вид
Слайд 63Моделирование
Лекция 4. Модели источников входных потоков заявок
Моделирование равномерного распределения:
- На
ЭВМ с n-разрядными числами вместо непрерывной совокупности равномерных случайных чисел
интервала (0, 1) используют дискретную последовательность 2n случайных чисел того же интервала. Закон распределения такой дискретной последовательности называют квазиравномерным распределением.
- Наибольшее применение в практике моделирования нашли алгоритмы вида
xi+1 = F(xi),
представляющие собой рекуррентные соотношения, для которых начальное значение x0 и параметры функции F заданы, например
Xi+1 = λ Xi (mod M),
где λ, Xi , M - неотрицательные целые числа.
- Для реализации на ЭВМ наиболее удобно, когда М = рk , где р - число цифр в системе счисления, принятой в ЭВМ (например, р = 2 для двоичной): k - длина разрядной сетки (например k = 32 для 32-разрядной ЭВМ). В этом случае вычисление остатка от деления на М сводится к выделению k младших разрядов делимого, а преобразование целого числа Xi в рациональную дробь из интервала (0, 1) осуществляется подстановкой слева от Xi двоичной запятой.
Слайд 64Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование нормального закона распределения:
-
Нормальное распределение является одним из важнейших непрерывных распределений. Все методы
базируются на использовании равномерно распределенных случайных чисел.
- Один из часто применяемых метод основан на центральной предельной теореме, которая гласит, что сумма независимых одинаково распределенных случайных чисел с математическим ожиданием am и среднеквадратическим отклонением σm образует асимптотически случайное число с нормальным законом распределения и математическим ожиданием a = N am и среднеквадратическим отклонением σ = σm √ N , где N – число суммируемых чисел. Расчеты показывают, что уже при сравнительно небольших N (8, 12) сумма имеет распределение, близкое к нормальному.
Слайд 65Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование нормального закона распределения:
Нормированное
распределение с M(x) = 0, D(x) = 1 можно получить,
воспользовавшись преобразованием
yнорм = √12/N * (∑ xpавн – N/2).
В частности, при N=12
получим yнорм = ∑ xpавн – 6.
Слайд 66Моделирование
Лекция 4. Модели источников входных потоков заявок
Распределение Пуассона:
- Пусть необходимо
получить случайные числа, имеющие закон распределения Пуассона P(m) = λm
e-λ / m!.
- Для этого распределения можно также воспользоваться предельной теоремой Пуассона, которая гласит, что если при проведении N независимых испытаний вероятность свершения события А в i-ом испытании равна Pi , то относительная частота появления события m/N при N -> ∞ сходится по вероятности к среднему из вероятностей Pi .
- Таким образом, если p – вероятность наступления события А при одном испытании, то вероятность наступления m событий в N независимых испытаниях при N -> ∞, p -> 0, Np = λ асимптотически равна P(m).
- Для реализации алгоритма выбирается достаточно большое N, такое, чтобы p = λ/N < 1, проводятся серии по N независимых испытаний, в каждом из которых событие А происходит с вероятностью p, и подсчитывается число случаев Yj фактического наступления события А в серии с номером j. Числа Yj будут приближенно следовать закону Пуассона, причем тем точнее, чем больше N. Практически N должно выбираться, чтобы p ≤ 0,1 – 0,2. (Алгоритм – в учебнике).

Слайд 67Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование произвольного закона распределения:
Рассмотрим
два метода.
1. Метод обратной функции. Он основывается на следующей теореме:
Если случайная величина (СВ) х имеет плотность распределения Р(х), то
x
j равн = F(x) = ∫ P(x) dx
- ∞
подчиняется равномерному закону распределения в интервале (0, 1) независимо от вида P(x). Отсюда вытекает способ моделирования случайных чисел х с произвольной плотностью вероятности Р(х). Алгоритм: 1) Моделируют СВ ji с равномерным законом распределения в диапазоне (0, 1). 2) Решают интегральное уравнение относительно верхнего предела: хi . Значение верхнего предела хi и будет СВ по закону Р(х). Если Р(х)=0 при х<х0, то вместо ∞ нижний предел можно заменить на х0.
Слайд 68Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование произвольного закона распределения:
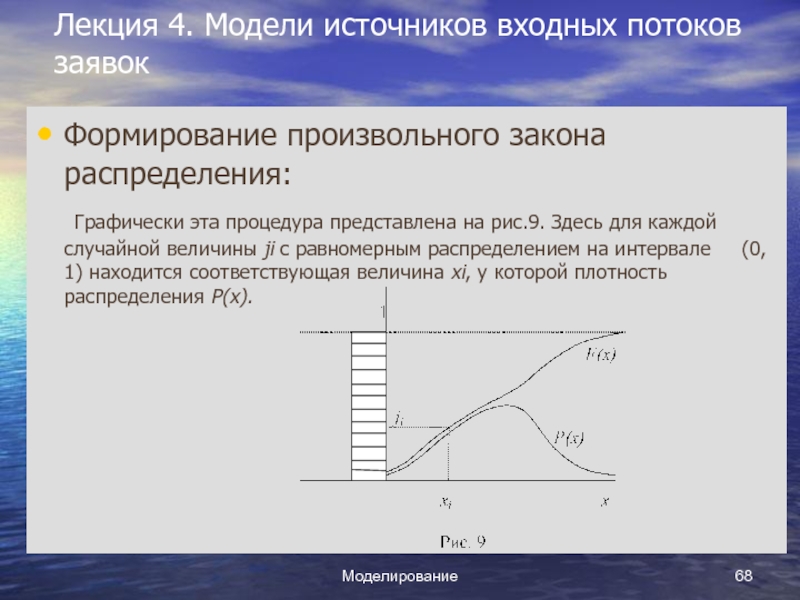
Графически
эта процедура представлена на рис.9. Здесь для каждой случайной величины
ji с равномерным распределением на интервале (0, 1) находится соответствующая величина хi, у которой плотность распределения P(x).
Слайд 69Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование произвольного закона распределения:
Пример
1. Необходимо получить случайные числа с экспоненциальным законом распределения. Для
экспоненциальной случайной величины хi, распределенной по закону
p(x) = a · e-a(x-x0) , xo < x < ∞
имеем xi
ji = ∫ a · e-a(x-x0) dx откуда xi = xo – 1/a · ln (1 - ji )
xo
Пример 2. Необходимо получить случайные числа с законом распределения p(x) = λ(1 – λx/2), 0 < x ≤ 2/λ.
Воспользовавшись приведенным выше алгоритмом, получим
λ(xj – λx²j /4) = yi
Отсюда xj = 2(1 - √(1 - yi ))/λ
или xj = 2(1 - √yi )/λ.
Слайд 70Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование произвольного закона распределения:
Достоинство
метода обратной функции: малые вычислительные затраты при реализации вычисления в
аналитическом виде.
Недостаток: не все законы распределения можно представить в аналитическом виде. Приходится прибегать к численным методам решения, что увеличивает машинное время на получение каждого случайного числа. Даже в тех случаях, когда интеграл берется в аналитическом виде, получаются формулы, содержащие действия логарифмирования, извлечения корня и т.п., которые приводят к увеличению вычислительных затрат.
- Поэтому в практике моделирования часто пользуются другими, более универсальными и иногда приближенными способами.
Слайд 71Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование произвольного закона распределения:
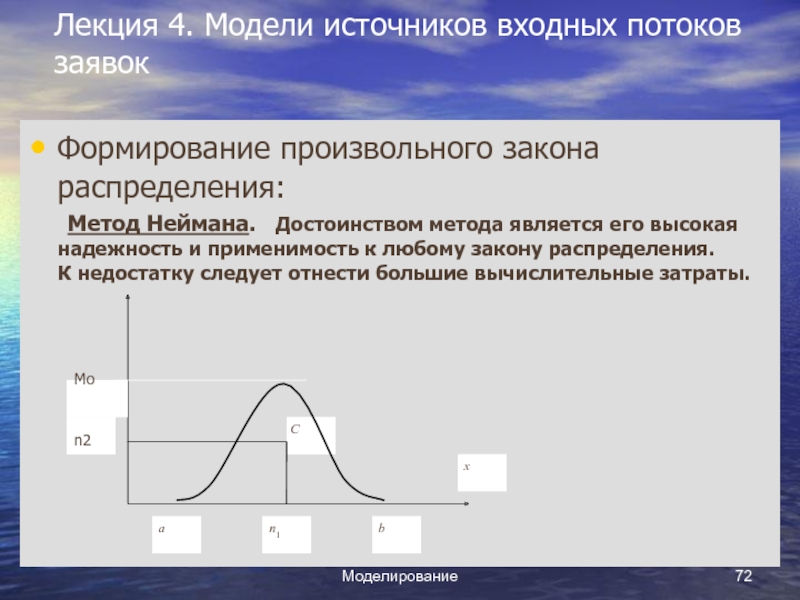
Метод
Неймана.
Если случайная величина х определена на конечном интервале (а,
в) и плотность ее ограничена Р(х) ≤ Мо, то можно использовать следующий алгоритм:
1) Генерируются два значения x1 и x2 случайной величины, равномерно распределенной на интервале (0, 1).
2) Вычисляются координаты точки С(n1;n2):
n1 = a + x1 ·(b - a);
n2 = x2 ·Mo.
3) Если точка С лежит под кривой необходимого закона распределения Р(х), то в качестве очередного СЧ по заданному закону Р(х) выбирают n1, а если над кривой, то пара x1 и x2 отбрасывается и выбирается новая пара.
Слайд 72Моделирование
Лекция 4. Модели источников входных потоков заявок
Формирование произвольного закона распределения:
Метод
Неймана. Достоинством метода является его высокая надежность и применимость
к любому закону распределения. К недостатку следует отнести большие вычислительные затраты.
Mo
n2
Слайд 73Моделирование
Лекция 5. Языки имитационного моделирования
Содержание:
Особенности языков моделирования.
Классификация языков моделирования.
Пример
моделирования ВС.
Слайд 74Моделирование
Лекция 5. Языки имитационного моделирования
Особенности языков моделирования:
- На всех
других уровнях, кроме системного, заданная структура объекта однозначно дает ее
математическую модель, которая получается автоматически по моделям компонентов и топологическим связям.
- Структурные схемы ВС отображают физические связи между устройствами и состав аппаратных средств. Однако реализация тех или иных связей на системном уровне зависит от программного обеспечения, которое на структурной схеме никак не отображается.
- Таким образом, необходимо преобразовывать структуру на каждом шаге ее функционирования так, чтобы отражались только активизированные связи между устройствами, т.е. можно говорить о переменной структуре ВС.
Слайд 75Моделирование
Лекция 5. Языки имитационного моделирования
Особенности языков моделирования:
- Это значительно
усложняет подготовку задания для моделирования на ЭВМ и в отличие
от других уровней делает ее двухэтапной:
- На первом этапе разрабатывается математическая модель ВС, которая обычно не является формальной и выполняется человеком. Большая трудоемкость составления математической модели - главная проблема систем имитационного моделирования. Модель представляется либо в виде схемы, либо в виде алгоритма.
- Второй этап похож на другие уровни моделирования и заключается в представлении результатов первого этапа на языке систем имитационного моделирования.
Слайд 76Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
- Модель ВС
в виде алгоритма - в качестве входных языков системного уровня
очень хорошо подходят алгоритмические языки.
- Но язык моделирования должен отражать определенную структуру понятий для описания широкого класса явлений. Высокий уровень проблемной ориентации языка моделирования значительно упрощает разработку моделей, а специально предусмотренные в ней возможности сбора, обработки и вывода результатов моделирования позволяют быстро и подробно анализировать исходы имитационного эксперимента.
- Основными моментами, характеризующими качество языков моделирования, являются: удобство описания процесса функционирования системы, удобство ввода исходных данных моделирования и варьирования структуры, алгоритмов и параметров модели, возможность реализации статистического моделирования, эффективность выполнения анализа и вывода результатов моделирования, простота отладки и контроля работы моделирующей программы, доступность восприятия и использования языка.
Слайд 77Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
- К настоящему
времени выделяют языки непрерывного и дискретного моделирования, предназначенные для имитации
непрерывных и дискретных процессов.
- Примером языка моделирования непрерывных систем, путем представления моделируемой системы в виде уравнений в конечных разностях является язык DYNAMO. Ряд систем использует прямо системы дифференциальных уравнений, например система MIMIC.
- В рамках дискретного подхода можно выделить несколько групп языков моделирования, различающихся принципами организации процесса моделирования. Это языки, ориентированные на события, процессы и активности (действия, работы). Здесь мы рассмотрим лишь классификацию по способу описания задания на моделирование.
Слайд 78Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
Алгоритмические языки.
Целесообразность
использования алгоритмических языков объясняется тем, что модель ВС представляется в
виде алгоритма. Поэтому известно немало случаев использования алгоритмических языков (Алгол, Фортран и ПЛ/1) при моделировании систем.
Достоинства:
- Необходимо знание только одного языка алгоритмического.
- Необходимо только стандартное ПО.
- Большая гибкость разработки программ, а также отладки и использования модели.
Недостатки:
- Неудобство описаний имитационных моделей.
- Отсутствие лаконичных средств для операций с очередями, управления временем, синхронизации процессов в модели.
- Трудоемкость программирования.
- Сложность внесения изменений.
Слайд 79Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
Расширение алгоритмических языков
(алгоритмические языки, расширенные библиотеками подпрограм для работы с типичными операциями
имитационного моделирования).
Языки SIMSCRIPT, SMPL и FORSIM, созданные на основе алгоритмического языка Фортран. Языки SIMULA и SOL, созданные на основе языка Алгол. Языки СЛЭНГ, НЕДИС, АРГОН – разработаны в нашей стране.
Слайд 80Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
Общецелевые языки имитационного
моделирования.
Характерные черты:
- Специально ориентированы на имитационное моделирование; удобство программирования
модели (что играет существенную роль при разработке крупных систем-моделей).
- Концептуальная направленность на СМО. Язык соответствует определениям и терминам СМО.
- Это не просто высокоуровневые языки - это системы моделирования.
- Представителями этого класса языков являются: GPSS, НЕДИС, СИМУЛА 2, СЛЭНГ, СИМСКРИПТ 2.
- К недостаткам можно отнести:
1. Несколько большие вычислительные затраты при расчетах по имеющимся моделям по сравнению с компиляторами алгоритмических языков.
2. Необходимость сопровождения на ЭВМ дополнительной системы, кроме имеющихся универсальных традиционных компиляторов.
3. Необходимость изучения дополнительного языка, часто с менее кропотливо отработанной документацией, чем в традиционных компиляторах алгоритмических языков.
Слайд 81Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
Специализированные языки.
Целью разработки
этого класса является дальнейшее повышение эффективности имитационного моделирования специально для
ВС. Характерные черты:
- Ориентация не на СМО, а на ВС.
- Включают ПО как часть ВС.
- Служат и для отладки алгоритмов операционных систем ЭВМ.
Недостаток:
В связи с большой специализацией применение этих языков ограничено только задачами моделирования ВС, однако сокращается объем описаний моделей ВС по сравнению с описанием на общецелевых и алгоритмических языках в 4-10 и в 10-80 раз соответственно.
- Представителями данного класса являются языки: МПЛ/ВС, CSS, OASIS.
Слайд 82Моделирование
Лекция 5. Языки имитационного моделирования
Классификация языков моделирования:
Выводы:
1) Создание больших
имитационных моделей, включая разработку алгоритма, кодирование и отладку, требует многих
месяцев работы нескольких отделов высококвалифицированных специалистов. Изменения, вносимые в модель, также приводят к большим затратам времени и средств.
2) Продолжаются работы по созданию новых языков, их упрощению, удобству работы, легкости внесения изменений.
Слайд 83Моделирование
Лекция 5. Языки имитационного моделирования
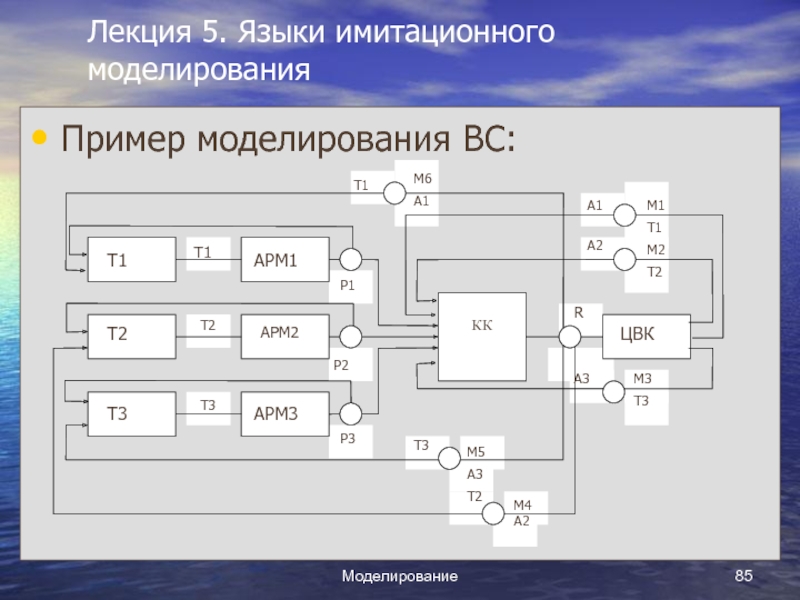
Пример моделирования ВС:
Требуется исследовать процесс
функционирования ВС, состоящей из трех мини-ЭВМ (АРМ1, АРМ2 и АРМ3),
коммутатора канала (КК), осуществляющего сопряжение мини-ЭВМ и ЭВМ центрального вычислительного комплекса (ЦВК) в режиме полудуплексной связи. Требуется оценить загрузку КК, ЦВК и средние времена ожидания обслуживания заявок, поступающих от АРМ.
АРМ1
АРМ2
АРМ3
КК
ЦВК
Слайд 84Моделирование
Лекция 5. Языки имитационного моделирования
Пример моделирования ВС:
1) Первый этап
заключается в подготовке описания модели.
Рассмотрим решение этой задачи на
примере составления схемы сетевой имитационной модели (СИМ).
- Сетевая имитационная модель составляется на основе алгоритма функционирования ВС, который мы представим далее. В СИМ будут представлены те же устройства, что и в структурной схеме, но будут введены дополнительно источники заявок Т1 – Т3 и узлы трех типов:
- Узлы типа Р (Р1, Р2, Р3) - имитируют направление заявок либо к источникам, либо к КК в соответствии с заданными вероятностями.
- Узлы типа R (R1) - имитируют распределение заявок по всевозможным направлениям в зависимости от их типа.
- Узлы типа М (М1, М2, М3, М4, М5, М6) - изменяют тип заявки.
- Источники заявок Т1, Т2 и Т3 имитируют работу операторов в диалоговом режиме с мини-ЭВМ через устройства ввода-вывода, имеющиеся в АРМ.
Слайд 85Моделирование
Лекция 5. Языки имитационного моделирования
Пример моделирования ВС:
Т1
Т2
Т3
АРМ1
АРМ2
АРМ3
ЦВК
Т1
Т2
Т3
Р1
Р2
Р3
Т1
М6
А1
Т3
М5
А3
Т2
М4А2
R
A3
M3
T3
A1
A2
M1
T1
M2
T2
Слайд 86Моделирование
Лекция 5. Языки имитационного моделирования
Пример моделирования ВС:
Исходными данными для
моделирования являются:
- числовые параметры источников входных заявок;
- числовые параметры ОА:
АРМ, КК, ЦВК;
- вероятности решения задач на АРМ.
Алгоритм функционирования:
Работа начинается с генерации каждым источником по одной заявке, которым присваиваются соответственно типы Т1, Т2 и Т3. Тем самым имитируется первое обращение оператора к ЭВМ. Затем эти обращения обрабатываются в АРМ и в зависимости от характера решаемых задач (указываемых в исходных данных) может вызываться обращение к ЦВК или запрос (ответ) оператору. В СИМ эти две альтернативы отображаются узлами Р1, Р2 и Р3, а вероятности задаются в исходных данных. Задачи, направленные в ЦВК, проходят КК, возможно с ожиданием в очереди, а затем через узел R1 поступают в ЦВК, где либо поступают на обслуживание, либо ожидают в очереди. Заявки после освобождения из ЦВК (в виде результатов решения) направляются через КК к оператору, опять возможно с ожиданием в очереди, а чтобы в узле R1 они опять не попали в ЦВК, в узлах М1, М2 и М3 тип заявок изменяется с Т на А. Далее в узлах М4, М5 и М6 восстанавливается исходный тип заявок (Т). Затем, поступившие в АРМ заявки (решения), могут либо выводиться на печать, либо дополнительно обрабатываться на мини-ЭВМ и инициировать генерацию новых заявок Т1, Т2 и Т3.

Слайд 87Моделирование
Лекция 5. Языки имитационного моделирования
Пример моделирования ВС:
2) Второй этап
состоит в описании полученной СИМ средствами входного языка системы моделирования.
Ниже приведен текст описания модели на языке GPSS.
1 GENERATE ,,, 1
2 M1 ASSIGN 1, MM1
3 SEIZE ARM1
4 ADVANCE 2, F2
5 RELEASE ARM1
6 TRANSFER 0.75, M7, M2
7 M2 SEIZE T1
8 ADVANSE 4, F2
9 RELEASE T1
10 TRANSFER .4, M1, M11
11 GENERATE ,,, 1
12 M3 ASSIGN 1, MM3
13 SEIZE ARM2
14 ADVANCE 2, F2
15 RELEASE ARM2
16 TRANSFER 0.75, M7, M4
17 M4 SEIZE T2
18 ADVANSE 4, F2
19 RELEASE T2
20 TRANSFER .4, M3, M11
21 GENERATE ,,, 1
22 M5 ASSIGN 1, MM5
23 …….. ………
Слайд 88Моделирование
Лекция 6. Планирование машинного эксперимента
Содержание:
Планирование эксперимента
Обработка и анализ результатов моделирования
Анализ
и интерпретация результатов моделирования
Слайд 89Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Планирование эксперимента с программной моделью
связано с вопросами эффективного использования ресурсов ЭВМ и определением конкретных
способов проведения испытаний модели. Планирование эксперимента связано прежде всего с решением проблем:
1) определения начальных условий и их влияния на достижение установившегося результата при моделировании;
2) обеспечения точности и достоверности результатов моделирования.
Слайд 90Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Определение начальных условий и их
влияние на результаты моделирования.
- Проблема из-за искусственного характера процесса
функционирования модели, в отличие от реальной системы. Поэтому при очередном прогоне модели требуется определенное время для достижения установившихся режимов работы (занятия устройств и очередей, памятей), соответствующих условиям функционирования реальной системы. Начальный период работы модели искажается из-за влияния начальных условий запуска модели. Существует несколько способов, например:
а) Исключить из рассмотрения информацию о модели, полученную в начальной части периода моделирования, т.е. запоминать и обрабатывать результаты работы модели через достаточно большой период от начала моделирования, который соответствует установившемуся режиму.
б) Задавать такие начальные условия для модели, которые соответствовали бы работе реальной системы.
- Но все имеют недостатки, так в первом случае увеличивается значительно время моделирования, во втором подходе существует проблема - еще до начала моделирования надо знать условия работы реальной системы.

Слайд 91Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Обеспечение точности и достоверности результатов
моделирования.
Эта проблема возникает из-за того, что мы используем вероятностное
моделирование, и никакой машинный эксперимент принципиально не дает точного результата. Инженер всегда решает компромиссную задачу сокращения вычислительных затрат при увеличении точности.
Нет универсальных способов решения этих задач в первую очередь из-за того, что законы распределения в сложных моделях неизвестны. К тому же показатели качества при моделировании не могут быть точно оценены, в лучшем случае можно получить только некоторую оценку такого показателя.
Слайд 92Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Обеспечение точности и достоверности результатов
моделирования.
Пусть Е - показатель качества системы, Е' - оценка
показателя качества системы, в общем случае Е‘ ≠ Е . При этом Е называется точностью (абсолютной) оценки. Вероятность того, что неравенство (Е – Е‘)<ε выполняется, называется достоверностью оценки Q = P {|Е – Е‘|<ε}.
- Основным приемом при решении задач, когда закон распределения в сложных моделях неизвестен, является выдвижение предположений о характере законов распределения случайной величины.
- Рассмотрим пример определения взаимосвязи точности и достоверности результатов моделирования с количеством реализаций N при программном эксперименте, когда в качестве показателя выступает вероятность p .
Слайд 93Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Обеспечение точности и достоверности результатов
моделирования.
Существует две постановки задачи:
1. При заданных величинах точности и
достоверности (ε и Q ) определить необходимое число испытаний N.
2. При заданном N найти ε и Q .
Рассмотрим пример определения взаимосвязи точности и числа испытаний при расчете вероятности р свершения события А, где в качестве оценки вероятности выступает частность ṕ = P(A) = m/N, где m – число свершений события А.
Тогда соотношение, связывающее точность и достоверность оценок с количеством реализаций, будет иметь вид
(3)
Слайд 94Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Обеспечение точности и достоверности результатов
моделирования.
Опуская выкладки по определению математического ожидания и дисперсии, оценки
несмещенности и применения центральной предельной теоремы, можно сделать заключение, что частность m/N при достаточно больших N можно описывать нормальным законом распределения с математическим ожиданием p и дисперсией p(1-p)/N.
Поэтому соотношение (3) с учетом теоремы Лапласа можно переписать как:
где интеграл вероятностей.
Слайд 95Моделирование
Лекция 6. Планирование машинного эксперимента
Обеспечение точности и достоверности результатов моделирования.
Учитывая, что получим
Тогда где - квантиль нормального закона
распределения
порядка , находится из специальных
таблиц. В результате точность оценки можно определить как
т.е. точность оценки обратно пропорционально Количество реализаций определяется соотношением
Слайд 96Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Обеспечение точности и достоверности результатов
моделирования.
Пример: Чтобы оценить, как примерно соотносится число реализаций с
точностью и достоверностью, рассмотрим пример расчета количества реализаций N, когда в качестве показателя эффективности используется вероятность p при достоверности Q = 0,95 (tϕ = 1,96) и точности ε=0,01; 0,02; 0,05.
- Так как значения p до проведения моделирования (эксперимента) неизвестны, то вычислим множество оценок N для диапазона возможных значений p от 0 до 1 с шагом 0,1. Результаты расчетов представлены в табл.
Слайд 97Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента:
Обеспечение точности и достоверности результатов
моделирования.
Слайд 98Моделирование
Лекция 6. Планирование машинного эксперимента
Планирование эксперимента: Обеспечение точности и достоверности результатов
моделирования.
Чаще всего на начальных стадиях моделирования, когда решается вопрос
выбора количества реализаций N, значение p неизвестно. Поэтому на практике выполняют предварительное моделирование для произвольно выбранного значения No, определяют po, а затем по точной формуле вычисляют, используя вместо p значение po необходимое количество реализаций N.
При очень высоких точностях по этим формулам невозможно оценить малые вероятности. Для оценивания малых вероятностей с высокой точностью необходимо очень большое число реализаций. На практике, для оценивания вероятностей порядка p ~ 10-k, количество реализаций выбирают равным N = 10k+1. Очевидно, что даже для сравнительно простых моделей метод статистического моделирования приводит к большим затратам машинного времени.
Слайд 99Моделирование
Лекция 6. Планирование машинного эксперимента
Обработка и анализ результатов моделирования:
При выборе
методов обработки результатов моделирования существенную роль играют две особенности машинного
эксперимента с моделью.
1) Вероятностное моделирование на ЭВМ требует большого числа прогонов модели и хранения большого числа статистических данных. Для решения этой проблемы используют специальные рекуррентные алгоритмы обработки, которые позволяют по ходу моделирования вычислять оценки пользуясь достаточно простыми асимптотическими формулами.
2) Сложность ВС и моделей делает невозможным давать априорно суждение о законах распределения характеристик модели, поэтому при моделировании используются непараметрические оценки и оценки моментов распределения, а не сами распределения.
Слайд 100Моделирование
Лекция 6. Планирование машинного эксперимента
Обработка и анализ результатов моделирования:
Рассмотрим некоторые
удобные для программной реализации методы оценки распределений при достаточно большом
объеме выборки. Математическое ожидание и дисперсия случайной величины ξ соответственно имеют вид
а = m[ξ] = ∫ f(x) ·x dx
δ2 = D[ξ] = m[(x-a)2] = ∫ (x-a)2 ·f(x) ·x dx
Так как плотность распределения априори неизвестна, то определить эти моменты при проведении эксперимента нельзя, поэтому приходится использовать некоторые оценки моментов при конечном числе реализаций N. В качестве таких оценок используются
x̂ = â = 1/N · ∑ xi
S2 = δ2 = 1/N · ∑ (xi –x̂)2
Слайд 101Моделирование
Лекция 6. Планирование машинного эксперимента
Обработка и анализ результатов моделирования:
К качеству
оценок, полученных в результате статистической обработки результатов моделирования, предъявляются следующие
требования:
1) Несмещенность оценки - равенство математического ожидания оценки определяемому параметру m[ĝ] = g, где ĝ - оценка параметра g.
2) Эффективность оценки - минимальность среднего квадрата ошибки данной оценки m[(ĝmin – g)²] ≤ m [(ĝi – g)²], где ĝmin - рассматриваемая оценка, ĝi - любая другая оценка.
3) Состоятельность оценки - сходимость по вероятности при N ->∞ к оцениваемому параметру lim p(|ĝ - g|≥ ε) = 0.
Слайд 102Моделирование
Лекция 6. Планирование машинного эксперимента
Обработка и анализ результатов моделирования:
При реализации
на ЭВМ сложных моделей при большом числе прогонов получается значительный
объем информации. Поэтому необходимо так организовать процесс вычислений и хранения результатов моделирования, чтобы оценки искомых характеристик формировались постепенно по ходу моделирования и без специального запоминания всей информации. Рассмотрим более экономичные формулы вычисления оценок:
а) расчет вероятности наступления события А. В качестве оценки для искомой вероятности p=P(A) используется частота наступления события m/N, где m - число свершений события А; N - общее число исходов. Такая оценка вероятности является состоятельной, несмещенной и эффективной. В памяти ЭВМ достаточно одной ячейки, где накапливается число m, при условии, что N задано заранее;
Слайд 103Моделирование
Лекция 6. Планирование машинного эксперимента
Обработка и анализ результатов моделирования:
б) закон
распределения. Область возможных значений случайной величины разбивается на n интервалов.
Затем накапливается количество попаданий случайной величины в эти интервалы mk . Оценкой для вероятности попадания случайной величины в интервал с номером k служит величина mk /N. Необходимо фиксировать n значений mk , т.е. требуется иметь n ячеек памяти;
в) среднее значение. Накапливается сумма возможных значений случайной величины yk. Тогда среднее значение ŷ =1/N ∑ yk. Требуется всего лишь одна ячейка для накапливаемой суммы.
г) оценка дисперсии. В качестве оценки можно использовать выражение S2 = 1/N · ∑ (yk – ŷ)2 , но непосредственное вычисление по этой формуле нерационально, так как здесь используется среднее значение, которое изменяется в процессе накопления и неизвестно в момент промежуточных вычислений. Более рационально использовать S2 = (∑yk2 - (∑yk )2 /N) /(N-1) и накапливать две суммы.
Слайд 104Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
Решение этой
задачи может быть выполнено различными методами в зависимости от целей
и вида характеристик. Рассмотрим особенности использования двух методов: корреляционного и регрессионного анализа.
Корреляционный анализ используется для определения связи между двумя и более случайными процессами, наблюдаемыми при моделировании. Фактически он сводится к оценке разброса первой случайной величины х относительно среднего значения второй случайной величины ŷ. Существование этих связей можно выразить с помощью коэффициента корреляции:
Слайд 105Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
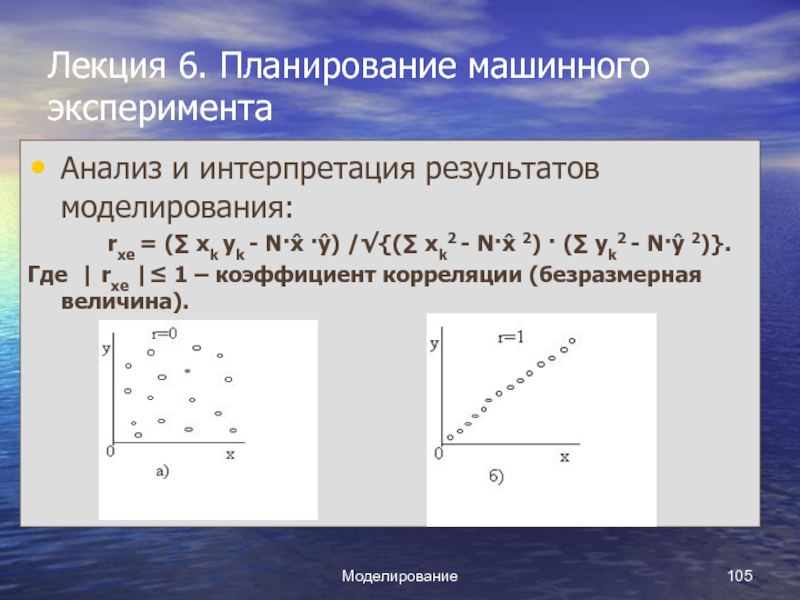
rxe =
(∑ xk yk - N·x̂ ·ŷ) /√{(∑ xk2 - N·x̂
2) · (∑ yk2 - N·ŷ 2)}.
Где | rxe |≤ 1 – коэффициент корреляции (безразмерная величина).
Слайд 106Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
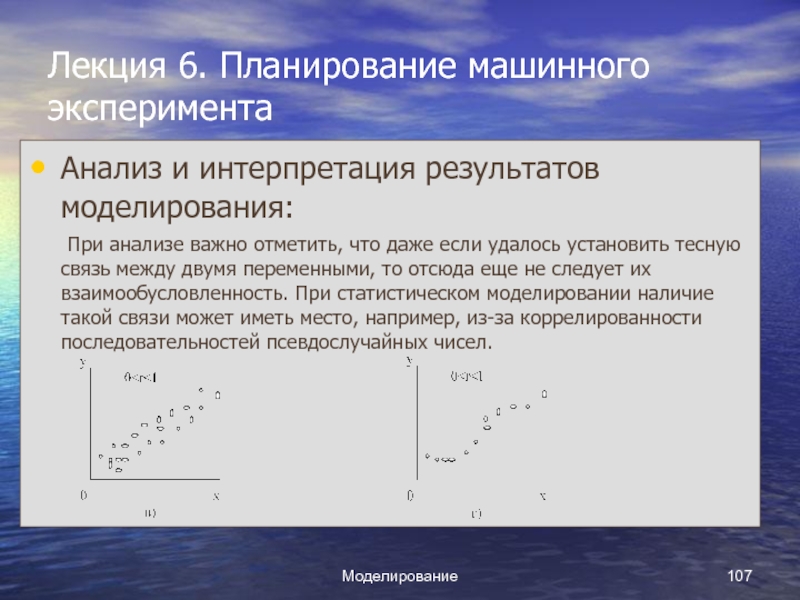
При r
= 0 считается, что статистически два процесса независимы (рис. а).
При |r|=1 считается, что статистически два процесса полностью зависимы - линейная зависимость для рис. б), причем если r>0, то говорят о положительной корреляции, т.е. большие значения одной случайной величины соответствуют большим значениям другой. Случай 0
Слайд 107Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
При анализе
важно отметить, что даже если удалось установить тесную связь между
двумя переменными, то отсюда еще не следует их взаимообусловленность. При статистическом моделировании наличие такой связи может иметь место, например, из-за коррелированности последовательностей псевдослучайных чисел.
Слайд 108Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
Регрессионный анализ
дает возможность построить модель, наилучшим образом соответствующую набору данных, полученных
в ходе машинного эксперимента. В регрессионном анализе минимизируется функция ошибки, являющаяся разностью между моделью и данными эксперимента, а в качестве такой функции берется сумма квадратов ошибок.
- Рассмотрим особенности
регрессионного анализа результатов
моделирования при построении
линейной модели. На рис.
показаны точки полученные в
эксперименте с моделью.
Слайд 109Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
- Далее
предполагается, что модель может быть описана линейным уравнением в виде
прямой линии ŷ = f(x) = b0 + b1 x, где ŷ - величина, получаемая по регрессионной модели.
- Требуется получить такие значения коэффициентов b0 и b1 , при которых сумма квадратов ошибок является минимальной. Ошибки ei для каждой экспериментальной точки определяются как расстояние по вертикали от точки до линии регрессии ŷ = f(x) .
- Выражение для ошибок ei = ŷI – yI = b0 + b1 x, - yI , а функция ошибки
F0 = ∑ (b0 + b1 x, - yI )². Для нахождения b0 и b1 , при которых F0 является минимальной, применяют методы минимизации, например метод наименьших квадратов. Условия: ∂F0 /∂b0 = 0; ∂F0 /∂b1 = 0.
- Дифференцируя, получим:
∂F0 /∂b0 = 2(N b0 + b1 ∑ x, - ∑ yI ) = 0;
∂F0 /∂b1 = 2 b0 ∑ x, + 2 b1 ∑ x,² - 2 ∑ x, yI = 0.
Слайд 110Моделирование
Лекция 6. Планирование машинного эксперимента
Анализ и интерпретация результатов моделирования:
- Решая
систему из двух уравнений, можно получить значения b0 и b1
.
- Аналогично могут быть оценены коэффициенты уравнения регрессии и для случая нелинейной аппроксимации
Слайд 111Моделирование
Лекция 7. Аналитическое моделирование
Содержание:
Основные определения вероятностных событий и потоков
Примеры аналитического
моделирования ВС
Ограничения аналитического моделирования
Слайд 112Моделирование
Лекция 7. Аналитическое моделирование
Основные определения вероятностных событий и потоков:
Потоком событий
называется последовательность событий, происходящих одно за другим в какие-то случайные
моменты времени. Различают потоки однородных и неоднородных событий. Поток событий называется однородным, если он характеризуются только моментами наступления этих событий и задается последовательностью {ti} = {0 < t1 <= t2 . . . .<= ti <= …}, где {ti} – момент наступления i-го события. Однородный поток событий также может быть задан в виде последовательности промежутков времени между двумя соседними событиями {τi}, где
{τi} = ti+1 – ti .
Потоком неоднородных событий называется последовательность, характеризующаяся моментами наступления и набором признаков для этих событий {ti, fi}. В качестве признаков могут быть: принадлежность к тому или иному источнику заявок; наличие приоритета; возможность обслуживания тем или иным ОА.
Слайд 113Моделирование
Лекция 7. Аналитическое моделирование
Основные определения вероятностных событий и потоков:
- Если
{τi} и {τi+1} являются независимыми, то такой поток называется потоком
с ограниченным последействием. Поток называется ординарным, если вероятность того, что в системе находится больше чем одна заявка в момент времени t на интервале dt Р>1 (t, dt), пренебрежимо мала по сравнению с вероятностью того, что в системе находится одна заявка в момент времени t на интервале dt Р1 (t, dt), т.е. Р1 (t, dt) >> Р>1 (t, dt).
- Если для любого интервала dt
Р0 (t, dt) + Р1 (t, dt) + Р>1 (t, dt) = 1,
как сумма вероятностей событий, образующих полную группу, то для ординарного потока событий
Р0 (t, dt) + Р1 (t, dt) = 1, Р>1 (t, dt) = 0.
Слайд 114Моделирование
Лекция 7. Аналитическое моделирование
Основные определения вероятностных событий и потоков:
- Стационарным
называется поток, для которого вероятность появления того или иного числа
событий на интервале τ зависит лишь от длины этого участка τ и не зависит от момента времени, на котором расположен этот участок τ.
- Интенсивностью (плотностью) ординарного потока событий называют предел: lim [Р1 (t, dt) / dt = λ (t).
- Для стационарного потока событий λ (t) = λ = const и означает среднее число событий в системе за единицу времени.
Слайд 115Моделирование
Лекция 7. Аналитическое моделирование
Основные определения вероятностных событий и потоков:
Классификация систем:
-
Системы с потерями - это системы, в которых отсутствуют очереди.
-
Системы с ожиданием - когда все очереди бесконечной емкости.
- Системы смешанные - когда очередь имеет ограниченную длину.
Системы в зависимости от работы с приоритетами делятся на бесприоритетные (приоритеты равны), системы с абсолютным приоритетом и системы с относительным приоритетом. В зависимости от динамики приоритетов различают статические и динамические приоритеты. Статические приоритеты являются фиксированными в пределах решения конкретной задачи моделирования и назначаются заранее. Динамические приоритеты могут менять свои значения при моделировании в зависимости от возникающих ситуаций.
Слайд 116Моделирование
Лекция 7. Аналитическое моделирование
Основные определения вероятностных событий и потоков:
Относительный приоритет
означает, что заявка с более высоким приоритетом ожидает окончания обслуживания
предшествующей заявки и только после этого занимает устройство. Абсолютный приоритет означает, что заявка с более высоким приоритетом при поступлении в очередь прерывает обслуживание заявки с более низким приоритетом и сама занимает устройство (вытесненная заявка может либо покинуть систему, либо поступает опять в очередь, либо занимает устройство сразу после окончания обслуживания заявки с более высоким приоритетом).
Слайд 117Моделирование
Лекция 7. Аналитическое моделирование
Пример аналитического моделирования ВС:
При аналитическом моделировании выделяют
все внутренние параметры системы (x), вектор внешних (Q) параметров (в
качестве него используются параметры входных потоков заявок) и вектор выходных результатов (Y).
Y = f(X, Q).
- Аналитическим моделированием называется представление в виде аналитической зависимости Y как функции от X и Q для системы в целом, а также аналитическое разрешение этого уравнения.
-Пример. Моделирование системы с одним обслуживающим аппаратом и очередью к нему.
- Допустим, что процесс обслуживания начинается при отсутствии заявок в очереди. Тогда состояние СМО описывается следующей системой уравнений:
Слайд 118Моделирование
Лекция 7. Аналитическое моделирование
Пример аналитического моделирования ВС:
Слайд 119Моделирование
Лекция 7. Аналитическое моделирование
Пример аналитического моделирования ВС:
где Pn(t) - вероятность
нахождения в системе n заявок в момент времени t.
-
Модель получена из рассуждений, что вероятность нахождения в системе n заявок в момент времени (t+Δt) равна вероятности нахождения в системе n заявок в момент t, умноженной на вероятность того, что за время Δt в систему не поступит ни одной заявки и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе (n-1) заявок в момент t, умноженная на вероятность того, что за время Δt поступит одна заявка и ни одна заявка не будет обслужена, плюс вероятность нахождения в системе (n+1) заявок в момент t, умноженная на вероятность того, что за время Δt одна заявка покинет систему и не поступит ни одной заявки.
Слайд 120Моделирование
Лекция 7. Аналитическое моделирование
Пример аналитического моделирования ВС:
1) Упростим уравнения, пренебрегая
членами второго порядка малости (Δt)² .Тогда
(1-λΔt) (1-µΔt) ≈ 1-(λ +µ)Δt;
λΔt (1-µΔt) ≈ λΔt;
µΔt (1-λΔt) ≈ µΔt.
После подстановки получим:
Pn (t+ Δt) = Pn (t) [1-(λ +µ)Δt] + Pn-1 (t) λΔt + Pn+1 (t) µΔt, n≥1;
P0 (t+ Δt) = P0 (t) (1-λΔt) + P1 (t) µΔt, n=0.
2) Освобождение от Δt и получение дифференциальных уравнений. Для этого перенесем Pn (t) влево и устремим Δt к нулю. В итоге получим:
dPn(t) / dt = -(λ +µ) Pn(t) + λPn-1(t) + µPn+1(t), n≥1;
dP0(t) / dt = -λP0(t) + µP1(t), n=0.
Слайд 121Моделирование
Лекция 7. Аналитическое моделирование
Пример аналитического моделирования ВС:
3) Решение дифференциального уравнения
можно выполнить для стационарного состояния. Приравняв нулю производные по времени
и исключив таким образом время t из уравнений, получим систему алгебраических уравнений
(λ +µ) Pn = λPn-1 + µPn+1, n≥1;
λP0 = µP1, n=0.
Введем переменную ρ = λ/µ <1.
Тогда (1 + ρ) Pn = ρPn-1 + Pn+1, n≥1;
P1 = ρP0, n=0.
4) Цель нашего решения – найти связь Pn с величинами исходных данных, т.е. ρ. Для этого подставим в первом уравнении n=1. Тогда (1 + ρ) P1 = ρP0 + P2. Подставив сюда P1 из второго уравнения, находим P2 = ρ² P0 . Повторяя эти операции для следующих n=2 и т.д. получим Pn = ρn P0 .
Слайд 122Моделирование
Лекция 7. Аналитическое моделирование
Пример аналитического моделирования ВС:
5) Далее учтем, что
∑Pn =1, так как рассматриваются все возможные состояния (полная группа)
системы. Поэтому ∑ ρn P0 =1, или ∑ ρn P0 = P0 ∑ ρn = P0 /(1-ρ) = 1. Откуда P0 = 1-ρ. Следовательно,
Pn = ρn (1-ρ). Полученное выражение представляет собой геометрическое распределение, для него математическое ожидание числа заявок, находящихся в системе (ОА):
mn = ∑n Pn = (1-ρ) ∑n ρn = ρ (1-ρ). Дисперсия:
Dn = ∑(n - mn)² Pn = ∑n² Pn - [ρ /(1-ρ)]² = mn + mn2 .
Математическое ожидание числа заявок, находящихся в очереди:
Ln = ∑(n - 1) Pn = mn -ρ = ρ /(1-ρ) – ρ = ρ² /(1-ρ) .
Среднее время ожидания заявок в очереди
t̂n = Ln / λ = ρ² /[λ(1-ρ)] .
Слайд 123Моделирование
Лекция 7. Аналитическое моделирование
Применение и ограничения аналитического моделирования:
Аналитическое моделирование применяется
для простых систем и элементов. Возможности аналитического моделирования сильно ограничены,
часто требуется принятие некоторых упрощающих предположений.
- Основные ограничения аналитического моделирования:
1) Входные потоки заявок должны быть стационарными, ординарными и с отсутствием последействия. Такие потоки называют простейшими.
2) Интервалы времени между моментами поступления заявок должны подчиняться экспоненциальному закону распределения.
3) Приоритеты заявок не учитываются.
4) Дисциплина обслуживания должна быть типа FIFO.
5) Времена обслуживания заявок в ОА также подчиняются экспоненциальному закону.
Применения:
1) Для ориентировочных оценок ВС в ряде частных случаев.
2) В качестве макромоделей для отдельных фрагментов ВС при имитационном моделировании.
Слайд 124Моделирование
Лекция 7. Аналитическое моделирование
Пример определения вероятности безотказной работы системы.
- Каждый
блок системы характеризуется собственной вероятностью безотказной работы. Задача состоит в
определении вероятности отказа системы за некоторое время t.
- Вероятность отказа каждого блока равна Qi (t) = ∫ P(t)dt, где P(t) – плотность распределения вероятности отказов.
- Для параллельно соединенных блоков, имеющих
вероятности отказов Q1 (t) и Q2 (t) , суммарная
вероятность отказов определяется как
Qпар (t) = Q1 (t) · Q2 (t) . Для последовательно
соединенных блоков вероятность отказа составит
Qпосл (t) = Q1 (t) + Q2 (t) -
- Q1 (t) · Q2 (t) .
Слайд 125Моделирование
Лекция 8. Сети Петри
Содержание:
Общие сведения о сетях Петри
Примеры сетей Петри
Виды
и свойства сетей Петри
Модель двухуровневой ВС
Слайд 126Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
-Теория сетей Петри,
основанная в начале 60-х годов немецким математиком Карлом Петри (диссертация
1962 года), в настоящее время содержит большое количество моделей, методов и средств анализа и моделирования, и имеет большое количество приложений практически во всех отраслях вычислительной техники и даже вне ее.
- Сети Петри (Petri net) — в первую очередь это математический аппарат для моделирования динамических дискретных систем.
- Сеть Петри кроме математических определений может быть представлена в графическом виде, в виде двудольного ориентированного графа, состоящего из вершин двух типов — позиции (places, места) и переходов (transfer), соединённых между собой дугами.
Слайд 127Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
- Позиции изображаются
окружностями, переходы - отрезками прямой (прямоугольником, утолщенными черточками). Дуги в
сетях Петри - направленные.
Позиции: Переходы:
Входная дуга: Выходная дуга:
- Каждая дуга связывает вершины, только разных классов.
Следующие рисунки иллюстрируют это:
Слайд 128Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
- допустимые примеры
-
недопустимые примеры
Слайд 129Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
- Переходы и
позиции обычно
нумеруются и обозначаются:
переходы – tn, позиции (места)
– pn (sn)
- Математически Сеть Петри
представляется множеством векторов
S = f (P, T, I, O).
где Р - вектор позиций, Т – вектор
переходов, I - вектор входных функций и O - вектор выходных функций.
- В позициях могут размещаться маркеры (метки, фишки, tokens), способные перемещаться по сети. Графически маркировка изображается в виде точек.
- Каждой позиции сети ставится в соответствие натуральное число, указывающее количество фишек в данной позиция.
Слайд 130Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
- Это число
называют разметкой позиции, а совокупность таких чисел для всех позиций
сети называют разметкой (маркировкой) сети. В этом случае сеть называется маркированной. Отсутствие меток в некотором месте говорит о нулевой маркировке этого места.
- Пример маркированной
сети:
Слайд 131Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
- Модель представляет
собой последовательность событий.
- Каждому возможному событию в системе соответствует определенный
переход. Событие будет происходить, если будут удовлетворены определенные условия.
- Каждому условию соответствует определенная позиция. Выполнение условий отображается с помощью маркеров.
- Если позиции пронумерованы (проиндексированы), то состояние системы определяется вектором состояний (или маркировкой), например, Р(0,1,0,0,1,…).
- Каждое изменение маркировки называют событием, т.к. каждое событие связано со срабатыванием определенного перехода.
- Последовательность событий образует моделируемый процесс.
Слайд 132Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Правила срабатывания переходов:
1) Переход срабатывает, если имеются маркеры во всех входных позициях
и число этих маркеров больше чем число дуг, идущих от этих позиций в переход;
2) При срабатывании перехода число маркеров во всех входных позициях уменьшается на число дуг, идущих от этих позиций в переход;
3) Число маркеров увеличивается во всех выходных для данного перехода позициях на количество выходящих из перехода дуг.
Математически правила срабатывания переходов:
- переход срабатывает, если для каждой из его входных позиций
выполняется условие , где — число маркеров в i-й входной позиции, — число дуг, идущих от i-й позиции к переходу; при срабатывании перехода число маркеров в i -й входной позиции уменьшается на , а в j-й выходной позиции увеличивается на , где
— число дуг, связывающих переход с j-й позицией.
Слайд 133Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Иногда в позициях
указывают не метки, а число N, где N означает емкость
данной позиции. В этом случае для дуг, соединяющих позиции и переходы могут быть использованы кратные дуги, где число N называется кратностью дуги, которое графически изображается рядом с дугой. Дуги, имеющие единичную кратность, будут обозначаться без приписывания единицы.
Графическое изображение сети Петри удобно для восприятия и легко преобразуется в исходную программу имитационного моделирования.
Слайд 134Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Пример срабатывания переходов.
В
начальной маркировке позиция S1 имеет две метки, позиция S3 -
одну метку, а позиции S2, S4 - ни одной метки.
Пусть сработают переходы
t1 и t2
Слайд 135Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Получим:
Слайд 136Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Пример: модель простой
ЭВМ.
Требуется описать с помощью сети Петри работу пользователя на ЭВМ
при заданных характеристиках потока запросов и характеристиках поступающих задач.
В модели переходы описывают следующие события:
t12 – (событие) появление задачи на входе ЭВМ,
t10 – (событие) начало решения задачи,
t11 – (событие) окончание решения задачи,
t13 – (событие) выход решенной задачи из ЭВМ.
Позиция Р1 соответствует условию, что во входной очереди имеется задача, Р2 – (условие) решение окончено, Р3 – (условие) процессор свободен, Р4 – (условие) в выходной очереди имеется задача.
Слайд 137Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Начальная маркировка в
данном примере задана исходным вектором
Р0 = (Р1, Р2, Р3, Р4)
= (0, 0, 1, 0).
Приход задачи в ЭВМ отображается запуском перехода t12 и
Появлением маркера в позиции Р1, вектор состояния будет иметь вид
- (1, 0, 1, 0). Теперь удовлетворяются условия для
срабатывания перехода t10, в результате
удаляются маркеры из позиций Р1 и Р3,
помещается маркер в позицию Р2 .
Тогда маркировка будет иметь вид
- (0, 1, 0, 0). Далее выполняются условия
для срабатывания перехода t11,
появляется новая маркировка - (0, 0, 1, 1).
Выполняются условия для срабатывания t13,
и система приходит в исходное состояние
- (0, 0, 1, 0).
P1
t12
t10
P2
P3
t11
P4
t13
Слайд 138Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Переход называется разрешенным,
если каждая из его входных позиций имеет число фишек по
крайней мере равное числу дуг из позиции в переход. Например, если позиции Р1 и Р2 служат входами для перехода t4, тогда t4 разрешен, если P1 и P2 имеют хотя бы по одной фишке:
Слайд 139Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Для перехода
с входным
комплектом
позиция должна обладать по крайней мере тремя фишками, для того чтобы был разрешен:
Слайд 140Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Еще один пример
срабатывания переходов:
В данной сети переходы t0, t2 и t3 разрешены.
Слайд 141Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Маркировка, полученная в
результате запуска перехода t3.
Слайд 142Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Маркировка, полученная в
результате запуска перехода t0. (обратите внимание - из t0 в
p3 идет ДВЕ дуги!!! Поэтому в p3 добавилось ДВЕ фишки).
Слайд 143Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Маркировка, полученная в
результате запуска перехода t2 (и снова обратите внимание на ДВЕ
дуги, идущие из p3 в t2).
Слайд 144Моделирование
Лекция 8. Сети Петри
Общие сведения о сетях Петри:
Моделирование выполняется до
тех пор, пока хотя бы один из переходов будет разрешен.
Поиск тупиковых ситуаций (когда ни один из переходов не является разрешенным) – тема отдельного обсуждения.
В общем случае в позиции может быть
более одного маркера. Рисунок
Иллюстрирует правила срабатывания
переходов при наличии нескольких
маркеров.
Слайд 145Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
Можно вводить ряд дополнительных правил
и условий в алгоритмы моделирования, получая ту или иную разновидность
сетей Петри.
Некоторые виды сетей Петри:
1. Временная сеть Петри
2. Стохастическая сеть Петри
3. Функциональная сеть Петри
4. Цветная сеть Петри
5. Ингибиторная сеть Петри
6. Иерархическая сеть
7. WF-сети
8. Сети с приоритетами.
Слайд 146Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
1. Так, прежде всего полезно
ввести модельное время, чтобы моделировать не только последовательность событий, но
и их привязку ко времени. Это осуществляется приданием переходам веса — продолжительности (задержки) срабатывания, которую можно определять, используя задаваемый при этом алгоритм. Полученную модель называют временной сетью Петри.
Слайд 147Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
Пример. Требуется описать с помощью
сети Петри функционирование системы из предприятий A, В и С.
Предприятия А и В поставляют узлы Х1 и X2 соответственно, а на предприятии С происходит сборка, в каждый сборочный узел входит один узел X1 и два узла X2. На рис. предприятиям А, В и С соответствуют переходы t1, t2 и t3.
Слайд 148Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
Срабатывание перехода t3 происходит только
в том случае, если, во-первых, в позиции pl имеется метка,
а в позиции р2 - не менее двух меток, что означает поступление от предприятии А и В соответствующих комплектующих, и, во-вторых, имеется метка в позиции p4, что означает, что предприятие С закончило сборку предыдущего изделия и готово приступить к сборке следующего. Пока очередное изделие не будет собрано, метки в p4 не будет, следовательно, запросы, пришедшие во входные позиции р1 и р2, вынуждены ожидать срабатывания перехода t4. Переходам t1, t2 и t3 поставлены в соответствие процедуры вычисления задержек срабатывания. Задержки в первых двух переходах равны интервалам времени между появлениями готовых узлов, задержка в t3 равна времени сборки изделия.
Слайд 149Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
2. Если задержки являются случайными
величинами, то сеть называют стохастической сетью Петри. В стохастических сетях
возможно введение вероятностей срабатывания возбужденных переходов. Так, на рис. представлен фрагмент сети Петри, иллюстрирующий конфликтную ситуацию — маркер в позиции Р может запустить либо переход t1, либо переход t2.
В стохастической сети
предусматривается вероятностный
выбор срабатывающего перехода
в таких ситуациях.
Слайд 150Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
Пример. Требуется описать с помощью
сети Петри процессы возникновения и устранения неисправностей в некоторой технической
системе, состоящей из множества однотипных блоков; в запасе имеется один исправный блок; известны статистические данные об интенсивностях возникновения отказов и длительностях таких операций, как поиск неисправностей, замена и ремонт отказавшего блока.
Поиск и замену отказавшего
блока производит одна бригада,
а ремонт замененного блока
— другая бригада. Отметим,
что при числе меток в позиции,
равном M, можно в ней не
ставить M точек, а записать
в позиции значение M.
Слайд 151Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
В нашем примере значение M
в позиции P2 соответствует числу имеющихся в системе блоков. Переходы
отображают следующие события: t1— отказ блока, t2 — поиск неисправного блока, t3 — его замена, t4— окончание ремонта.
Очевидно, что при непустой позиции P2 переход t1 срабатывает, но с задержкой, равной вычисленному случайному значению моделируемого отрезка времени между отказами. После выхода маркера из t1 он попадает через P1 в t2, если имеется метка в позиции P6, это означает, что обслуживающая систему бригада специалистов свободна и может приступить к поиску возникшей неисправности. В переходе t2 метка задерживается на время, равное случайному значению длительности поиска неисправности. Далее маркер оказывается в P3 и, если имеется запасной блок (маркер в P4), то запускается переход t3, из которого маркеры выйдут в P2, P5 и P6 через отрезок времени, требуемый для замены блока. После этого в t4 имитируется восстановление неисправного блока.
Слайд 152Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
3. Если задержки определяются как
функции некоторых аргументов, которыми могут быть количества маркеров в каких-либо
позициях, состояния некоторых переходов и т.п., то имеем функциональную сеть Петри. Функциональная СП характеризуется тем, что отражает не только последовательность событий, но и процессы обработки некоторых потоков данных. Для этого в описание каждого перехода добавляется алгоритм обработки данных.
Слайд 153Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
4. Во многих задачах динамические
объекты могут быть нескольких типов, и для каждого типа нужно
вводить свои алгоритмы поведения в сети. В этом случае каждый маркер должен иметь хотя бы один параметр, обозначающий тип маркера. Такой параметр обычно называют цветом; цвет можно использовать как аргумент в функциональных сетях. Сеть при этом называют цветной сетью Петри.
Понятие цветности в них тесно связано с понятиями переменных, типов данных, условий и других конструкций, более приближенных к языкам программирования. К примеру, цветные сети Петри дополняются введением типов фишек и помогают избежать многократного дублирования фрагментов сети в сложных системах.
Слайд 154Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
5. Среди других разновидностей сетей
Петри следует упомянуть ингибиторные сети Петри, характеризующиеся тем, что в
них возможны запрещающие (ингибиторные) дуги.
Наличие маркера во входной позиции, связанной с переходом ингибиторной дугой, означает запрещение срабатывания перехода.
Слайд 155Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
6. Иерархическая сеть — содержит переходы,
в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого
перехода характеризует выполнение полного жизненного цикла вложенной сети.
Для наглядности такие переходы часто обозначаются большим прямоугольником. Такой переход начинает выполнение с изъятия фишек из входных позиций и завершает, соответственно, помещая фишки в выходные. Основное отличие от простого перехода заключается в том, что между этими двумя моментами могут срабатывать другие переходы.
В момент активации составного перехода из его входных позиций извлекаются фишки, после чего вложенная сеть начинает функционирование исходя из своей начальной разметки. Когда после очередного срабатывания внутреннего перехода вложенной сети в ней не остается разрешенных переходов, она прекращает работу. В этот момент соответствующий составной переход помещает фишки в выходные позиции и переходит в пассивное состояние. При следующей активации составного перехода вложенная сеть снова размечается в соответствии со своей начальной разметкой и начинает новый жизненный цикл.

Слайд 156Моделирование
Лекция 8. Сети Петри
Виды сетей Петри:
7. WF-сети – это подкласс
сетей Петри, называемые также сетями потоков работ, применяют для моделирования
потоков работ в WorkFlow системах.
8. Сети Петри с приоритетами добавляют к разрешенным переходам приоритеты и тем самым позволяют снизить недетерминированность срабатываний, ограничивая множество разрешенных переходов группой переходов с наивысшим приоритетом.
Слайд 157Моделирование
Лекция 8. Сети Петри
Анализ сетей Петри:
- Анализ сложных систем на
базе сетей Петри можно выполнять посредством имитационного моделирования, представленных моделями
сетей Петри. При этом задают входные потоки заявок и определяют соответствующую реакцию системы.
Выходные параметры СМО рассчитывают путем обработки накопленного при моделировании статистического материала.
- Возможен и другой подход к использованию сетей Петри для анализа объектов, исследуемых на системном уровне. Он не связан с имитацией процессов и основан на исследовании системных характеристик и свойств поведения модели, которые характеризуют системные (общие) свойства, не связанные с конкретными внешними воздействиями. Многие такие общие свойства систем могут быть легко получены по СП.
Слайд 158Моделирование
Лекция 8. Сети Петри
Анализ сетей Петри:
Конечные разметки сети
Разметка сети меняется
постоянно. Возможно, что в результате этих изменений некоторый переход потеряет
возможность срабатывать, или наоборот - приобретет ее.
Одна из основных проблем в теории сетей Петри - задача о конечности функционирования сети (системы) (о достижении тупиковой разметки и т.д.).
Суть проблемы состоит в ответе на вопрос для данной конкретной сети - существует ли такая последовательность срабатывания переходов, которая приводит сеть к тупиковой разметке (т.е. разметке, при которой ни один переход не может сработать)?
Слайд 159Моделирование
Лекция 8. Сети Петри
Анализ сетей Петри:
Свойство достижения конечной разметки присуще
далеко не всем сетям.
Например, на рис.4 приведен пример сети всегда
приходящей к
тупиковой разметке,
на рис.5 - сеть никогда
не “попадает в тупик”,
на рис. 6 - сеть, которая
может остановиться, а
может и нет.
Слайд 160Моделирование
Лекция 8. Сети Петри
Анализ сетей Петри:
Другое направление исследования функционирования сети
Петри связано с изменением количества фишек в конкретной или произвольной
позиции в процессе функционирования сети.
Под ограниченностью понимают свойство сети не допускать превышения количества фишек в конкретной или произвольной позиции некоторого
фиксированного числа.
Например, сеть на рис.7
является ограниченной
при любом срабатывании
сети количество фишек
в любой позиции не
превысит 1. На рис.8 нет
тупиков, но не является
ограниченной.
Слайд 161Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
Основными свойствами сети Петри являются:
1.
Ограниченность или K-ограниченность
2. Безопасность
3. Сохраняемость
4. Достижимость
5. Живость
Слайд 162Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
1. Ограниченность (или K-ограниченность) имеет
место, если число меток в любой позиции сети не может
превысить значения К. При проектировании систем определение К позволяет обоснованно выбирать емкости накопителей. Возможность неограниченного роста числа меток свидетельствует об опасности неограниченного роста длин очередей.
Сеть Петри ограничена, если ограничены все ее позиции.
Слайд 163Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
Если известны емкости всех позиций,
и наибольшая из них kmax, то сеть называют kmax-ограниченной.
Ограниченная
сеть
Слайд 164Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
Не ограниченная сеть
Слайд 165Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
2. Безопасность — частный случай
ограниченности, а именно это 1-ограниченность. Если для некоторой позиции установлено,
что она безопасна, то ее можно представлять одним триггером.
Слайд 166Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
3. Сохраняемость характеризуется постоянством загрузки
ресурсов, т.е.
где — число маркеров в
-й позиции, — весовой коэффициент.
Сеть Петри называют
сохраняющей, если
число циркулирующих
в ней объектов
постоянно.
Слайд 167Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
Переход сети Петри называют тупиковым,
если в процессе функционирования сеть может оказаться в состоянии, в
котором этот переход заблокирован. Нетупиковый переход называют активным.
активность уровня 0, если он никогда не может быть активирован (пассивный переход);
активность уровня 1, если существует состояние (достижимое из начального), в котором он активирован;
активность уровня 2, если для всякого целого n существует последовательность срабатывания переходов, в которой данный переход присутствует по крайней мере n раз;
активность уровня 3, если существует бесконечная последовательность срабатывания переходов, в которой данный переход присутствует неограниченно часто;
активность уровня 4, если для любого достижимого состояния существует последовательность срабатываний, приводящая в такое состояние, в котором этот переход активирован (активный переход).
Слайд 168Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
4. Достижимость. Состояние S достижимо
в сети Петри, если существует цепочка срабатываний переходов, ведущая из
начального состояния в S. Состояние S'=(P1'...Pn') покрывает состояние S"=(P1"...Pn"), если для каждого i=1, ...,n имеет место Pi' Pi", т.е. имеет место S' S".
Задача достижимости (покрываемость) состоит в том, чтобы для данной сети и состояния S определить достижимо ли S (достижимо состояние, покрывающее S). Задачи достижимости и покрываемости можно рассматривать применительно к набору не всех, а лишь некоторых позиций, т.е. к подсостояниям сети Петри.
Слайд 169Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
4. Достижимость
характеризуется возможностью
достижения маркировки
из состояния сети, характеризуемого маркировкой .
Достижимость – позволяет определить множество маркировок, в которые возможны переходы в процессе функционирования системы.
Слайд 170Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
5. Живость сети Петри определяется
возможностью срабатывания любого перехода при функционировании моделируемого объекта. Отсутствие живости
означает либо избыточность аппаратуры в проектируемой системе, либо свидетельствует о возможности возникновения зацикливаний, тупиков, блокировок.
Живость – это свойство системы, означающее, что из любого состояния, достижимого из начального, возможен переход в любое другое достижимое состояние.
Слайд 171Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
В основе исследования перечисленных свойств
сетей Петри лежит анализ достижимости.
Один из методов анализа достижимости любой
маркировки из состояния — построение графа достижимости.
Начальная вершина графа отображает , а остальные вершины соответствуют остальным маркировкам. Дуга из в означает событие
и соответствует срабатыванию перехода.
В сложных сетях граф может содержать чрезмерно большое число вершин и дуг. Однако при построении графа можно не отображать все вершины, так как многие из них являются дублями.
Тупики обнаруживаются по отсутствию разрешенных переходов из какой-либо вершины, т.е. по наличию листьев — терминальных вершин. Неограниченный рост числа маркеров в какой-либо позиции свидетельствует о нарушениях ограниченности.
Слайд 172Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
Пример 1
На рисунке вершины графа
изображены в виде маркировок, дуги помечены срабатывающими
переходами. Сеть является
неограниченной и
живой, так
как метки могут накапливаться
в позиции , срабатывают все
переходы, тупики отсутствуют.
Слайд 173Моделирование
Лекция 8. Сети Петри
Свойства сетей Петри:
Пример 2
Сеть, моделирующая
Двухпроцессорную
вычислительную систему
с общей
памятью,
является безопасной,
живой, все разметки
достижимы.
Слайд 174Моделирование
Лекция 8. Сети Петри
Примеры применения сетей Петри:
Защита программ
Сеть Петри является
идеальным инструментом для моделирования переходов при выполнении определенных условий.
Не секрет,
что большинство защит сводится к максимальному сокрытию и недопущения нахождения пресловутого условного перехода. При этом, обертка системы может состоять из самых изощренных анти-отладочных приемов, программа может быть запакована множеством упаковщиков, и любыми другими средствами, но в середине всей этой внешней мишуры находится один единственный переход.
Слайд 175Моделирование
Лекция 8. Сети Петри
Примеры применения сетей Петри:
Защита программ
Допустим, что при
начальной
маркировке можно задавать
кол-во фишек только в позициях
p0…p3. (p7 изначально
содержит
одну фишку). Остальные позиции
недоступны для маркирования.
Зададим ключевому переходу t2
наименьший приоритет, после
чего он (переход t2) выполниться
тогда и только тогда, когда
начальная маркировка будет
в p0…p3 следующим образом:
p0=1, p1=0, p2=1, p3=1. При всех остальных начальных маркировках
переход t2 не сработает. Попытайтесь проверить.
Слайд 176Моделирование
Лекция 8. Сети Петри
Примеры применения сетей Петри:
Защита программ
Теперь представим, что
каждый переход – это поток, который проверяет определенный набор бит
на ВХОДЕ (входные позиции) и в зависимости от результата устанавливает биты на ВЫХОДЕ. Так, поток t3 проверяет фишки (биты) в позиции p0 и в зависимости от того есть там фишки (бит установлен) или нет (бит сброшен) устанавливает биты на выходных позициях (p5 и p6).
Допустим, пользователю необходимо зарегистрировать программу, введя 4-битный ключ. Биты ключа (фишки) помещаются в позиции p0,p1,p2 и p3. Этим обеспечивается начальная маркировка сети.
Программа будет считаться зарегистрированной, если переход t2 сработает (т.е. будет активным). Как уже было показано выше – переход t2 сработает только при такой начальной маркировке: p0=1, p1=0, p2=1, p3=1.
Все это легко можно реализовать программно.
Слайд 177Моделирование
Лекция 8. Сети Петри
Примеры применения сетей Петри:
Защита программ
Решая задачу достижимости
с использованием дерева достижимости мы фактически прибегаем к методу полного
перебора. К данному методу вообще можно свести любую задачу. Поэтому защищенность здесь определяется только временем и ресурсами, затраченными на полный перебор.
На нашем примере легко видеть, что найти правильный ключ (т.е. правильную начальную маркировку) можно перебрав всего лишь 2^4 = 16 значений. Это можно сделать даже вручную, а взглянув на представление программы в виде сети Петри можно догадаться интуитивно за несколько секунд.
Использование ключей длиной менее 2^128 бит на сегодняшний день не может обеспечить защиту на приличном уровне, именно поэтому предложенная в примере сеть Петри не годится для практической защиты и приведена лишь в качестве наглядной иллюстрации.
Слайд 178Моделирование
Лекция 8. Сети Петри
Пример моделирования двухуровневой ВС:
- Рассмотрим моделирование ВС,
которую исследовали на языке GPSS при условии, что отсутствует КК
и модель отражает работу только одного АРМ.
- Это временная стохастическая сеть.
- Считаются заданными параметры распределения случайной величины: время реакции пользователя на результаты обработки очередной порции информации; время обработки порции информации в АРМ и ЦВК; вероятность направления задания в ЦВК (q1); вероятность окончания решения (q2) после обработки очередной порции.
Слайд 179Моделирование
Лекция 8. Сети Петри
Пример моделирования двухуровневой ВС:
1-q
t7
Слайд 180Моделирование
Лекция 8. Сети Петри
Пример моделирования двухуровневой ВС:
- Позиции Р1 и
Р2 и переходы t1 и t2 отражают поведение источника входных
потоков заявок, имитирующего поступление запросов на использование АРМ.
- Позиции Р3 и Р4 и переходы t3 и t4 соответствуют работе пользователя за дисплеем АРМ.
- Позиции Р5 и Р6 и переходы t5 и t6 соответствуют работе АРМ (обработка информации).
- Из Р6 заявки с вероятностью q1 поступают на t6 и с вероятностью (1 - q1) поступают на t4. Переход t 5 регулирует задержку в АРМ.
- Позиция Р7 и переход t7 отображают направление задач с вероятностью (1 - q2) на решение в ЦВК. Позиции Р8, Р9, Р10 и переходы t8, t9 отображают обработку информации в ЦВК. Выход задач из системы происходит через переход t10.
Слайд 181Моделирование
Лекция 9. Цепи Маркова
Содержание:
Основные определения
Примеры
Применение
Слайд 182Моделирование
Лекция 9. Цепи Маркова
Основные определения:
- Цепь Маркова (Markov Chain) —
последовательность случайных событий, характеризующаяся тем свойством, что при фиксированном настоящем
будущее независимо от прошлого.
- Марков Андрей Андреевич, 1856—1922.
- Родился в Рязанской губернии.
- В 1878 окончил Петербургский университет. С 1880 — приват-доцент, с 1886 — профессор, а с 1905 — заслуженный профессор Петербургского университета, с 1896 — ординарный академик Императорской Санкт-Петербургской Академии Наук.
Слайд 183Моделирование
Лекция 9. Цепи Маркова
Основные определения:
1. Процесс, протекающий в физической системе,
называется марковским, если в любой момент времени вероятность любого состояния
системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние.
2. Цепью Маркова называется последовательность испытаний, в каждом из которых появляется только одно из k несовместных событий Ai из полной группы. При этом условная вероятность pij(s) того, что в s–ом испытании наступит событие Aj при условии, что в (s–1)–ом испытании наступило событие Ai, не зависит от результатов предшествующих испытаний.
Слайд 184Моделирование
Лекция 9. Цепи Маркова
Основные определения:
3. События называются состояниями системы, а
испытания – изменениями состояний системы.
Пусть вероятность
того, что в результате n шагов (испытаний) система перейдет из состояния в состояние . Например, – вероятность перехода за 10 шагов из третьего состояния в шестое. Отметим, что при n=1 эта вероятность сводится просто к переходной вероятности .
4. Допустим, число состояний конечно и равно k.
Тогда матрица, составленная
из условных вероятностей
перехода будет иметь вид:
Слайд 185Моделирование
Лекция 9. Цепи Маркова
Основные определения:
5. Эта матрица называется матрицей перехода
системы. Т.к. в каждой строке содержаться вероятности событий, которые образуют
полную группу, то сумма элементов каждой строки матрицы равна единице.
Слайд 186Моделирование
Лекция 9. Цепи Маркова
Основные определения:
6. Равенство Маркова. Вопрос: как, зная
переходные вероятности , найти вероятности перехода состояния
i в состояние j за n шагов. Рассмотрим промежуточное (между i и j ) состояние r. Из первоначального состояния i за m шагов система перейдет в промежуточное состояние r с вероятностью
, после чего за оставшиеся n–m шагов из промежуточного состояния r она перейдет в конечное состояние j с вероятностью . По формуле полной вероятности, получим:
Эту формулу называют равенством Маркова.
Слайд 187Моделирование
Лекция 9. Цепи Маркова
Основные определения:
- Зная матрицу перехода
за один шаг, т.е. можно найти
вероятности перехода за два шага , а значит, и саму матрицу перехода , далее – по известной матрице – найти и т.д.
- Полагая в равенстве Маркова n=2, m=1 получим:
или .
- В матричном виде это можно записать, как .
- Полагая n=3, m=2, получим . В общем случае справедливо соотношение
Слайд 188Моделирование
Лекция 9. Цепи Маркова
Основные определения:
- Пример. Пусть матрица перехода равна
.
- Требуется найти матрицу перехода
.
- Умножая матрицу саму на себя, получим
-На основе матрицы перехода системы можно построить граф состояний системы. Удобно для наглядного представления цепи.
Слайд 189Моделирование
Лекция 9. Цепи Маркова
Примеры
1. Если заданы начальное распределение вероятностей и
матрица перехода, то вероятности состояний системы на n-м шаге вычисляются
по рекуррентной формуле (частный случай равенства Маркова):
Рассмотрим пример (функционирование прибора). Пусть прибор в течение одних суток может находиться в одном из двух состояний – исправном (S1) и неисправном (S2 ). В результате массовых наблюдений за работой прибора составлена следующая матрица перехода:
Слайд 190Моделирование
Лекция 9. Цепи Маркова
Примеры
где P11 – вероятность того, что прибор
останется в исправном состоянии;
P12 – вероятность перехода прибора из исправного
в неисправное состояние;
P21 – вероятность перехода прибора из неисправного в исправное состояние;
P22 – вероятность того, что прибор останется в состоянии «неисправен».
Пусть вектор начальных вероятностей
состояний прибора задан соотношением , т.е.
(в начальный момент прибор был неисправен). Требуется определить вероятности состояния прибора через трое суток.
Слайд 191Моделирование
Лекция 9. Цепи Маркова
Примеры
Решение: Используя матрицу перехода, определим вероятности состояний
после первого шага (после первых суток):
.
Вероятности состояний после второго шага (вторых суток) равны:
Вероятности состояний после третьего шага (третьих суток) равны:
Таким образом, вероятность того, что прибор будет находиться в исправном состоянии равна 0,819, и того, что в неисправном – соответственно 0,181.
Слайд 192Моделирование
Лекция 9. Цепи Маркова
Применение
1. Определение авторства текста
- Частоты употребления пар
букв очень хорошо характеризуют автора.
- Первые пробные шаги предпринял
еще А.А. Марков. Изучал распределение доли гласных и согласных среди первых 20000 букв "Евгения Онегина".
- На основании исследований параметров авторского стиля на огромном числе произведений писателей XVIII-XX веков, доказано, что доля всех служебных слов в длинном прозаическом произведении является т.н. авторским инвариантом.
- Метод основывается на цепи Маркова. По известным произведениям автора вычисляется матрица переходных частот употреблений пар букв.
- Для каждого автора оценивается вероятность того, что именно он написал анонимный фрагмент текста. Автором анонимного текста полагается тот, у которого вычисленная оценка вероятности больше.
Слайд 193Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
- При поиске
и ранжировании документов Google основывается на содержании страницы, ключевых словах
в заголовке, описании и на значении PageRank.
- PageRank - число, отображающее важность страницы.
- Для расчета PageRank используется следующая формула:
PR(A) = (1-d) + d∙ ( PR(T1)/C(T1) + … + PR(TN)/C(TN))
где PR(A) – PageRank страницы А; T1… Tn – страницы, ссылающиеся на А; C(T1) – количество ссылок страницы T1; d – коэффициент затухания, находится в пределах от 0 до 1, обычно равен 0,85.
- Ограничение: ∑PRj = N, j=1…N, N – количество страниц в сети.
Слайд 194Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
Пример, сеть из
четырех страниц
На первом шаге (итерации) расчет (при условии, что PageRank
всех страниц равен 1) дает
PR(A) = (1-0,85) + 0,85∙ ( PR(B)/1 + PR(C)/1) = 0,15 + 0,85∙ ( 1/1 + 1/1) = 1,85.
PR(B) = (1-0,85) + 0,85∙ ( PR(A)/3 + PR(D)/1) = 0,15 + 0,85∙ ( 1/3 + 1/1) = 1,28.
PR(C) = (1-0,85) + 0,85∙ ( PR(A)/3) = 0,15 + 0,85∙ ( 1/3) = 0,43.
PR(D) = (1-0,85) + 0,85∙ ( PR(A)/3) = 0,15 + 0,85∙ ( 1/3) = 0,43.
Слайд 195Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
На втором этапе,
подставляем не 1, а полученные значения:
PR(A) = 0,15 + 0,85∙
(1,28/1 + 0,43/1) = 1,609.
PR(B) = 0,15 + 0,85∙ (1,85/3 + 0,43/1) = 1,425.
PR(C) = 0,15 + 0,85∙ ( 1,85/3) = 0,674.
PR(D) = 0,15 + 0,85∙ ( 1,85/3) = 0,674.
После 10 шагов - сходимость, результат:
PR(A) = 1,637;
PR(B) = 1,136;
PR(C) = 0,614;
PR(D) = 0,614.
Сумма всех PR равна 4, ограничение выполняется.
Слайд 196Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
Страница A имеет
самый высокий PR, страницы С и D – наиболее низкий,
т.е. вероятность попасть на страницу A больше всего.
Поэтому если все четыре страницы, будут по содержанию соответствовать какому-то запросу поиска, то несмотря на достаточно похожее содержание страниц, после учета значений PR, страница A окажется на первом месте, B – на втором, а C и D – на третьем.
Данный процесс является Марковским.
Обозначим шаги (этапы) процесса за t = 0, 1,…..
Формула расчета в матричном виде выглядит следующим образом:
P(t+1) = P(t) ∙P. Отсюда следует, что P(t) = P(0) ∙Pt и P(*)=P(*)∙P - предельный вектор вероятностей P(*), является единственным и не зависит от вектора начальных вероятностей P(0) и определяются только матрицей вероятностей перехода.
Слайд 197Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
Матрица вероятностей перехода:
Первая
строка - со страницы A можно перейти на B, C,
и D. Вероятность того, что после A пользователь выберет В равна 1/3. Вероятность выбора D или C тоже равна 1/3.
Вторая строка - со страницы B можно попасть только на A, вероятность этого перехода равна 1. Третья строка – с C можно попасть только на A, вероятность перехода равна 1. Четвертая строка – с D можно попасть только на B, вероятность перехода равна 1.
Слайд 198Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
Вектор начальных вероятностей
(т.к. четыре страницы и пользователь может оказаться на любой из
них с одинаковой вероятностью):
P(0) = < 1/4, 1/4, 1/4, 1/4>.
Для расчета вектора P(1), P(0) умножим на матрицу вероятностей перехода. Получим P(1) = <0,5; 0,3333; 0,0833; 0,0833>.
Для вектора P(2): P(2) = P(1) ∙P. После расчета получаем значения P(2) = <0,4167; 0,25; 0,167; 0,167>.
Значение предельного вектора вероятностей P(*), который не зависит от вектора начальных вероятностей P(0) и определяется только матрицей вероятностей перехода.
В нашем случае P(*) = <0,429; 0,286; 0,143; 0,143>.
42% пользователей будут на странице A, 29% будут на странице B и на страницах C и D будет по 14% посетителей.
Слайд 199Моделирование
Лекция 9. Цепи Маркова
Применение
2. Поисковые системы. Применение PageRank
Теперь с полученным
вектором P(*) произведем следующие действия: 0.85∙4P(*) + (1-0,85)
Проведем расчеты:
Для А:
0,85∙4∙0,429 + 0,15 = 1,607.
Для B: 0,85∙4∙0,286 + 0,15 = 1,12.
Для C: 0,85∙4∙0,143 + 0,15 = 0,635.
Для D: 0,85∙4∙0,143 + 0,15 = 0,635.
Получается что, рассчитав предельный вектор вероятностей P(*), умножив его на единичный вектор, умноженный на 4d, и прибавив к нему единичный вектор, умноженный на (1-d), мы получили значения практически равные значениям PR, рассчитанным ранее.
Слайд 200Моделирование
Лекция 9. Цепи Маркова
Применение
3. Автоматическое формирование текста и спама
- Рассмотрим
текст, состоящий из слов W.
- Представим процесс, в котором
состояниями являются слова, так что когда он находится в состоянии (Si) система переходит в состояние (Sj) согласно матрице переходных вероятностей.
- Сначала «обучают» систему: на каком-то тексте оценивают переходные вероятности.
- Затем на основе матрицы строят текст.
- Увеличение смысла в тексте, построенном при помощи алгоритма цепей Маркова возможно только при увеличении порядка, где состоянием является не одно слово, а множества — пары (U, V), тройки (U, V, W) и т.д.
- Причем смысл начнет появляться при увеличении размерности порядка как минимум до среднего количества слов в типовой фразе исходного текста.
Слайд 201Моделирование
Лекция 9. Цепи Маркова
Применение
3. Автоматическое формирование текста и спама
- В
Интернете для создания web-контента и поискового спама.
- Увеличить трафик
на свой сайт и повысить его рейтинг в поисковых системах, можно помещая на свои страницы как можно больше ключевых слов для поиска. Для этого используют тексты, созданные генератором на основе марковской цепи.
4. Другие
- Расчет сумм для обязательного страхования автогражданской ответственности
- Расчет результатов лотерей и т.п.
Литература
1. Беляев А., Гаврилов М., Масальских А., Медвинский М. Марковские процессы, 2004.
2. Алексеев В. Марковские процессы принятия решений, 2002.
3. Беляев А. Марковские цепи, 2002.