Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование селевых потоков с помощью компьютерных программ
Содержание
- 1. Моделирование селевых потоков с помощью компьютерных программ
- 2. ПланВведениеИнформация о селевых потокахПонятие математической модели селевого
- 3. ВведениеДля предупреждения селей и осуществления защитных мероприятий
- 4. Информация о селевых потоках Сели — временные
- 5. Понятие математической модели селевого процесса Математическая
- 6. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СЕЛЕВЫХ И СКЛОНОВЫХ ПРОЦЕССОВТип: непрерывные
- 7. Математическая модель DEBRISМодель”DEBRIS”—цифровая модель взаимодействия элементарных сферических
- 8. Математическая модель Божинского-Назарова Модель
- 9. Математическая модель RAMMS Модель RAMMS позволяет моделировать
- 10. Моделирование селя в Кабардино-БалкарииПродольное сечение реки Герхожан-Су
- 11. В модели DEBRIS реализация схода селевого потока
- 12. Моделирование Уаскаранской ледниковой катастрофыИсходными данными для моделирования
- 13. ЗаключениеУниверсальной математической модели, которая могла бы в
- 14. ЛитератураБожинский А. Н., Назаров А. Н. Динамика
- 15. СПАСИБО ЗА ВНИМАНИЕ!
- 16. Скачать презентанцию
ПланВведениеИнформация о селевых потокахПонятие математической модели селевого процесса. Классификация моделейМатематическая модель DEBRISМатематическая модель Божинского-НазароваМатематическая модель RAMMSМоделирование селя в Кабардино-Балкарии с помощью модели Божинского-Назарова и модели DEBRISМоделирование Уаскаранской ледниковой катастрофы с помощью
Слайды и текст этой презентации
Слайд 1Моделирование селевых потоков с помощью компьютерных программ
Ночуйкина Анастасия
студентка 2 курса
специальность
«Строительство уникальных зданий и сооружений»
Н. В.Слайд 2План
Введение
Информация о селевых потоках
Понятие математической модели селевого процесса. Классификация моделей
Математическая
модель DEBRIS
Математическая модель Божинского-Назарова
Математическая модель RAMMS
Моделирование селя в Кабардино-Балкарии с
помощью модели Божинского-Назарова и модели DEBRISМоделирование Уаскаранской ледниковой катастрофы с помощью модели RAMMS
Заключение
Литература
Слайд 3Введение
Для предупреждения селей и осуществления защитных мероприятий необходимы комплексные исследования,
в том числе математическое моделирование с помощью компьютерных программ.
Слайд 4Информация о селевых потоках
Сели — временные потоки, образующиеся в
оврагах, на крутых горных склонах, а нередко и в долинах
горных рек.Слайд 5
Понятие математической модели селевого процесса
Математическая модель селевого процесса — эквивалент
селевого процесса, отражающий в математической форме характерные свойства данного процесса
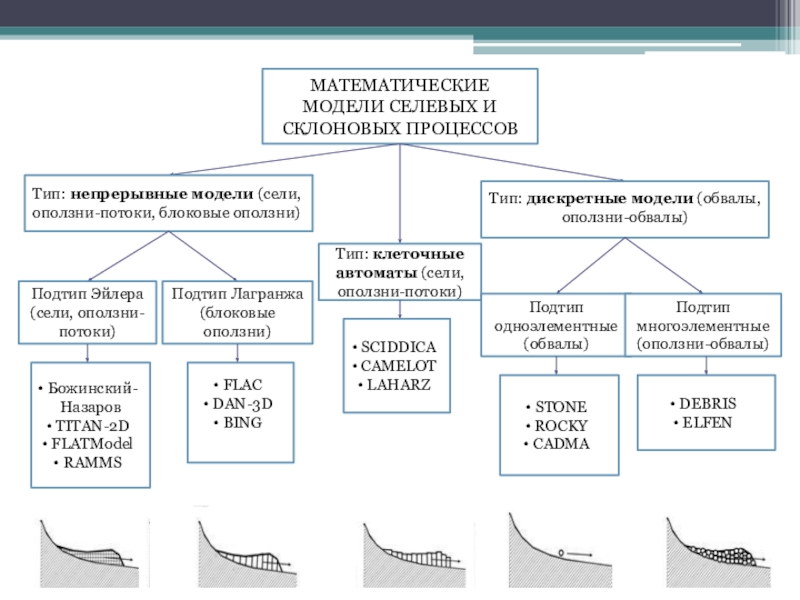
— законы физики, которым он подчиняется, а также его внутреннюю структуру.Слайд 6МАТЕМАТИЧЕСКИЕ МОДЕЛИ СЕЛЕВЫХ И СКЛОНОВЫХ ПРОЦЕССОВ
Тип: непрерывные модели (сели, оползни-потоки,
блоковые оползни)
Тип: дискретные модели (обвалы,
оползни-обвалы)
Тип: клеточные автоматы (сели, оползни-потоки)
Подтип
Эйлера (сели, оползни-потоки)Подтип Лагранжа (блоковые оползни)
Подтип одноэлементные (обвалы)
Подтип многоэлементные (оползни-обвалы)
SCIDDICA
CAMELOT
LAHARZ
Божинский-Назаров
TITAN-2D
FLATModel
RAMMS
FLAC
DAN-3D
BING
STONE
ROCKY
CADMA
DEBRIS
ELFEN
Слайд 7Математическая модель DEBRIS
Модель”DEBRIS”—цифровая модель взаимодействия элементарных сферических частиц и поверхности,
создана В.О. Михайловым. Движение селевого потока в ней имитируется движением
потока горошин в лотке, который по форме соответствует рельефу выбранной территории.Слайд 8
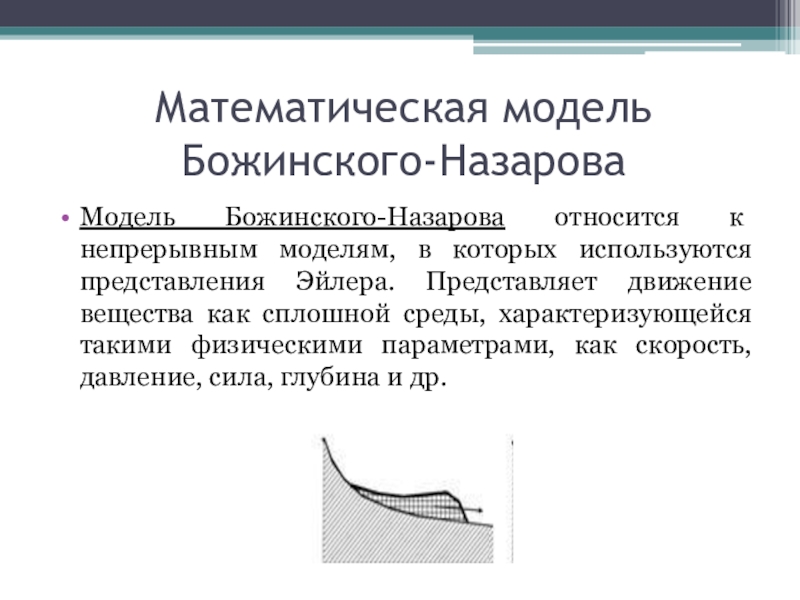
Математическая модель
Божинского-Назарова
Модель Божинского-Назарова относится к непрерывным моделям, в которых
используются представления Эйлера. Представляет движение вещества как сплошной среды, характеризующейся
такими физическими параметрами, как скорость, давление, сила, глубина и др.Слайд 9Математическая модель RAMMS
Модель RAMMS позволяет моделировать движение лавинного потока в
условиях трехмерного рельефа. Разработана Швейцарским институтом снеголавинных исследований. Снежные лавины
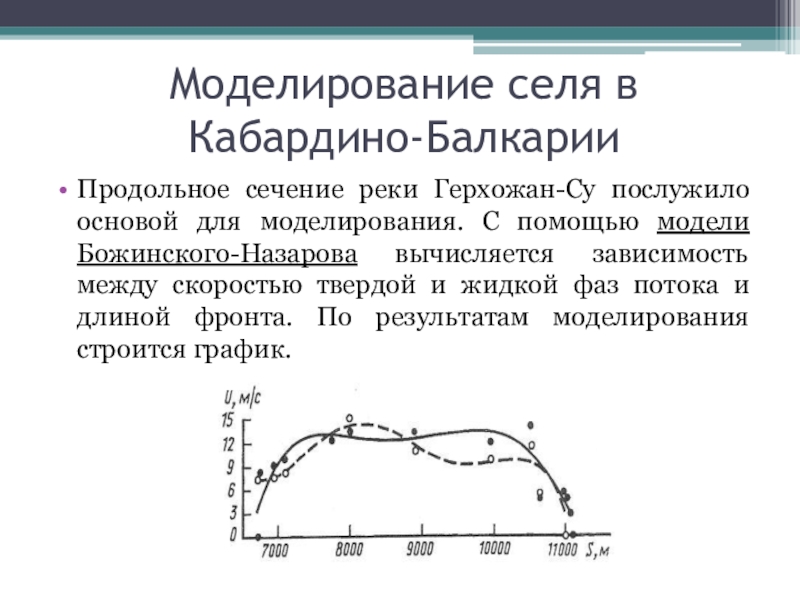
моделируются в RAMMS как несжимаемая сплошная среда средней постоянной плотности.Слайд 10Моделирование селя в Кабардино-Балкарии
Продольное сечение реки Герхожан-Су послужило основой для
моделирования. С помощью модели Божинского-Назарова вычисляется зависимость между скоростью твердой
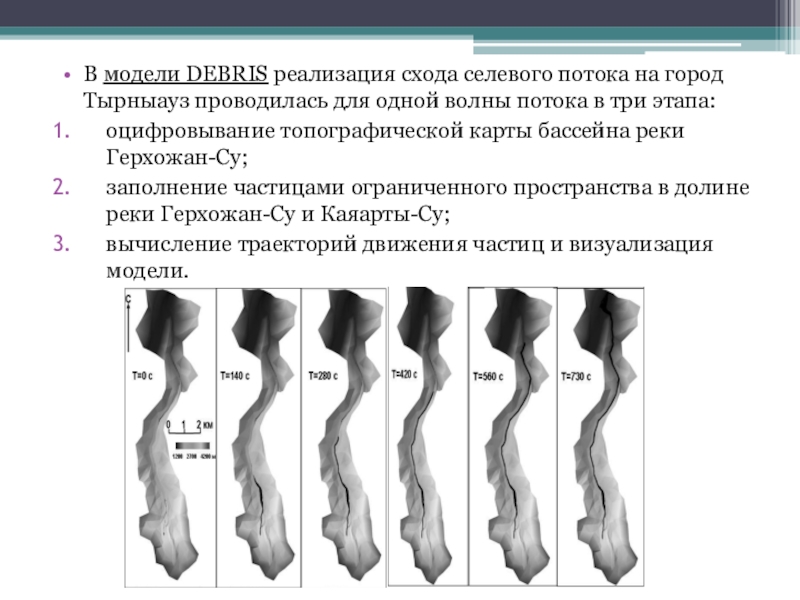
и жидкой фаз потока и длиной фронта. По результатам моделирования строится график.Слайд 11В модели DEBRIS реализация схода селевого потока на город Тырныауз
проводилась для одной волны потока в три этапа:
оцифровывание топографической
карты бассейна реки Герхожан-Су; заполнение частицами ограниченного пространства в долине реки Герхожан-Су и Каяарты-Су;
вычисление траекторий движения частиц и визуализация модели.
Слайд 12Моделирование Уаскаранской ледниковой катастрофы
Исходными данными для моделирования послужила цифровая модель
рельефа бассейна реки Ранраирка. Моделирование схода ледово-каменного потока производилось по
схеме схода оползня, плавно переходящего в поток вещества по мере продвижения вниз по долине. Моделирование в RAMMS хорошо отражает изменение скорости потока и охваченную им площадь на всем протяжении его движения.Слайд 13Заключение
Универсальной математической модели, которая могла бы в точности смоделировать тот
или иной склоновый процесс, на данный момент не существует. В
настоящее время основной целью является как раз создание универсальной трехмерной модели, результаты моделирования в которой будут как можно точнее совпадать с результатами реальных наблюдений.Слайд 14Литература
Божинский А. Н., Назаров А. Н. Динамика двухфазного селевого потока.//Вестник
МГУ. — Сер. 5(Геогр.) — 1999. — № 5. —
С. 15 – 19.Божинский А.Н., Лосев К.С. Основы лавиноведения. Л.: ГИМИЗ, 1987.
Крыленко И.В., Петраков Д.А., Черноморец С.С. Оценка условий формирования селей в бассейне Герхожан-Су и рекомендации по защите города Тырныауза // Устойчивое развитие горныx территорий: проблемы регионального сотрудничества и региональной политики горныx районов: Тез. докл. участников IV междунар. конф. (Владикавказ, 23—26 сентября 2001 г.). — Владикавказ: Ремарко, 2001. — С. 469—471.
Самарский А.А., Михайлов А. П. Математическое моделирование. Идеи. Методы. Примеры. — 2-е изд., испр. — М.: Физматлит, 2001.