Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Молекулярная физика
Содержание
- 1. Молекулярная физика
- 2. Термодинамические потенциалы. Принцип Ле Шателье-Брауна.Третье начало термодинамики (теорема Нернста).
- 3. Термодинамические функции и условия термодинамической устойчивости
- 4. Некоторые формулы математики Пусть имеются три переменные
- 5. Некоторые формулы математикиЭто означает, что независимы лишь
- 6. Слайд 6
- 7. Термин Дифференциал (от лат. differentia — разность, различие) введён
- 8. Слайд 8
- 9. Полный дифференциал, функции f (x, у, z,...)
- 10. Дифференциал (от лат. differentia — разность, различие)
- 11. Рассмотрим гладкую функцию f(x). Проведем касательную к
- 12. Полный дифференциал и его применение
- 13. Полный дифференциал и его применение
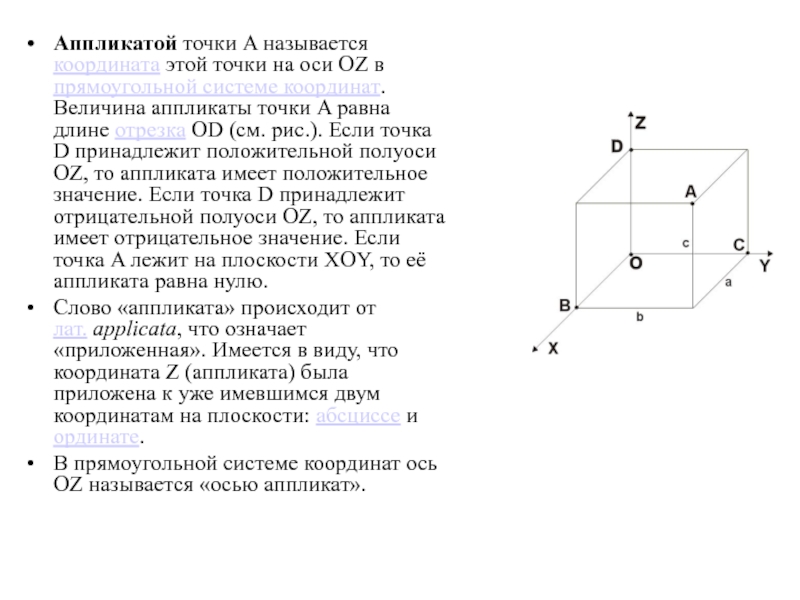
- 14. Аппликатой точки A называется координата этой точки
- 15. Слайд 15
- 16. Некоторые формулы математикиПолные дифференциалы от z, x,
- 17. Некоторые формулы математикиВ термодинамике приходится иметь дело
- 18. Некоторые формулы математикиВ каждой формуле стоит одно
- 19. Некоторые формулы математикиТеперь путаница невозможна и видно,
- 20. Примерz=x2+y3
- 21. Некоторые формулы математикиЕсли известно, что dФ является
- 22. Термодинамические функцииРавновесное состояние ТД системы характеризуется определенным
- 23. Определение термодинамической функцииФункции состояния называются термодинамическими функциями
- 24. Определение термодинамической функцииПусть система, находящаяся в равновесии,
- 25. Определение термодинамической функцииЛогарифмируя Г = Г1Г2 и
- 26. Термодинамическое тождествоВторое начало термодинамики для обратимых процессов
- 27. Свободная энергия или функция ГельмгольцаИз бесчисленного множества
- 28. Свободная энергия или функция ГельмгольцаПри изотермическом процессе
- 29. Свободная энергия или функция ГельмгольцаЯсно, что свободная
- 30. Термодинамическая функция ГиббсаОна определяется равенствомЭта функция называется также термодинамическим потенциалом Гиббса.
- 31. Соотношения МаксвеллаКаждая из термодинамических функций U, H,
- 32. Соотношения МаксвеллаВычислим полные дифференциалы от термодинамических функций.
- 33. Пример1. Внутренняя энергия По первому началу ТД
- 34. Пример 2. Энтальпия H=U+pV
- 35. Пример 3. Свободная энергия (Гельмгольц 1882) δA=pdV=δQ-dU=TdS-dU→
- 36. Пример 4. ТД потенциал Гиббса (свободная энтальпия)
- 37. Соотношения МаксвеллаИз этих выражений на
- 38. Слайд 38
- 39. Зачем это все надо?В ТД был один
- 40. Основной критерий термодинамической устойчивости Состояние равновесия адиабатически
- 41. Критерий термодинамической устойчивостиОбщая теория термодинамической устойчивости была
- 42. Критерий устойчивости для системы с постоянными объемом
- 43. Критерий устойчивости для системы
- 44. Критерий устойчивости для системы с постоянными объемом
- 45. Критерий устойчивости для системы с постоянными температурой
- 46. Принцип Ле Шателье — Брауна Устойчивость состояния
- 47. Правило ЛенцаИндукционный ток в проводнике, в зависимости
- 48. Правило ЛенцаФарадей экспериментально установил, что при изменении
- 49. Рис. иллюстрирует правило Ленца на примере неподвижного проводящего
- 50. Слайд 50
- 51. Правило ЛенцаЕсли металлический проводник передвигается вблизи гальванического
- 52. Рассмотрим некоторые примеры.1. Возьмем соленоид (катушку) C, замкнутый
- 53. Возьмем соленоид C, замкнутый через гальванометр G. Будем удалять
- 54. Индукционный ток всегда имеет такое направление, что
- 55. Слайд 55
- 56. Слайд 56
- 57. Третье начало термодинамикиПервые два начала термодинамики дают
- 58. Третье начало термодинамикиТак как энтропия определяется с
- 59. Слайд 59
- 60. Третье начало термодинамики. Многочисленные опыты показывают, что
- 61. Третье начало термодинамикиЕсли бы можно было охладить
- 62. Третье начало термодинамикиВозникает, однако, вопрос: как бы
- 63. Третье начало термодинамикиНа основании многих опытов, проводившихся
- 64. Третье начало термодинамикиКак мы видели выше, вероятностная
- 65. Третье начало термодинамикиИз третьего начала термодинамики (так
- 66. Слайд 66
- 67. Слайд 67
- 68. Выражение термодинамических функций через статистическую сумму. Если
- 69. Запишем формулу с учетом выражения для S
- 70. Выражения тождественны, если внутренняя энергия определяется выражением
- 71. энтропиявнутренняя энергияэнтальпия
- 72. температура и объемтермодинамическая функция ГиббсаТаким образом, знание статистической суммы позволяет провести полный анализ термодинамического состояния систем.
- 73. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Термодинамические потенциалы.
Принцип Ле Шателье-Брауна.
Третье начало термодинамики (теорема Нернста).
Слайд 4Некоторые формулы математики
Пусть имеются три переменные х, у, z,
связанные между собой формулой
z = z(x, у).Слайд 5Некоторые формулы математики
Это означает, что независимы лишь две из них,
а третья величина является функцией, первых двух. В формуле z=z(x,у)
эта зависимость выражена в такой форме, что независимыми являются величины (х, у), а зависимой величиной — функцией — является z. Однако можно это уравнение решить либо относительно х, либо относительно у и записать Связь между х, у, z в видех = х(у, z); y = y(z, x).
В этом случае в качестве независимых переменных берутся у, z или z, x соответственно. Таким образом, выбор независимых величин может быть произведен по желанию.
Слайд 7Термин Дифференциал (от лат. differentia — разность, различие) введён Лейбницем. Изначально, dx
применялось для обозначения «бесконечно малой» — величины, которая меньше всякой конечной
величины и всё же не равна нулю. Подобный взгляд оказался неудобным в большинстве разделов математики (за исключением нестандартного анализа).Слайд 9Полный дифференциал, функции f (x, у, z,...) нескольких независимых переменных
— выражение , в случае, когда оно отличается от полного приращения Df
= f (x + Dx, y + Dy, z + Dz,…) - f (x, y, z, …) на величину, бесконечно малую по сравнению сСлайд 10Дифференциал (от лат. differentia — разность, различие) в математике, главная
линейная часть приращения функции. Если функция y = f (x)
одного переменного х имеет при х = х0 производную, то приращение Dy = f (x0 + Dx) - f (x0) функции f (x) можно представить в виде Dy = f" (x0) Dx + R, где член R бесконечно мал по сравнению с Dх. Первый член dy = f" (x0) Dх в этом разложении и называется дифференциалом функции f (x) в точке x0. Из этой формулы видно, что дифференциал dy линейно зависит от приращения независимого переменного Dx, а равенство Dy = dy + R показывает, в каком смысле Дифференциал (математич.) dy является главной частью приращения Dy.Слайд 11Рассмотрим гладкую функцию f(x). Проведем касательную к ней в точке
x, и отложим на этой касательной отрезок, такой длины, чтобы
его проекция на ось x была равна Δx. Проекция этого отрезка на ось y называется дифференциалом функции f(x) в точке x от Δx. Таким образом, дифференциал может пониматься как функция двух переменных x и Δx,определяемой соотношением
в частности, разность приращения функции и её дифференциала — бесконечно малая величина:
f(x + Δx) = f(x) + dxf(Δx) + o(Δx).
Слайд 14Аппликатой точки A называется координата этой точки на оси OZ
в прямоугольной системе координат. Величина аппликаты точки A равна длине
отрезка OD (см. рис.). Если точка D принадлежит положительной полуоси OZ, то аппликата имеет положительное значение. Если точка D принадлежит отрицательной полуоси OZ, то аппликата имеет отрицательное значение. Если точка A лежит на плоскости XOY, то её аппликата равна нулю.Слово «аппликата» происходит от лат. applicata, что означает «приложенная». Имеется в виду, что координата Z (аппликата) была приложена к уже имевшимся двум координатам на плоскости: абсциссе и ординате.
В прямоугольной системе координат ось OZ называется «осью аппликат».
Слайд 16Некоторые формулы математики
Полные дифференциалы от z, x, у, определенных последними
формулами, при различных парах величин, взятых в качестве независимых переменных,
имеют такой вид:
х = х(у, z); y = y(z, x); z = z(x, у).
Слайд 17Некоторые формулы математики
В термодинамике приходится иметь дело с полными дифференциалами
различных функций состояния, причем в качестве независимых переменных могут браться
различные пары переменных. Пусть, например, имеется некоторая функция F, которую можно рассматривать как функцию от х, у либо как функцию от х, z. Ee полные дифференциалы в этих случаях имеют такой вид:
Слайд 18Некоторые формулы математики
В каждой формуле стоит одно и то же
выражение
но смысл и значение его совершенно различны: в первом
случае это производная при постоянном значении у, а во втором — при постоянном значении z. Чтобы избежать путаницы, в термодинамике в явном виде обозначается, о каких независимых переменных при вычислении производной идет речь. Например, формулы должны быть записаны следующим образом:
Слайд 19Некоторые формулы математики
Теперь путаница невозможна и видно, что
Если использовать это
условие, то из выражений
получается следующее соотношение между частными производными:
Слайд 21Некоторые формулы математики
Если известно, что dФ является полным дифференциалом и
записывается в виде формулы
где Р и Q - известные функции от х, у, то из определения и свойств полного дифференциала следует, что
(*)
Слайд 22Термодинамические функции
Равновесное состояние ТД системы характеризуется определенным значением U и
S – функций состояния
1) Функции состояния – сколько их?
Уже знаем:
U, S, H, 2) Можно ли найти еще другие? Да, можно.
3)А сколько их надо на практике?
а) Столько, чтобы мы могли полностью описать поведение равновесной ТД системы (Масье 1869)
б) Из моря их надо выбрать те, которые имеют
α) четкий физический смысл
β) через частные производные которых наиболее просто выражаются параметры ТД системы (Гиббс 1873-78)
Оказывается таких всего 4
U, 2. H, 3. F, 4.G – Гиббс – ТД функции или характеристические функции
Все эти функции состояния обладают свойствами ТД функций по Гиббсу только при определенных условиях взаимодействия ТД системы с окружающей средой
Слайд 23Определение термодинамической функции
Функции состояния называются термодинамическими функциями или термодинамическими потенциалами.
Термодинамических функций существует бесчисленное множество, поскольку если известна одна из
них, то какая-либо функция от этой функции также является термодинамической функцией состояния, (мы не останавливаемся на некоторых ограничениях, которые необходимо наложить на выбор функций). Кроме р, V, Т, характеризующих состояние, нам из предшествующего изложения известны функции состояния, называемые внутренней энергией U, энтальпией Н и энтропией S. Внутренняя энергия рассмотрена в первой лекции по ТД , энтальпия определена равенством (H=U+pV), энтропия в общем случае дается формулой Больцмана (S=klnГ). Относительно нее необходимо добавить следующее.Слайд 24Определение термодинамической функции
Пусть система, находящаяся в равновесии, состоит из двух
подсистем. Энтропии системы и подсистем даются формулами
Величины Г, Г1 и
Г2 связаны с вероятностями для системы и подсистем. По формуле умножения вероятностей независимых событий, Г = Г1Г2.
Слайд 25Определение термодинамической функции
Логарифмируя Г = Г1Г2 и учитывая
S=klnГ ,
S1=klnГ1 S2=klnГ2 находим
т. е. энтропия является аддитивной функцией состояния:
энтропия системы равна сумме энтропии составляющих ее частей.Слайд 26Термодинамическое тождество
Второе начало термодинамики для обратимых процессов с учетом равенства
принимает вид
Это равенство является термодинамическим тождеством, поскольку во всех обратимых процессах оно тождественно удовлетворяется.
Слайд 27Свободная энергия или функция Гельмгольца
Из бесчисленного множества других возможных функций
состояния, кроме перечисленных выше, в термодинамике играют важную роль лишь
немногие. Среди них важнейшее значение имеет свободная энергия F; введена в 1882 г. Гельмгольцем.Перепишем ТД тождество в виде
Слайд 28Свободная энергия или функция Гельмгольца
При изотермическом процессе (Т=const) производимая системой
работа может быть представлена в виде
Итак, бесконечно малая работа, совершаемая
системой при изотермическом процессе, является полным дифференциалом и равна взятому с обратным знаком изменению свободной энергии:Слайд 29Свободная энергия или функция Гельмгольца
Ясно, что свободная энергия является функцией
состояния, поскольку она, согласно последней формуле, является функцией от функций
состояния.Следовательно, при изотермических процессах она играет роль потенциальной энергии: ее изменение, взятое с обратным знаком, равно произведенной работе.
Но это справедливо только при изотермическом процессе, при произвольном процессе работа, вообще говоря, не равна изменению свободной энергии.
Слайд 30Термодинамическая функция Гиббса
Она определяется равенством
Эта функция называется также термодинамическим потенциалом
Гиббса.
Слайд 31Соотношения Максвелла
Каждая из термодинамических функций U, H, F, G может
быть представлена как функция любых двух независимых переменных из р,
V, Т, S, причем S в качестве независимой переменной вводится с помощью термодинамического тождества . Иначе говоря, р, V, Т, S связаны двумя соотношениями — уравнением состояния и термодинамическим тождеством, поэтому только две из них могут быть независимыми.Слайд 32Соотношения Максвелла
Вычислим полные дифференциалы от термодинамических функций. Полный дифференциал dU
определяется по формуле
Остальные нетрудно вычислить:
где для dU
использовано выражение dU=TdS-pdV .Слайд 33Пример1. Внутренняя энергия
По первому началу ТД имеем
dU=δQ-pdV=TdS-pdV → U=U(S,V)
Тогда
Отсюда
Следовательно, при выбранных независимых переменных
S и V, температура Т и давление р могут быть наиболее просто выражены через частные производные U. Следовательно, по Гиббсу, U(S,V) - ТД функция при независимых переменных S и VСлайд 34Пример 2. Энтальпия
H=U+pV dH=d(U+pV)=dU+d(pV)=TdS-pdV+pdV+Vdp=
=TdS+Vdp → H=H(S,p)
Тогда
Отсюда
Следовательно, при выбранных независимых переменных S и p,
температура Т и объем V могут быть наиболее просто выражены через частные производные H. Следовательно, по Гиббсу, H(S,p) - ТД функция при независимых переменных S и pСлайд 35Пример 3. Свободная энергия (Гельмгольц 1882)
δA=pdV=δQ-dU=TdS-dU→ (T=const) →d(TS-U)=-d(U-TS)=-dF
Отсюда
видно, что при Т=const F играет роль потенциальной энергии, т.к.
ее убыль равна произведенной работе. ТогдаF=U-TS
dF=dU-d(TS)=δQ-pdV-d(TS)=TdS-pdV-TdS-SdT= -pdV-SdT → →F=F(T,V)
Отсюда
Слайд 36Пример 4. ТД потенциал Гиббса (свободная энтальпия)
G=F+pV=U-TS+pV
dG=d(F+pV)=dF+pdV+Vdp=-SdT-pdV+pdV+Vdp=-SdT+Vdp → →G=G(T,p)
Отсюда
Следовательно, G(T,p) - ТД функция при независимых переменных T и p
Слайд 37Соотношения Максвелла
Из этих выражений на основании (*)
находим:
Четыре равенства между производными являются соотношениями Максвелла.
Слайд 39Зачем это все надо?
В ТД был один метод – метод
ТД циклов, основанный на понятии квазистатического процесса, т.е. все процессы
исследовались с помощью машины Карно.Теперь есть второй метод! С помощью соотношений взаимности Максвелла можно выразить одни макроскопические свойства системы через другие и использовать исследование одних свойств для выявления других, т.е. можно заменить исследование одного процесса исследованием другого более легко реализуемого
Слайд 40Основной критерий термодинамической устойчивости
Состояние равновесия адиабатически изолированной системы достигается
при максимальности энтропии. Это означает, что все бесконечно близкие состояния,
переход в которые мысленно возможен без подвода и отвода теплоты, имеют меньшую энтропию. Второе начало термодинамики запрещает переход в такие состояния.А это означает, что состояние адиабатической изолированной системы устойчиво при максимальной энтропии системы.
Слайд 41Критерий термодинамической устойчивости
Общая теория термодинамической устойчивости была разработана в 1875
— 1878 гг. американским физиком Д. Гиббсом, который сформулировал следующие
необходимые и достаточные условия устойчивости для изолированной системы:1) при всех возможных изменениях состояния системы, не влияющих на ее энергию, вариация энтропии исчезает или отрицательна;
2) при всех возможных изменениях состояния системы, не влияющих на ее энтропию, вариация ее энергии исчезает или положительна.
Исходя из этих общих условий, Гиббс рассмотрел также и частные случаи и развил теорию термодинамического потенциала.
Слайд 42Критерий устойчивости для системы с постоянными объемом и энтропией.
Неравенство
Клаузиуса ( ) с учетом δQ/T=dS
для бесконечно малого необратимого процесса, самопроизвольно происходящего в системе, имеет видПринимая во внимание первое начало термодинамики, можно переписать:
При постоянстве энтропии (dS = 0) и объема (dV= 0) это дает
т. е. в системе могут самопроизвольно происходить лишь процессы с уменьшением внутренней энергии.
Следовательно, устойчивым является состояние при минимуме внутренней энергии
Слайд 43Критерий устойчивости для системы с
постоянными давлением и энтропией
В этом случае условие
( ) имеет видт. е. в системе могут самопроизвольно происходить лишь процессы с уменьшением энтальпии Н = U + pV.
Следовательно, устойчивым является состояние при минимуме энтальпии.
Слайд 44Критерий устойчивости для системы с постоянными объемом и температурой
При
dV=0 и Т=const неравенство
записывается в виде
т. е. в системе
могут самопроизвольно происходить лишь процессы с уменьшением свободной энергии F =U-TS. Следовательно, устойчивым является лишь состояние при минимуме свободной энергии.
Слайд 45Критерий устойчивости для системы с постоянными температурой и давлением
С
помощью выражения (G=F+pV=U-TS+pV) для термодинамического потенциала неравенство
(
) преобразуется к видуПри постоянных температуре и давлении дифференциалы dТ= 0, dp = 0 и выражение сводится к неравенству
т. е. в системе могут самопроизвольно происходить лишь процессы с уменьшением термодинамического потенциала.
Следовательно, устойчивым является состояние при минимуме термодинамического потенциала.
Слайд 46Принцип Ле Шателье — Брауна
Устойчивость состояния обеспечивается тем, что
при выводе системы из состояния равновесия в ней возникают факторы,
стремящиеся вернуть ее в состояние равновесия. Необходимость возникновения таких факторов вытекает из существования устойчивых состояний. В электродинамике формулировка этого положения известна как правило Ленца. В термодинамике она выражается в виде принципа Ле Шателье — Брауна: если на систему, находящуюся в устойчивом термодинамическом равновесии, воздействуют внешние факторы, стремящиеся вывести ее из этого состояния, то в системе возникают процессы, стремящиеся уничтожить изменения, вызываемые внешними воздействиями.Слайд 47Правило Ленца
Индукционный ток в проводнике, в зависимости от условий его
возникновения, имеет разное направление. Вопрос о направлении индукционного тока в
самом общем виде был разрешен Ленцем. Правило Ленца формулируется следующим образом. Индукционный ток, возникающий в замкнутом контуре, всегда имеет такое направление, что созданное им магнитное поле препятствует любым изменениям магнитного потока, вызывающим появление этого тока. Индукционный ток, как и всякий ток, обладает энергией. Следовательно, получая индукционный ток, мы тем самым получаем электрическую энергию; согласно закону сохранения и превращения энергии, последняя может быть получена только за счет эквивалентного количества энергии какого-нибудь другого вида. Когда мы приближаем, например, к катушке магнит , то возникающий в ней индукционный ток своим магнитным полем отталкивает магнит. Двигая магнит, мы преодолеваем эти силы отталкивания, т. е. совершаем работу, в результате чего механическая энергия превращается в энергию индукционного тока. При выдвигании магнита из катушки совершается работа по преодолению силы притяжения катушки и магнита. Механическая энергия здесь также превращается в энергию индукционного тока. Таким образом, правило Ленца находится в полном соответствии с законом сохранения и превращения энергии.Слайд 48Правило Ленца
Фарадей экспериментально установил, что при изменении магнитного потока в
проводящем контуре возникает ЭДС индукции Eинд, равная скорости изменения магнитного
потока через поверхность, ограниченную контуром, взятой со знаком минус:Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение называется правилом Ленца (1833 г.).
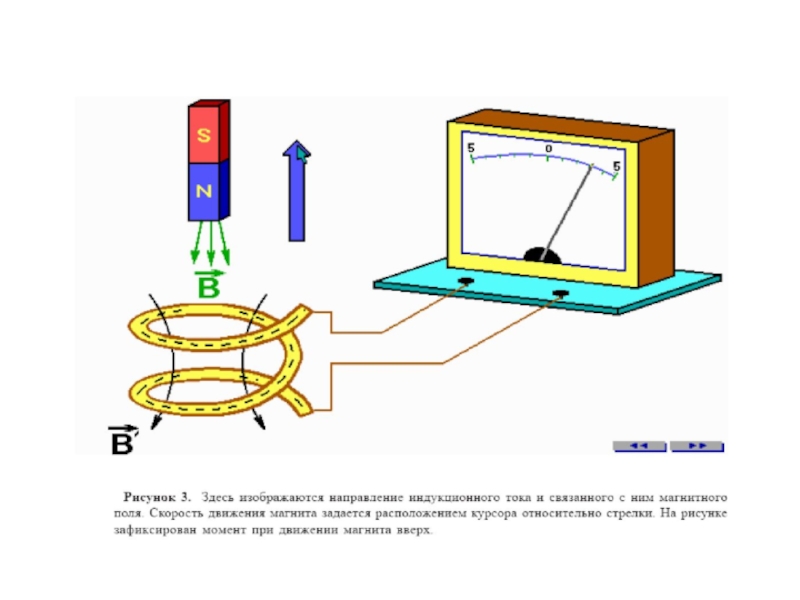
Слайд 49Рис. иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится
в однородном магнитном поле, модуль индукции которого увеличивается во времени.
Иллюстрация
правила Ленца. В этом примере а инд < 0. Индукционный ток Iинд течет навстречу выбранному положительному направлению обхода контура.Слайд 51Правило Ленца
Если металлический проводник передвигается вблизи гальванического тока или вблизи
магнита, то в нем возбуждается гальванический ток такого направления, которое
вызывало бы движение покоящегося провода в направлении, прямо противоположном направлению движения, навязанного здесь проводу извне, в предположении, что находящийся в покое провод может двигаться только в направлении этого последнего движения или прямо противоположном". Профессор петербургского университета Э.Х.Ленц, 1833 год.Правило Ленца основано на обобщении опытов по электромагнитной индукции.
В сжатой форме правило Ленца можно сформулировать так:
возникающий в замкнутом проводнике индукционный ток имеет такое направление, чтобы препятствовать изменению потока магнитной индукции, которое его вызывает.
То есть индукционный ток создает через площадь, ограниченную контуром собственный поток магнитной индукции, компенсирующий изменение потока магнитной индукции, которое его вызывает:
dФ = (В, dS) Ю dФ = B Ч dS Ч cosa,dФ = (В, dS) Ю dФ = B Ч dS Ч cosa,
где a - угол между вектором магнитной индукции внешнего поля и нормалью к плоскости витков соленоида.
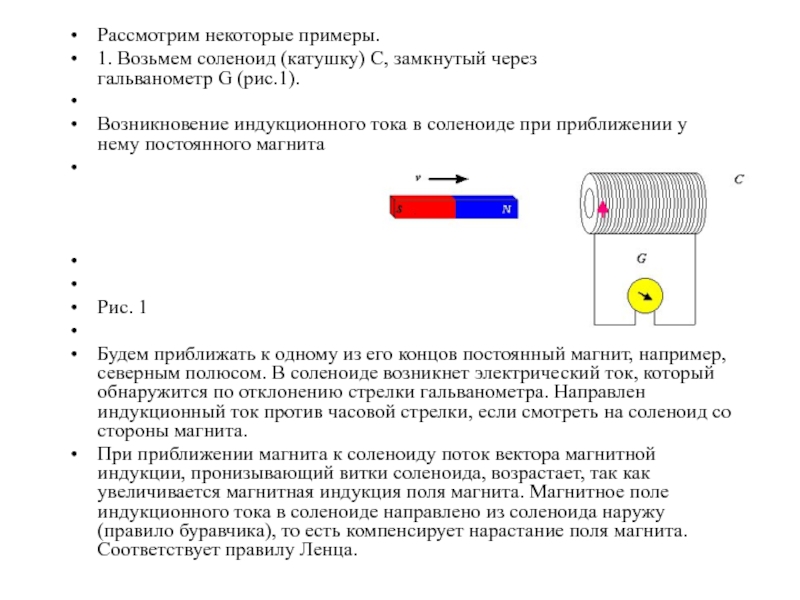
Слайд 52Рассмотрим некоторые примеры.
1. Возьмем соленоид (катушку) C, замкнутый через гальванометр G (рис.1).
Возникновение индукционного
тока в соленоиде при приближении у нему постоянного магнита
Рис.
1Будем приближать к одному из его концов постоянный магнит, например, северным полюсом. В соленоиде возникнет электрический ток, который обнаружится по отклонению стрелки гальванометра. Направлен индукционный ток против часовой стрелки, если смотреть на соленоид со стороны магнита.
При приближении магнита к соленоиду поток вектора магнитной индукции, пронизывающий витки соленоида, возрастает, так как увеличивается магнитная индукция поля магнита. Магнитное поле индукционного тока в соленоиде направлено из соленоида наружу (правило буравчика), то есть компенсирует нарастание поля магнита. Соответствует правилу Ленца.
Слайд 53Возьмем соленоид C, замкнутый через гальванометр G. Будем удалять от одного из
его концов постоянный магнит (рис. 2).
Возникновение индукционного тока в соленоиде
при удалении от него постоянного магнитаРис. 2.
При удалении магнита от соленоида поток вектора магнитной индукции, пронизывающий витки соленоида, убывает, так как уменьшается магнитная индукция поля магнита. Магнитное поле индукционного тока в соленоиде направлено внутрь соленоида (правило буравчика), то есть компенсирует убывание поля магнита. Соответствует правилу Ленца.
Очевидно, что результат опытов не изменится, если магнит будет неподвижен, а соленоид перемещаться.
Анализируя результаты этих двух опытов, можно сделать еще один вывод: при приближении северного полюса магнита к соленоиду индукционный ток создает магнитное поле, индукция которого направлена навстречу индукции магнитного поля магнита, и, следовательно, магнит и соленоид отталкиваются, то есть между ними возникает сила противодействующая движению магнита, которое вызывает возникновение индукционного тока. При удалении магнита магнит и соленоид притягиваются, то есть снова между ними возникает сила противодействующая движению магнита.
Правило Ленца является следствием закона сохранения энергии. Действительно, индукционные токи, как всякие другие электрические токи, совершают некоторую работу. Значит при движении замкнутого проводника (соленоида) в магнитном поле должна быть произведена дополнительная работа внешних сил. Эта и есть та работа, которая возникает за счет сил препятствующих движению магнита.
Изменение потока через витки соленоида C наблюдается и при рассмотрении относительного движения магнита южным полюсом к соленоиду C, замены магнита соленоидом или витком с током, замыкания и размыкания цепи такого соленоида (или витка), а также взаимные повороты соленоида C и элемента, создающего магнитное поле.
Слайд 54Индукционный ток всегда имеет такое направление, что взаимодействие его с
первичным магнитным полем противодействует тому движению, вследствие которого происходит индукция. Это
правило носит название правила Ленца.Правило Ленца стоит в тесной связи с законом сохранения энергии. В самом деле, представим себе, например, что при приближении северного полюса магнита N к соленоиду ток в нем имел бы направление, противоположное тому, какого требует правило Ленца, т. е. что на ближайшем к магниту конце соленоида возникал бы не северный, а южный полюс. В этом случае между соленоидом и магнитом возникли бы не силы отталкивания, а силы притяжения. Магнит продолжал бы самопроизвольно и со все большей скоростью приближаться к соленоиду, создавая в нем все большие индукционные токи и тем самым все более увеличивая силу, притягивающую его к соленоиду. Таким образом, без всякой затраты внешней работы мы получили бы, с одной стороны, непрерывное ускоренное движение магнита к соленоиду, а с другой, все более возрастающий ток в соленоиде, способный производить работу. Ясно, что это невозможно и что индукционный ток не может иметь другого направления, чем то, которое указывается правилом Ленца. В том же можно убедиться, рассматривая и другие случаи индукции.
Рис. Направление индукционного тока, возникающего в контуре: а) при приближении к нему магнита; б) при удалении от него магнита
Слайд 57Третье начало термодинамики
Первые два начала термодинамики дают недостаточно сведений о
поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом
термодинамики, или теоремой Нернста — Планка:энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:
Слайд 58Третье начало термодинамики
Так как энтропия определяется с точностью до аддитивной
постоянной, то эту постоянную удобно взять равной нулю (отметим, однако,
что это произвольное допущение, поскольку энтропия по своей сущности всегда определяется с точностью до аддитивной постоянной). Из теоремы Нернста—Планка следует, что теплоемкости Cp и CV при 0 К равны нулю.Слайд 60Третье начало термодинамики.
Многочисленные опыты показывают, что с понижением температуры
во всякой системе наблюдается тенденция ко все большей степени упорядоченности.
На это указывают исследования строения тел, магнитные их свойства и многие другие данные. Можно полагать, что упорядоченное состояние отвечает меньшей энергии частиц, образующих тело, но что установлению порядка при высоких температурах препятствует тепловое движение.Слайд 61Третье начало термодинамики
Если бы можно было охладить тело до абсолютного
нуля, когда тепловые движения не могут мешать установлению порядка, то
в системе установился бы максимальный мыслимый порядок и этому состоянию соответствовала бы минимальная энтропия.Слайд 62Третье начало термодинамики
Возникает, однако, вопрос: как бы вело себя тело
при абсолютном нуле, если бы над ним совершалась внешняя работа
(например, было бы приложено давление)? Может ли изменяться энтропия тела, находящегося при абсолютном нуле?Слайд 63Третье начало термодинамики
На основании многих опытов, проводившихся при низких температурах,
можно было сделать важный вывод, который формулируется в следующем виде
(Нернст, 1906 г.): при абсолютном нуле температуры любые изменения состояния происходят без изменения энтропии.Это утверждение обычно называют теоремой Нернста. Иногда его возводят в ранг третьего начала термодинамики.
Слайд 64Третье начало термодинамики
Как мы видели выше, вероятностная трактовка понятия энтропии
позволяет сделать вывод о том, что энтропия при абсолютном нуле
температуры равна нулю, что, конечно, не противоречит формулировке Нернста.Из того факта, что при Т=0 и энтропия равна нулю, следует, что абсолютный нуль принципиально недостижим, так как нетрудно показать, что если бы существовало тело с температурой, равной нулю, то можно было бы построить вечный двигатель второго рода, что противоречит второму началу термодинамики. Иногда третье начало термодинамики и формулируют как принцип недостижимости абсолютного нуля.
Слайд 65Третье начало термодинамики
Из третьего начала термодинамики (так будем его называть)
следуют важные выводы о поведении вещества при очень низких температурах.
Так, например, из него вытекает, что с понижением температуры теплоемкость тел должна стремиться к нулю вместе с температурой, а при абсолютном нуле она должна быть равна нулю. Опыт хорошо подтверждает эту тенденцию. Можно показать, что должны стремиться к нулю (а при Т = 0 стать равными нулю) коэффициент теплового расширения тел, коэффициент сжимаемости и т. д. Все это, впрочем, относится к системам, находящимся в равновесном состоянии. У тел, не находящихся в равновесном состоянии, энтропия при абсолютном нуле может и отличаться от нуля.Слайд 68Выражение термодинамических функций через статистическую сумму.
Если в выражение для
средней энергии не входит кинетическая энергия общего упорядоченного поступательного движения
молекул, т. е. если движение центра масс отсутствует, то это выражение можно принять за статистическое определение внутренней энергии. Учитывая, что Z есть функция температуры и объема ипроизводную по в этом выражении следует считать взятой при постоянном объеме:
Слайд 69Запишем формулу с учетом выражения для S в виде
и сравним
ее с дифференциалом от выражения ( -kTlnZ), учитывая, что оно
зависит только от Т и V:Слайд 70Выражения тождественны, если внутренняя энергия определяется выражением , а свободная
энергия выражается в виде
Остальные термодинамические функции выражаются через свободную энергию
формулами:давление