Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Московский государственный университет экономики, статистики и информатики
Содержание
- 1. Московский государственный университет экономики, статистики и информатики
- 2. Реляционная алгебраРеляционная алгебра — это коллекция операций,
- 3. Слайд 3
- 4. Реляционная алгебраОбъединениеВ математике объединение двух множеств представляет
- 5. Примеры отношенийПоставщики S { S#, SNAME,STATUS, CITY
- 6. Объединение отношений Но хотя этот результат
- 7. Объединение отношений Поэтому определение операции реляционного
- 8. Слайд 8
- 9. Объединение отношенийПример. Предположим, что отношения А и
- 10. Пересечение отношений Как и для объединения,
- 11. Пересечение отношенийПример. Снова предположим, что отношения
- 12. Разность отношений Как и для объединения
- 13. Разность отношений Пример. Снова предположим, что
- 14. Произведение отношенийВ математике декартовым произведением (или сокращенно
- 15. Произведение отношений Поэтому реляционной версией декартова
- 16. Произведение отношений Итак, определим (реляционное) декартово
- 17. Слайд 17
- 18. Оператор сокращенияОператор сокращения по сути позволяет получить
- 19. Операция проекции Предположим, что
- 20. Операция проекции
- 21. Операция соединения Предположим, что отношения А
- 22. Операция соединенияТеперь множества { X I, Х
- 23. Слайд 23
- 24. Операция деления Предположим, что отношения А
- 25. Операция деленияДеление представляет собой отношение с заголовком
- 26. Пример деления На рис. приведены
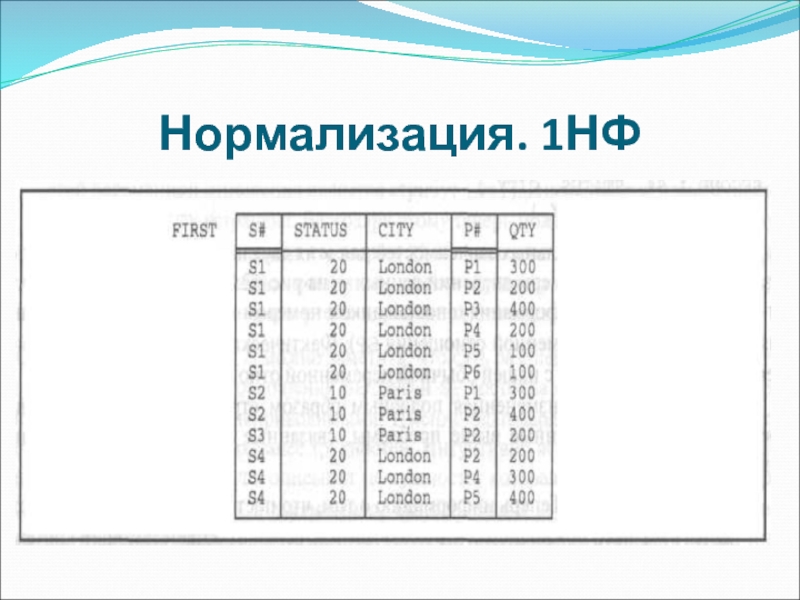
- 27. Нормализация. 1НФ
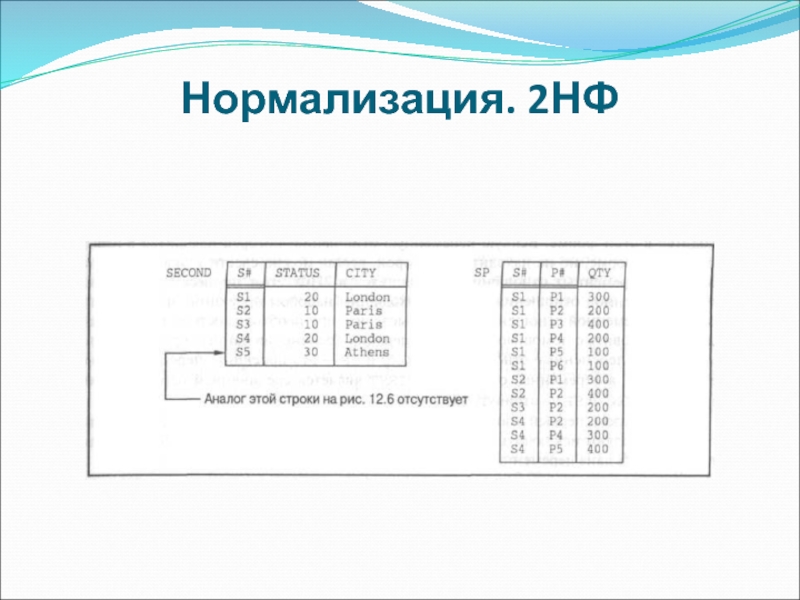
- 28. Нормализация. 2НФ
- 29. Скачать презентанцию
Реляционная алгебраРеляционная алгебра — это коллекция операций, которые принимаютотношения в качестве операндов и возвращают отношение в качестверезультата. Первая версия этой алгебры была определена Коддом. Эта "оригинальная" алгебра включала восемь операций, которые
Слайды и текст этой презентации
Слайд 1Московский государственный университет экономики, статистики и информатики (МЭСИ)
Начальник отдела НИЧ,
к.э.н., доцент Д.Г. Корнеев
Слайд 2Реляционная алгебра
Реляционная алгебра — это коллекция операций, которые принимают
отношения в
качестве операндов и возвращают отношение в качестве
результата.
Первая версия
этой алгебры была определена Коддом.Эта "оригинальная" алгебра включала восемь операций, которые
подразделялись на описанные ниже две группы с четырьмя операциями каждая.
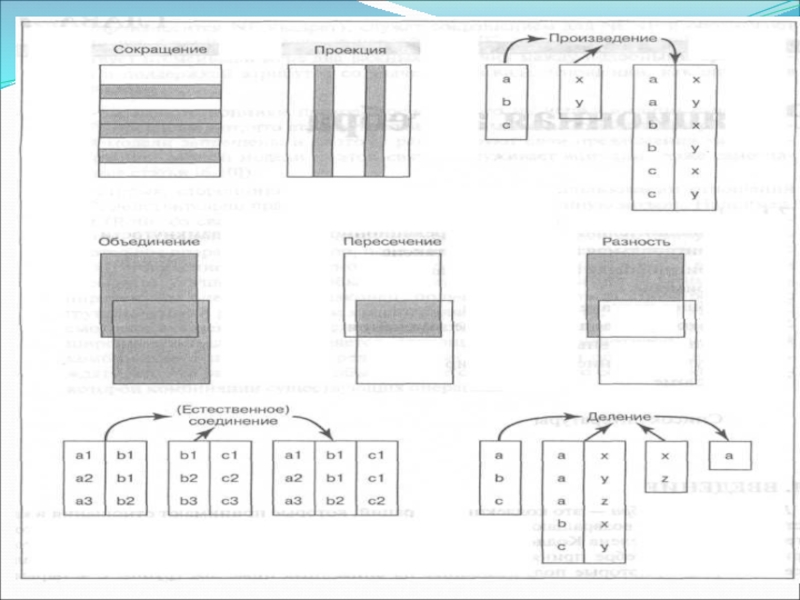
Традиционные операции с множествами — объединение, пересечение, разность и декартово произведение (все они были немного модифицированы с учетом того факта, что их операндами являются именно отношения, а не произвольные множества).
Специальные реляционные операции, такие как сокращение (известное также под названием выборки), проекция, соединение и деление.
Слайд 4Реляционная алгебра
Объединение
В математике объединение двух множеств представляет собой множество всех
элементов, принадлежащих либо к одному из них, либо к обоим
заданным множествам.Поскольку любое отношение представляет собой (или, скорее, содержит) множество (а именно множество кортежей), оно, безусловно, позволяет формировать объединение двух таких множеств; результатом является множество, состоящее из всех кортежей, присутствующих либо в одном, либо в обоих из заданных отношений.
Например, объединение множества кортежей поставщиков, которые в настоящее время присутствуют в S, и множества кортежей деталей, присутствующих в настоящее время в
отношении Р, безусловно, представляет собой множество.
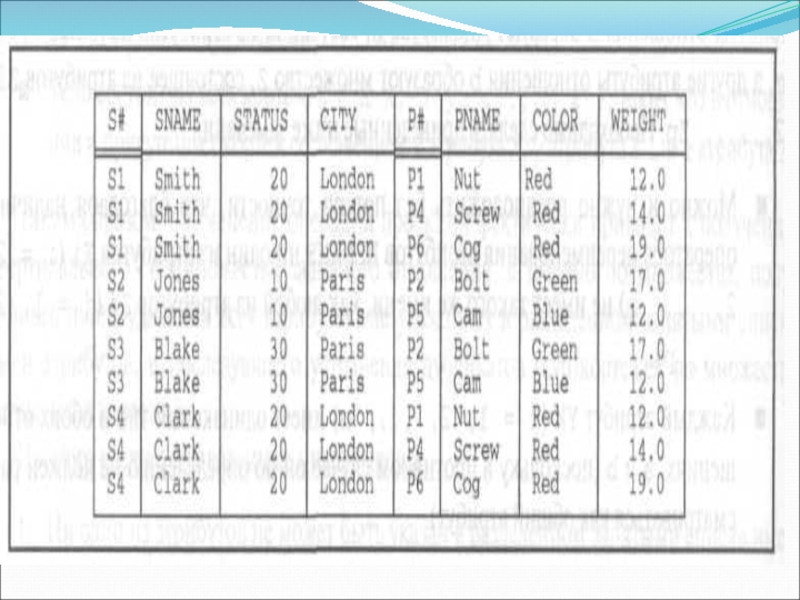
Слайд 5Примеры отношений
Поставщики S { S#, SNAME,
STATUS, CITY }
PRIMARY KEY {
S# }
Поставки P { P#, PNAME, COLOR,
WEIGHT, CITY } PRIMARY
KEY{ P# }
SP { S#, P#, QTY }
PRIMARY KEY { S#, P# }
FOREIGN KEY { S# } REFERENCES S
FOREIGN KEY { P# } REFERENCES P
Слайд 6Объединение отношений
Но хотя этот результат можно назвать множеством,
он не является отношением; отношения не могут содержать смесь кортежей
разных типов, поскольку они должны включать однотипные кортежи.А нам требуется, чтобы результат представлял собой отношение, поскольку необходимо сохранить реляционное свойство замкнутости.
Поэтому объединение в реляционной алгебре не полностью соответствует общему определению
объединения в математике; скорее, оно является объединением особого рода, в котором два входных отношения должны принадлежать к одному типу.
Слайд 7Объединение отношений
Поэтому определение операции реляционного объединения должно быть
таким: если даны отношения А и В одного и того
же типа, то объединение этих отношений А UNION В является отношением того же типа с телом, которое состоит из всех кортежей t, при-сутствующих в А или В или в обоих отношениях.
Слайд 9Объединение отношений
Пример. Предположим, что отношения А и B имеют вид,
показанный на рис. (оба они получены из текущего значения отношения
поставщиков S;В «А» приведены данные о поставщиках из Лондона, а в «В» — данные о поставщиках, которые поставляют деталь Р1). В таком случае в объединение A UNION В (см. рис. а) входят поставщики, которые либо находятся в Лондоне, либо поставляют деталь Р1, либо соответствуют обоим этим условиям.
Обратите внимание на то, что в результате содержатся три кортежа, а не четыре; по определению отношения никогда не содержат дубликаты кортежей (поэтому, неформально выражаясь, из результатов операции объединения "устраняются дубликаты").
Слайд 10Пересечение отношений
Как и для объединения, и фактически по
той же причине, для реляционной операции пересечения требуется, чтобы ее
операнды принадлежали к одному и тому же типу.Если даны отношения А и В одного и того же типа, то пересечением этих отношений А INTERSECT В является отношение того же типа с телом, состоящим из всех кортежей t,
таких, что t присутствует одновременно в А и В.
Слайд 11Пересечение отношений
Пример.
Снова предположим, что отношения А и
В показаны на рис. Тогда пересечение A INTERSECT В (рис.
б) включает всех поставщиков, которые находятся в Лондоне и поставляют деталь Р1.Слайд 12Разность отношений
Как и для объединения и пересечения, для
реляционной операции разности требуется, чтобы ее операнды принадлежали к одному
и тому же типу.Если даны отношения А и В одного и того же типа, то разностью этих отношений А MINUS В (в указанном порядке), является отношение того же типа с телом, состоящим из всех кортежей t, таких, что t присутствует в А, но не в В.
Слайд 13Разность отношений
Пример. Снова предположим, что отношения А и
В показаны на рис.
Тогда результат операции разности A MINUS
В (рис. в) включает поставщиков, которые находятся в Лондоне и не поставляют деталь Р1; Результат операции разности В MINUS A (рис. г) включает поставщиков, которые поставляют деталь Р1 и не находятся в Лондоне.
Обратите внимание на то, что оператор MINUS характеризуется направленностью (некоммутативностью), так же, как вычитание в обычной арифметике (например, "5 - 2" и "2 - 5" не являются одним и тем же).
Слайд 14Произведение отношений
В математике декартовым произведением (или сокращенно произведением) двух множеств
является множество всех таких упорядоченных пар, что в каждой паре
первый элемент берется из первого множества, а второй — из второго множества.Поэтому декартово произведение двух отношений, неформально выражаясь, представляет собой множество упорядоченных пар кортежей. Но мы снова должны сохранить свойство замкнутости;
Иными словами, необходимо, чтобы результат содержал кортежи как таковые, а не упорядоченные пары кортежей.
Слайд 15Произведение отношений
Поэтому реляционной версией декартова произведения
служит
расширенная форма этой операции, в которой каждая упорядоченная пара кортежей
заменяется одним кортежем, являющимся объединением двух рассматриваемых кортежей.Это означает, что если даны следующие кортежи:
{ Al, A2, . . . , Am}
и
{ B1, B2, ..., Bn }
то теоретико-множественное объединение этих двух кортежей представляет собой приведенный ниже единственный кортеж:
{ Al, A2, ..., Am, Bl, B2, ..., Bn}
Слайд 16Произведение отношений
Итак, определим (реляционное) декартово произведение А TIMES
В отношений А и В,
не имеющих общих атрибутов,
как отношение, заголовок которого представляет собой(теоретико-множественное) объединение заголовков отношений А и В, а тело состоит из
всех кортежей t, таких, что t является (теоретико-множественным) объединением кортежа, принадлежащего к отношению А, и кортежа, принадлежащего к отношению В.
Слайд 18Оператор сокращения
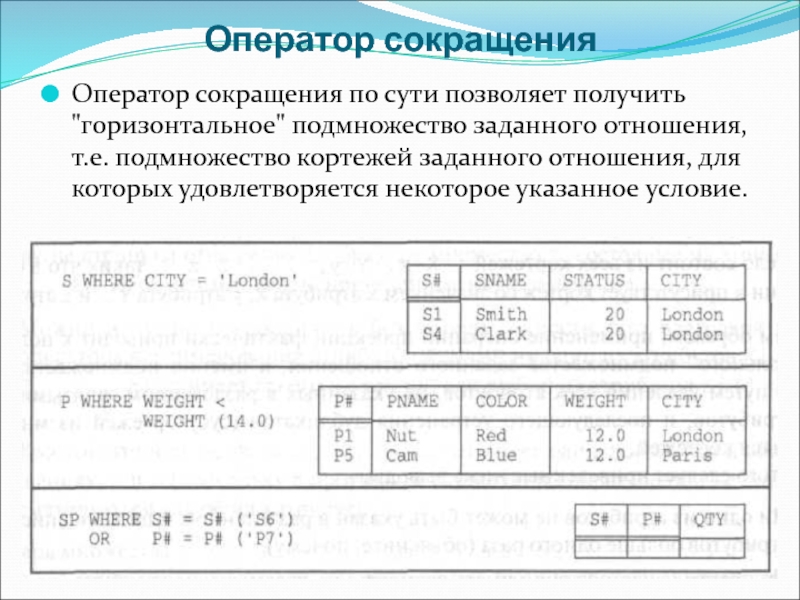
Оператор сокращения по сути позволяет получить "горизонтальное" подмножество заданного
отношения, т.е. подмножество кортежей заданного отношения, для которых удовлетворяется некоторое
указанное условие.Слайд 19Операция проекции
Предположим, что отношение А
имеет атрибуты Х,
Y, . . ., Z (и, возможно, другие атрибуты). В таком случае проекция отношения А по атрибутам X, Y, . . . , Z, которая определяется с помощью следующего выражения:А { X, Y, . . . , Z }
является отношением, соответствующим описанным ниже требованиям:
Его заголовок формируется из заголовка отношения а путем удаления всех атрибутов, не указанных в множестве { X, Y, . . . , Z }.
Тело состоит из всех кортежей { х , у, . . . , z}, таких что в отношении А присутствует кортеж со значением х атрибута X, у атрибута Y... и z атрибута Z.
Слайд 21Операция соединения
Предположим, что отношения А и В, соответствен-но,
имеют следующие атрибуты.
X 1 , Х 2 , . .
. , X m , Y 1 , Y 2 , . . . , Yn (A)Yl , Y2, . . . , Yn, Z l , Z 2 , . . . , Zp (B)
Это означает, что два рассматриваемых отношения имеют общее множество атрибу-
тов Y, состоящее из атрибутов Yl, Y2 , . . . , Yn (и только из этих атрибутов),
Другие атрибуты отношения А образуют множество Х, состоящее из атрибутов X1, Х2, Xm,
Другие атрибуты отношения В образуют множество Z, состоящее из атрибутов Z1, Z2, . . , Zp.
Слайд 22Операция соединения
Теперь множества { X I, Х 2, . .
. , Xm },{ Yl, Y2, . . . ,
Yn } и { Zl, Z2,. . ., Zp } могут рассматриваться, соответствен-но, как три составных атрибута X, Y и Z.В таком случае (естественное) соединение A и B выражается следующим образом.
A JOIN B
Оно представляет собой отношение с заголовком {X, Y, Z} и телом, состоящим из всех таких кортежей {Xх, Yу, Zz}, что любой из этих кортежей присутствует и в отношении A, со значением х атрибута X и значением у атрибута Y, и в отношении B, со значением у атрибута Y и значением z атрибута Z.
Слайд 24Операция деления
Предположим, что отношения А и В, соответственно,
имеют следующие атрибуты:
XI, Х2, . . . ,Хm (А); Yl,
Y2, ..., Yn (В)Здесь ни один из атрибутов Хi (i = 1, 2, . . ., m) не имеет одинакового имени с любым из атрибутов Yj (j = 1, 2, . . ., n).
Пусть отношение С имеет следующие атрибуты:
X I , Х 2 , . . . , Xm, Y l , Y 2 , . . . , Yn (С)
ЭТО означает, что C имеет заголовок, представляющий собой (теоретико-множественное) объединение заголовков А и В. Будем рассматривать множества {XI, Х2, ..., Хm}
{ Yl, Y2, . . ., Yn }, соответственно, как составные атрибуты X и Y. В таком случае операция деления A на B по C (где а — делимое, B — делитель, а C — посредник) может быть
представлена с помощью следующего выражения.
A DIVIDEBY B PER C
Слайд 25Операция деления
Деление представляет собой отношение с заголовком {X} и телом,
состоящим из всех кортежей { X х }, присутствующих в
А, причем таких, что кортеж { Х х, Y у } присутствует в С для всех кортежей { Y у }, присутствующих в В.Иными словами, данный результат состоит из тех значений х, присутствующих в А, для которых соответствующие значения у в С включают все значения у из В.