Мы хорошо знаем, что при решении квадратных уравнений большую роль играет

большую роль играет дискриминант. Но очень часто мы сталкиваемся не

только с задачей о количестве корней, но и с задачей о расположении этих корней на числовой прямой. Например: Сколько корней в зависимости от значений параметра a имеет уравнение 4sin2x-sinx-3=a.
Сделав замену sin x = t, где |t|≤1, мы получаем уравнение
4t2 -t-3-a=0. Таким образом наша задача свелась к определению количества корней квадратного уравнения относительно отрезка [-1;1]. Поэтому рассмотрим более подробно вопрос о нахождении корней квадратного уравнения ax2+bx+c=0 в следующих случаях:
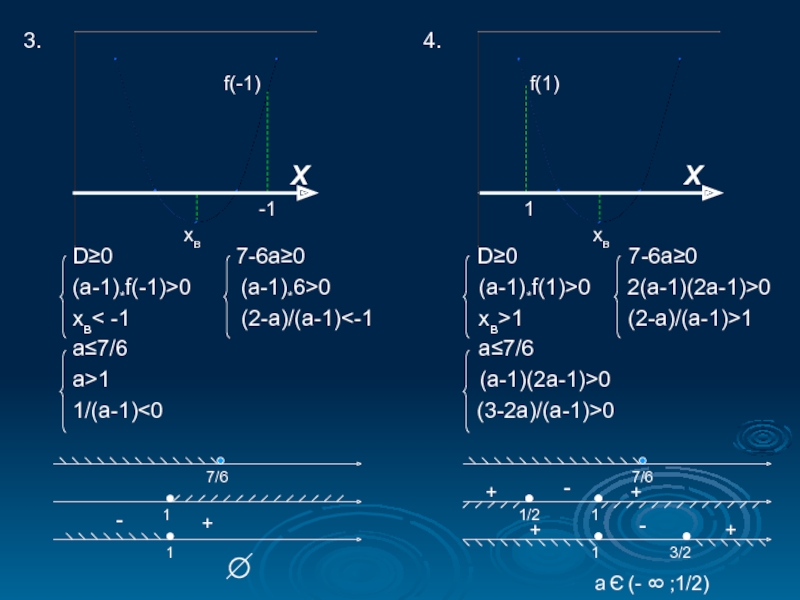
а) оба корня (x1 и x2) меньше заданного числа М.
б) оба корня (x1 и x2) больше заданного числа М.
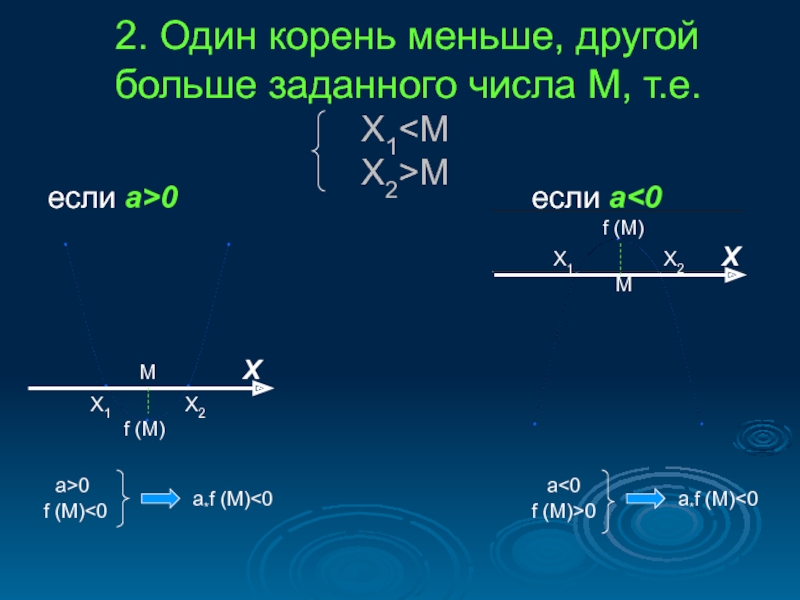
в) x1 x2>M
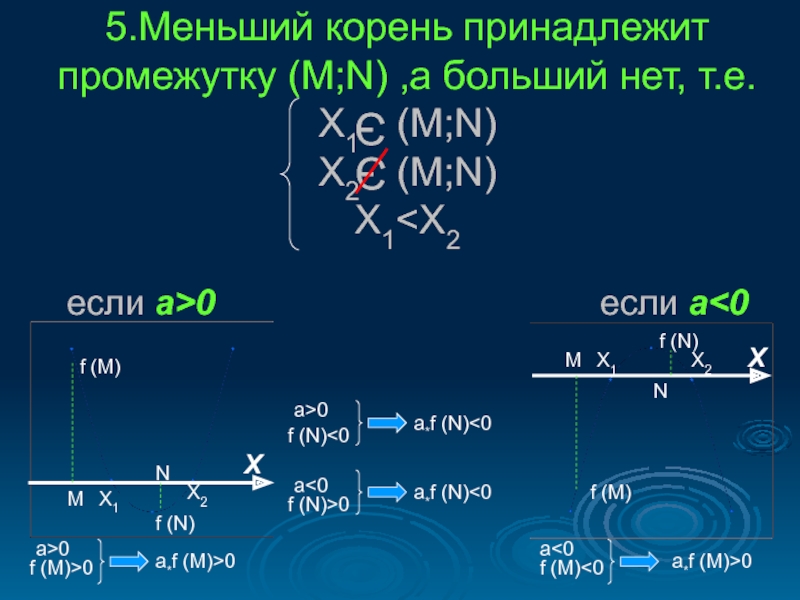
г) один корень принадлежит отрезку (M;N).
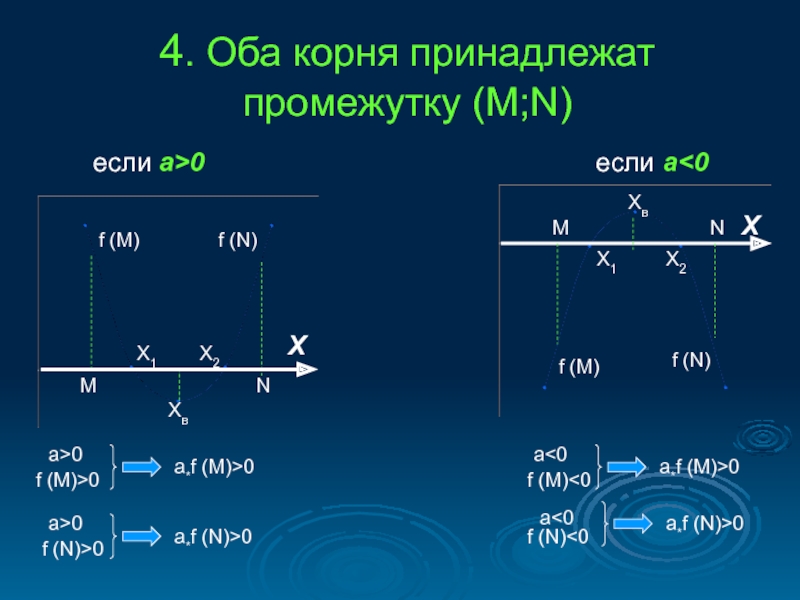
д) оба корня принадлежат отрезку (M;N).
е) и случай, когда ни один из корней не принадлежит отрезку (M;N).
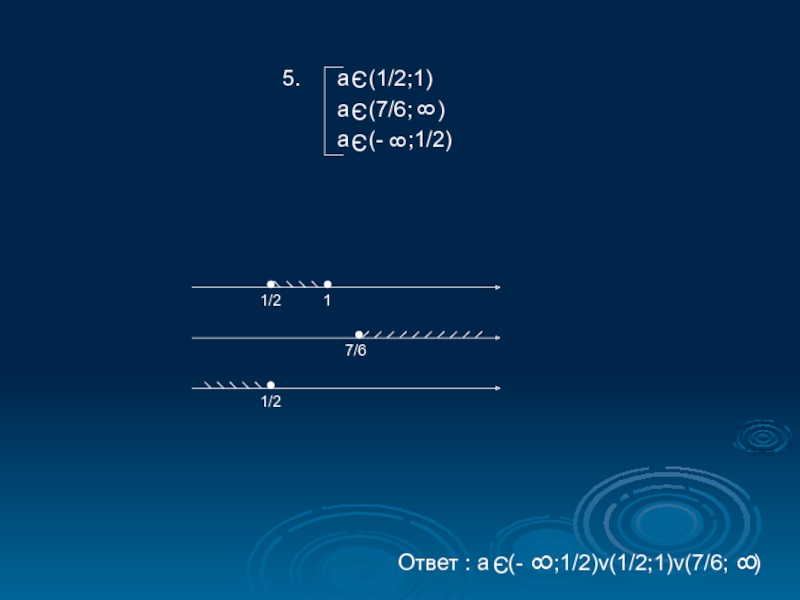
Для удобства рассуждений я рассматривала все эти вопросы при помощи графика квадратного трёхчлена, т.е. параболы y=ax2+bx+c.

относительно точек M и N таких, что
M

трёхчлена.

если a<0

X1

X2

M

f (M)

XВ

X

X1

X2

XВ

X

M

f (M)

a>0

f (M)>0

a*f (M)>0

a<0

f (M)<0

a*f (M)>0

объединяющие

оба графика :
D≥0
xв a*f (M)>0

* a) Уравнение имеет два различных корня, следовательно
D>0
б) Корни уравнения меньше М, следовательно D≥0

уравнения (а-1)x2+(2a-3)x+a-3=0 меньше единицы?
D>0
XВ0
D=(2a-3)2-4(a-1)(a-3)>0

4a-3>0
-(2a-3)/2(a-1)<1 a>3/4 (a-1)(4a-7)>0
(4a-5)/(a-1)>0
(a-1)(4a-7)>0

x1

x2

xв

x

1

f (1)

0,75

1

1,25

1

1,75

Ответ: при a (0,75;1) и (1,75; ).

Э

8

a

a

a

X1M

если a>0 если a<0

X1

X2

X

M

f (M)

X1

X2

M

X

f (M)

a>0

f (M)<0

a*f (M)<0

a<0

f (M)>0

a*f (M)<0

оба графика :
a* f (M)<0

* Т.к. существует точка x=M,
в которой f (M)<0, то парабола
f =ax2+bx+c обязательно будет иметь два различных корня.
Следовательно, требование D>0
НЕОБЯЗАТЕЛЬНО!

(x2;x1) для уравнения (k-1)x2+(k+4)x+k+7=0 ?
a*f (1)

(-10/3;1).

Э

Э

если a>0

если a<0

X1

X2

Xв

f (M)

M

X

Xв

X1

X2

f (M)

X

M

a>0

f (M)>0

a*f (M)>0

a<0

f (M)<0

a*f (M)>0

оба графика :

D≥0
xВ a*f (M)>0

* а) Уравнение имеет два различных корня, следовательно D≥0
б) Корни уравнения больше М, следовательно D>0

больше 0,5?

D>0
XВ>0,5
a*f (0,5)>0
D=(3a)2+8(a+2)a=a(17a+16).
a(17a+16)>0
-3a/2(a+2)>1/2
(a+2)((a+2)/4+3a/2-2a)>0
a(17a+16)>0
(2a+1)/(a+2)<0
(a+2)(2-a)/4>0.

x2

x1

xВ

0,5

f (0,5)

X

a

a

a

-16/17

0

-2

-1/2

-2

2

Ответ: при a (-2;-16/17).

Э

если a<0

X1

X2

Xв

M

N

f (M)

f (N)

X

X1

X2

Xв

X

M

N

f (M)

f (N)

a>0

f (M)>0

a*f (M)>0

a<0

f (M)<0

a*f (M)>0

a>0

a*f (N)>0

a*f (N)>0

f (N)>0

a<0

f (N)<0

D>0 D>0
M a*f (M)>0
a*f (N)>0

Найдём условия,

объединяющие

оба

графика :

где x2 и x1 – корни уравнения (b-2)x2+(b+3)x+b+6=0 ?

D>0
-1 a*f (-1)>0
a*f (-1)>0
D=(b+3)2-4(b-2)(b+6)=-(b-3)(3b+19)>0.
-(b-3)(3b+19)>0
-1<-(b+3)/2(b-2)<1
(-b-3)(3b+19)>0 (b-2)(b-2-b-3+b+6)>0 (-3b -1)/(b-2)>0 (b-2)(b-2+b+3+b+6)>0
(7-b)/2(b-2)<0
(b-2)(3b+7)>0
(b-2)(b+1)>0.

x2

x1

xВ

X

-1

1

f (-1)

f (1)

a

a

a

a

-19/3

3

1/3

2

2

7

-7/3

2

a

-1

2

Ответ:при b (-19/3;-7/3).

Э

(M;N) X2 (M;N) X10

если a<0

Э

Э

X1

X2

M

N

f (M)

f (N)

X

X

X1

X2

M

N

f (M)

f (N)

a>0

f (M)>0

a*f (M)>0

a<0

f (M)<0

a*f (M)>0

a>0

f (N)<0

a*f (N)<0

a<0

f (N)>0

a*f (N)<0

оба графика :

a*f (M)>0
a*f (N)<0

x1>x2 x2 (1;2) x1 (1;2),

(k-2)x2+(k+2)x+k-5=0

a*f (2)<0
a*f (1)>0
(k-2)(k-2+k+2+k-5)>0
(k-2)(4k-8+2k+4+k-5)<0

(k-2)(3k-5)>0
(k-2)(7k-9)<0

где x1 и x2 – корни уравнения

Э

Э

X

x1

x2

1

2

f (1)

f (2)

k

k

5/3

2

2

9/7

Ответ: при k (9/7;5/3).

Э

(M;N) X2 (M;N) X10

если a<0

Э

Э

X1

X2

M

N

f (M)

f (N)

X

X1

X2

M

N

X

f (N)

f (M)

a>0

f (M)<0

a*f (M)<0

a<0

a*f (M)<0

f (M)>0

a>0

f (N)>0

a*f (N)>0

a<0

f (N)<0

a*f (N)>0

оба графика:

f (M)*f (N)<0
a*f (M)<0
a*f (N)>0

x1>x2

x1 (1;2) x2 (1;2), (k+1)x2+(k-4)x+k-7=0

a*f (2)>0
a*f (1)<0
(k+1)((k+1)22+(k-4)2+k-7)>0
(k+1)(k+1+k-4+k-7)<0;

(k+1)(7k-11)>0
(k+1)(3k-10)<0.

где x1 и x2 – корни уравнения

Э

Э

x1

x2

X

1

2

f (1)

f (2)

k

k

-1

11/7

-1

10/3

Ответ: при k (11/7;10/3).

Э

если a<0

X1

X2

f (M)

f (N)

M

N

X

X1

X2

M

N

X

f (M)

f (N)

a>0

f (M)<0

a>0

f (N)<0

a*f (M)<0

a*f (N)<0

a<0

f (M)>0

a<0

f (N)>0

a*f (M)<0

a*f (N)<0

оба графика:

a*f (M)<0
a*f (N)<0

промежуток (-1;2), где x1 и x2 – корни уравнения (k+2)x2+(k-3)x+k-6=0

a*f (-1)<0
a*f (2)<0
(k+2)(k+2-k+3+k-6)<0
(k+2)(4k+8+2k-6+k-6)<0

(k+2)(k-1)<0
(k+2)(7k-4)<0

X

x1

x2

-1

2

f (-1)

f (2)

k

k

-2

-2

4/7

1

Ответ: при k (-2;4/7).

Э

вывод: зная условия расположения корней квадратного уравнения на числовой прямой,

можно с помощью графика всегда составить такие неравенства, которые полностью отразят заданные условия задачи.

Рассмотрим несколько задач, отражающих данную теорию.

больше 1.
1. a+1=0
D≥0

D=9a2-4a*(4+4a)= -16a-7a2 =
xв>1 = -a*(16+7a)
(a+1)*f(1)>0 xв= -b/2a = -(-3a)/2*(a+1) =
=3a/2*(a+1)
f(1)=a+1-3a+4a=2a+1
-a*(16+7a)≥0
3a/2*(a+1)>1
(a+1)(2a+1)>0

a [-16/7;-1)

Э

X

xВ

1

f(1)

- 16 / 7

0

+

+

-

-1

2

-1

-1/2

больше 1, то рассмотрим случай, когда квадратное уравнение будет линейным:

a+1=0
a= -1
(1-1)x2 – 3x*(-1) – 4*(-1)=0
3x-4=0
x=4/3 (4/3>1, следовательно х=4/3 является корнем уравнения)

Ответ: а [-16/7;-1)V{4/3}

Э

меньше 2.
Уравнение не может быть линейным, т.е. 2а-1=0, так как

в условии сказано, что уравнение имеет два корня.
2а-1=0; a=1/2
D>0 D=9-6a+a2 -8a+4=
Xв<2 =a2 -14a+13=(a-1)(a-13)
(2a-1)*f(2)>0 xв= -(3-a)/2*(2a-1)=
= (a-3)/2*(2a-1)
f(2)=(2a-1)*4+(3-a)*2+1=
=6a+3
(a-1)(a-13)>0
(a-3)/2*(2a-1)<2
(2a-1)(6a+3)>0

2

f(2)

xв

X

1

13

1/7

1/2

-1/2

1/2

Ответ:a ( ;-1/2)V(13; )

Э

8

8

-

+

+

+

-

-

-

+

+

+

-

которых уравнение √2(х2 -х-2а2 +2а+2) = х+1;х≥-1 имеет два корня разных

знаков

2(x2 -x-2a2 +2a+2) = x2 +2x+1
2x2 -2x-4a2 +4a+4-x2 -2x-1=0
x2 -4x-4a2 +4a+3=0

f(-1)≥0 f(-1)=1+4-4a2 +4a+3=
f(0)<0 =8-4a2 +4a
f(0)= -4a2 +4a+3

-4(a2 –a-2)≥0
-4a2 +4a+3<0

X

-1

f(-1)

0

-1

2

-1/2

3/2

Ответ: a [-1;-1/2)v(3/2;2]

Э

–(k+1)x+2=0 по абсолютной величине меньше 1.
D=k2 +2k+1-8k=k2 - 6k+1
Xв= -b/2a=(k+1)/(2k)

D>0
f(1)=k-k-1+2=1 xв>-1
f(-1)=k+k+1+2=2k+3 xв<1
k*f(-1)>0
k*f(1)>0
k2 - 6k+1>0 k2 - 6k+1>0
(k+1)/(2k)>-1 (3k+1)/(2k)>0
(k+1)/(2k)<1 (1-k)/(2k)<0
k*(2k+3)>0 k*(2k+3)>0
k>0 k>0

X

1

-1

xв

f(1)

f(-1)

-

-

-

-

-

+

+

+

+

+

+

+

3-2√2

3+2√2

0

0

0

0

-3/2

1

-1/3

Ответ: k (3+2√2; )

Э

+

8

условие -3≤х≤0
1. x2=0; x=0

2. x+1=0; x= -1
2a2 -a-3=0 1=0
a= -1 a=3/2 O
x4-5x2(x+1)=0 x4 –(5x2(x+1))/2=0
x2(x2 -5x-5)=0 x2(x2 -5x/2-5/2)=0
x=0 x=(5+3√5)/2 ( [-3;0]) x=0 2x2 -5x-5=0
x=(5-3√5)/2 x=(5+√65)/4 ( [-3;0])
x=(5-√65)/4

X4 +(3a-2)x2(x+1)+(2a2 –a-3)(x+1)2 =0 (:x2(x+1); x≠0; x≠ -1)
x2/(x+1)+(3a-2)+(2a2-a-3)(x+1)/x2=0
x2/(x+1)=t
t+(2a2 -a-3)/t+3a-2=0; t≠0

Э

Э

x2/(x+1)=3-2a
x2+x(a+1)+(a+1)=0

x2 –x(3-2a)-(3-2a)=0
D=a2+2a+10-4a-4= D=9-12a+4a2+12-8a=
=a2-2a-3=(a+1)(a-3) =4a2-20a+21=4(a-3/2)(a-7/2)
f(-3)=9-3a-3+a+1= f(-3)=9+9-6a-3-2a=
=7-2a =15-8a
f(0)=a+1 f(0)=2a-3 D≥0
xв=-b/2a=-(a+1)/2 xв=-b/2a=(3-2a)/2 f(-3)≥0
f(0)≥0
(a+1)(a-3)≥0 4(a-7/2)(a-3/2)≥0 xв≥-3
7-2a≥0 15-8a≥0 xв≤ 0
a+1≥0 2a-3≥0
-(a+1)/2≥-3 (3-2a)/2≥-3
-(a+1)/2≤0 (3-2a)/2≤0

X

-3

0

f(-3)

f(0)

xв

(a-7/2)(a-3/2)≥0
a≤7/2 a≤15/8
a≥-1 a≥3/2
a≤5 a≤9/2
a≥-1 a≥3/2

-1

-1

-1

7/2

3

5

+

+

-

3/2

3/2

3/2

7/2

15/8

9/2

a [3;7/2]

Э

Ответ:a [3;7/2]v{3/2}

Э

имеет решений.
cosx=t, |t|≤1
2(β2+1) t2+4β2t +1=0

2. f(-1)<0
1.D<0 f(1)<0
D=4β4 -2β2 -2<0 2β2 +2- 4β2 +1<0
β2 =1 β2 = -1/2 2β2 +2 +4β2+1>0
β=±1 (решений нет) 2β2 – 3>0
6β2 + 3<0
(β√2-√3)(β√2+√3)>0
2β2 +1<0 O
β (-1;1) O
3. D=0
2β4 – β2 -1=0
β2=1 β2= -1/2
β=±1
2(1+1)t2 +4t+1=0
(2t+1)2=0; t= -1/2

-1

1

-

+

+

Ответ:β (-1;1)

Э

Э

X

-1

1

f(1)

f(-1)

sinx=t; |t|≤1 2.
(a-1)t2 +2(a -2)t +a+3=0
D/4=a2 -4a+4-(a-1)(a+3)=a2 -4a+
+4 –a2 -2a+3=7-6a
f(1)=a-1+2a-4+a+3=2(2a-1)
f(-1)=a-1-2a+4+a+3=6
D>0 xв=-b/2a=-(a-2)/(a-1)=(2-a)/(a-1) D<0
(a-1)*f(-1)<0 7-6a<0
(a-1)*f(1)<0 a>7/6
7-6a>0
(a-1)*6<0
2(a-1)(2a-1)<0
a<7/6
a<1
(a-1)(2a-1)<0

-1

1

f(-1)

f(1)

1

-1

f(1)

f(-1)

X

X

1

1

7/6

1/2

-

+

+

a (1/2;1)

Э

a (7/6; )

Э

8

4.






D≥0 7-6a≥0 D≥0 7-6a≥0
(a-1)*f(-1)>0 (a-1)*6>0 (a-1)*f(1)>0 2(a-1)(2a-1)>0
xв< -1 (2-a)/(a-1)<-1 xв>1 (2-a)/(a-1)>1
a≤7/6 a≤7/6
a>1 (a-1)(2a-1)>0
1/(a-1)<0 (3-2a)/(a-1)>0

1

-1

f(-1)

f(1)

xв

xв

X

X

7/6

7/6

1

1

1

1

1/2

3/2

-

+

+

+

+

+

-

-

a (- ;1/2)

8

Э

5. a (1/2;1)
a (7/6; )
a (- ;1/2)

Э

Э

Э

8

8

1/2

1/2

1

7/6

Ответ : a (- ;1/2)v(1/2;1)v(7/6; )

Э

8

8

Дорофеев Г.В.
«Алгебраические уравнения и неравенства»
А.И.Азаров, О.М.Гладун, В.С.Федосенко
«Подводные рифы экзаменов»
А.Г.Мерзляк, В.Б.Полонский, М.С.Якир