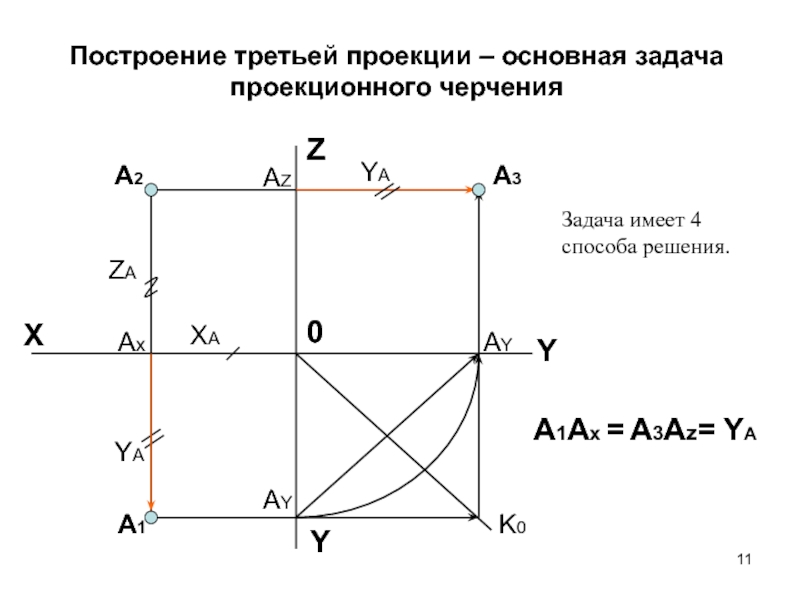
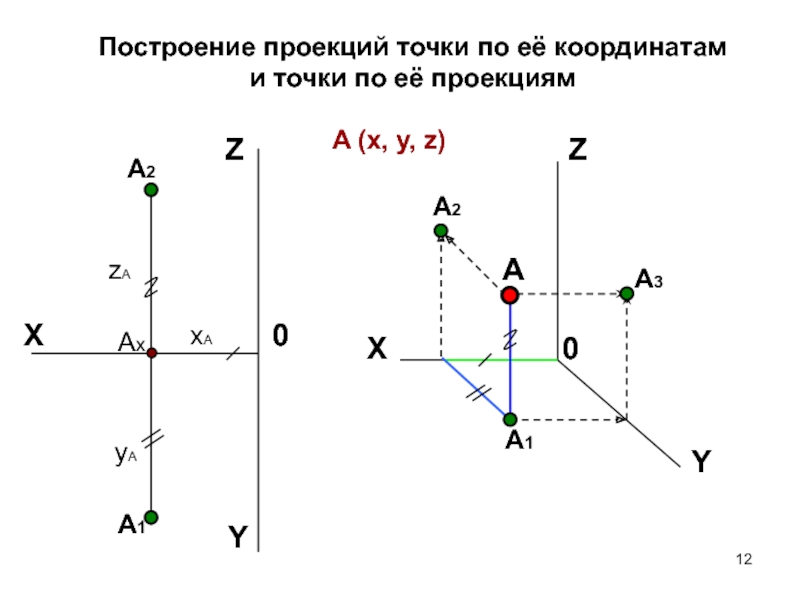
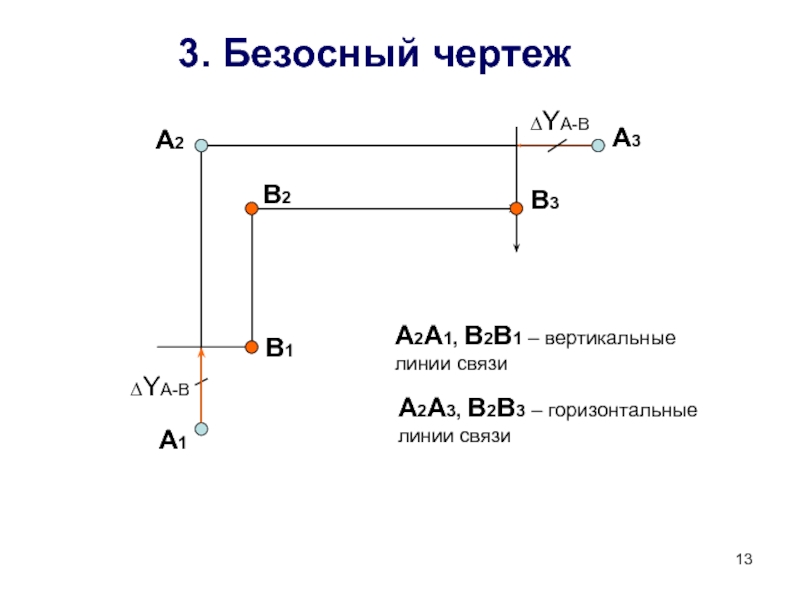
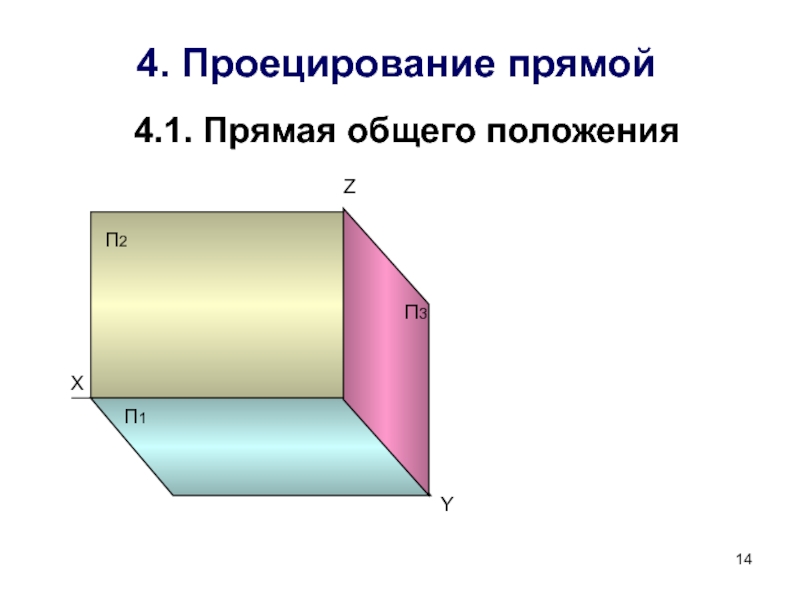
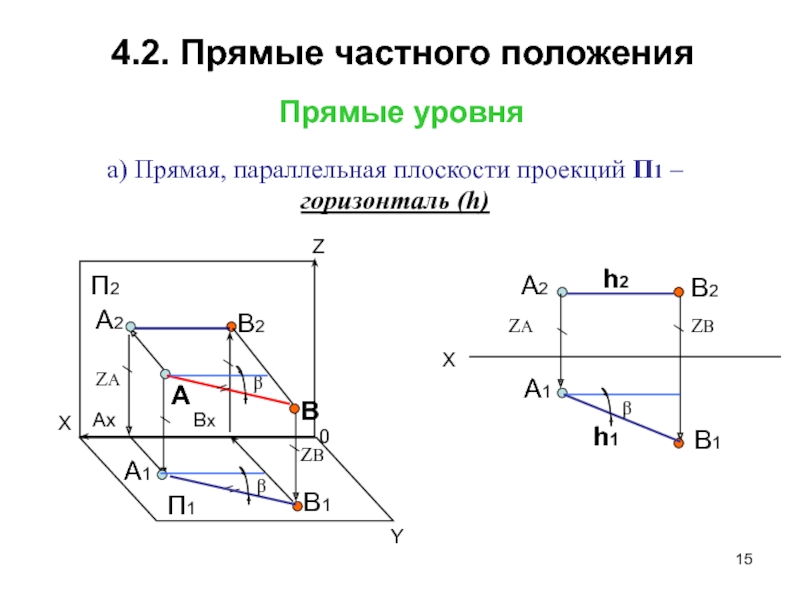
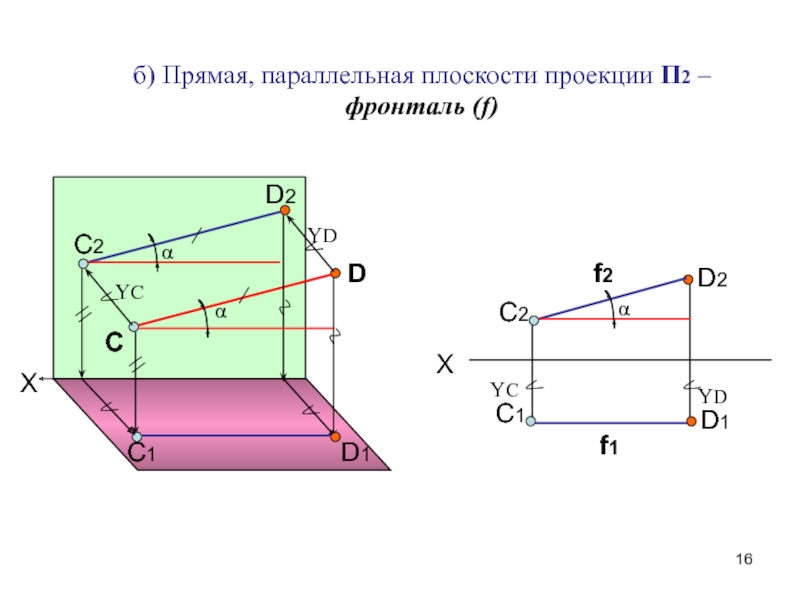
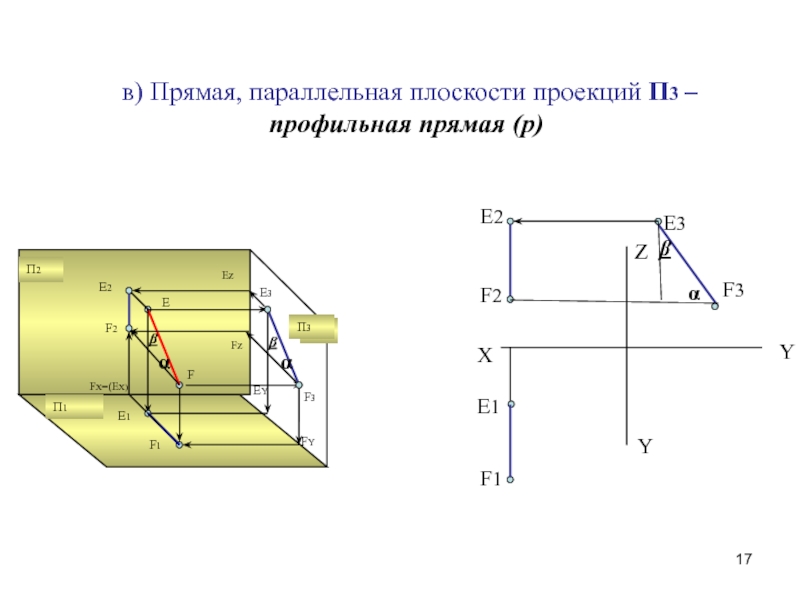
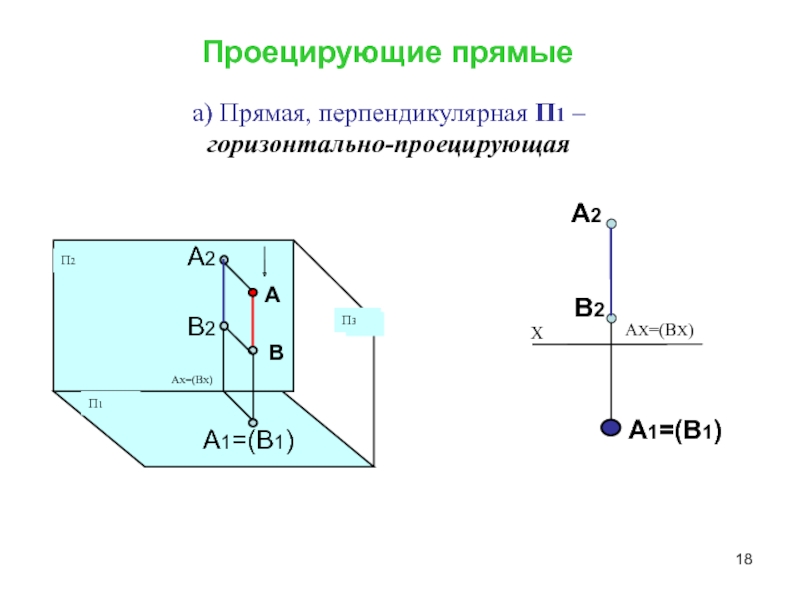
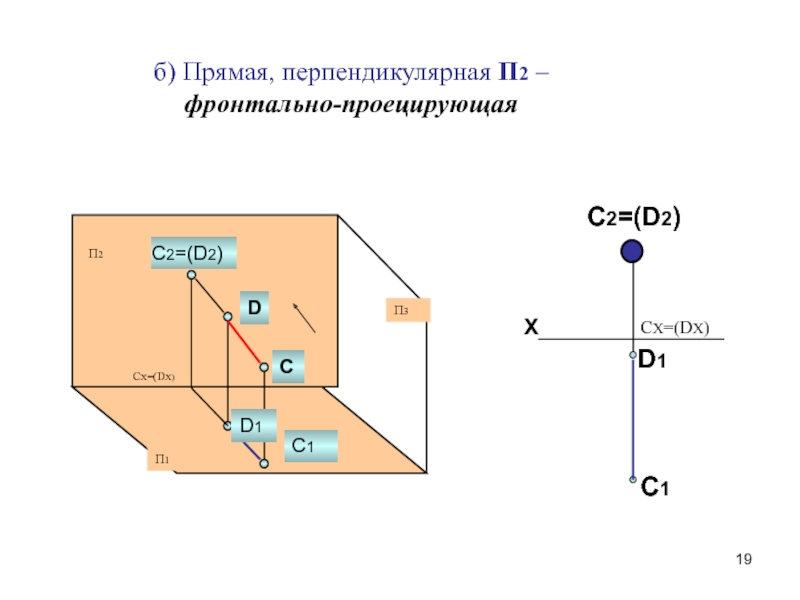
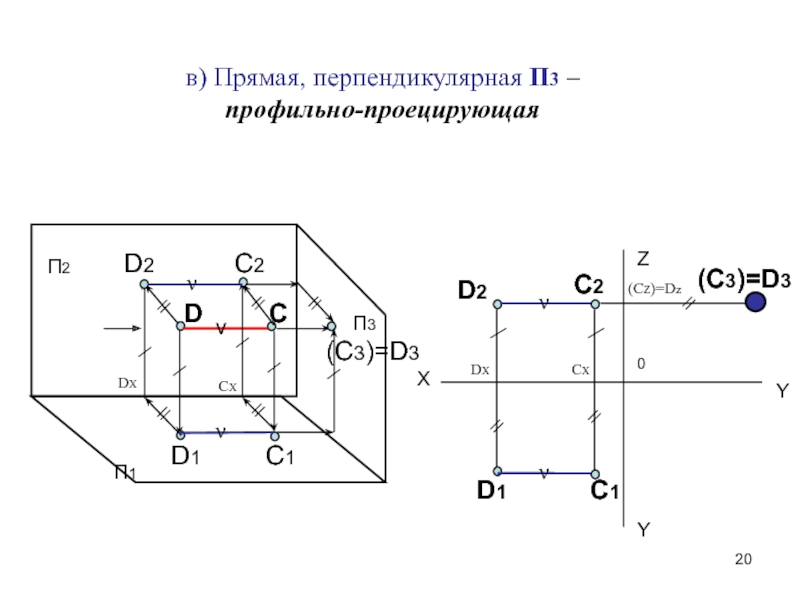
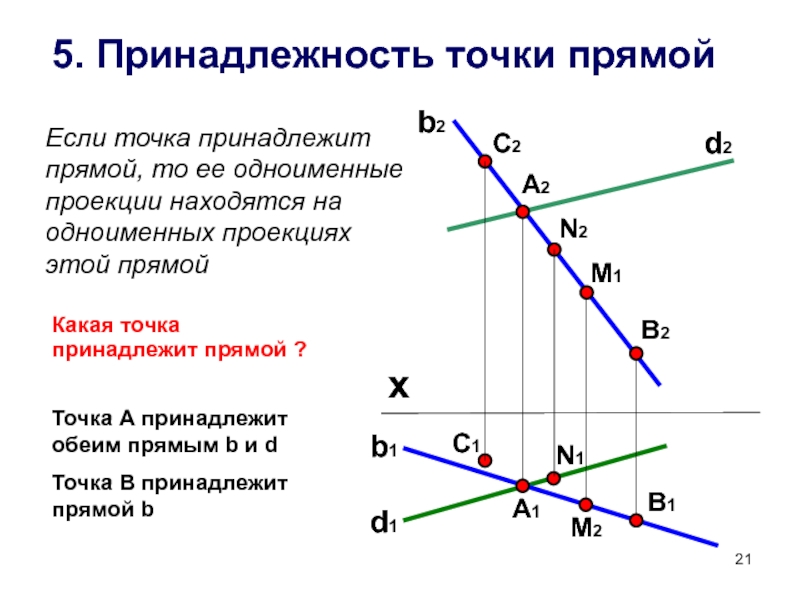
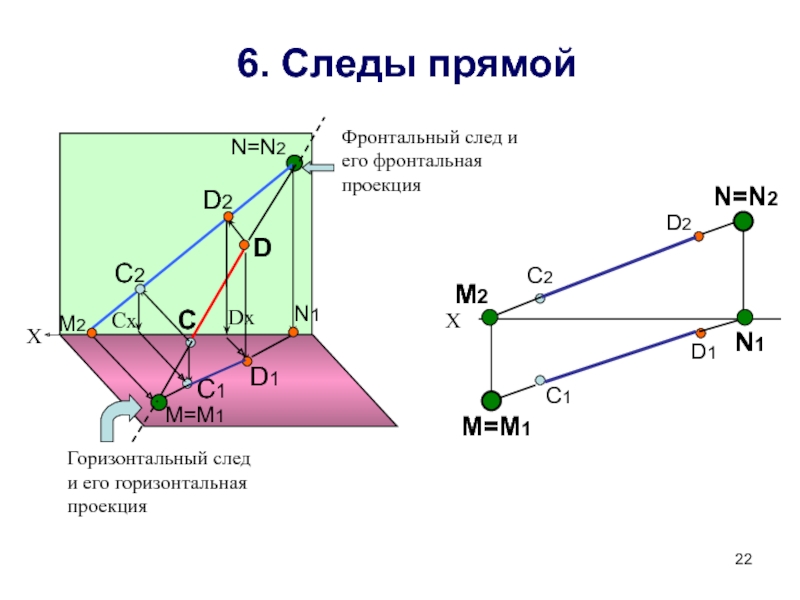
Способы преобразования чертежа.
Лекция 4. Образование поверхностей. Сечение тела плоскостью.
Лекция 5.
Пересечение поверхностей, занимающих частное положение в пространстве.Лекция 6. Пересечение поверхностей общего положения.
Лекция 7. Аксонометрические проекции.
Лекция 8. Некоторые приложения.