Слайд 1Теплотехника
Техническая термодинамика и теплопередача
Овсянников М.К., Орлова Е.Г., Костылев И.И.
ФГБОУ ГУМРФ
Слайд 2ФГБОУ ГУМРФ
Овсянников Михаил Константинович
доктор технических наук, профессор;
Орлова Елена
Геннадьевна
кандидат технических наук, доцент;
Костылев Иван Иванович
доктор технических наук, профессор
кафедры
«Теплотехника, судовые котлы и
вспомогательные установки»
«ГУМРФ имени адмирала С. О. Макарова»
Слайд 3Курс «Техническая термодинамика и теплопередача» предназначен для подготовки инженеров по
специальности 180405 «Эксплуатация судовых энергетических установок»
ФГБОУ ГУМРФ
Основными задачами данного
курса являются:
овладение знаниями об основных законах термодинамики и теплопередачи; характеристиках рабочих сред, теоретических циклах тепловых двигателей и холодильных установок
приобретение навыков выполнения теплотехнических расчётов и моделирования термодинамических процессов.
Слайд 4Оглавление
ВВЕДЕНИЕ
РАЗДЕЛ I. ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
Глава 1. ГАЗ КАК РАБОЧЕЕ ТЕЛО. ОСНОВНЫЕ
ПАРАМЕТРЫ СОСТОЯНИЯ. УРАВНЕНИЕ СОСТОЯНИЯ
Глава 2. ФУНКЦИИ СОСТОЯНИЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
Глава
3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
Глава 4. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Глава 5. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ДВС, ГТУ, КОМПРЕССОРОВ
Глава 6. РЕАЛЬНЫЙ ГАЗ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
Глава 7. ЦИКЛЫ ПАРОТУРБИННЫХ УСТАНОВОК
ФГБОУ ГУМРФ
Слайд 5Оглавление
Глава 8. ТЕЧЕНИЕ УПРУГОЙ СРЕДЫ
Глава 9. ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ХОЛОДИЛЬНЫХ
УСТАНОВОК
Глава 10. ГАЗОВЫЕ СМЕСИ
РАЗДЕЛ II. ТЕПЛОПЕРЕДАЧА
Глава 11.ТЕПЛОПРОВОДНОСТЬ
Глава 12. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН
Глава
13. ТЕПЛОПЕРЕДАЧА
Глава 14. ЛУЧИСТЫЙ ТЕПЛООБМЕН
Глава 15. ОСНОВЫ РАСЧЕТА ТЕПЛООБМЕННЫХ АППАРАТОВ
Приложения
ФГБОУ ГУМРФ
Слайд 6Часть 1
Техническая термодинамика
ФГБОУ ГУМРФ
Слайд 7Первая часть курса «Техническая термодинамика» содержит общие сведения о параметрах,
характеристиках и теплофизических свойствах рабочих сред судовых энергетических установок (в
том числе газовых смесей и двухфазных смесей) и способах их определения; изложение основных законов технической термодинамики; сведения о термодинамических циклах тепловых двигателей и холодильных установок и оценке их эффективности:
ФГБОУ ГУМРФ
Слайд 8Глава 1.
ГАЗ КАК РАБОЧЕЕ ТЕЛО.
ОСНОВНЫЕ ПАРАМЕТРЫ СОСТОЯНИЯ.
УРАВНЕНИЕ СОСТОЯНИЯ
ФГБОУ ГУМРФ
Слайд 91.1. Идеальный газ. Параметры состояния
Идеальным газом принято называть модель газа,
в которой:
а) общий объем предельно упакованных молекул весьма мал по
сравнению с объемом, занимаемым газом;
б) силы взаимного притяжения и отталкивания между молекулами отсутствуют (кроме соударений)
К идеальным газам относятся одно- и двухатомные газы.
ФГБОУ ГУМРФ
Слайд 10Параметры состояния
Состояние любого газа характеризуется тремя основными параметрами:
Удельный объем
υ, м3/кг; υ = V/m,
где m – масса газа,
кг; V – объем, м3.
Величина обратная удельному объему, называется плотностью:
ρ = 1/υ, кг/м3.
2. Давление р, Па = Н/м2 = кг/(м·с2).
3. Температура Т, К; Т = t + 273,15,
где t, 0С – температура по шкале Цельсия.
ФГБОУ ГУМРФ
Слайд 11Давление
1 бар = 105 Па;
1 атм ≈ 101325 Па;
1 МПа
= 106 Па;
1 ат = 1 кгс/см2 ≈ 98067
Па;
750 мм рт. ст. = 105 Па;
10 м вод. ст.≈ 105 Па.
1 атм ≈10 м вод. ст.≈ 105 Па= 1 бар=
=750 мм рт. ст.
ФГБОУ ГУМРФ
Слайд 121.2. Уравнение состояния (Клайперона – Менделеева)
где µ, кг/(кмоль) – молекулярная
масса газа.
Величина R0 = 8314 Дж/(кмоль · К) называется универсальной
газовой постоянной, которая для всех газов одинакова.
ФГБОУ ГУМРФ
Если во всех точках объема параметры занимающего его газа соответственно одинаковы, состояние газа называется равновесным.
Слайд 13Формы записи уравнения состояния
Дж/(кг ·К) - «массовая газовая постоянная»
Или: pυ= RT
Или : pV
= mRT
ФГБОУ ГУМРФ
Слайд 141.3. Термодинамический процесс. Графическое изображение процесса
Непрерывная совокупность изменяющихся состояний рабочего
тела называется термодинамическим процессом.
Если каждое из указанных состояний равновесно, процесс
называется обратимым.
ФГБОУ ГУМРФ
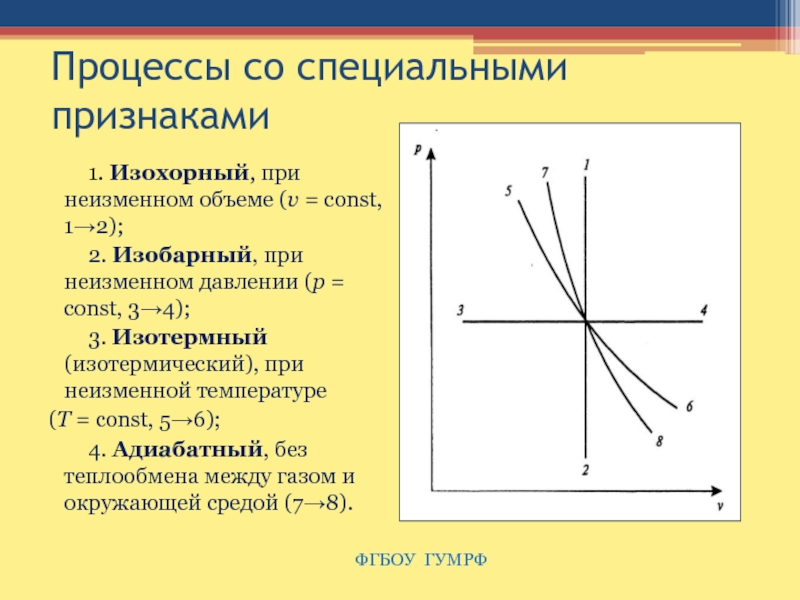
Слайд 15Процессы со специальными признаками
1. Изохорный, при неизменном объеме (υ =
const, 1→2);
2. Изобарный, при неизменном давлении (p = const, 3→4);
3.
Изотермный (изотермический), при неизменной температуре
(T = const, 5→6);
4. Адиабатный, без теплообмена между газом и окружающей средой (7→8).
ФГБОУ ГУМРФ
Слайд 161.4. Теплоемкость
Количество теплоты, необходимое для изменения температуры 1 кг вещества
на 1 К, называется его удельной массовой теплоемкостью
с, Дж/(кг
· К)
Если с=const, то
q = c ∙ ∆T, Дж/кг
Q = c ∙ ∆T∙m, Дж
ФГБОУ ГУМРФ
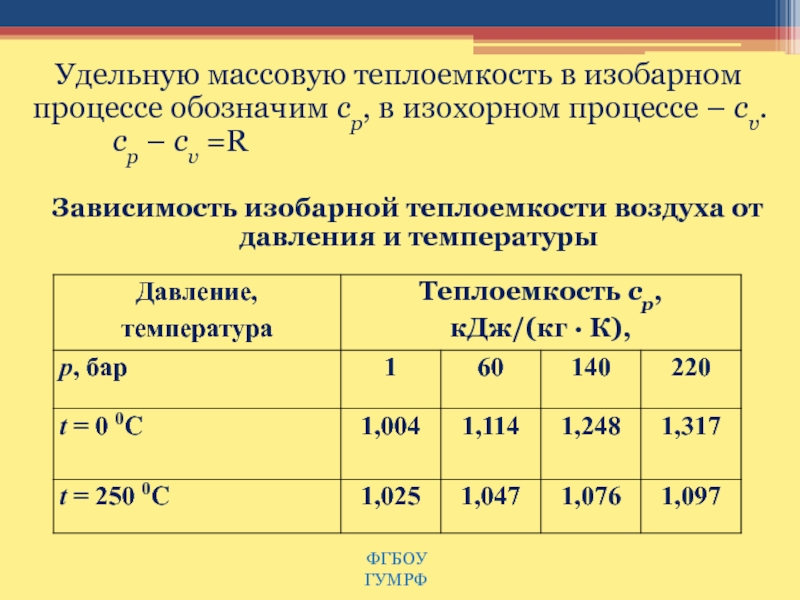
Слайд 17Удельную массовую теплоемкость в изобарном процессе обозначим ср, в изохорном
процессе – сυ. ср – сυ =R
Зависимость изобарной теплоемкости воздуха
от давления и температуры
ФГБОУ ГУМРФ
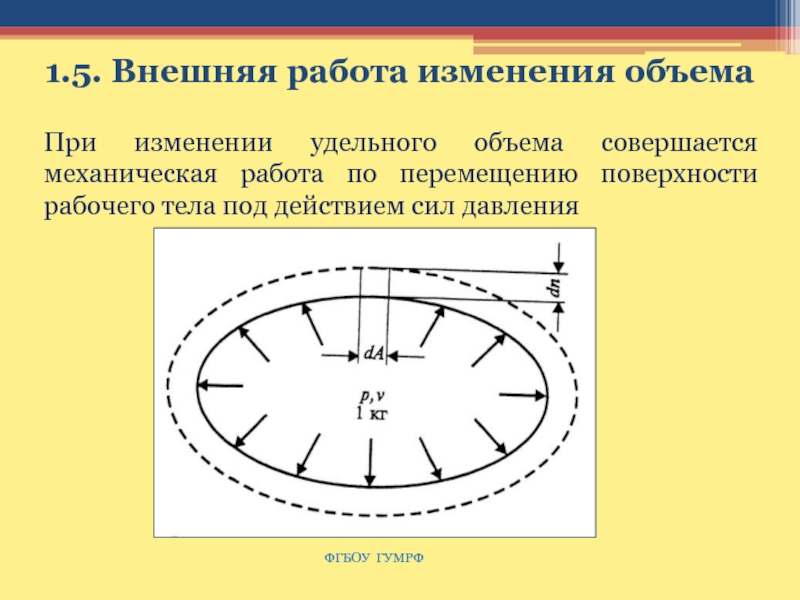
Слайд 181.5. Внешняя работа изменения объема
При изменении удельного объема совершается механическая
работа по перемещению поверхности рабочего тела под действием сил давления
ФГБОУ
ГУМРФ
Слайд 19ФГБОУ ГУМРФ
Удельная работа расширения газа, находящегося под давлением р
при элементарном изменении объема
(dυ = dAdn):
, (Дж/кг)
;
.
Для произвольного количества рабочего тела элементарная работа dL = pdV, (Дж).
Для произвольного процесса, переводящего газ из состояния 1 в состояние 2:
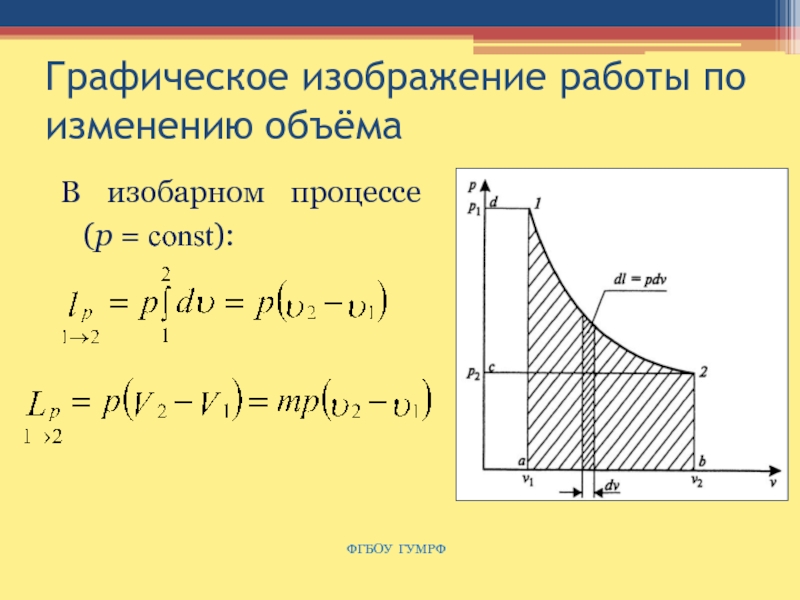
Слайд 20Графическое изображение работы по изменению объёма
В изобарном процессе (р =
const):
ФГБОУ ГУМРФ
Слайд 21Контрольные вопросы и задания к главе 1
Какое состояние называется равновесным
состоянием газа?
Назвать основные термодинамические параметры равновесного состояния газа, их размерности.
Какой
газ называется идеальным газом?
Какая существует связь между абсолютным и манометрическим давлением?
Какие температурные шкалы можно встретить в технической литературе?
Что называется абсолютной температурой?
ФГБОУ ГУМРФ
Слайд 22ФГБОУ ГУМРФ
8. Что называется уравнением состояния газа?
9. Написать уравнение
состояния идеального газа.
10. Какая величина называется удельной массовой газовой постоянной?
11.
Как связаны универсальная и массовая газовые постоянные?
12. Что называется термодинамическим процессом?
13. Назвать характерные термодинамические процессы и их признаки.
14. Что называется теплоемкостью?
15. Назвать размерности теплоемкости газа.
16. Определить различие изобарной и изохорной теплоемкостей.
17. Как определяется работа изменения объема газа?
Слайд 23Глава 2.
ФУНКЦИИ СОСТОЯНИЯ.
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ
2.1. Функции состояния газа
Функция состояния —
это функция, зависящая от нескольких независимых параметров, однозначно определяющих состояние
системы.
ФГБОУ ГУМРФ
Значение функции состояния зависит только от параметров состояния и не зависит от способа перехода системы из одного состояния в другое.
Если дифференциал некоторой термодинамической функции полный, то сама функция является функцией состояния.
Слайд 24Функции состояния
ФГБОУ ГУМРФ
Дифференциал некоторой функции Z =
Z(x,y):
является полным дифференциалом, при условии:
Состояние газа характеризуется тремя параметрами состояния
и тремя функциями состояния:
внутренней энергией (и), энтальпией (i) и энтропией (s).
Слайд 252.1.1. Внутренняя энергия
ФГБОУ ГУМРФ
Под внутренней энергией газа понимается суммарная
энергия движения его частиц.
Она пропорциональна температуре газа Т. Удельная
внутренняя энергия и, Дж/кг (отнесенная к 1 кг массы газа):
и = сυТ , её изменение : dи = сυ dТ , (Дж\кг)
Внутренняя энергия U, Дж (для m кг газа):
U = mсυТ , её изменение : dU = mсυ dТ, (Дж).
Если сυ = соnst, то Δи = сυ ΔТ и ΔU = mсυ ΔТ.
Слайд 262.1.2. Энтальпия
Энтальпией называется полная энергия не перемещающегося газа, которая складывается
из внутренней энергии и энергии упругого сжатого объема (pV) :
I
= U + pV, Дж;
удельной энтальпией называется энтальпия одного килограмма газа i, Дж/кг, i = u + pυ.
Изменение этальпии: di= cpdT
Если сp= const, то
ФГБОУ ГУМРФ
Слайд 272.1.3. Энтропия
Удельной энтропией называется функция состояния s (Дж/(кг·К), для
которой :
.
С учётом 1-го закона термодинамики:
так как и ,
ФГБОУ ГУМРФ
Слайд 28 Энтропия
ФГБОУ ГУМРФ
Величина
является полным дифференциалом функции s, следовательно s
является функцией состояния.
Энтропия произвольной массы газа S = ms, Дж/К.
Энтропию
называют
мерой вероятности состояния термодинамической системы.
Слайд 292.2. Первый закон термодинамики
ФГБОУ ГУМРФ
Первым законом термодинамики называется закон
сохранения энергии применительно к термодинамической системе.
Подведенная к рабочему телу
теплота расходуется на изменение его внутренней энергии и производство внешней работы изменения объема.
Для 1 кг газа : dq = du+ dl = cυdT + pdυ.
Слайд 30 Контрольные вопросы и задания к главе 2
Что называется внутренней энергией
газа, назвать ее размерность.
Что называется энтальпией газа?
Что называется функцией состояния
газа?
Что называется энтропией газа?
Определить физический смысл энтропии как функции состояния.
Сформулировать первый закон термодинамики.
ФГБОУ ГУМРФ
Слайд 31Глава 3. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ
3.1. Политропный процесс
Термодинамический процесс, единственным отличительным признаком
которого является постоянство теплоемкости cn, называется политропным.
Величина cn, называется удельной
теплоемкостью политропного процесса.
ФГБОУ ГУМРФ
Слайд 32Уравнение политропного процесса
- показатель политропного
процесса
ФГБОУ ГУМРФ
Слайд 333.2. Уравнения характерных термодинамических процессов
Изохорный
Изобарный
Изотермический
Адиабатный
(где k – показатель адиабаты)
cn =
cυ; n = ∞; υ = const
cn = cp; n
= 0; p = const
n = 1; pυ = const
pυk = const
ФГБОУ ГУМРФ
Слайд 343.3. Работа изменения объема газа в политропном процессе
ФГБОУ ГУМРФ
Удельная
работа в политропном процессе:
Слайд 353.3. Работа изменения объема газа в политропном процессе
рυ = р1υ1
= р2υ2 = const
В процессе расширения газ производит положительную работу
(l > 0), при сжатии над газом совершается работа (l < 0).
ФГБОУ ГУМРФ
Для изотермического процесса:
Слайд 36Основные зависимости термодинамических процессов
ФГБОУ ГУМРФ
Слайд 37Основные зависимости термодинамических процессов
ФГБОУ ГУМРФ
Слайд 38Контрольные вопросы и задания к главе 3
1. Какой процесс называется
политропным?
2. Напишите уравнения политропного процесса.
3. Что называется показателем политропного процесса?
4.
Как определяется работа изменения объема в политропном процессе?
5. Изобразите все характерные термодинамические процессы в осях p–υ и T–s.
ФГБОУ ГУМРФ
Слайд 39Глава 4.
ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
4.1. Термодинамический цикл. Тепловой двигатель.
Понятие
термодинамического КПД теплового двигателя.
ФГБОУ ГУМРФ
Слайд 40Термодинамический цикл
Непрерывная замкнутая совокупность термодинамических процессов образует термодинамический цикл.
ФГБОУ ГУМРФ
На протяжении цикла
1 кг рабочего тела получает от теплоисточника
теплоту в количестве q1 и отдает теплоприемнику q2 Дж/кг теплоты.
Слайд 41Тепловой двигатель.
Устройство для многократного воспроизводства термодинамического цикла, в котором
подводимая к рабочему телу теплота преобразуется в механическую работу, называется
тепловым двигателем
ФГБОУ ГУМРФ
Слайд 42Понятие термодинамического КПД
Отношение полезной механической работы цикла (l) к
количеству подведенной к рабочему телу теплоты (q1) называется термическим коэффициентом
полезного действия (КПД) цикла теплового двигателя:
ФГБОУ ГУМРФ
Слайд 434.2. Второй закон термодинамики
Формулировки второго закона термодинамики :
природа стремится к
переходу от менее вероятных состояний к более вероятным
Теплота самопроизвольно может
передаваться лишь от тела более нагретого к менее нагретому. Для передачи тепла в противоположном направлении необходимо затратить работу.
ФГБОУ ГУМРФ
Слайд 444.3. Второй закон термодинамики для обратимого термодинамического цикла.
В результате совершения
термодинамического цикла рабочее тело приходит в начальное состояние , и
его энтропия в конце цикла принимает свое первоначальное значение, следовательно:
(4.1)
ФГБОУ ГУМРФ
Этот интеграл называется интегралом Клаузиуса.
Слайд 45ФГБОУ ГУМРФ
Выражение (4.1) называется математической формулировкой второго закона термодинамики.
Для
нулевого результата суммирования выражения (4.1) необходимо иметь как положительные, так
и отрицательные слагаемые.
Другими словами, для совершения полного термодинамического цикла теплового двигателя к рабочему телу нужно не только подводить теплоту от теплоисточника, но с такой же непреложностью и отводить теплоту в теплоприемник.
Слайд 46ФГБОУ ГУМРФ
Следовательно, с учётом выражения для КПД,
можно утверждать,
что термодинамический КПД земного теплового двигателя всегда меньше единицы.
Другими
словами, вечный двигатель второго рода невозможен (q1 ограничено, q2 ≠ 0).
Это положение является следствием второго закона термодинамики.
Слайд 474.4. Второй закон термодинамики для необратимых процессов.
Согласно второму закону термодинамики
природа стремится к переходу от менее вероятных состояний к более
вероятным.
различные формы энергии могут самопроизвольно переходить в теплоту, но невозможны обратные самопроизвольные превращения теплоты в другие виды энергии. Это отражено в другой формулировке второго закона: любой реальный самопроизвольный процесс необратим.
ФГБОУ ГУМРФ
Слайд 48Второй закон термодинамики для необратимых процессов
ФГБОУ ГУМРФ
Для обратимых циклов
интеграл Клаузиса:
Общая математическая формула второго закона термодинамики:
Для обратимого процесса
знак (=), а для необратимого знак (>) т.к. система переходит в более вероятное состояние.
Слайд 49Второй закон термодинамики для необратимых процессов
dS≥ 0
второй закон термодинамики часто
называют законом возрастания энтропии
ФГБОУ ГУМРФ
Слайд 504.5. Цикл Карно
Рассмотрим цикл, состоящий из двух изотерм и двух
адиабат
ФГБОУ ГУМРФ
Термический КПД Цикла Карно:
Теорема Карно:
КПД цикла Карно не
зависит от свойств рабочего тела
Слайд 51Цикл Карно
ФГБОУ ГУМРФ
В любом другом цикле
q1
≤ q1k q2 ≥q2k
Цикл Карно имеет максимальный для данного
диапазона изменения температуры термический КПД.
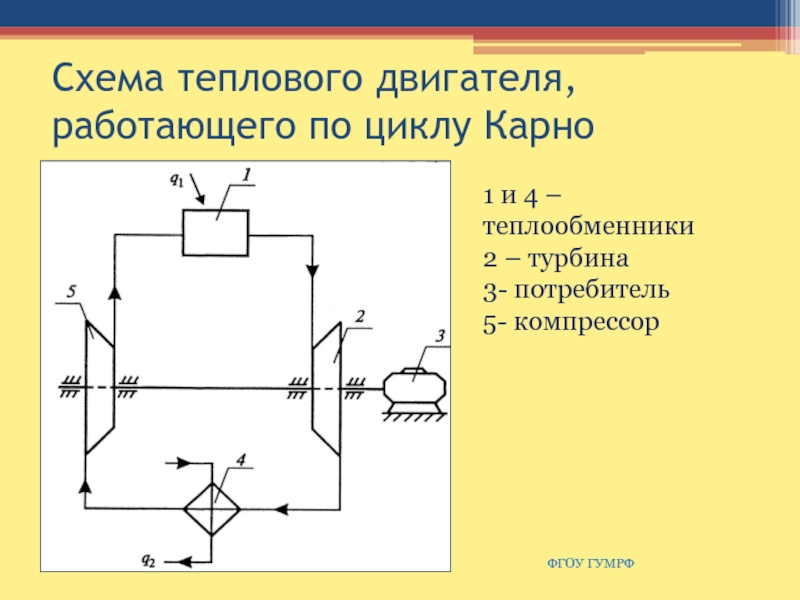
Слайд 52Схема теплового двигателя, работающего по циклу Карно
ФГБОУ ГУМРФ
1 и
4 – теплообменники
2 – турбина
3- потребитель
5- компрессор
ФГОУ ГУМРФ
Слайд 53Контрольные вопросы и задания к главе 4
1. Что называется термодинамическим
циклом?
2. Что называется термодинамическим КПД теоретического цикла теплового двигателя?
3. Сформулировать
второй закон термодинамики.
4. Какой цикл называется обратимым циклом Карно?
5. Определить выражение термического КПД обратимого цикла Карно.
6. От каких параметров зависит величина термического КПД обратимого цикла Карно?
ФГБОУ ГУМРФ
Слайд 54Контрольные вопросы и задания к главе 4
7. Почему обратимый цикл
Карно считается образцовым?
8. Сформулировать теорему Карно.
9. Что называется интегралом Клаузиуса?
10.
Определить различие в интегралах Клаузиуса для обратимого и необратимого термодинамических циклов (равенство и неравенство Клаузиуса).
11. Определить сущность второго закона термодинамики для необратимых процессов (закон возрастания энтропии).
ФГБОУ ГУМРФ
Слайд 55Глава 5.
ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ДВС, ГТУ, КОМПРЕССОРОВ
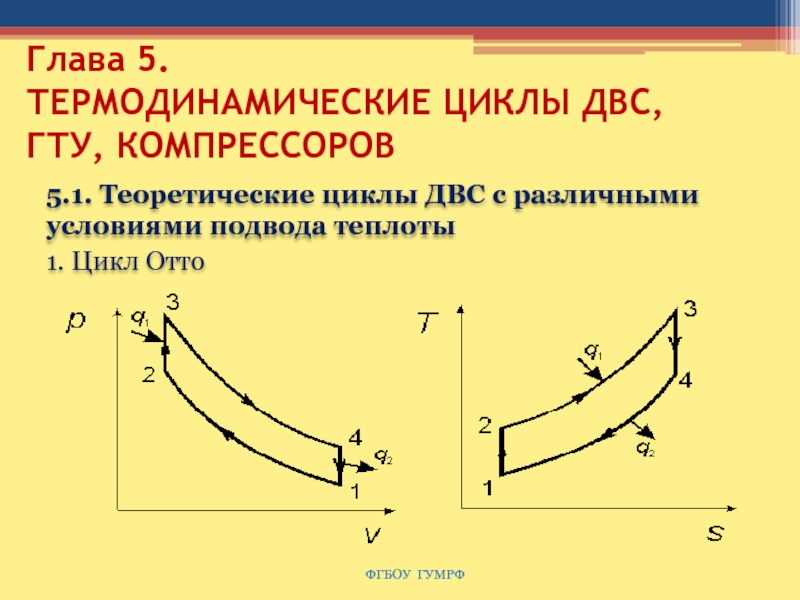
5.1. Теоретические циклы ДВС с
различными условиями подвода теплоты
1. Цикл Отто
ФГБОУ ГУМРФ
Слайд 56Теоретические циклы ДВС с различными условиями подвода теплоты
2. Цикл Дизеля
ФГБОУ
ГУМРФ
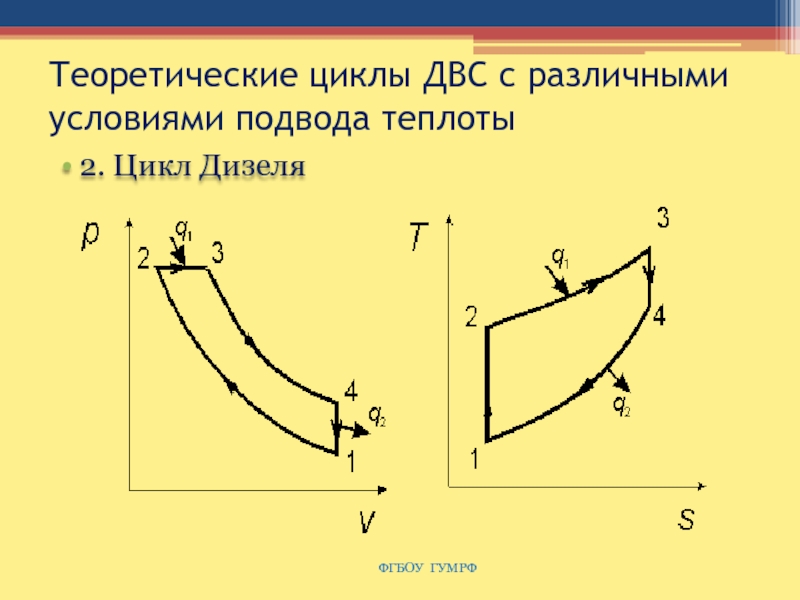
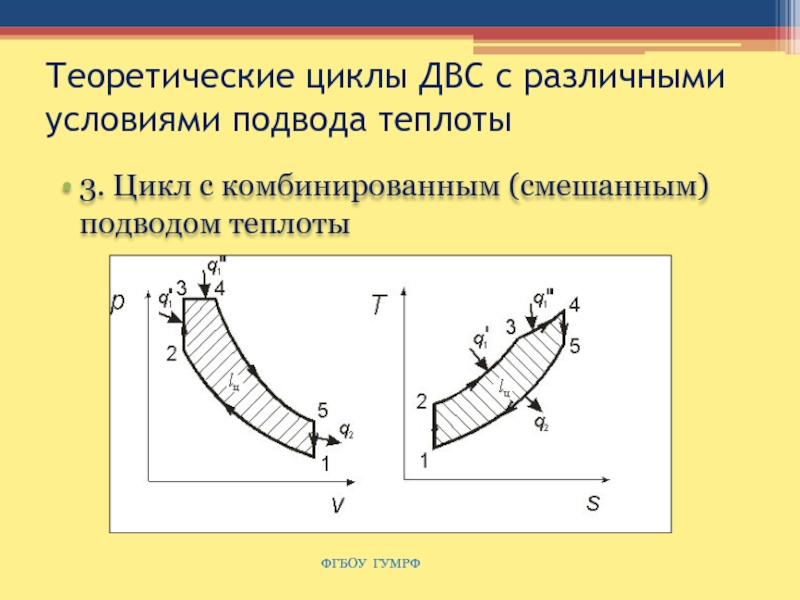
Слайд 57Теоретические циклы ДВС с различными условиями подвода теплоты
3. Цикл с
комбинированным (смешанным) подводом теплоты
ФГБОУ ГУМРФ
Слайд 58Характеристики циклов
степень сжатия
степень повышения давления
степень предварительного расширения
термический
КПД цикла
ФГБОУ ГУМРФ
Слайд 59Термический КПД циклов ДВС
Общая формула
в цикле Дизеля, λ = 1
в цикле Отто, ρ = 1
ФГБОУ ГУМРФ
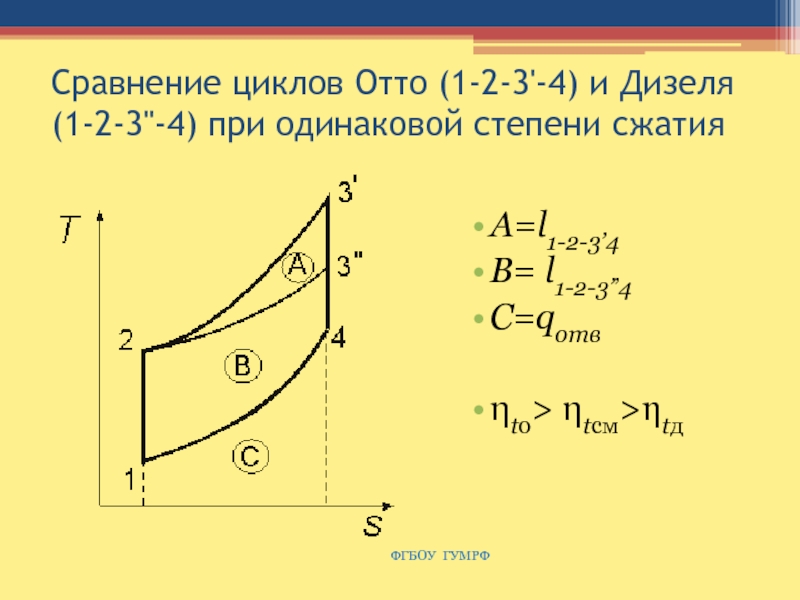
Слайд 60Сравнение циклов Отто (1-2-3'-4) и Дизеля (1-2-3''-4) при одинаковой степени
сжатия
А=l1-2-3’4
B= l1-2-3”4
C=qотв
ηtо> ηtсм>ηtд
ФГБОУ ГУМРФ
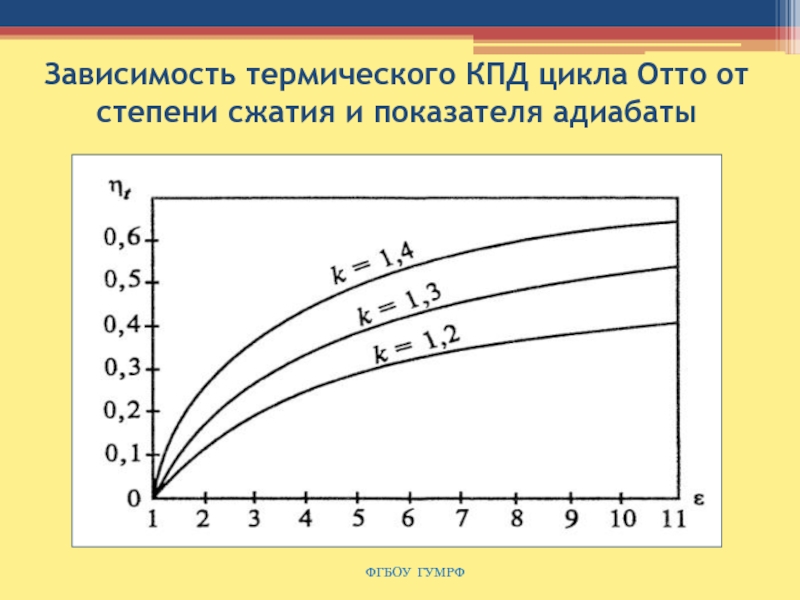
Слайд 61Зависимость термического КПД цикла Отто от степени сжатия и показателя
адиабаты
ФГБОУ ГУМРФ
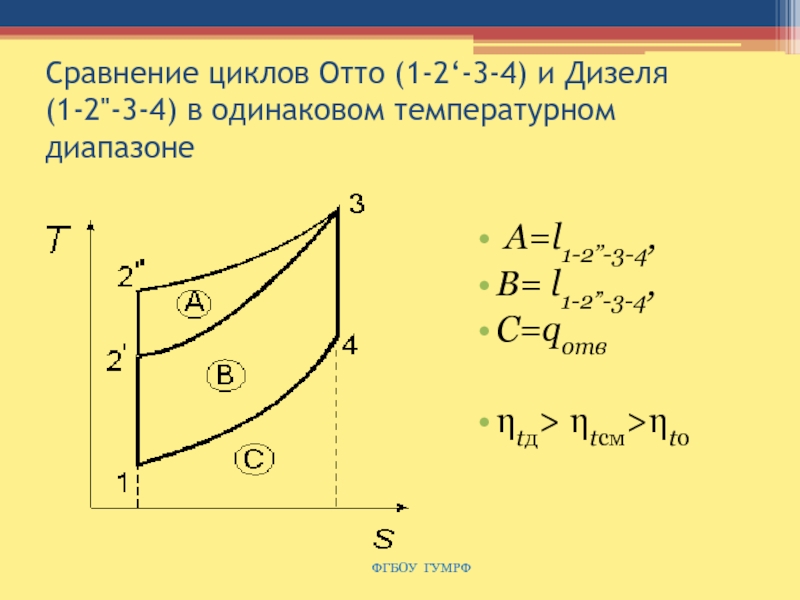
Слайд 62Сравнение циклов Отто (1-2‘-3-4) и Дизеля (1-2''-3-4) в одинаковом температурном
диапазоне
А=l1-2”-3-4,
B= l1-2”-3-4,
C=qотв
ηtд> ηtсм>ηtо
ФГБОУ ГУМРФ
Слайд 635.2. Коэффициенты полезного действия теплового двигателя
Относительный внутренний КПД теплового двигателя:
η0i = l i’/li
где li ‘, li – работа идеального
и реального циклов теплового двигателя соответственно
Индикаторный КПД
ФГБОУ ГУМРФ
где Pi – индикаторная (внутренняя) мощность теплового двигателя, кВт; Вч – часовой расход топлива, кг/ч;
– низшая рабочая теплотворная способность топлива, кДж/кг;
gi – удельный индикаторный расход топлива, кг/(кВт · ч ).
Слайд 64Коэффициенты полезного действия теплового двигателя
механический КПД
эффективный КПД
где ge= Вч/Ре –
удельный эффективный расход топлива, кг/(кВт · ч)
ФГБОУ ГУМРФ
где lе
– работа цикла на валу, двигателя, Дж/(кг · цикл);
Ре – эффективная мощность на валу теплового двигателя, кВт;
Pi–индикаторная мощность теплового двигателя, кВт.
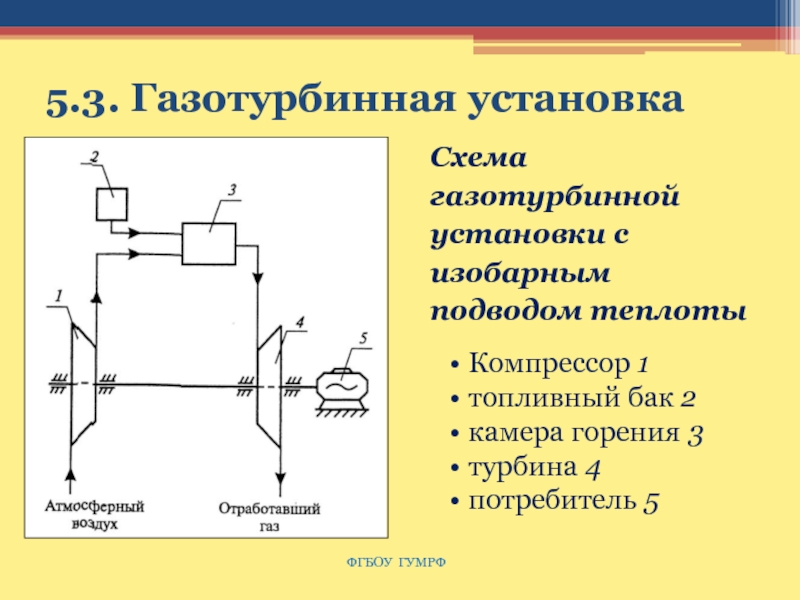
Слайд 655.3. Газотурбинная установка
Схема газотурбинной установки с изобарным подводом теплоты
Компрессор 1
топливный
бак 2
камера горения 3
турбина 4
потребитель 5
ФГБОУ ГУМРФ
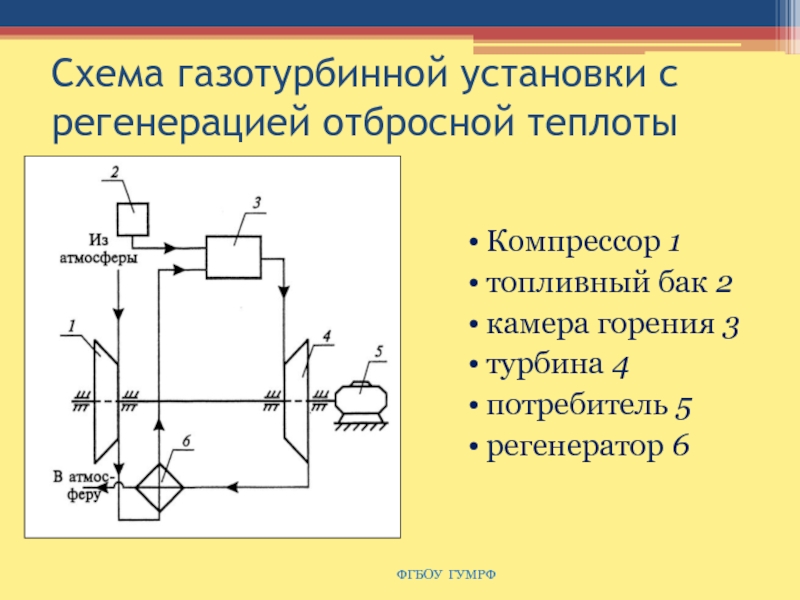
Слайд 67Схема газотурбинной установки с регенерацией отбросной теплоты
Компрессор 1
топливный бак 2
камера
горения 3
турбина 4
потребитель 5
регенератор 6
ФГБОУ ГУМРФ
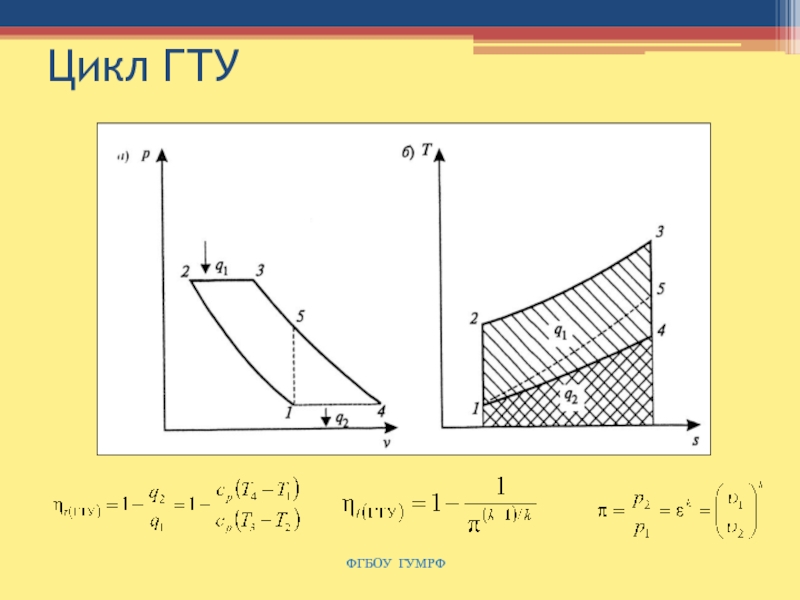
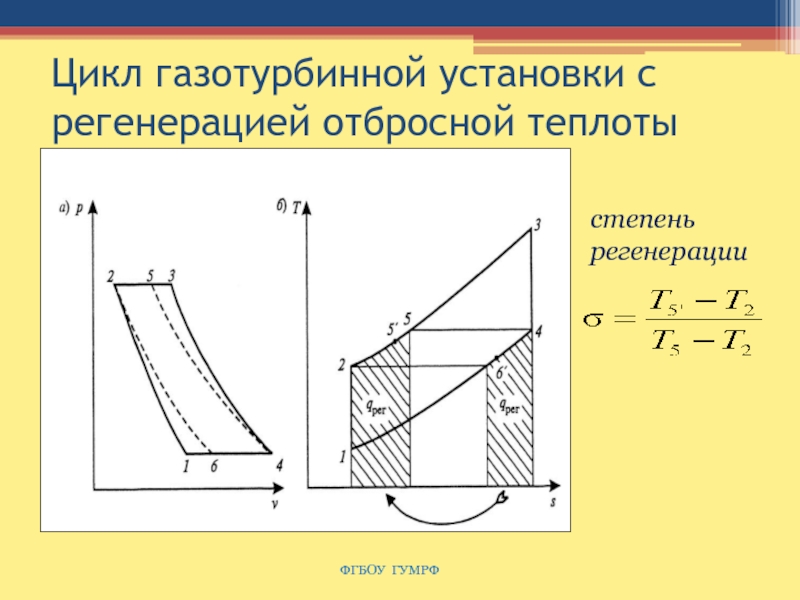
Слайд 68Цикл газотурбинной установки с регенерацией отбросной теплоты
ФГБОУ ГУМРФ
степень регенерации
Слайд 695.5. Компрессоры
где π = р2/р1 – степень повышения давления
ФГБОУ
ГУМРФ
Теоретический рабочий цикл в одноступенчатом поршневом компрессоре
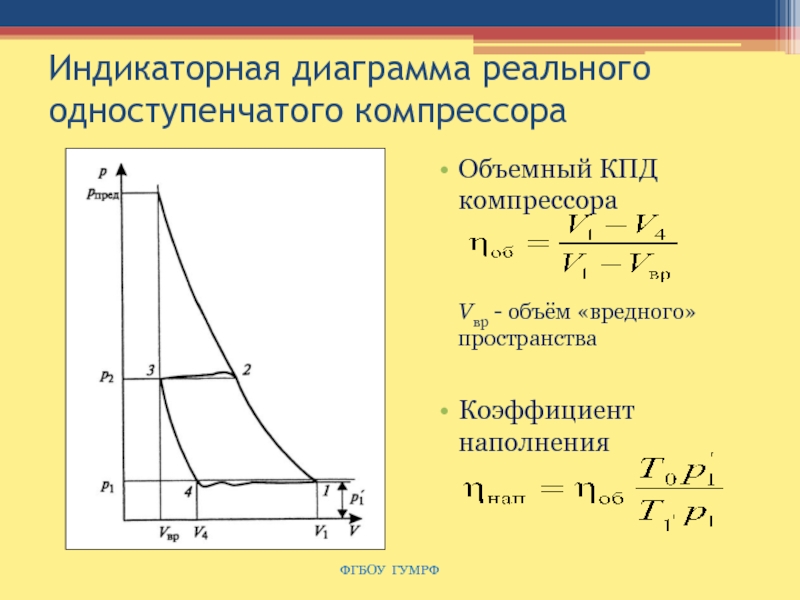
Слайд 70Индикаторная диаграмма реального одноступенчатого компрессора
Объемный КПД компрессора
Коэффициент наполнения
ФГБОУ ГУМРФ
Vвр
- объём «вредного» пространства
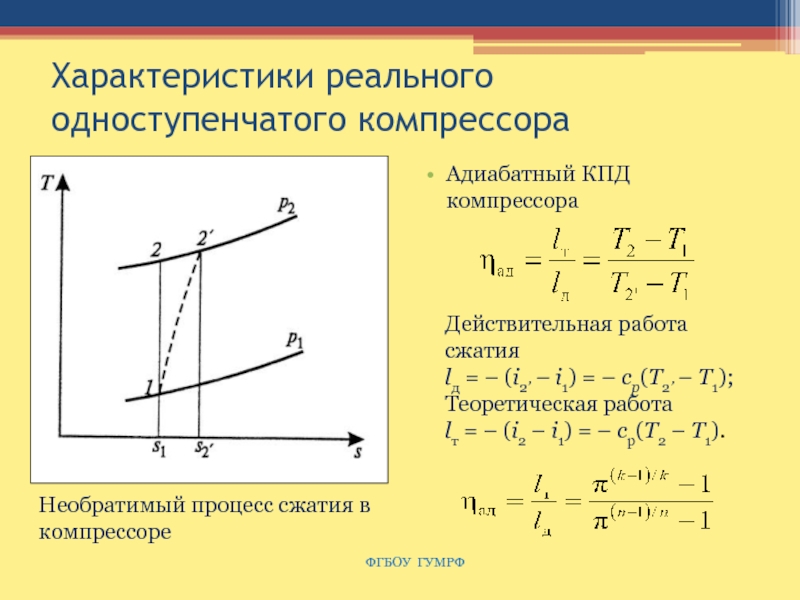
Слайд 71Характеристики реального одноступенчатого компрессора
Адиабатный КПД компрессора
ФГБОУ ГУМРФ
Необратимый процесс сжатия
в компрессоре
Действительная работа сжатия
lд = – (i2’ – i1) =
– cp(T2’ – T1);
Теоретическая работа
lт = – (i2 – i1) = – cp(T2 – T1).
Слайд 72Характеристики реального одноступенчатого компрессора
Реальная удельная работа цикла
Массовая производительность одного
цилиндра компрессора (кг/с)
где n – частота вращения вала компрессора,
об/мин.
Необходимая мощность привода компрессора , кВт
где ηмех – механический КПД компрессора
ФГБОУ ГУМРФ
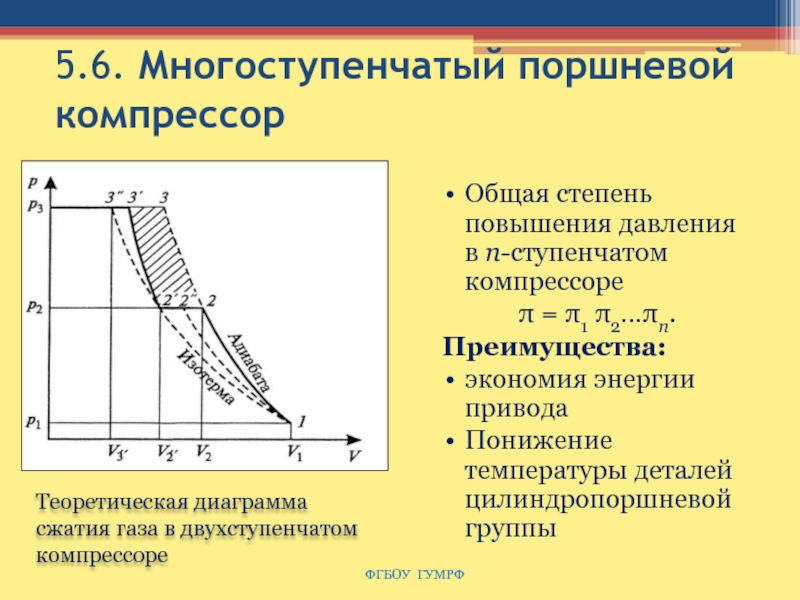
Слайд 735.6. Многоступенчатый поршневой компрессор
Общая степень повышения давления в n-ступенчатом компрессоре
π = π1 π2…πn.
Преимущества:
экономия энергии привода
Понижение температуры деталей цилиндропоршневой группы
ФГБОУ ГУМРФ
Теоретическая диаграмма сжатия газа в двухступенчатом компрессоре
Слайд 74Контрольные вопросы и задания к главе 5
Почему современные поршневые
двигатели внутреннего сгорания (ДВС) не проектируют на основе теоретического цикла
Карно?
Назвать основные безразмерные характеристики теоретических циклов поршневых ДВС.
Назвать три основных теоретических цикла поршневых ДВС.
Сравнить термические КПД трех теоретических циклов поршневых ДВС при одинаковой степени сжатия и одинаковых ограничениях по максимальному давлению и максимальной температуре цикла.
Как определить эффективный КПД реального теплового двигателя?
Как определить мощность на валу теплового двигателя?
Охарактеризовать теоретический цикл газотурбинной установки, определить его термический КПД.
ФГБОУ ГУМРФ
Слайд 75Контрольные вопросы и задания к главе 5
Определить термический КПД теоретического
цикла ГТУ с регенерацией отбросной теплоты.
Как можно регенерировать теплоту в
тепловом двигателе?
Представить теоретический «цикл» поршневого компрессора в осях р, υ.
Что называется степенью повышения давления в компрессоре?
Показать на графике отличие «цикла» реального поршневого компрессора от теоретического.
Что называется «вредным» пространством поршневого компрессора?
Что называется объемным КПД поршневого компрессора?
Что называется коэффициентом наполнения поршневого компрессора?
ФГБОУ ГУМРФ
Слайд 76
Глава 6.
РЕАЛЬНЫЙ ГАЗ. ФАЗОВЫЕ ПРЕВРАЩЕНИЯ
6.1. Уравнение Ван-дер-Ваальса.
Пограничные
кривые агрегатных состояний
ФГБОУ ГУМРФ
Слайд 77Реальный газ
Модель идеального газа не учитывает объем, занимаемый самими молекулами
газа, и силы притяжения между молекулами. Реальный газ сжимаем постольку,
поскольку в занимаемом им объеме есть пространство, не занятое его частицами.
Если удельный объем предельно упакованных частиц (b, м3/кг) сравнить с удельным объемом газа υ, то сжимаемая часть этого объема составит разность (υ – b).
ФГБОУ ГУМРФ
Слайд 78Реальный газ
Все частицы газа гравитационно взаимодействуют между собой.
Это взаимодействие
оказывается уравновешенным для всех частиц, за исключением находящихся в соприкосновении
со стенками вмещающего газ сосуда.
Эти частицы находятся под воздействием отрывающей их от стенки равнодействующей сил притяжения окружающими в полупространстве частицами газа.
От поверхности занимаемого газом объема эта сила направлена внутрь и создает в газе так называемое внутреннее давление, не воспринимаемое (не измеряемое) манометром.
ФГБОУ ГУМРФ
Слайд 79Уравнение Ван-дер-Ваальса
Учет внутреннего давления в уравнении состояния достигается прибавлением к
абсолютному давлению величины внутреннего давления.
(p + a/υ2) (υ – b)
= RT,
где a и b — определяемые эмпирически постоянные для данного газа.
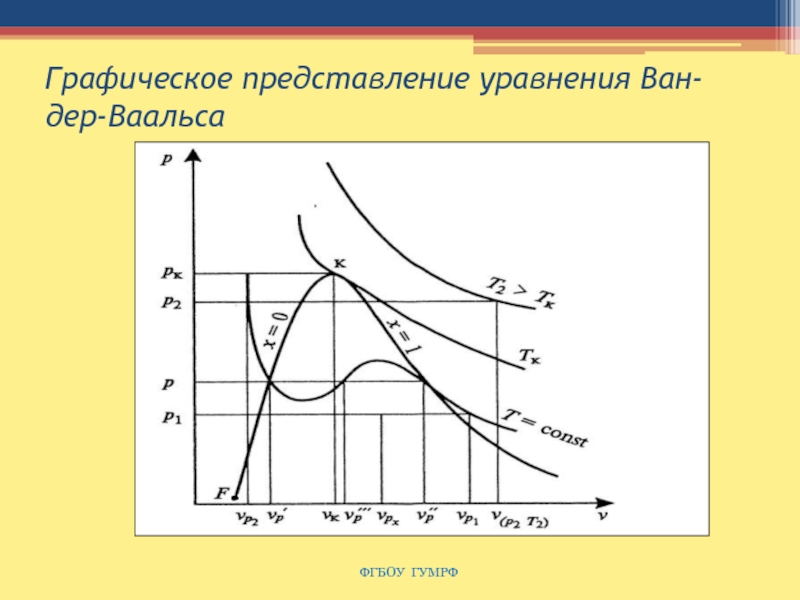
При фиксированных р и Т уравнение имеет либо один, либо три вещественных корня (υp', υp", υp"'),
т. е. изобара p = const пересекает кривую p = p(υ) в одной или трех точках.
ФГБОУ ГУМРФ
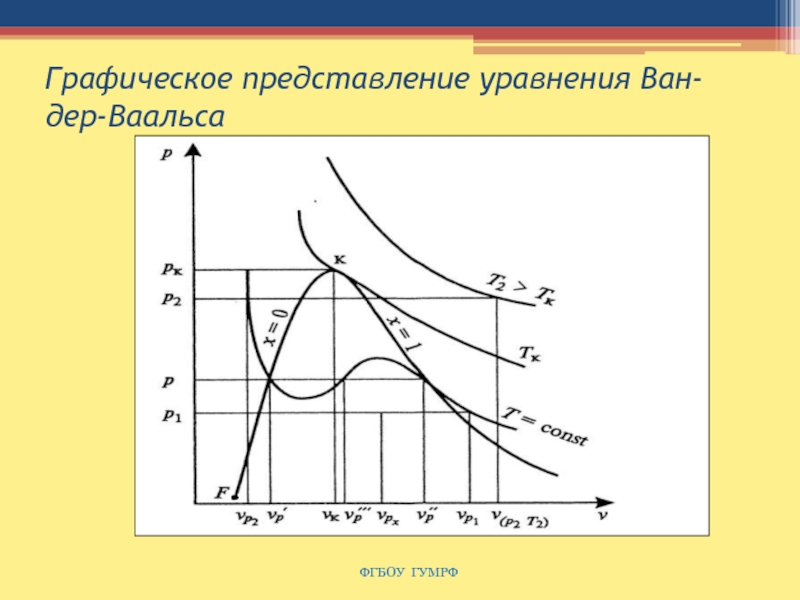
Слайд 80Графическое представление уравнения Ван-дер-Ваальса
ФГБОУ ГУМРФ
Слайд 81Пограничные кривые агрегатных состояний
При υp = υp" газ представляет собой сухой насыщенный
пар.
Точка υp = υp' соответствует жидкости в состоянии насыщения.
Между точками υp' и υp" газ
представляет собой двухфазную среду: смесь сухого насыщенного пара и жидкости.
Такая двухфазная смесь называется влажным паром.
ФГБОУ ГУМРФ
Слайд 82Пограничные кривые агрегатных состояний
Переход из газообразного состояния в жидкое через
двухфазное состояние (газ — жидкость) осуществляется по горизонтальной изотерме υp"–υp' при
постоянном давлении.
С повышением температуры газа Т сокращается и разность υp"–υp'. При некотором критическом сочетании температуры Тк и давления рк эта разность становится нулем (точка «к» на рисунке. ).
ФГБОУ ГУМРФ
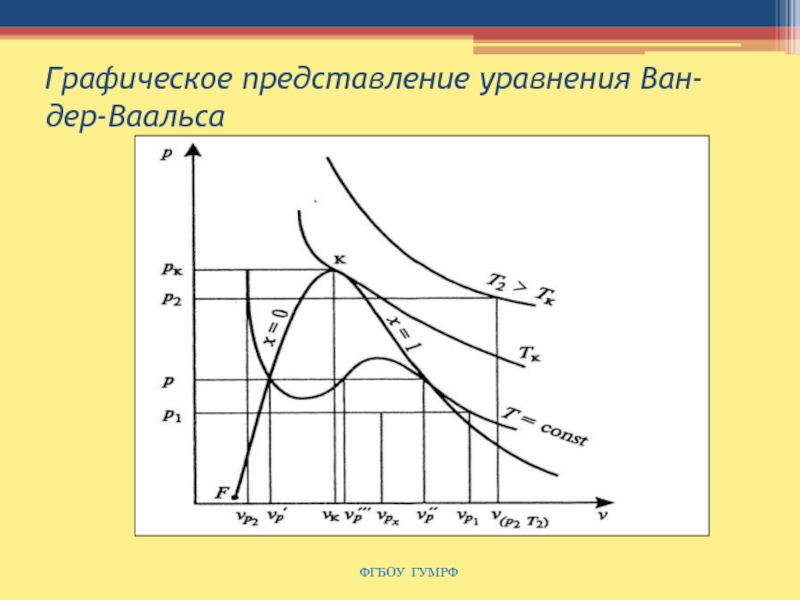
Слайд 83Графическое представление уравнения Ван-дер-Ваальса
ФГБОУ ГУМРФ
Слайд 84Пограничные кривые агрегатных состояний
Вещество в состоянии с параметрами υк, рк,
Тк утрачивает четко выраженные свойства жидкого или газообразного агрегатного состояния.
При таких критических параметрах газ переходит в жидкость и наоборот без теплообмена.
Точка с параметрами υк, рк, Тк называется двойной критической точкой.
ФГБОУ ГУМРФ
Слайд 85Пограничные кривые агрегатных состояний
Наличие критической точки на изотерме Ван-дер-Ваальса означает,
что для каждой жидкости существует такая температура, выше которой вещество
может существовать только в газообразном состоянии.
ФГБОУ ГУМРФ
Слайд 86Пограничные кривые агрегатных состояний
Непрерывная последовательность точек на диаграммах р–υ, T–s
и т. п., соответствующих состояниям начала конденсации (р–υ") и ее
конца (р–υ'), называется пограничной кривой.
ФГБОУ ГУМРФ
Слайд 87Пограничные кривые агрегатных состояний
Критическая точка «к» делит ее на нижнюю
(левую) пограничную кривую, точки которой изображают жидкость на линии насыщения
(х = 0), и верхнюю (правую) пограничную кривую, точки который изображают пар на лини насыщения (х = 1).
ФГБОУ ГУМРФ
Слайд 88Пограничные кривые агрегатных состояний
При параметрах слева от нижней пограничной кривой
рабочее тело находится в жидком состоянии, справа от верхней пограничной
кривой — в состоянии перегретого пара (или газа). Точки внутри пограничных кривых соответствуют различным состояниям влажного пара.
ФГБОУ ГУМРФ
Слайд 89Графическое представление уравнения Ван-дер-Ваальса
ФГБОУ ГУМРФ
Слайд 90Пограничные кривые агрегатных состояний
Переход в изобарном процессе с левой ветви
пограничной кривой на правую ветвь изображает процесс кипения, переход в
обратную сторону — процесс конденсации.
ФГБОУ ГУМРФ
Слайд 91Пограничные кривые агрегатных состояний
Нижняя пограничная кривая начинается в так называемой
фундаментальной или тройной критической точке (F).
Это точка с параметрам
pF, υF, TF, при которых три состояния вещества находятся в термодинамическом равновесии и переходят одно в другое без теплообмена. При этом υF' = υF" = b в уравнении Ван-дер-Ваальса.
ФГБОУ ГУМРФ
Слайд 926.2. Пар и его свойства
Состоянием насыщения называется такое состояние с
параметрами Ts, ps , при котором пар находится в термодинамическом
равновесии со своей жидкостью. В этом случае пар и его жидкость называются насыщенными.
Количество теплоты, необходимое для полного испарения 1 кг жидкости, называется удельной скрытой теплотой парообразования r (Дж/кг).
ФГБОУ ГУМРФ
Слайд 93Пар и его свойства
Сухой пар — это пар, не содержащий
капелек жидкости.
Влажный пар — это механическая смесь сухого насыщенного
пара и жидкости.
Относительное содержание в двухфазной смеси массы сухого насыщенного пара называется степенью сухости влажного пара:
x = mс.н.п/mсм.
Величина (1 – x) называется степенью влажности пара.
ФГБОУ ГУМРФ
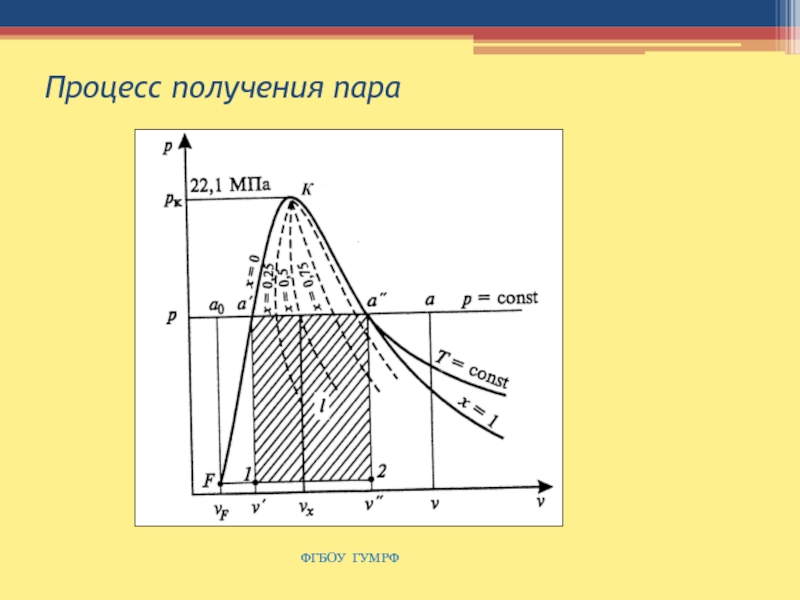
Слайд 94Параметры влажного пара
Удельный объём: υрx = xυp" + (1 –
x)υp'.
Энтальпия: ix = i'(1 – x) + i"x.
Внутренняя энергия
ux = u'(1 – x) + u"x.
Энтропия: sx = s'(1 – x) + s"x.
Параметры с одним штрихом относятся к жидкости на линии насыщения, а параметры с двумя штрихами — к пару на линии насыщения.
Если температура пара выше температуры насыщения при данном давлении, то такой пар называется перегретым
ФГБОУ ГУМРФ
Слайд 956.3. Термодинамические свойства воды и водяного пара
В фундаментальной (тройной критической)
точке вода имеет параметры:
pF = 0,00061 МПа; tF = 0,01 оС.
Для этого состояния полагают, что внутренняя энергия, энтальпия и энтропия воды равны нулю:
uF = 0; iF = 0; sF = 0.
В двойной критической точке «к» :
рк = 22,1 МПа; tк = 374 оС).
ФГБОУ ГУМРФ
Слайд 96Процесс получения пара
ФГБОУ ГУМРФ
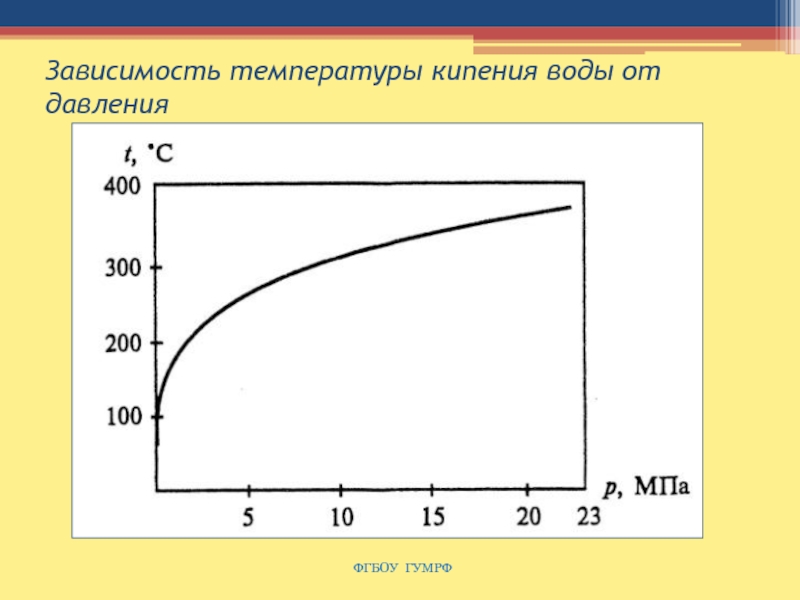
Слайд 97Зависимость температуры кипения воды от давления
ФГБОУ ГУМРФ
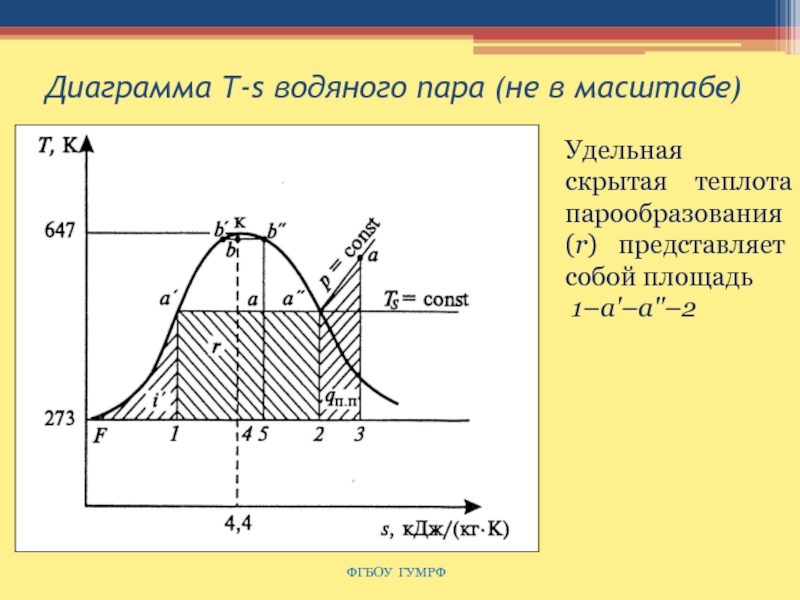
Слайд 98Диаграмма Т-s водяного пара (не в масштабе)
ФГБОУ ГУМРФ
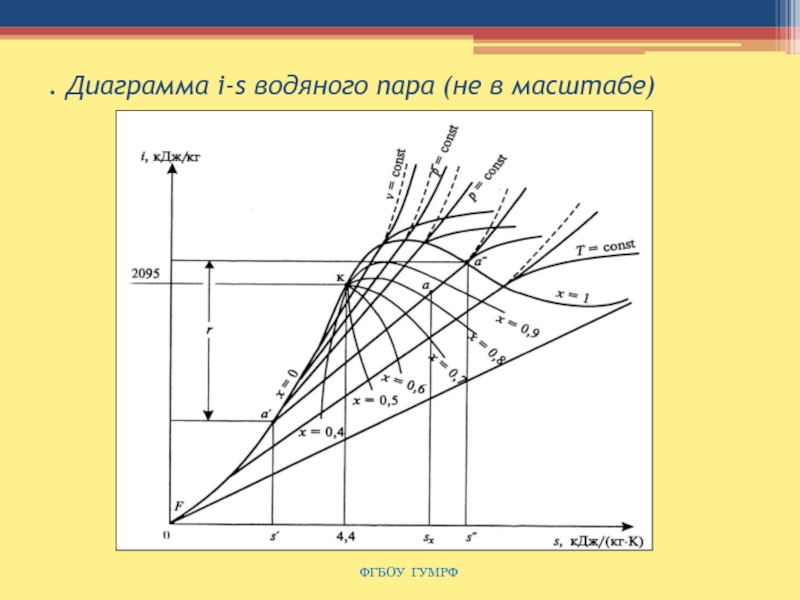
Удельная скрытая
теплота парообразования (r) представляет собой площадь
1–а'–а"–2
Слайд 99 Термодинамические свойства воды и водяного пара
Энтальпия сухого насыщенного пара,:
i"
= i' + r
Энтальпия перегретого пара :
ФГБОУ ГУМРФ
Энтропия перегретого
пара :
Слайд 100. Диаграмма i-s водяного пара (не в масштабе)
ФГБОУ ГУМРФ
Слайд 101Контрольные вопросы и задания к главе 6
Назвать основные отличия реального
газа от идеального.
Написать уравнение Ван-дер-Ваальса.
Определить пограничные кривые фазовых превращений.
Назвать фундаментальную и двойную критические точки воды, их параметры состояния.
Дать определение скрытой теплоты парообразования.
Дать описание термодинамических процессов на фоне пограничных кривых на осях р–υ, T–s и i–s.
ФГБОУ ГУМРФ
Слайд 102
Глава 7.
ЦИКЛЫ ПАРОТУРБИННЫХ УСТАНОВОК
7.1. ЦИКЛЫ ПАРОТУРБИННЫХ УСТАНОВОК.
Цикл Ренкина
ФГБОУ ГУМРФ
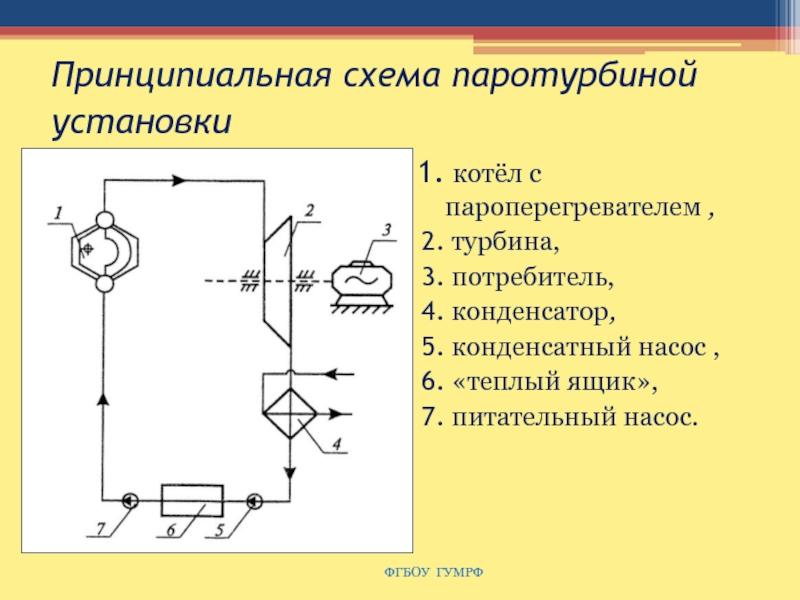
Слайд 103Принципиальная схема паротурбиной установки
котёл с пароперегревателем ,
турбина,
потребитель,
конденсатор,
конденсатный насос ,
«теплый ящик»,
питательный насос.
ФГБОУ
ГУМРФ
Слайд 104Циклы Ренкина в координатах Т–s
1–2 адиабатическое расширение пара в турбине
2–3 процесс конденсации пара 3-4 подогрев воды до температуры насыщения
4-5
испарение воды
5-1 перегрев пара.
ФГБОУ ГУМРФ
Слайд 1057.2. Влияние параметров пара на КПД цикла Ренкина
h = i1
– i2 полезная работа,
q 1 - количество подведённой теплоты.
Термический КПД
будет тем выше, чем выше давление и температура пара на входе в турбину (р1, Т1) и чем ниже давление в конденсаторе (р2).
ФГБОУ ГУМРФ
Слайд 106Влияние параметров пара на КПД цикла Ренкина
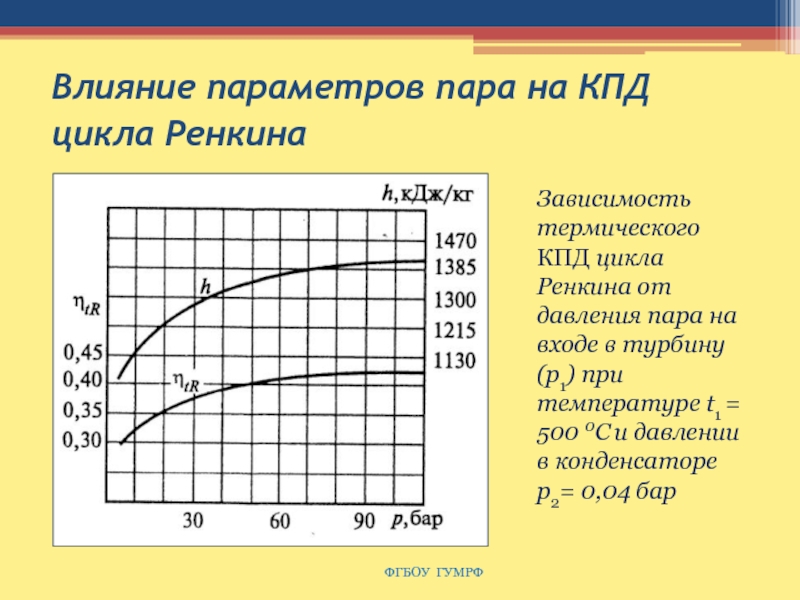
ФГБОУ ГУМРФ
Зависимость термического
КПД цикла Ренкина от давления пара на входе в турбину
(р1) при температуре t1 = 500 0C и давлении в конденсаторе р2= 0,04 бар
Слайд 107Влияние параметров пара на КПД цикла Ренкина
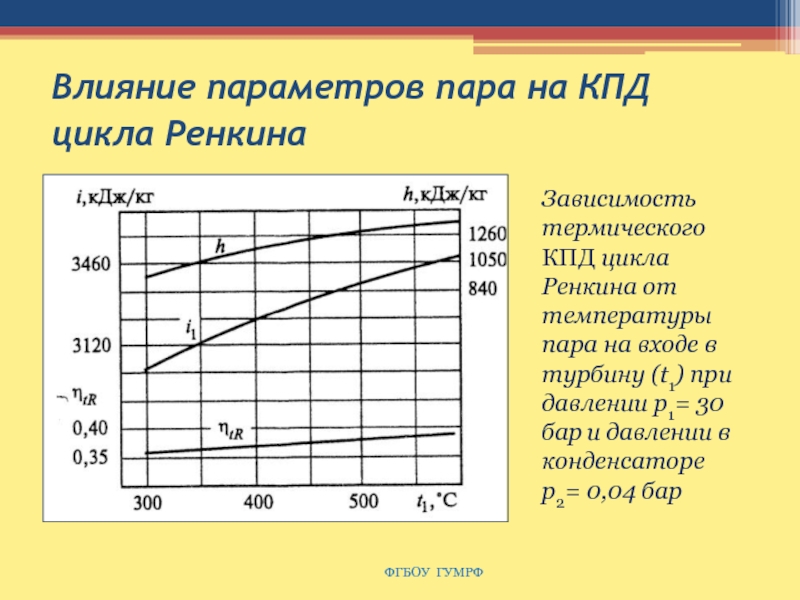
ФГБОУ ГУМРФ
Зависимость термического
КПД цикла Ренкина от температуры пара на входе в турбину
(t1) при давлении р1= 30 бар и давлении в конденсаторе р2= 0,04 бар
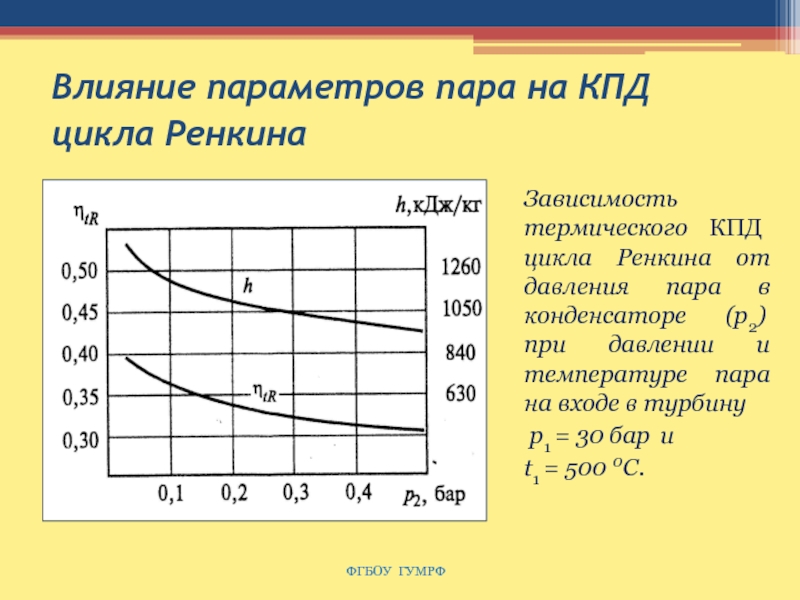
Слайд 108Влияние параметров пара на КПД цикла Ренкина
ФГБОУ ГУМРФ
Зависимость термического
КПД цикла Ренкина от давления пара в конденсаторе (р2) при
давлении и температуре пара на входе в турбину
р1 = 30 бар и
t1 = 500 0C.
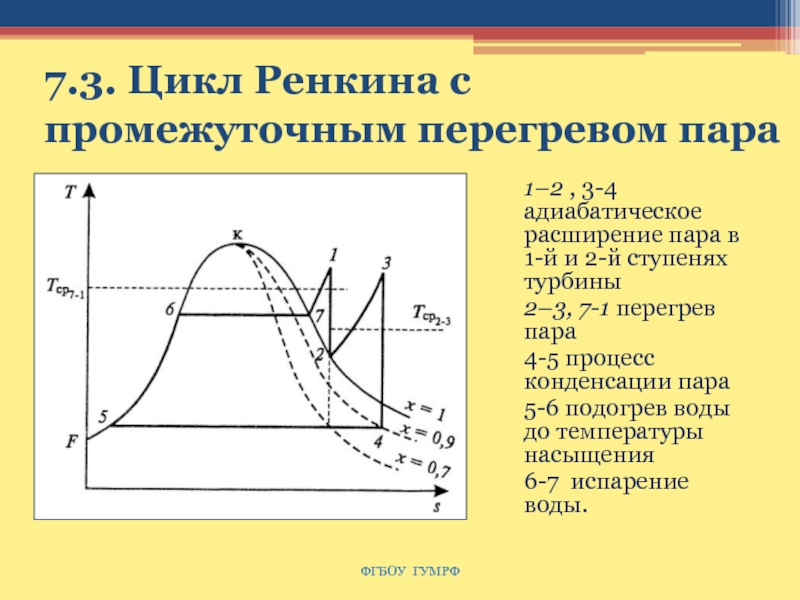
Слайд 1097.3. Цикл Ренкина с промежуточным перегревом пара
1–2 , 3-4 адиабатическое
расширение пара в 1-й и 2-й ступенях турбины
2–3, 7-1
перегрев пара
4-5 процесс конденсации пара
5-6 подогрев воды до температуры насыщения
6-7 испарение воды.
ФГБОУ ГУМРФ
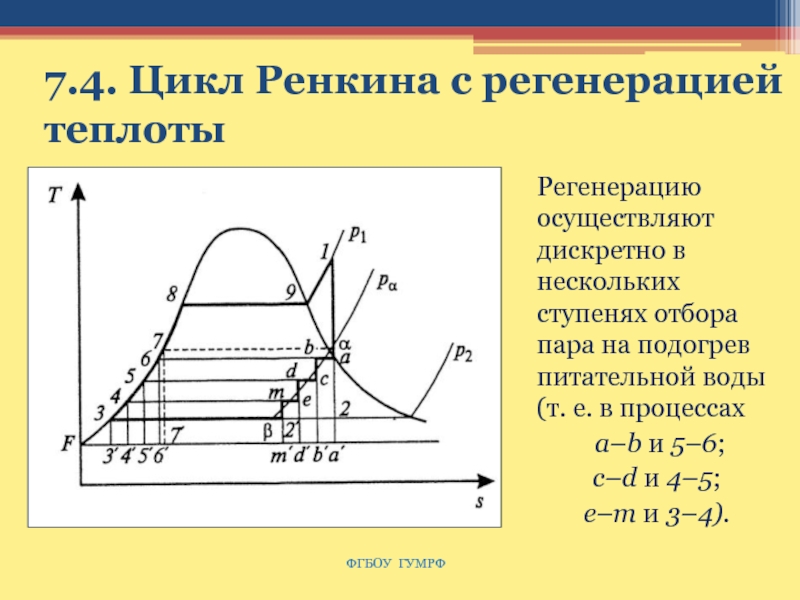
Слайд 1107.4. Цикл Ренкина с регенерацией теплоты
Регенерацию осуществляют дискретно в нескольких
ступенях отбора пара на подогрев питательной воды (т. е. в
процессах
a–b и 5–6;
c–d и 4–5;
e–m и 3–4).
ФГБОУ ГУМРФ
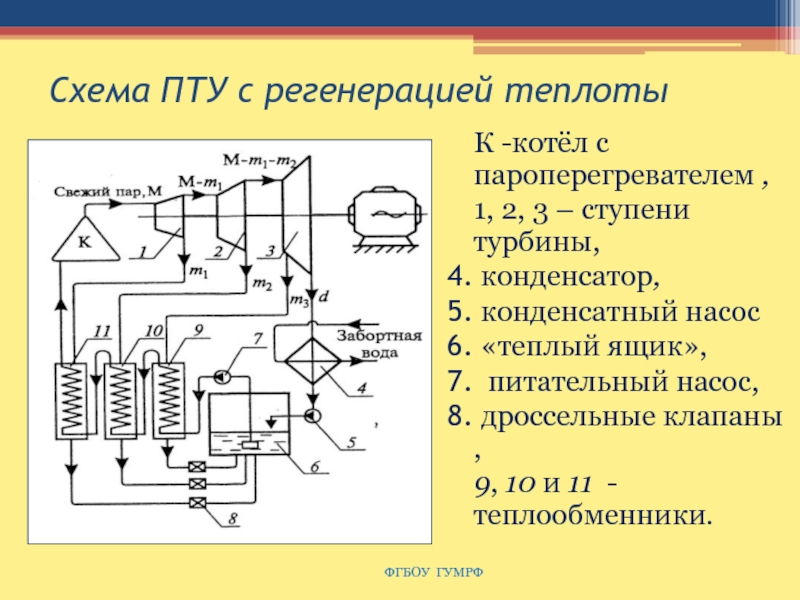
Слайд 111Схема ПТУ с регенерацией теплоты
К -котёл с пароперегревателем ,
1,
2, 3 – ступени турбины,
конденсатор,
конденсатный насос
«теплый ящик»,
питательный насос,
дроссельные клапаны ,
9, 10 и 11 - теплообменники.
ФГБОУ ГУМРФ
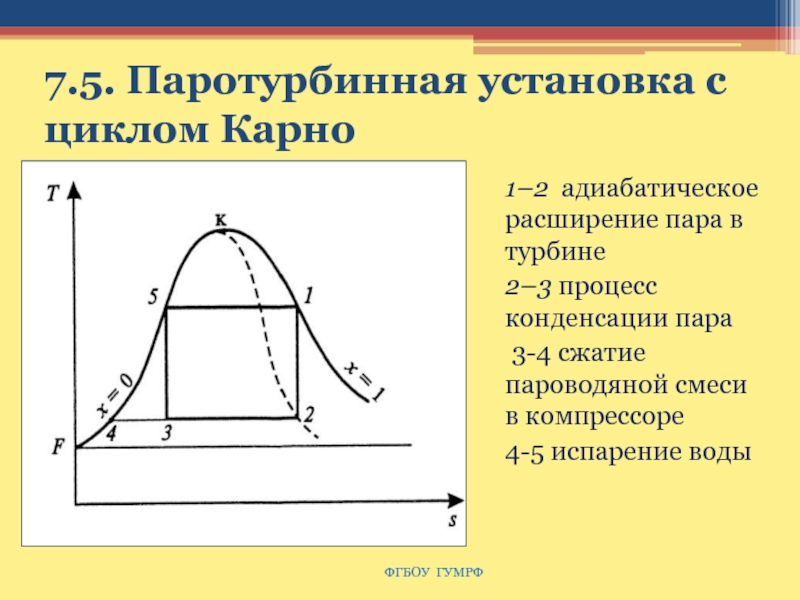
Слайд 1127.5. Паротурбинная установка с циклом Карно
1–2 адиабатическое расширение пара в
турбине
2–3 процесс конденсации пара
3-4 сжатие пароводяной смеси в
компрессоре
4-5 испарение воды
ФГБОУ ГУМРФ
Слайд 113Контрольные вопросы и задания к главе 7
1. Описать теоретический цикл
паротурбинной установки (ПТУ, цикл Ренкина) в координатах р–υ, T–s и
i–s.
2. Назвать модификации цикла Ренкина.
3. Указать влияние параметров пара на КПД цикла Ренкина.
4. Почему ПТУ не проектируются на основе теоретического цикла Карно?
ФГБОУ ГУМРФ
Слайд 114
Глава 8.
ТЕЧЕНИЕ УПРУГОЙ СРЕДЫ
8.1. Первый закон термодинамики для
потока упругой (сжимаемой) среды
ФГБОУ ГУМРФ
Под упругой средой понимают сжимаемую
жидкость, т. е. газ и пар.
Слайд 115 Первый закон термодинамики для потока упругой (сжимаемой) среды
Работа внешних
сил, приложенных к движущейся упругой среде, и притекающая к ней
извне теплота преобразуются в ее энергию.
Энергия движущейся упругой среды складывается из кинетической энергии видимого движения среды и ее внутренней энергии.
В расчете на 1 кг газа:
dq + dlsd + dlst = du + dk = cυdT + d(w2/2)
ФГБОУ ГУМРФ
Слайд 116 Первый закон термодинамики для потока упругой (сжимаемой) среды
В расчете
на 1 кг газа:
dq + dlsd + dlst = du
+ dk = cυdT + d(w2/2)
где dq — подведенное к 1 кг газа элементарное количество теплоты;
dlsd — элементарная работа поверхностных деформирующих сил, уравновешенных относительно центра тяжести выделенного объема газа;
dlst — элементарная работа транспортирующих поверхностных сил, , неуравновешенных относительно центра тяжести,
du = cυdT — элементарное изменение внутренней энергии выделенного объема;
d(w2/2) = dk — элементарное изменение кинетической энергии .
ФГБОУ ГУМРФ
Слайд 117 Первый закон термодинамики для потока упругой (сжимаемой) среды
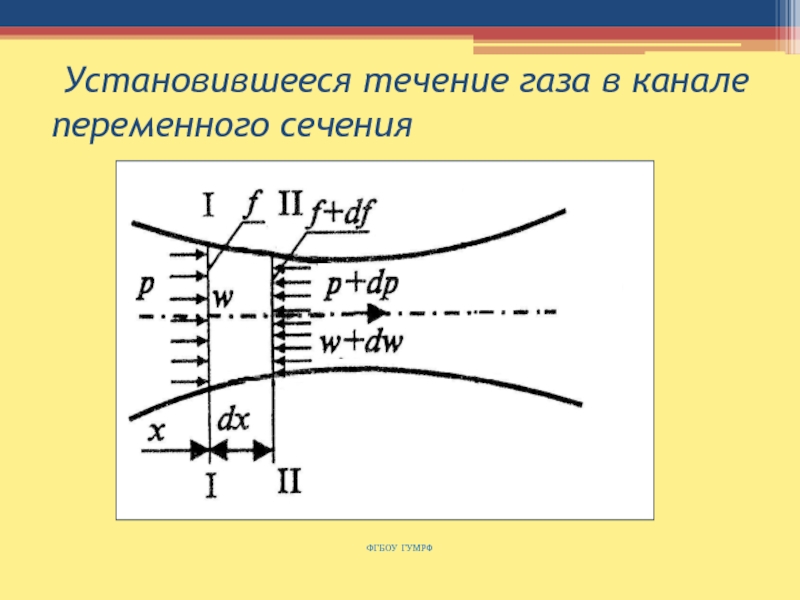
Рассмотрим сплошное,
стационарное течение упругой среды в прямом канале с произвольным изменением
по длине х площади поперечного сечения f.
Скорость движения в каждом сечении определяется из уравнения сплошности:
ФГБОУ ГУМРФ
где G, кг/с — массовый расход упругой среды, постоянный для всех сечений канала .
Слайд 118 Установившееся течение газа в канале переменного сечения
ФГБОУ ГУМРФ
Слайд 119 Первый закон термодинамики для потока упругой (сжимаемой) среды
В расчете
на 1 кг газа:
dq + dlsd + dlst = du
+ dk = cυdT + d(w2/2)
Без учета сил трения работа транспортирующих сил в расчете не на элементарную массу Gdτ:
d2Lst = pfwdτ – (p + dp) (f + df)(w + dw)dτ.
Произведя в правой части перемножение и отбросив величины высшего порядка малости, получим:
d 2Lst = –(pwdf + pfdw + fwdp)dτ = –[pd(fw) + fwdp]dτ
или с учетом условия сплошности (Gdυ = d(fw):
d 2Lst = –G(pdυ+ υdp)dτ = –Gd(pυ)dτ.
ФГБОУ ГУМРФ
Слайд 120 Первый закон термодинамики для потока упругой (сжимаемой) среды
В расчете
на 1 кг газа:
dq + dlsd + dlst = du
+ dk = cυdT + d(w2/2) (8.1)
Удельная работа транспортирующих сил, т. е. в расчете не на элементарную массу Gdτ, а на 1 кг рабочего тела:
dlst = –d(pυ).
Тогда уравнение (8.1) при отсутствии работы деформирующих сил (dlsd = 0) можно переписать:
dq = du + d(pυ) + d(w2/2) = di + d(w2/2). (8.2)
Математическая формулировка первого закона термодинамики для покоящегося газа имеет вид:
dq = du + pdυ. (8.3)
ФГБОУ ГУМРФ
Слайд 121 Первый закон термодинамики для потока упругой (сжимаемой) среды
dq =
du + d(pυ) + d(w2/2) = di + d(w2/2). (8.2)
Математическая
формулировка первого закона термодинамики для покоящегося газа имеет вид:
dq = du + pdυ. (8.3)
Если из левой и правой частей уравнения (8.2) вычесть соответствующие части уравнения (8.3), получим так называемое уравнение Д. Бернулли:
υdp + d(w2/2) = 0. (8.4)
Уравнения (8.3)…(8.4) представляют собой математические формулировки закона сохранения и превращения энергии.
ФГБОУ ГУМРФ
Слайд 1228.2. Скорость распространения звука в упругой среде.
Числа M и λ
Скоростью
звука называется скорость распространения малых возмущений в упругой среде.
Если
где-нибудь в потоке газа скорость станет равна местной скорости звука, то такая скорость газа w = aк называется критической; критическими будут называться и соответствующие значения давления, плотности и температуры: рк, ρк, Тк.
ФГБОУ ГУМРФ
Слайд 123Скорость распространения звука в упругой среде. Числа M и λ
Отношение
скорости w движения газа в данной точке потока к соответствующей
этой точке местной скорости звука , называется числом М (числом Маха).
ФГБОУ ГУМРФ
М < 1 – поток дозвуковой,
М > 1 – поток сверхзвуковой.
Слайд 124Скорость распространения звука в упругой среде. Числа M и λ
Отношение
скорости потока в данной точке к одинаковой для всего потока
в целом критической скорости w/aк = λ будем называть скоростным коэффициентом.
ФГБОУ ГУМРФ
скорость распространения звука
– скорость звука в идеальном газе
Слайд 1258.3. Движение газа в прямом канале переменного сечения
ФГБОУ ГУМРФ
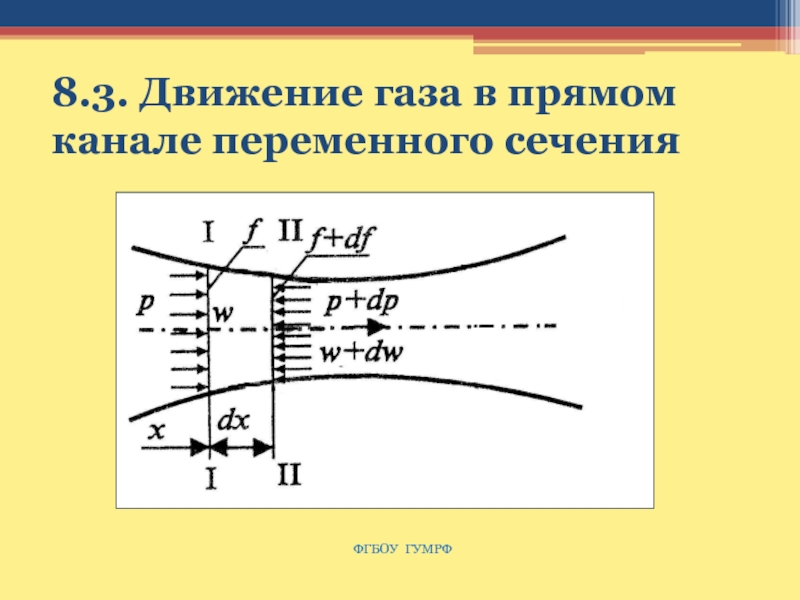
Слайд 126 Движение газа в прямом канале переменного сечения
Скорость движения в
каждом сечении определяется из уравнения сплошности:
ФГБОУ ГУМРФ
Продифференцируем уравнение сплошности
:
fdw + wdf = Gdυ и разделим результат на fw = Gυ:
(8.5)
Слайд 127 Движение газа в прямом канале переменного сечения
Полагаем, что в
процессе течения в канале параметры газа изменяются адиабатически: pυk =
const.
Отсюда после дифференцирования и разделения членов левой части на pυk находим:
ФГБОУ ГУМРФ
Из уравнения Бернулли:
(8.6)
(8.7)
Слайд 128 Движение газа в прямом канале переменного сечения
Подставляя выражения (8.6)
и (8.7) в (8.5) , получим:
ФГБОУ ГУМРФ
- скорость звука
(8.8)
Течение
с нарастающей скоростью возможно в направлении понижающегося давления (dp < 0), при этом пока w < а, площадь сечения канала также должна уменьшаться (df < 0).
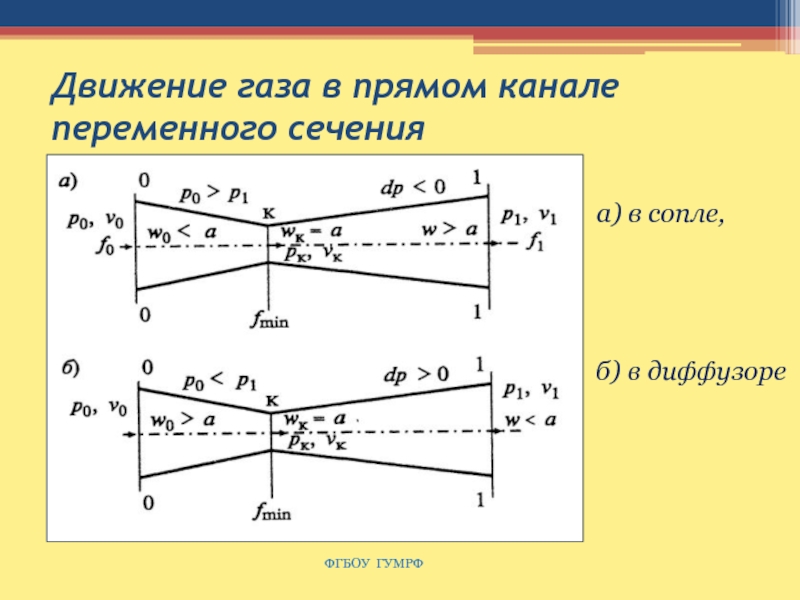
Слайд 129Движение газа в прямом канале переменного сечения
ФГБОУ ГУМРФ
а) в
сопле,
б) в диффузоре
Слайд 130 Движение газа в прямом канале переменного сечения
ФГБОУ ГУМРФ
Для
дальнейшего увеличения скорости течения в канале площадь его сечения теперь
должна нарастать:
dp < 0 →df > 0 в соответствии с уравнением (8.8)
(8.8)
В минимальном сечении скорость потока достигает критического значения, равного скорости звука:
Слайд 131 Движение газа в прямом канале переменного сечения
ФГБОУ ГУМРФ
Канал,
по которому газ движется в направлении понижающегося давления с нарастающей
скоростью, называется соплом.
Для достижения потоком сверхзвуковой скорости сопло должно быть сначала суживающимся, а затем расширяющимся (комбинированное сопло Лаваля). В сечении
f = fmin достигается критическая скорость течения, равная скорости звука в текущем газе при параметрах его состояния именно в этом сечении.
Слайд 132 Движение газа в прямом канале переменного сечения
ФГБОУ ГУМРФ
Канал,
по которому газ движется в направлении повышающегося давления с понижающейся
скоростью, называется диффузором.
В нем кинетическая энергия потока преобразуется в потенциальную энергию повышенного давления.
Скорость сверхзвукового потока в сечении f = fmin падает до критического значения, равного скорости звука в текущем газе при параметрах его состояния именно в этом сечении.
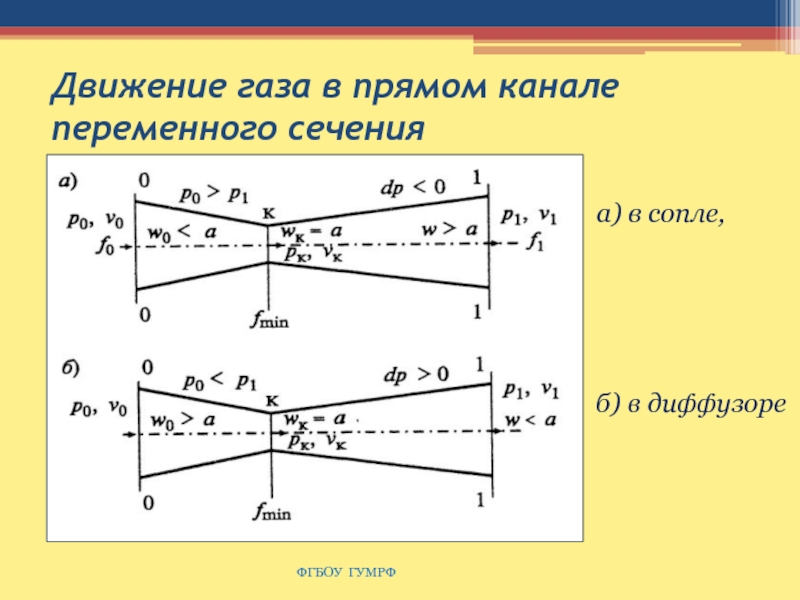
Слайд 133Движение газа в прямом канале переменного сечения
ФГБОУ ГУМРФ
а) в
сопле,
б) в диффузоре
Слайд 1348.4. Зависимость скорости истечения газа от перепада давления
ФГБОУ ГУМРФ
1-й
закон термодинамики:
dq = du + d(pυ) + d(w2/2) =
= di
+ d(w2/2) (8.3)
Проинтегрируем уравнение с учётом dq = 0 и w0= 0:
Слайд 135 Зависимость скорости истечения газа от перепада давления
ФГБОУ ГУМРФ
Проинтегрируем
уравнение Бернулли
υdp + d(w2/2) = 0 :
с учётом w0= 0
и
, получим:
, где β = р/р0.
Слайд 136 Зависимость скорости истечения газа от перепада давления
ФГБОУ ГУМРФ
Когда
газ истекает в вакуум (β = 0) :
Определим отношение давления
βк, при котором скорость истечения достигает критического значения wк=
Слайд 137 Зависимость скорости истечения газа от перепада давления
ФГБОУ ГУМРФ
Откуда
критическое отношение давлений :
Критическая скорость истечения:
где =
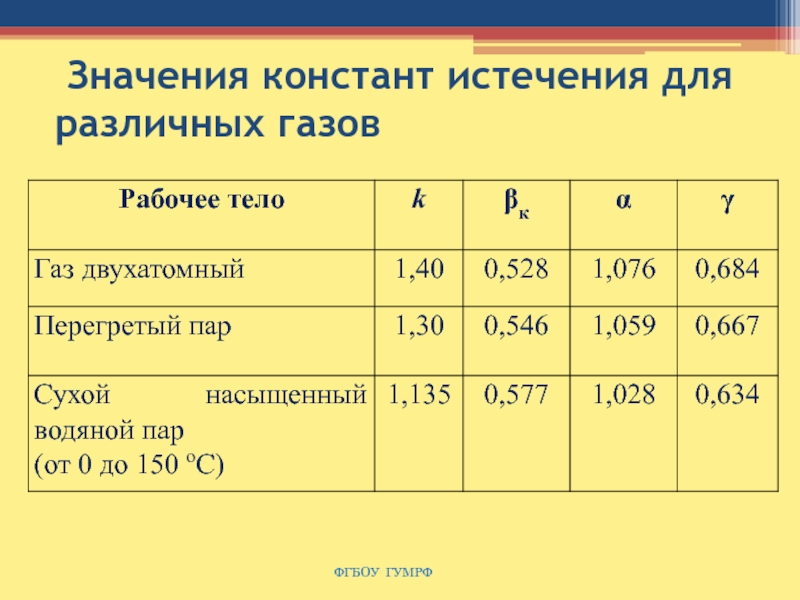
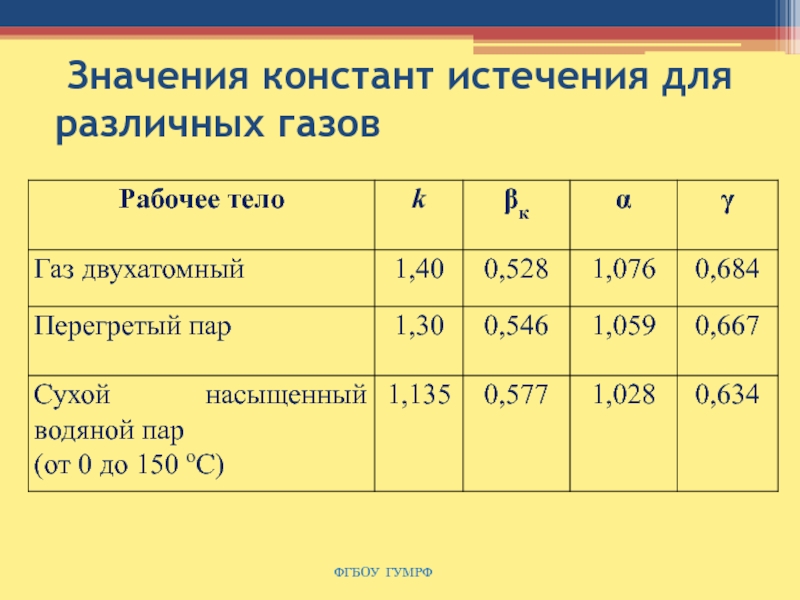
Слайд 138 Значения констант истечения для различных газов
ФГБОУ ГУМРФ
Слайд 1398.5. Расход газа при истечении из резервуара
ФГБОУ ГУМРФ
Расход G,
(кг/с) определится из уравнения сплошности:
С учётом уравнения адиабаты:
получим:
Слайд 140 Расход газа при истечении из резервуара
ФГБОУ ГУМРФ
При достижении
β=βк и критической скорости истечения расход газа достигает максимального значения
и с дальнейшим уменьшением β не возрастает. Это относится и к истечению газа из Сопла Лаваля (иначе нарушается уравнение сплошности).
Следовательно, максимальный расход газа :
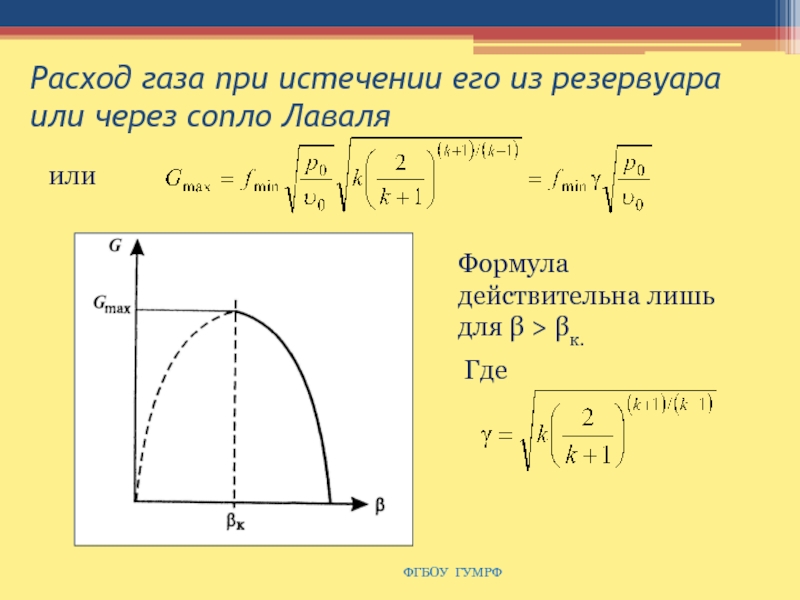
Слайд 141Расход газа при истечении его из резервуара или через сопло
Лаваля
ФГБОУ ГУМРФ
или
Где
Формула действительна лишь для β > βк.
Слайд 142 Значения констант истечения для различных газов
ФГБОУ ГУМРФ
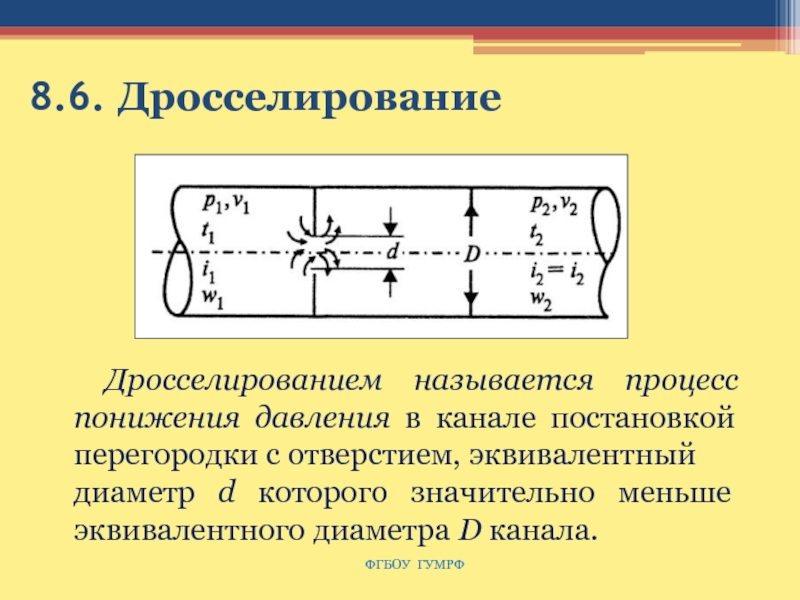
Слайд 1438.6. Дросселирование
ФГБОУ ГУМРФ
Дросселированием называется процесс понижения давления в канале
постановкой перегородки с отверстием, эквивалентный
диаметр d которого значительно меньше
эквивалентного диаметра D канала.
Слайд 144Дросселирование
ФГБОУ ГУМРФ
w1 = w2, Т1≈Т2 , р1υ1 = р2υ2
i =
const
Слайд 145Контрольные вопросы и задания к главе 8
1. Сформулировать и написать
уравнение первого закона термодинамики для потока упругой среды.
2. Каким должен
быть канал, скорость течения газа в котором может превысить звуковую?
3. Как определить скорость звука в газе с определенными параметрами состояния?
4. Как определить скорость истечения газа через насадку из резервуара большого объема?
5. Что называется соплом и диффузором?
ФГБОУ ГУМРФ
Слайд 146Контрольные вопросы и задания к главе 8
6. Что называется критическим
отношением давлений при истечении газа из резервуара и как оно
определяется?
7. Как определяется расход газа при истечении его через насадку из резервуара большого объема?
8. Как определяется действительная скорость газа при истечении его через насадку из резервуара большого объема?
9. Что представляет собой процесс дросселирования?
ФГБОУ ГУМРФ
Слайд 147
Глава 9.
ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ ХОЛОДИЛЬНЫХ УСТАНОВОК
9.1. Обратный цикл Карно
ФГБОУ ГУМРФ
Цикл холодильной установки является обращенным циклом теплового двигателя (т. е.
развивающимся против часовой стрелки).
Слайд 148 Обратный цикл Карно
ФГБОУ ГУМРФ
И –испаритель
КМ – компрессор
РЦ-расширительный цилиндр
КД – конденсатор
влажный насыщенный пар при температуре Т1
сухой насыщенный
пар при температуре Т2
жидкость при температуре Т2
двухфазная смесь при температуре Т1
Слайд 149 Обратный цикл Карно
ФГБОУ ГУМРФ
1-2 – адиабата сжатия
2-3 -
конденсация
3-4 – адиабата расширения
4-1 -испарение
Влажный пар при температуре Т1
сухой
насыщенный пар при температуре Т2
жидкость при температуре Т2
двухфазная смесь при температуре Т1
Слайд 150 Обратный цикл Карно
ФГБОУ ГУМРФ
Количество теплоты q0, отводимое от
охлаждаемого объекта единицей массы хладагента, называется его удельной массовой холодопроизводительностью:
q0
= i1 – i4 = r1(x1 – x4)
где r1 — удельная теплота парообразования при температуре T0= T4= T1.
Удельное количество теплоты, отводимое в конденсаторе : qк = i2 – i3 = r2
Удельная работа l0, затрачиваемая на адиабатное сжатие 1 кг паров холодильного агента: l0 = i2 – i1.
Полезная работа, совершаемая расширительным цилиндром : lРЦ = i3 – i4.
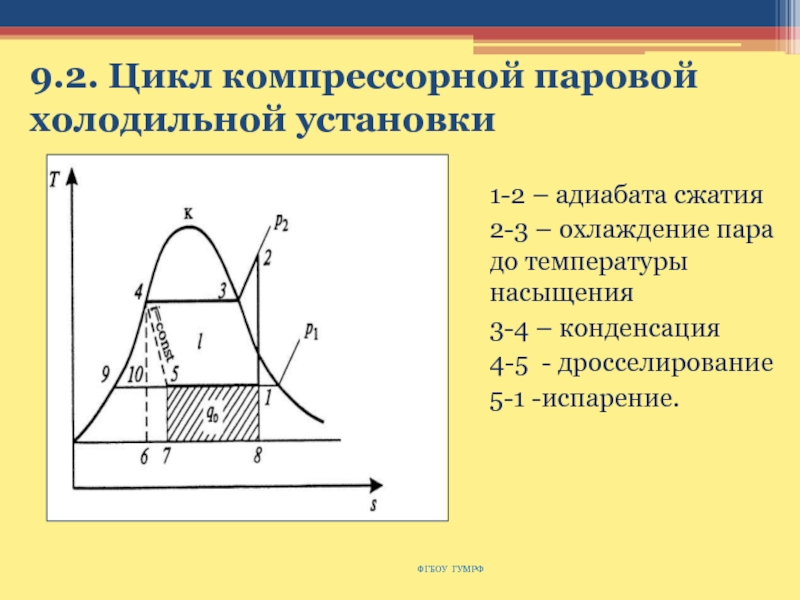
Слайд 1529.2. Цикл компрессорной паровой холодильной установки
ФГБОУ ГУМРФ
1-2 – адиабата
сжатия
2-3 – охлаждение пара до температуры насыщения
3-4 – конденсация
4-5 -
дросселирование
5-1 -испарение.
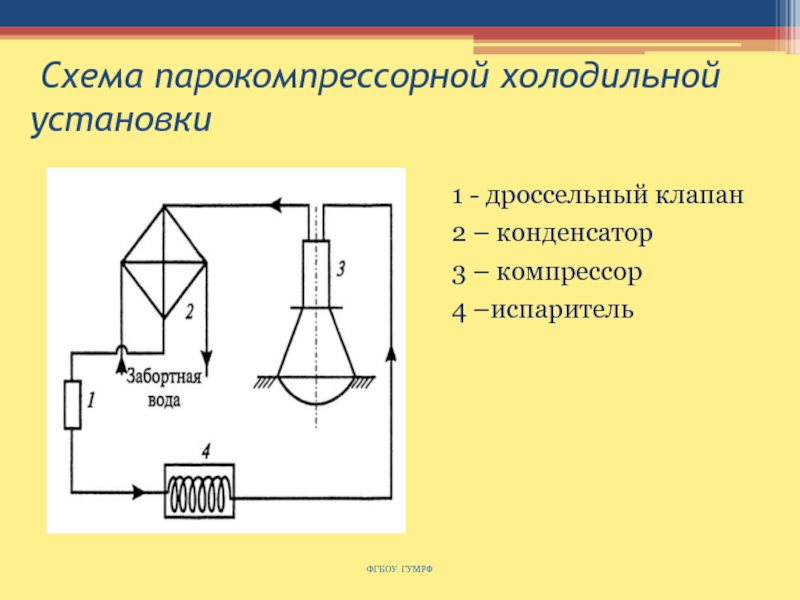
Слайд 153 Схема парокомпрессорной холодильной установки
ФГБОУ ГУМРФ
1 - дроссельный клапан
2 – конденсатор
3 – компрессор
4 –испаритель
Слайд 154 Цикл компрессорной паровой холодильной установки
ФГБОУ ГУМРФ
Удельная холодопроизводительность: q0 = i1
– i5
Удельное количество теплоты, отводимое в конденсаторе : qk = i2
– i4
Удельная работа l0, затрачиваемая на адиабатное сжатие 1 кг паров в компрессоре: lц = i2 – i1.
Холодильный коэффициент установки:
Дросселирование (процесс 4–5) снижает эффективность холодильной установки, однако позволяет регулировать режим её работы.
Слайд 155Контрольные вопросы и задания к главе 9
1. Что представляет
собой обратный цикл Карно и в какой схеме установки он
может быть реализован?
2. Описать цикл компрессорной паровой холодильной установки, нарисовать ее схему.
3. Что называется холодильным коэффициентом и холодопроизводительностью холодильной установки?
4. Какие рабочие тела используются в современных холодильных установках и каким требованиям они должны удовлетворять?
5. Как маркируются фреоны?
6. Назвать преимущества и недостатки фреонов как рабочего тела в холодильных установках.
ФГБОУ ГУМРФ
Слайд 156
Глава 10.
ГАЗОВЫЕ СМЕСИ
10.1. Термодинамические характеристики газовых смесей
ФГБОУ ГУМРФ
Газовой
смесью называется смесь газов, компоненты которых не вступают в химические
реакции.
Закон Дальтона:
рс = р1 + р2 +…+рn
где рс — давление смеси; р1, р2,…, рn — парциальные давления каждого из газов, входящих в смесь.
Слайд 157 Термодинамические характеристики газовых смесей
ФГБОУ ГУМРФ
Каждый из входящих в
смесь объемом Vс газов занимает весь объем со своим парциальным
давлением, и для него справедливо уравнение состояния:
piVc = МiRiTc,
где Мi — массовое содержание i-го газа в смеси; Ri — газовая постоянная этого газа.
Уравнение состояния смеси:
рсVc = МcRcTc
Слайд 158 Термодинамические характеристики газовых смесей
ФГБОУ ГУМРФ
Масса смеси:
Газовая постоянная
смеси:
где mi = Mi/Mc — массовая доля каждого компонента в
смеси газов.
Парциальное давление:
Относительный парциальный объем : ri = Vi/Vc, тогда по уравнению Бойля—Мариотта (при Т = Тс): pi = ripc.
Мольная доля газа: vi = ni/nc,
Слайд 159 Термодинамические характеристики газовых смесей
ФГБОУ ГУМРФ
Объемы одного моля Vμ
всех газов при одинаковых давлении и температуре одинаковы.
Поэтому относительное
мольное содержание i-го газа в смеси равно его относительному объемному содержанию:
Молекулярная масса смеси:
Массовая теплоемкость смеси
Слайд 16010.2. Атмосферный воздух как газовая смесь
ФГБОУ ГУМРФ
Влажный воздух рассматривают
как газовую смесь сухого воздуха и пара: р = рс.в.
+ рп.
Абсолютной влажностью называется массовое содержание пара в 1 м3 воздуха. Численно она равна плотности пара ρп при парциальном давлении рп.
Относительной влажностью называется отношение абсолютной влажности ненасыщенного воздуха к его максимальной абсолютной влажности при той же температуре:
кг/кмоль.
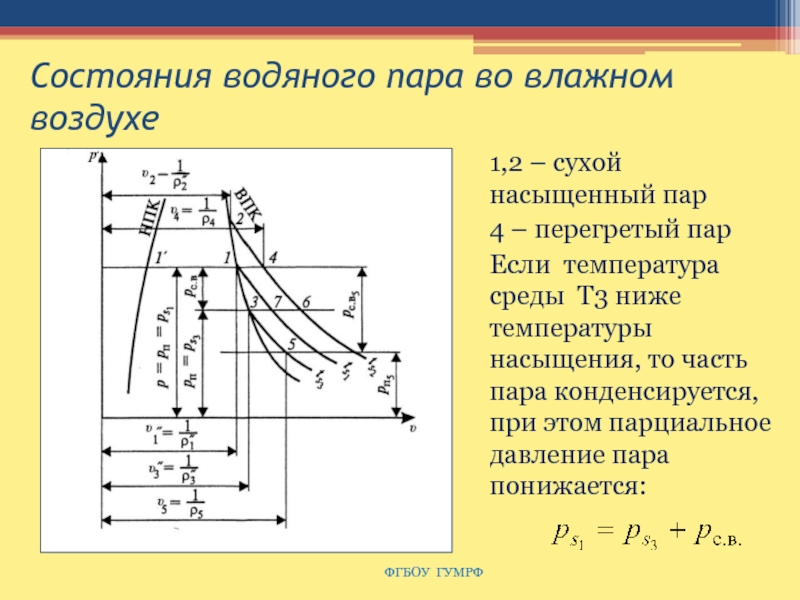
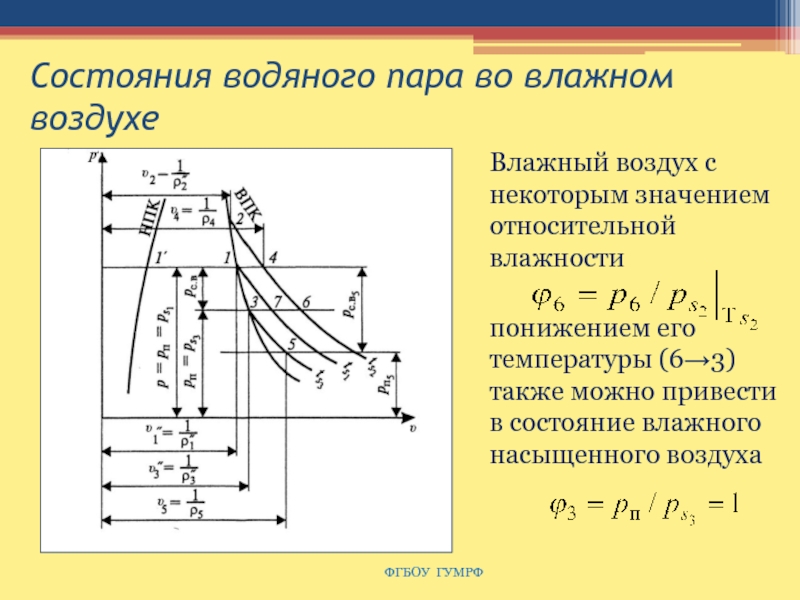
Слайд 161Состояния водяного пара во влажном воздухе
ФГБОУ ГУМРФ
1,2 – сухой
насыщенный пар
4 – перегретый пар
Если температура среды Т3 ниже температуры
насыщения, то часть пара конденсируется, при этом парциальное давление пара понижается:
Слайд 162Состояния водяного пара во влажном воздухе
ФГБОУ ГУМРФ
Абсолютная влажность зависит
не от общего давления в среде (р), а от парциального
давления пара (рп) и температуры.
При определенной температуре максимальная абсолютная влажность достигается при парциальном давлении пара, равном давлению насыщения, соответствующему данной температуре (точки 1, 2, 3).
Если при этом общее давление среды:
р = рп = ps - сухой насыщенный пар
р = рп < ps – перегретый пар
р = рп + pс.в – влажный воздух.
Слайд 163Состояния водяного пара во влажном воздухе
ФГБОУ ГУМРФ
Если общее давление
среды р больше парциального давления пара рп , и парциальное
давление пара при этом равно давлению насыщения при температуре среды, последнюю называют насыщенным влажным воздухом.
Насыщенный влажный воздух имеет максимальную (при данной температуре) абсолютную влажность.
Относительной влажностью называется отношение абсолютной влажности ненасыщенного воздуха к его максимальной абсолютной влажности при той же температуре:
Слайд 164Состояния водяного пара во влажном воздухе
ФГБОУ ГУМРФ
Влажный воздух с
некоторым значением относительной влажности
понижением его температуры (6→3) также
можно привести в состояние влажного насыщенного воздуха
Слайд 165Состояния водяного пара во влажном воздухе
ФГБОУ ГУМРФ
Состояние, при котором
парциальное давление пара равно давлению насыщения, соответствующему температуре влажного воздуха,
называется точкой росы, а температура, при которой наступает это состояние называется температурой точки росы (T3=Ts3 ).
Влагосодержанием воздуха d называют массу пара, приходящуюся на 1 кг сухого воздуха или на (1 + d) кг влажного воздуха.
Для некоторого объема V влажного воздуха:
Слайд 166Состояния водяного пара во влажном воздухе
ФГБОУ ГУМРФ
Разделим почленно одно
на другое два уравнения состояния для массы сухого воздуха mс.в.
и водного пара mп, входящих в объем V влажного воздуха:
Отсюда с учетом pс.в =р – рп , получим:
Следовательно, с увеличением парциального давления пара влагосодержание воздуха увеличивается.
Слайд 16710.3. Способы определения относительной влажности. Диаграмма i–d
ФГБОУ ГУМРФ
Металлический тонкостенный
цилиндр, заполненный эфиром, прокачивается воздухом. Часть эфира при этом испаряется,
что понижает его температуру.
Температура, при которой на наружной поверхности цилиндра появляется роса, является температурой точки росы для окружающего гигрометр влажного воздуха.
Гигрометр
Слайд 168Гигрометр
ФГБОУ ГУМРФ
На р–υ-диаграмме отмечаются точки (7 — по термометру
в воздухе и 3 — по термометру в эфире), полностью
определяющие все характеристики влажного воздуха: рп; рп + pс.в = р (по барометру); ρ7;
Слайд 169Психрометр
ФГБОУ ГУМРФ
Психрометр состоит из двух термометров: сухого и смоченного.
Головка с ртутью смоченного термометра обернута тонким слоем ткани, к
которой по фитилю непрерывно поступает вода. Влажность определяется по разности показаний сухого и смоченного термометров. Если влажный воздух не насыщен, вода с поверхности ткани испаряется и смоченный термометр показывает более низкую температуру, чем сухой.
Характеристики влажного воздуха определяются аналогично предыдущему случаю.
Слайд 170Характеристики влажного воздуха
ФГБОУ ГУМРФ
Газовая постоянная влажного воздуха
где rс.в.и rп
— объемные доли сухого воздуха и пара соответственно; μс.в. и
μп — молекулярные массы сухого воздуха (29 кг/кмоль) и пара (18 кг/кмоль) соответственно.
Энтальпия (1 + d) кг влажного воздуха: i = iс.в. + d iп.
Или: i = t + (2500 + 2ts)d.
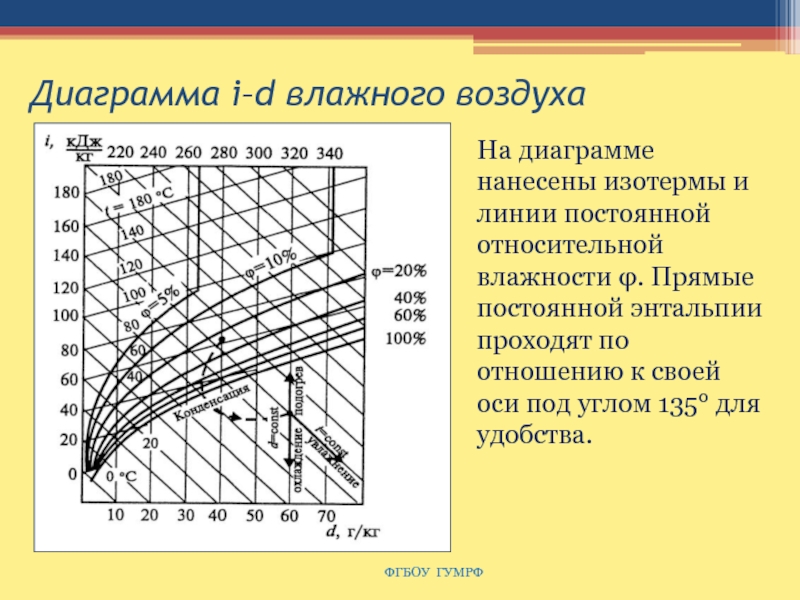
Слайд 171Диаграмма i–d влажного воздуха
ФГБОУ ГУМРФ
На диаграмме нанесены изотермы и
линии постоянной относительной влажности φ. Прямые постоянной энтальпии проходят по
отношению к своей оси под углом 135° для удобства.
Слайд 172Контрольные вопросы и задания к главе 10
1. Что называется
газовой смесью в технической термодинамике?
2. Сформулировать закон Дальтона для газовых
смесей.
3. Что представляет собой атмосферный воздух как газовая смесь?
4. Что называется абсолютной влажностью, относительной влажностью, влагосодержанием атмосферного воздуха?
5. Какое состояние называется «точкой росы»?
6. Как определяется энтальпия атмосферного воздуха?
7. Назвать основные термодинамические процессы в атмосферном воздухе в диаграмме i–d.
8. Описать практические способы определения относительной влажности атмосферного воздуха.
ФГБОУ ГУМРФ