Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проектирование последовательных схем
Содержание
- 1. Проектирование последовательных схем
- 2. Конечные автоматыВ реальных последовательных схемах существует конечное
- 3. Модели синхронных последовательных схемСуществуют две различные модели:Модель
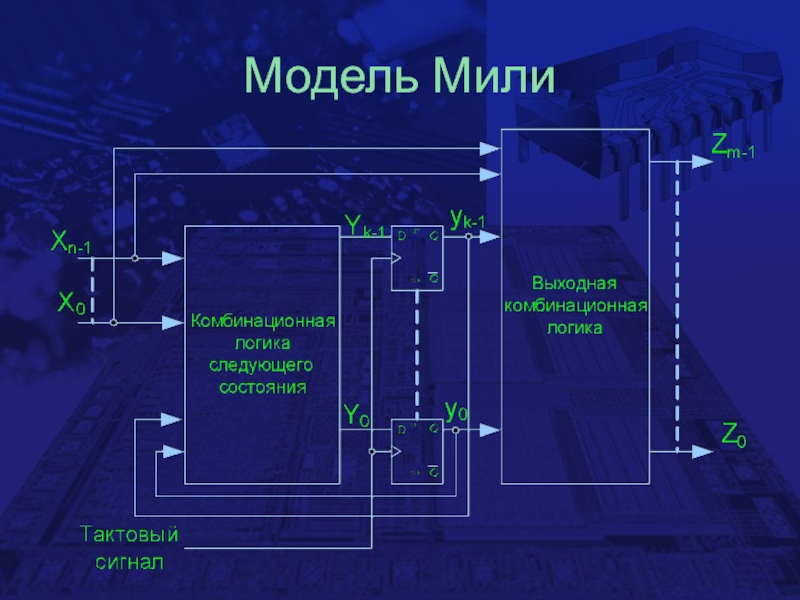
- 4. Модель Мили
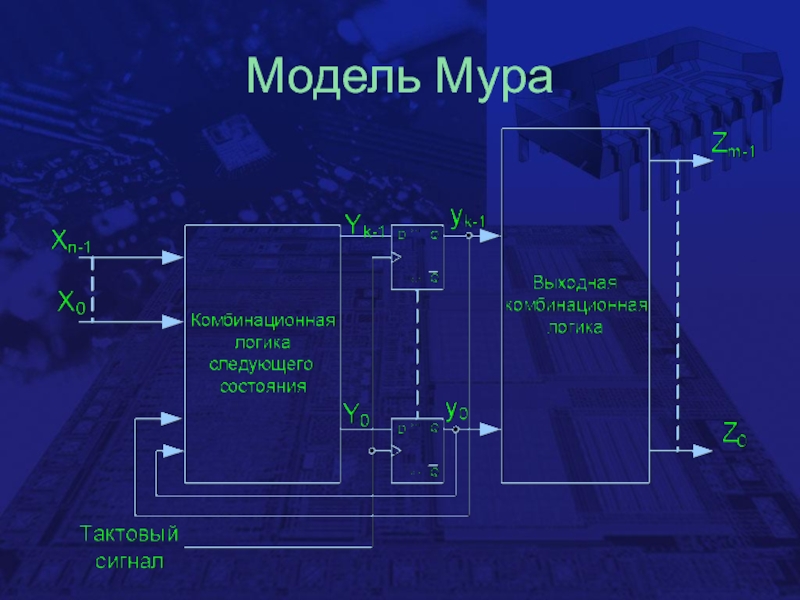
- 5. Модель Мура
- 6. Отличия моделей Мура и МилиВ модели Мили
- 7. Построение последовательной схемы на основе моделиНеобходимо получить
- 8. Счетчик с двумя произвольными счетными последовательностямиДопустим необходимо
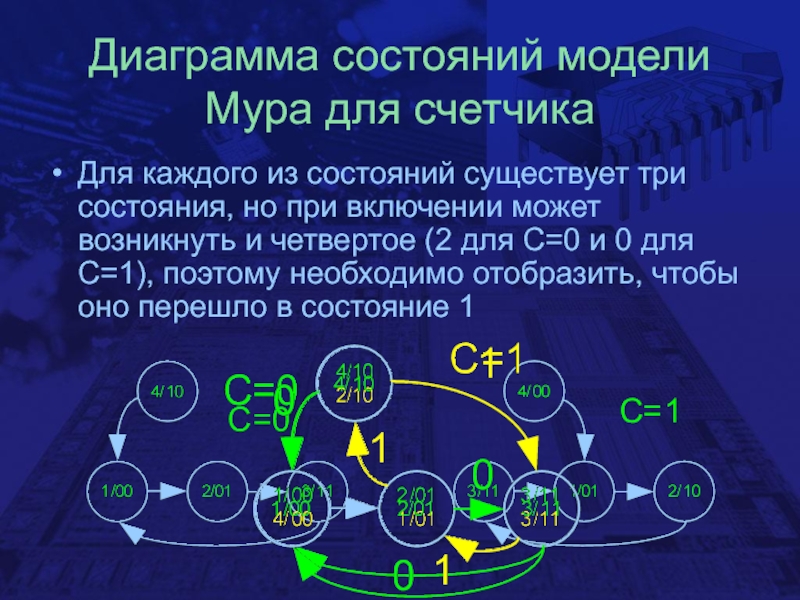
- 9. Диаграмма состояний модели Мура для счетчикаДля каждого
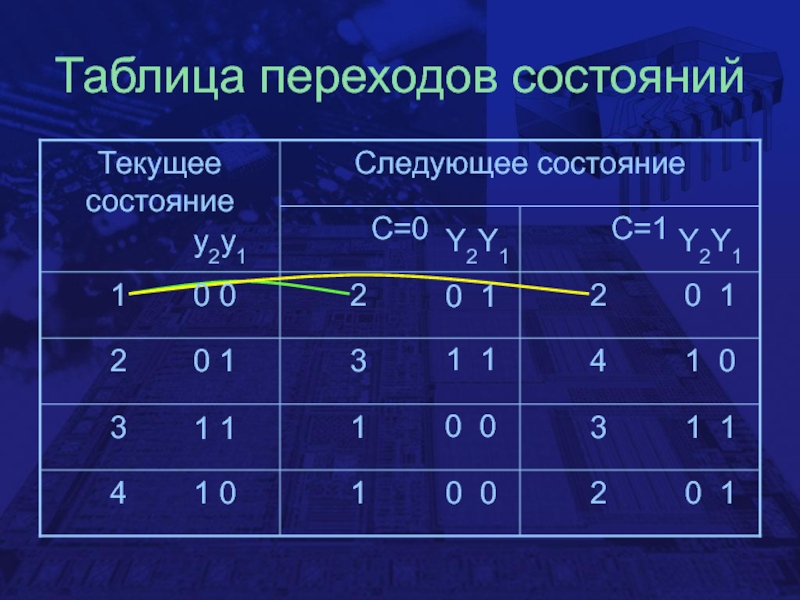
- 10. Таблица переходов состояний0 00 11 11 00 11 10 00 00 11 01 10 1y2y1Y2Y1Y2Y1
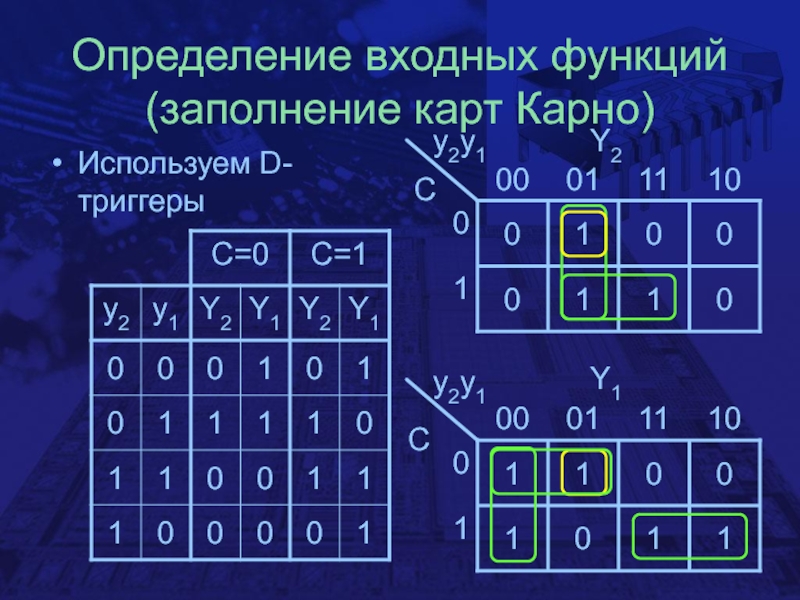
- 11. Определение входных функций (заполнение карт Карно) Используем D-триггерыy2y1y2y1ССY2Y1
- 12. Определение входных функций (построение схемы)Y2=y2y1+y1C=y2y1C+y1CY1=y2C+y2C+y2y1=y2y1+y2y1C+y2C
- 13. Детекторы последовательностиПусть необходимо построить схему, которая детектировала
- 14. Алгоритм проектированияПостроение диаграммы состоянийПостроение таблицы переходов состоянийПрисвоение
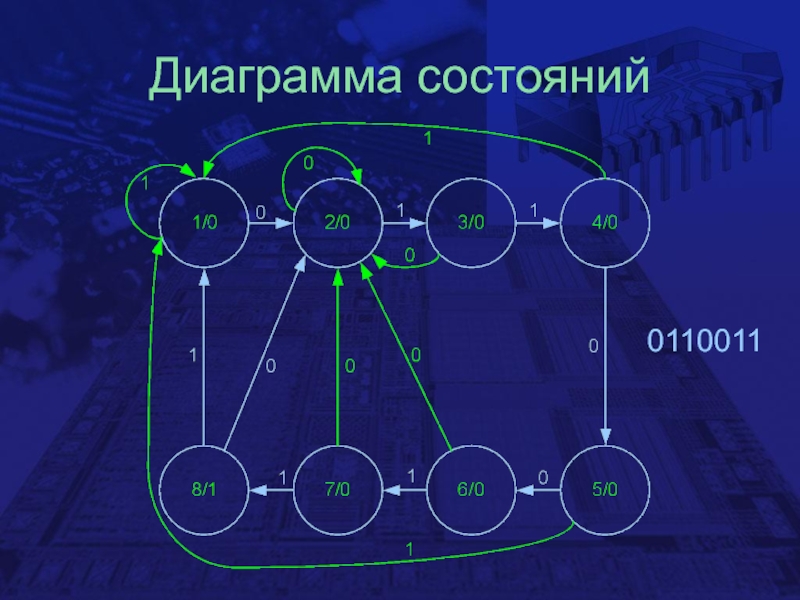
- 15. Диаграмма состояний0110011
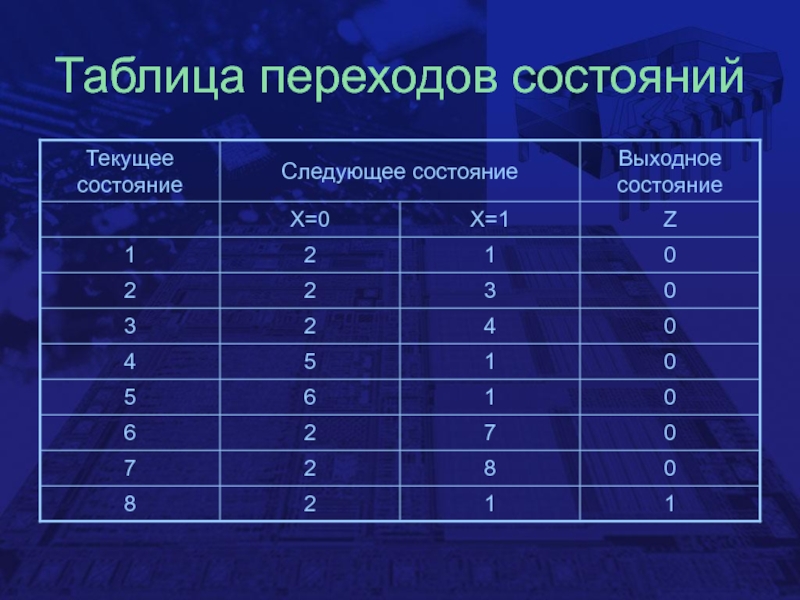
- 16. Таблица переходов состояний
- 17. Назначение состояниям значений переменныхДля описания 8 различных
- 18. Правило 1При переходе в одинаковое следующее состояние,
- 19. Правило 2Следующим состоянием, в которое могут переходить текущее состояние, следует назначать коды, отличающиеся только одной переменной
- 20. Правило 3Состояниям с одинаковым значением на выходе
- 21. Код ГреяКод, характеризуемый тем, что все его
- 22. Назначение состоянийСостояние 1 → 000Состояние 4 →
- 23. Таблица назначенных состояний
- 24. Входные функции триггеровy2y1xy3y2y1xy3y2y1xy3Y3=xy1+xy3+y2y1Y2=x+y3y2y1Y1=y3y1+y3y2y1+xy2y1++xy2y1
- 25. Выходная функцияПолучается непосредственно из столбца текущих значений в таблице назначенийZ=y3y2y1y2y1y3Z
- 26. Проектирование на основе модели МилиИспользуется тот же
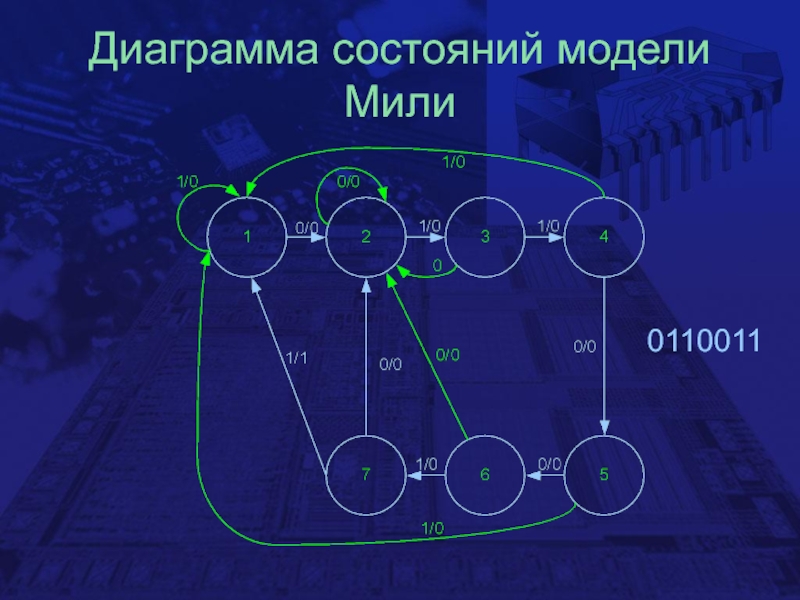
- 27. Диаграмма состояний модели Мили0110011
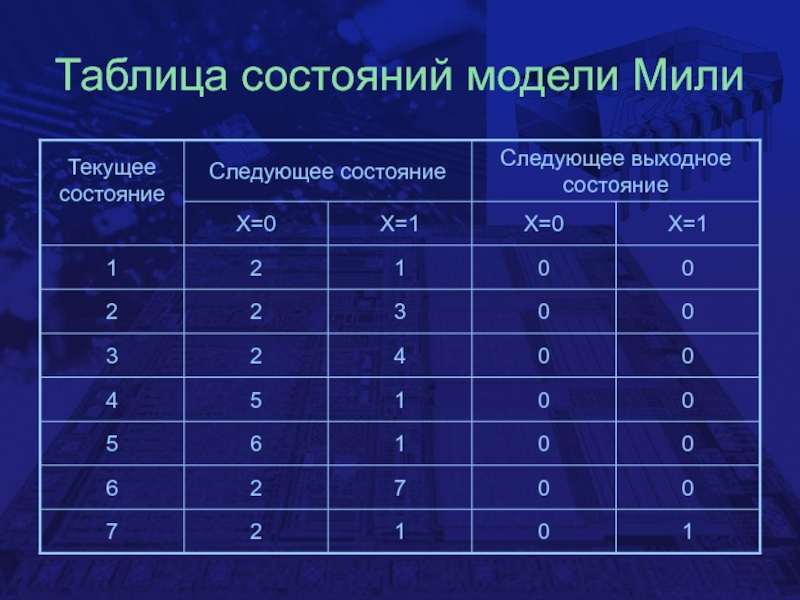
- 28. Таблица состояний модели Мили
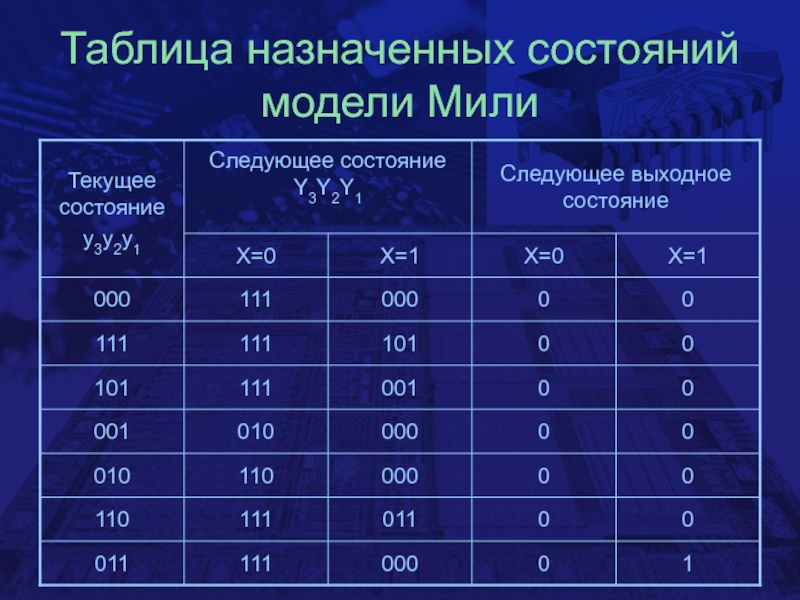
- 29. Таблица назначенных состояний модели Мили
- 30. Входные и выходная функции триггеровY3=xy1+xy3+y3y2y1+xy2y1Y2=x+y3y1Y1=y3+xy2y1+xy2y1Z=xy3y2y1
- 31. Минимизация количества состоянийИдентичные состояния – это состояния,
- 32. Эквивалентные состоянияДва состояния называются эквивалентными, и, следовательно,
- 33. Скачать презентанцию
Конечные автоматыВ реальных последовательных схемах существует конечное число логических состояний, поэтому их общее название – конечные автоматы.Состояние схемы можно представить двоичными сигналами, называемыми – переменными состояниями, где каждое состояние характеризуется однозначной
Слайды и текст этой презентации
Слайд 2Конечные автоматы
В реальных последовательных схемах существует конечное число логических состояний,
поэтому их общее название – конечные автоматы.
двоичными сигналами, называемыми – переменными состояниями, где каждое состояние характеризуется однозначной для него комбинацией значений переменных, хранящихся в триггерах и активизирующихся по внешнему тактовому сигналу.Слайд 3Модели синхронных последовательных схем
Существуют две различные модели:
Модель Мили (Mealy model)
Модель
Мура (Moore model)
Условные обозначения:
Хn-1,..,X0 – n входов схемы;
Zm-1,..,Z0 – m
выходов схемы;yk-1,..,y0 – k переменных текущих состояний (их значения хранятся в триггерах)
Yk-1,..,Y0 – k переменных следующих состояний (формируются для изменения состояния схемы)
Слайд 6Отличия моделей Мура и Мили
В модели Мили выходные сигналы схемы
представляют собой комбинационные функции, включающие входные сигналы, что может привести
к изменению сигнала на выходе без синхронизации с приходом тактового импульсаМодель Мура позволяет избежать этого, устанавливая зависимость выходных переменных от переменных текущих состояний
Слайд 7Построение последовательной схемы на основе модели
Необходимо получить комбинационную функцию переменных
следующих состояний (Y) и выходные сигналы (Z)
Для этого в первую
очередь необходимо определить количество триггеров (k). При количестве состояний схемы от 2k-1+1 до 2k необходимо иметь k триггеров.Слайд 8Счетчик с двумя произвольными счетными последовательностями
Допустим необходимо создать счетчик, счетная
последовательность которого при С=0: 0→1 →3, а при С=1: 1→2→3
Выберем
модель Мура, поскольку выходы схемы являются выходами триггеровНеобходимо составить диаграмму состояний модели мура для указанного счетчика
Далее составляется таблица переходов состояний
Слайд 9Диаграмма состояний модели Мура для счетчика
Для каждого из состояний существует
три состояния, но при включении может возникнуть и четвертое (2
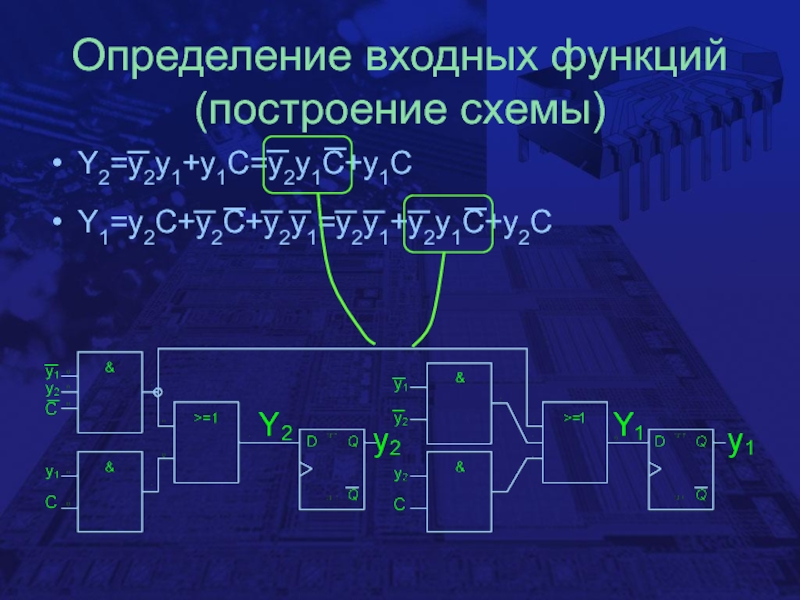
для C=0 и 0 для С=1), поэтому необходимо отобразить, чтобы оно перешло в состояние 1Слайд 12Определение входных функций (построение схемы)
Y2=y2y1+y1C=y2y1C+y1C
Y1=y2C+y2C+y2y1=y2y1+y2y1C+y2C
Слайд 13Детекторы последовательности
Пусть необходимо построить схему, которая детектировала определенную кодовую последовательность,
поступающую через единственный вход данных, и выдавала бы результат на
единственный выходПредположим нужно определить наличие на входе последовательности: 0110011
Слайд 14Алгоритм проектирования
Построение диаграммы состояний
Построение таблицы переходов состояний
Присвоение состояниям схемы комбинаций
значений переменных состояний
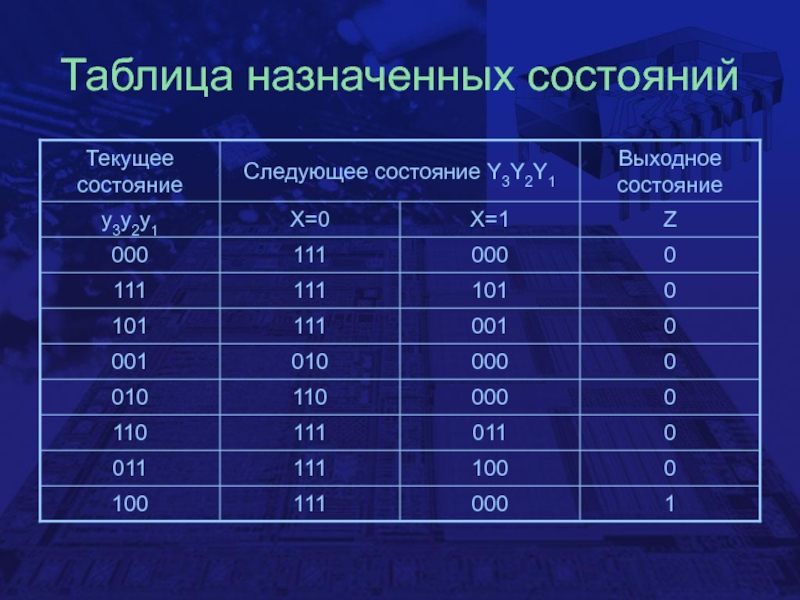
Построение таблицы назначенных состояний
Получение входных функций триггеров (с
помощью карт Карно)Получение по картам Карно выходных функций
Построение логической схемы
Слайд 17Назначение состояниям значений переменных
Для описания 8 различных состояний требуется 3
переменных состояния
Назначение значений может быть произвольным
Назначение значений следует проводить таким
образом, чтобы получить наиболее простую форму выходных функцийДля этого существуют 3 правила
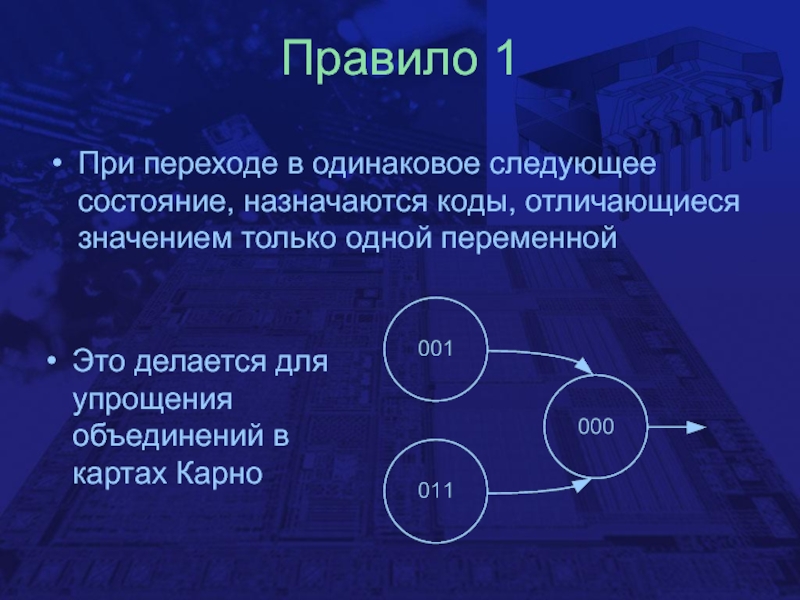
Слайд 18Правило 1
При переходе в одинаковое следующее состояние, назначаются коды, отличающиеся
значением только одной переменной
Это делается для упрощения объединений в картах
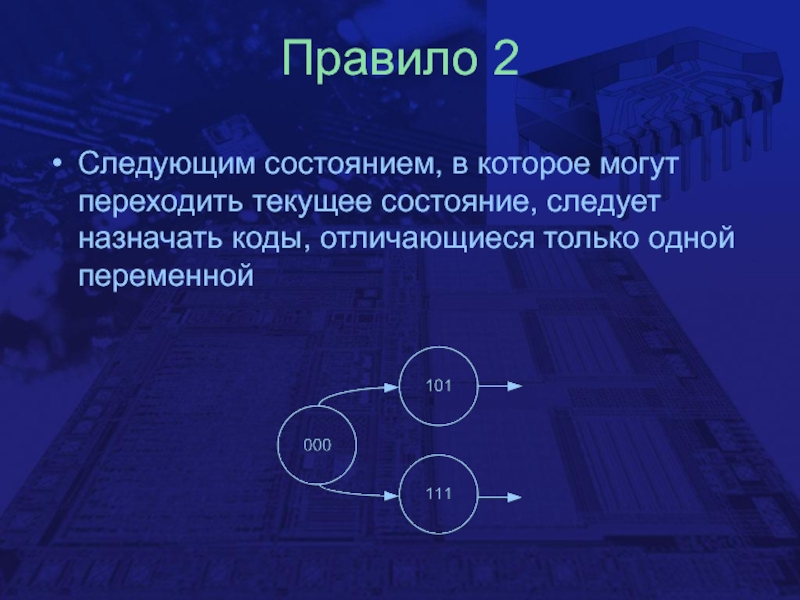
Карно Слайд 19Правило 2
Следующим состоянием, в которое могут переходить текущее состояние, следует
назначать коды, отличающиеся только одной переменной
Слайд 20Правило 3
Состояниям с одинаковым значением на выходе (с одинаковыми входными
значениями) следует назначать коды, отличающиеся значением одной переменной
Слайд 21Код Грея
Код, характеризуемый тем, что все его соседние комбинации отличаются
значением только одного бита называется кодом Грея
Все указанные три правила
являются лишь рекомендацией, позволяющей упростить выходные функции, однако это не значит, что они будут использовать минимальное количество вентилейСлайд 22Назначение состояний
Состояние 1 → 000
Состояние 4 → 001
Состояние 5 →
010
Состояние 8 → 100
Состояние 2 → 111
Состояние 3 → 101
Состояние
6 → 110Состояние 7 → 011
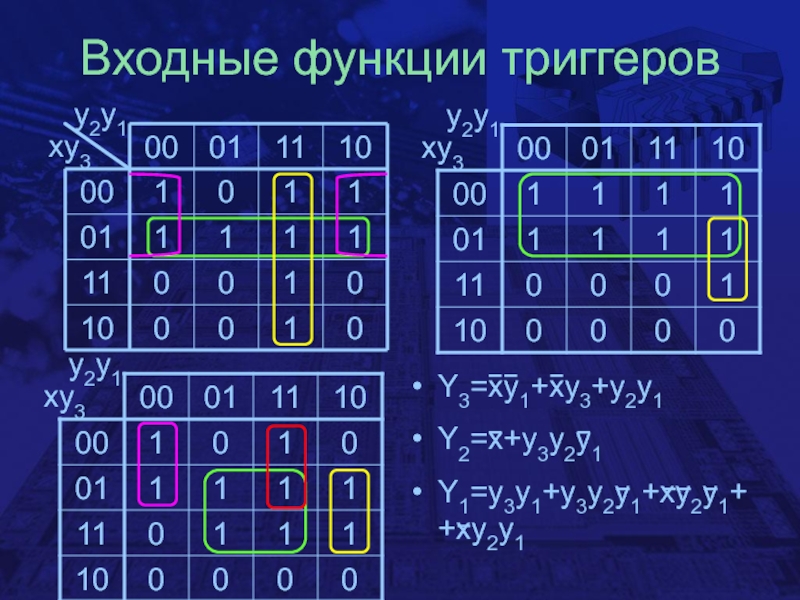
Слайд 24Входные функции триггеров
y2y1
xy3
y2y1
xy3
y2y1
xy3
Y3=xy1+xy3+y2y1
Y2=x+y3y2y1
Y1=y3y1+y3y2y1+xy2y1++xy2y1
Слайд 25Выходная функция
Получается непосредственно из столбца текущих значений в таблице назначений
Z=y3y2y1
y2y1
y3
Z
Слайд 26Проектирование на основе модели Мили
Используется тот же алгоритм, что и
при проектировании на модели Мура
На диаграмме состояний модели Мили над
дугами, направленными к состоянию, указываются как входные, так и выходные сигналы, которые приводят к переходу в данное состояниеСлайд 30Входные и выходная функции триггеров
Y3=xy1+xy3+y3y2y1+xy2y1
Y2=x+y3y1
Y1=y3+xy2y1+xy2y1
Z=xy3y2y1
Слайд 31Минимизация количества состояний
Идентичные состояния – это состояния, с одними и
теми же выходными сигналами, которые могут быть объединены
Эквивалентные состояния –
это состояния, которые можно свести к одному, если в схеме уже имеются другие такие же состояния или уже были сделаны таковымиСлайд 32Эквивалентные состояния
Два состояния называются эквивалентными, и, следовательно, могут быть заменены
одним, если выполняются следующие условия:
Выходные сигналы (текущие для модели Мура
и следующие для модели Мили), связанные с этими двумя состояниями, одинаковые;Соответствующие следующие состояния также одинаковы или эквивалентны.