Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Планиметрия Окружность. Касательная к окружности. Вписанные и центральные углы
Содержание
- 1. Планиметрия Окружность. Касательная к окружности. Вписанные и центральные углы
- 2. Окружностьэлементы окружности;касательная к окружности;вписанные и центральные углы.
- 3. ОкружностьОкружность – это фигура, которая состоит из всех точек плоскости, равноудаленных от данной.окружность
- 4. ОкружностьОкружность – это фигура, которая состоит из
- 5. ОкружностьОкружность – это фигура, которая состоит из
- 6. Расположение окружности и прямой в зависимости от
- 7. Касательная к окружностиРадиус, проведенный к точке касания,
- 8. Что и требовалось доказать.Если две прямые перпендикулярны третьей прямой, то они параллельны.
- 9. Свойство касательныхОтрезки касательных к окружности, проведенные из
- 10. Слайд 10
- 11. Признак касательнойЕсли прямая проходит через конец радиуса,
- 12. Слайд 12
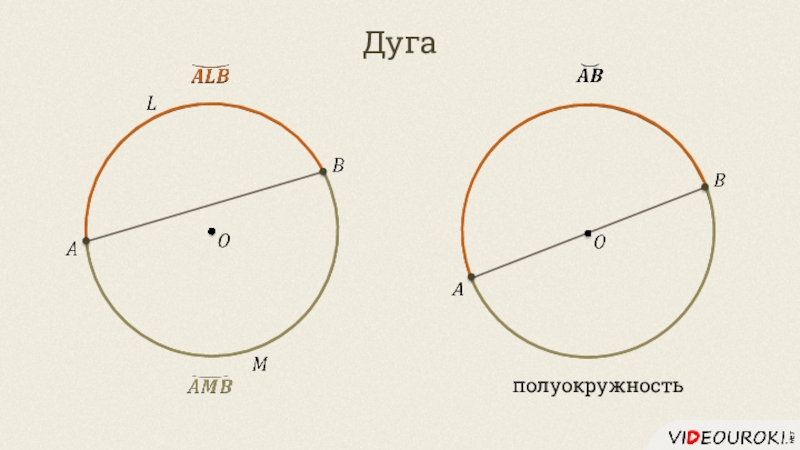
- 13. Дугаполуокружность
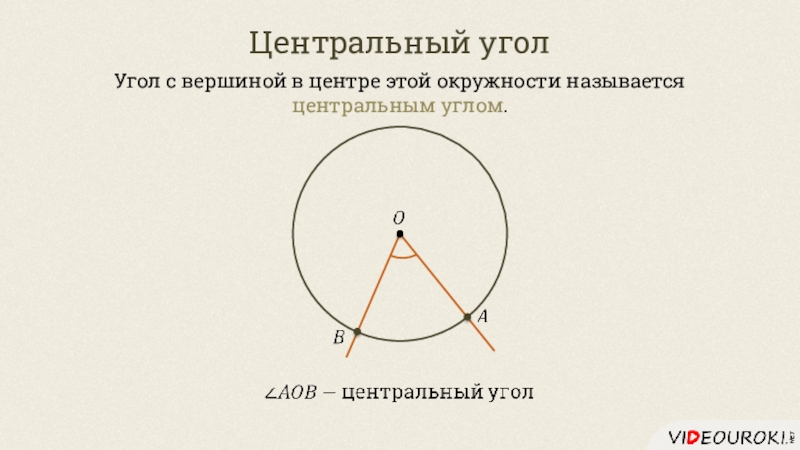
- 14. Центральный уголУгол с вершиной в центре этой окружности называется центральным углом.
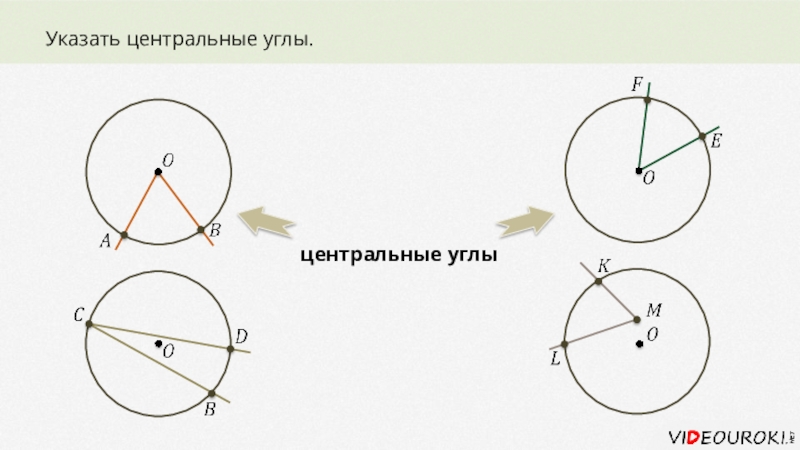
- 15. Указать центральные углы.центральные углы
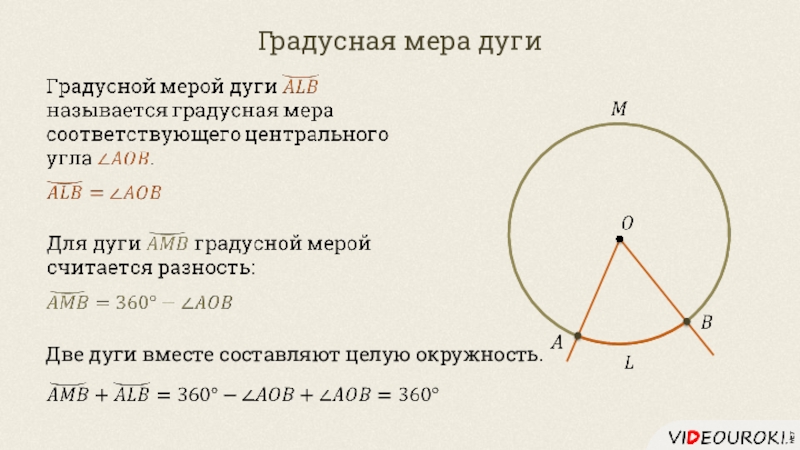
- 16. Градусная мера дугиДве дуги вместе составляют целую окружность.
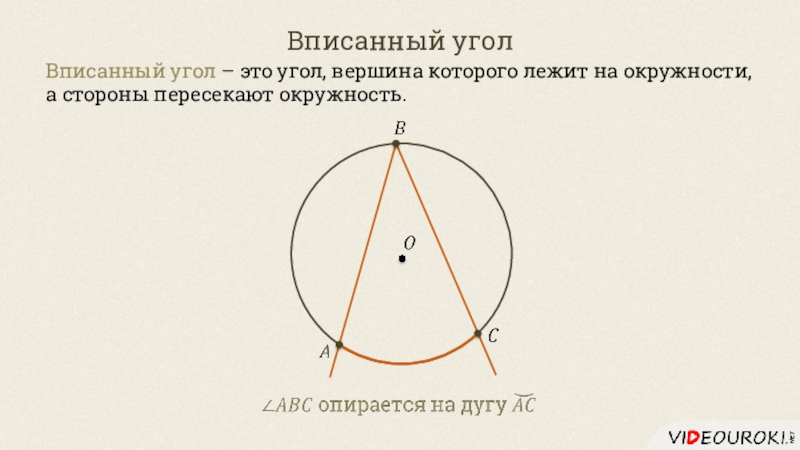
- 17. Вписанный уголВписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
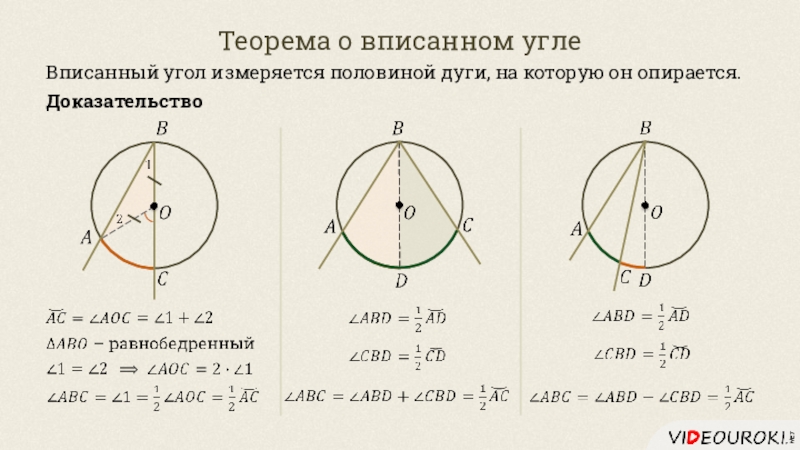
- 18. Теорема о вписанном углеВписанный угол измеряется половиной дуги, на которую он опирается.Доказательство
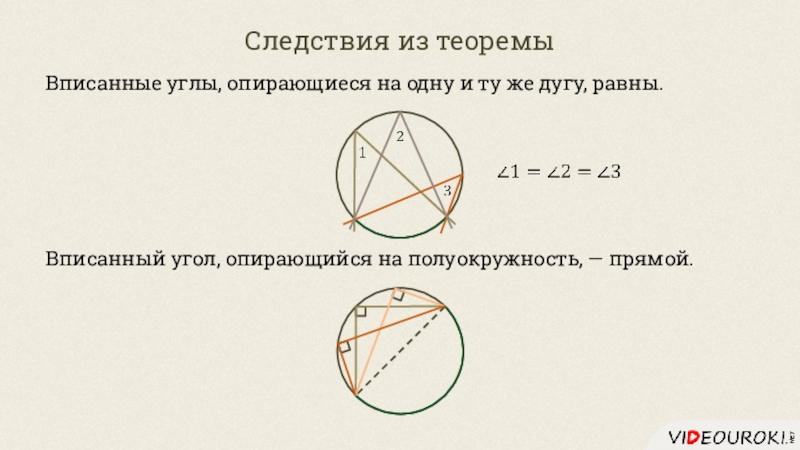
- 19. Следствия из теоремыВписанные углы, опирающиеся на одну
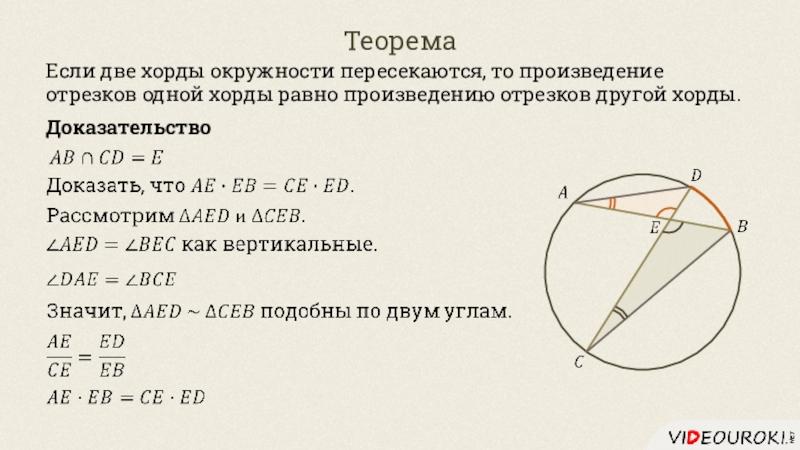
- 20. ТеоремаЕсли две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.Доказательство
- 21. Слайд 21
- 22. СледствияУгол между касательной и хордой, проведенной в
- 23. Окружность. Касательная к окружности. Вписанные и центральные углы
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Окружность
Окружность – это фигура, которая состоит из всех точек плоскости,
равноудаленных от данной.
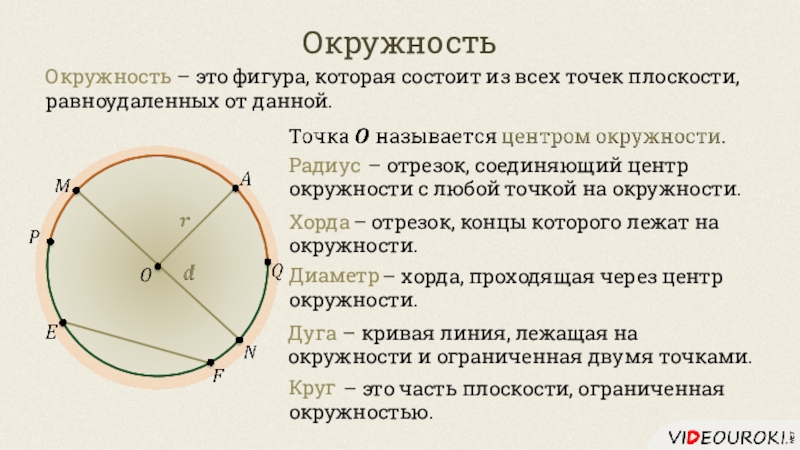
Слайд 4Окружность
Окружность – это фигура, которая состоит из всех точек плоскости,
равноудаленных от данной.
Радиус
Дуга
Хорда
Диаметр
Круг
– отрезок, соединяющий центр окружности с любой точкой на окружности. – отрезок, концы которого лежат на окружности.
– хорда, проходящая через центр окружности.
– кривая линия, лежащая на окружности и ограниченная двумя точками.
– это часть плоскости, ограниченная окружностью.
Слайд 5Окружность
Окружность – это фигура, которая состоит из всех точек плоскости,
равноудаленных от данной.
Радиус
Дуга
Хорда
Диаметр
Круг
– отрезок, соединяющий центр окружности с любой точкой на окружности. – отрезок, концы которого лежат на окружности.
– хорда, проходящая через центр окружности.
– кривая линия, лежащая на окружности и ограниченная двумя точками.
– это часть плоскости, ограниченная окружностью.
Сегмент
Сегмент
Сектор
Слайд 6Расположение окружности и прямой в зависимости от отношения расстояния от
центра окружности до прямой и радиуса окружности
Если расстояние от центра
окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
Слайд 7Касательная к окружности
Радиус, проведенный к точке касания, перпендикулярен касательной.
Доказательство
Свойство
касательной к окружности:
касательная к окружности перпендикулярна к радиусу, проведенному
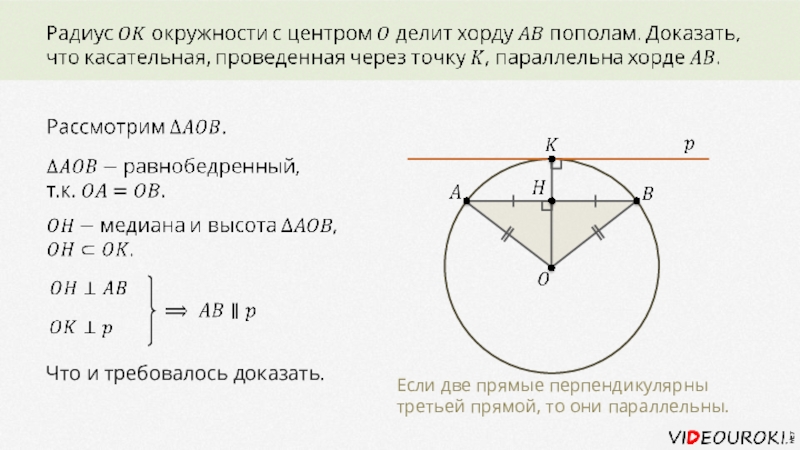
в точку касания.Слайд 8Что и требовалось доказать.
Если две прямые перпендикулярны третьей прямой, то
они параллельны.
Слайд 9Свойство касательных
Отрезки касательных к окружности, проведенные из одной точки, равны
и составляют равные углы с прямой, проходящей через эту точку
и центр окружности.Что и требовалось доказать.
Доказательство
Слайд 11Признак касательной
Если прямая проходит через конец радиуса, лежащий на окружности,
и перпендикулярна к этому радиусу, то она является касательной.
То есть
радиус окружности и расстояние до прямой равны.Доказательство
Данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой.
А значит, он является расстоянием от центра окружности до прямой.
Прямая является касательной к окружности.
Что и требовалось доказать.
Слайд 17Вписанный угол
Вписанный угол – это угол, вершина которого лежит на
окружности, а стороны пересекают окружность.
Слайд 18Теорема о вписанном угле
Вписанный угол измеряется половиной дуги, на которую
он опирается.
Доказательство
Слайд 19Следствия из теоремы
Вписанные углы, опирающиеся на одну и ту же
дугу, равны.
Вписанный угол, опирающийся на полуокружность, — прямой.
Слайд 20Теорема
Если две хорды окружности пересекаются, то произведение отрезков одной хорды
равно произведению отрезков другой хорды.
Доказательство
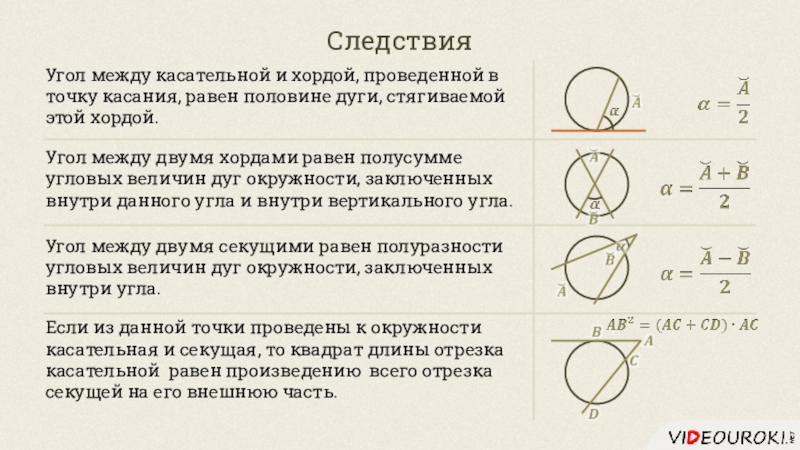
Слайд 22Следствия
Угол между касательной и хордой, проведенной в точку касания, равен
половине дуги, стягиваемой этой хордой.
Угол между двумя хордами равен полусумме
угловых величин дуг окружности, заключенных внутри данного угла и внутри вертикального угла.Угол между двумя секущими равен полуразности угловых величин дуг окружности, заключенных внутри угла.
Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть.