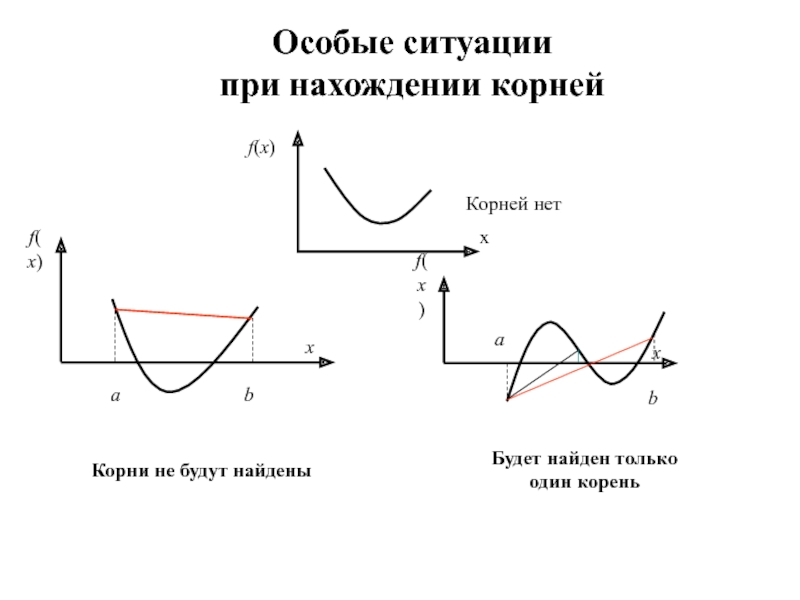
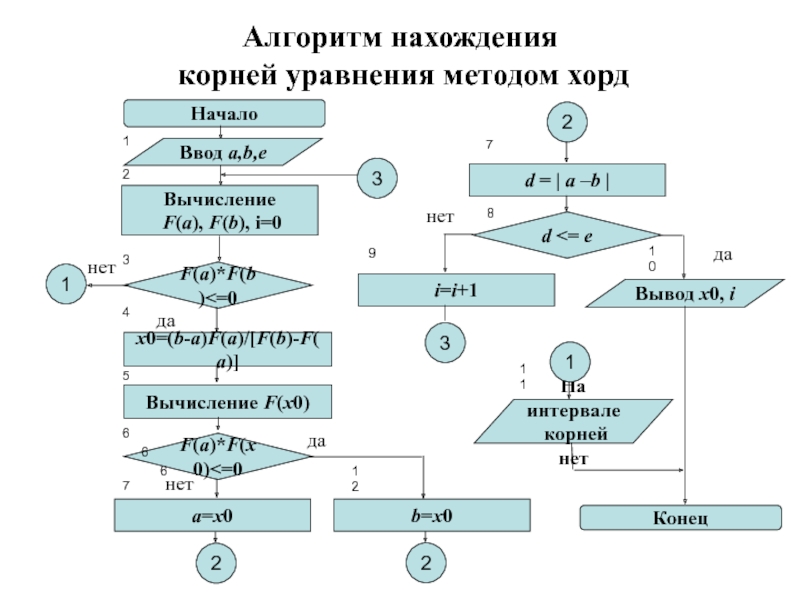
наличия корня на интервале [a, b]: если F(a)*F(b) < 0,
то интервал содержит корни уравнения, если F(a)*F(b) > 0, то интервал не содержит корней.Вычисление x0 = a – (b -a)*F(a)/[F(b) – F(a)].
Вычисление F(x0).
Проверка условия F(а)*F(х0) <=0: если «да», то b=x0, если «нет», то а=х0.
Вычисление погрешности d =|a - b|
Проверка достижения заданной точности:
если d <= е, то решение найдено х0 – корень уравнения;
если d > е, то продолжить деление отрезка, т.е. перейти к п. 2.
F(a)
F(x)
x
b
a
F(b)
F(x0)
x0
![Презентация на тему Нахождение корней уравнения методом хордЗадание интервала [a, b].Вычисление Нахождение корней уравнения методом хордЗадание интервала [a, b].Вычисление F(a) и F(b).Проверка наличия корня на интервале [a, b]:](/img/thumbs/16be778874ec018f57d3f3f6419d2fd7-800x.jpg)

![Нахождение корней уравнения методом хорд Нахождение корней уравнения методом дихотомииЗадание интервала [a, b].Вычисление F(a) и F(b).Проверка Нахождение корней уравнения методом дихотомииЗадание интервала [a, b].Вычисление F(a) и F(b).Проверка наличия корня на интервале [a, b]:](/img/thumbs/ed6e5ed7c2f2190a0646cfc3041d45ab-800x.jpg)