Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Научно-исследовательская работа «Загадка чисел Фибоначчи»
Содержание
- 1. Научно-исследовательская работа «Загадка чисел Фибоначчи»
- 2. ВопросИстинно ли наличие ряда чисел Фибоначчи в человеческом теле?
- 3. ГипотезаРяд чисел Фибоначчи играют главную роль не только в математике, но и в пропорциях человеческого тела.
- 4. Цель работы экспериментальным путем выяснить истинность наличия
- 5. Задачи проекта 1) Изучить теорию и историю
- 6. Теоретическая часть:Леонардо ФибоначчиЛеона́рдо Пиза́нский (лат. Leonardus Pisanus,
- 7. Происхождение чисел«Некто поместил пару кроликов в некоем
- 8. Свойства последовательности Фибоначчи0, 1, 1, 2, 3,
- 9. Золотое сечениеБолее того, после 13-ого числа в
- 10. Числа и спираль Фибоначчи
- 11. Слайд 11
- 12. Вид из космоса. Спираль Фибоначчи
- 13. Практическая часть Объект исследования: человекВозраст: 17 лет
- 14. Числа Фибоначчи в строении рук у человека
- 15. Измерение ладони. 1Нам понадобится измерить: третью,
- 16. №1 Шойлаа Чайзат 1) 2,2мм+2,9 мм =
- 17. №2 Монгуш Тензин-Шыырап 1)2,7мм+3,1мм=5,8 мм;2)3,1мм+5,8мм=8,9 мм:Получаем последовательность из чисел 27, 31, 58, 89.
- 18. №3Монгуш Чимис 1)2,0мм+2,5мм=4,5мм2)2,5мм+4,5мм=7,0ммПолучаем последовательность из чисел 20, 25, 45, 70.
- 19. Ооржак Кежик 17 лет
- 20. Вычисления
- 21. ВыводВидим, что пропорция "фи", которая равна отношению
- 22. Список литературы и сайтов Интернета: 1. Воробьев
- 23. Спасибо за внимание
- 24. Скачать презентанцию
ВопросИстинно ли наличие ряда чисел Фибоначчи в человеческом теле?
Слайды и текст этой презентации
Слайд 1Выполнил: ученик 11 кл
Монгуш тензин-Шыырап
Научный руководитель:
учитель химии и
биологии Ооржак А.А.
«Загадка чисел Фибоначчи»Слайд 3Гипотеза
Ряд чисел Фибоначчи играют главную роль не только в математике,
но и в пропорциях человеческого тела.
Слайд 4Цель работы
экспериментальным путем выяснить истинность наличия последовательности чисел Фибоначчи
в результате измерения строения некоторых частей тела
Слайд 5Задачи проекта
1) Изучить теорию и историю ряда чисел Фибоначчи
2) Измерить
некоторые части человека и записать результаты в таблицу.
3) Провести математические
вычисления.4) Сделать вывод.
Слайд 6Теоретическая часть:
Леонардо Фибоначчи
Леона́рдо Пиза́нский (лат. Leonardus Pisanus, итал. Leonardo Pisano,
около 1170 года, Пиза — около 1250 года, там же)
— первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи. Он открывает ряд чисел.Слайд 7Происхождение чисел
«Некто поместил пару кроликов в некоем месте, огороженном со
всех сторон стеной, чтобы узнать, сколько пар кроликов родится при
этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения».Поскольку первая пара кроликов — новорожденные, то на второй месяц они не дадут приплода, и останется одна пара. На третий месяц они произведут одну пару: 1 + 1 = 2. На четвертый месяц из двух пар потомство даст лишь одна пара (вторая еще не дает приплода): 2 + 1 = 3 пары. На пятый месяц две родившиеся на третий месяц пары дадут потомство: 3 + 2 = 5 пар. На шестой месяц потомство дадут только те пары, которые родились на четвертом месяце: 5 + 3 = 8 пар и т. д.
Слайд 8Свойства последовательности Фибоначчи
0, 1, 1, 2, 3, 5, 8, 13,
21, 34, 55, 89, 144, 233, 377, 610, 987, 1597,
2584, ... Это и есть ряд Фибоначчикаждое число в этой последовательности получается из суммы двух предыдущих чисел.
В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то пpевосходящая, то не достигающая его. (Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично)
Слайд 9Золотое сечение
Более того, после 13-ого числа в последовательности этот результат
деления становится постоянным до бесконечности ряда… Именно это постоянное число
деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)Итак, Золотая пропорция = 1 : 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
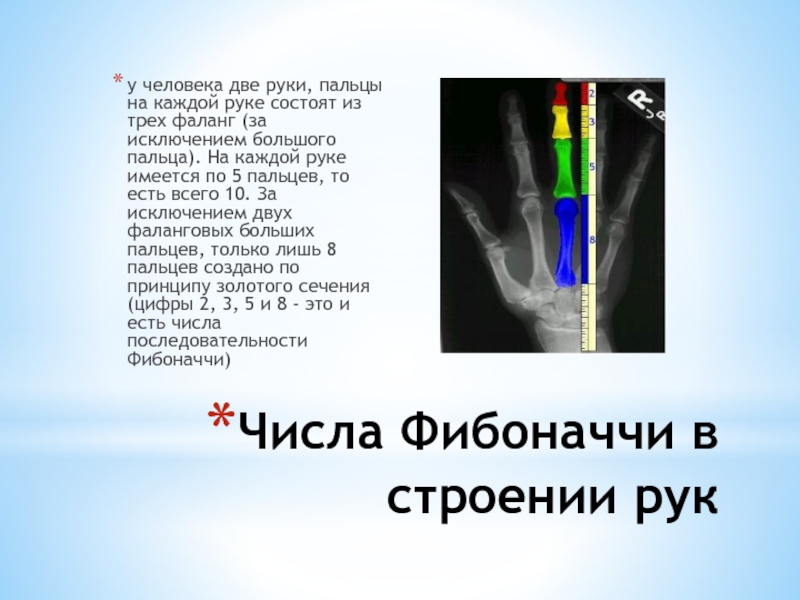
Слайд 14Числа Фибоначчи в строении рук
у человека две руки, пальцы
на каждой руке состоят из трех фаланг (за исключением большого
пальца). На каждой руке имеется по 5 пальцев, то есть всего 10. За исключением двух фаланговых больших пальцев, только лишь 8 пальцев создано по принципу золотого сечения (цифры 2, 3, 5 и 8 - это и есть числа последовательности Фибоначчи)Слайд 15 Измерение ладони.
1Нам понадобится измерить: третью, вторую, первую фалангу пальцев,
третью кость кисти трех человека.
2. Оборудование: школьная линейка, фломастер.
3. Предмет
обследования: кисть руки.4. Измерение.
Для начала приготовим ладони для измерения и последовательно выполняем действия:
4.1) На руках отметим границы сгиба пальцев рук
4.2) Измерим 3-ю фалангу пальцев
4.3) Аналогично диагностируем 2-ю и 1-ю фалангу пальцев
4.4) Фиксируем вдоль третьей кости кисти
4.5) Заполняем таблицу после проведения всех трех действий
Слайд 16№1 Шойлаа Чайзат
1) 2,2мм+2,9 мм = 5,1мм;
2) 2,9мм+5,1 мм =
8,0 мм.
Получаем последовательность из чисел 22, 29, 51, 80.
Слайд 17№2 Монгуш Тензин-Шыырап
1)2,7мм+3,1мм=5,8 мм;
2)3,1мм+5,8мм=8,9 мм:
Получаем последовательность из чисел 27, 31,
58, 89.
Слайд 18№3Монгуш Чимис
1)2,0мм+2,5мм=4,5мм
2)2,5мм+4,5мм=7,0мм
Получаем последовательность из чисел 20, 25, 45, 70.
Слайд 21Вывод
Видим, что пропорция "фи", которая равна отношению соседних чисел из
ряда Фибоначчи , проявляется и в человеческом теле.
После проведения эксперимента
я выяснила, что числовая последовательность Фибоначчи встречается не только в математической практике, но и в анатомии, которая будет играть важную роль в медицине. Таким образом, наша гипотеза о существовании особых числовых закономерностей, которые отвечают за гармонию, подтверждается.
Действительно, всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой!
Слайд 22Список литературы и сайтов Интернета:
1. Воробьев Н. Н. Числа Фибоначчи.
– М., Наука, 1984.
2. Гика М. Эстетика пропорций в природе
и искусстве. – М., 1936. 3. Дмитриев А. Хаос, фракталы и информация. // Наука и жизнь, № 5, 2001.
4. Кашницкий С. Е. Гармония, сотканная из парадоксов // Культура и
жизнь. – 1982.– № 10.
5. Малай Г. Гармония – тождество парадоксов // МН. – 1982.– № 19.
6. Соколов А. Тайны золотого сечения // Техника молодежи. – 1978.– № 5.
7. Стахов А. П. Коды золотой пропорции. – М., 1984.
8. Урманцев Ю. А. Симметрия природы и природа симметрии. – М., 1974.
9. Урманцев Ю. А. Золотое сечение // Природа. – 1968.– № 11.
10. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три
взгляда на природу гармонии.-М., 1990.
11.Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. -М.:
Наука, 1972.
Теги