Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нейронные сети
Содержание
- 1. Нейронные сети
- 2. Базовые принципы технологии искусственных нейронных сетейМатематическое моделирование
- 3. Биологический нейронБиологический нейрон – базовая структурно-функциональная единица
- 4. Биологическая нейронная сетьГоловной мозг содержит ~30 миллиардов
- 5. Вычислительные возможностиСильноразветвленная сеть как мощная распараллеленная система
- 6. Развитие теории нейросетейИзучение строения мозга и мозговой
- 7. 1957 г. Фрэнк Розенблатт (Frank Rosenblatt)Основы искусственного
- 8. 1982 г. Теуво Кохонен (Teuvo Kohonen)Теория ассоциативной
- 9. 1990 г. Джефри Элман (Jeffrey Elman)Рекуррентные нейронные
- 10. Простая модель синаптической связиИскусственная нейронная сеть (ИНС)
- 11. ПерсептронАссоциативный A-элемент активизируется, как только количество сигналов
- 12. Математическая модель нейронаМатематически нейрон представляет собой взвешенный
- 13. Передаточные функции искусственных нейронов. Другие примеры:ЭкспонентаТригонометрический синусМодульнаяКвадратичнаяРадиально-базиснаяГиперболический
- 14. Принципы функционирования ИНСДействующие параллельно и соединенные последовательно
- 15. Преимущества нейросетевого подходаРешение задач, не поддающихся адекватной
- 16. Основные направления использования. 1) Восстановление образов, прогнозирование
- 17. Проблема синтеза ИНСЗадача синтеза требуемой искусственной сети
- 18. Алгоритмы обучения нейросетейПроцесс (алгоритм) обучения нейронной сети
- 19. Свойства успешно обученных ИНСОбучаемость/дообучаемость. Выбрав одну из
- 20. Обучение «С учителем»Путем анализа имеющихся входных/выходных данных,
- 21. Пример №1 – Решение не найдено(градиентный метод
- 22. Пример №2 – Достигнут локальный минимумПуть градиентного
- 23. Пример №3 – Достигнут глобальный минимумПуть градиентного
- 24. Алгоритм обратного распространения ошибки(Error Backpropagation)Пример реализации:t=1+sin(p*π/4)До начала
- 25. Обучение «Без учителя»Система обучается установлению принадлежности образа
- 26. Пример самообучения карты КохоненаКлассификация объектовдвух сортов на 2 классаКлассификация объектовдвух сортов на 4 класса
- 27. Области применения ИНСПрогнозирование и восстановление числовых рядовКластерный
- 28. Решение задач прогнозирования ивосстановления рядов данныхДолгосрочное прогнозирование
- 29. Решение задач прогнозирования ивосстановления рядов данныхОбъективная оценка
- 30. Решение задач прогнозирования ивосстановления рядов данныхПрогнозирование индексов
- 31. Решение задач прогнозирования ивосстановления рядов данныхИспользование ИНС
- 32. Решение задач прогнозирования ивосстановления рядов данныхПрогнозирование ионосферных
- 33. Решение задач прогнозирования ивосстановления рядов данныхРезультат прогноза
- 34. Решение задач классификации образовМногопараметрическая классификация последствий солнечной
- 35. Решение задач классификации образовЭффективность обучения нейронной сети
- 36. Решение задач классификации образовВ результате проведенной нейросетевой
- 37. Другие решенные задачи с применением ИНСВосстановление пробелов
- 38. Подробнее о технологии ИНС в геофизикеИстория развития
- 39. Интернет-сервисы на основе технологии ИНС в режиме
- 40. Слайд 40
- 41. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Технология искусственных нейронных сетей.
Применение нейросетей для решения геофизических задач
Ревунов Сергей
Евгеньевич
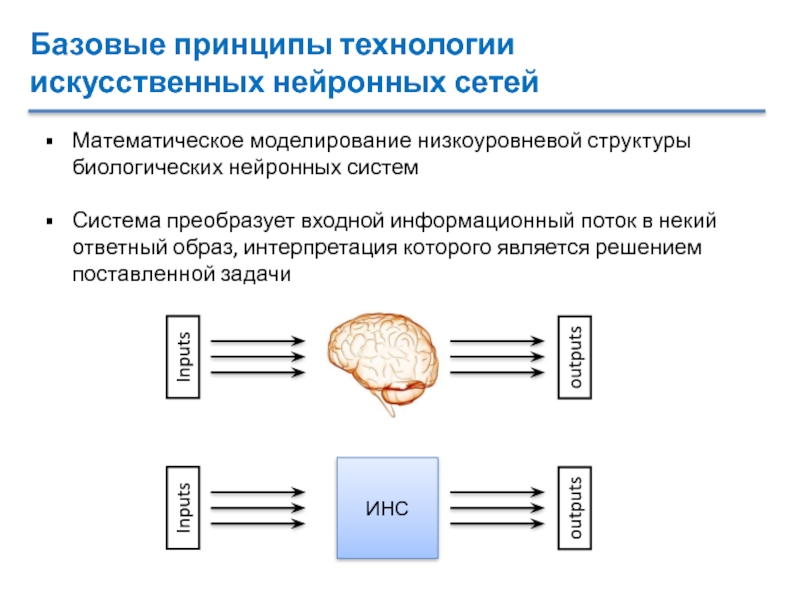
Слайд 2Базовые принципы технологии искусственных нейронных сетей
Математическое моделирование низкоуровневой структуры биологических
нейронных систем
Система преобразует входной информационный поток в некий ответный образ,
интерпретация которого является решением поставленной задачиСлайд 3Биологический нейрон
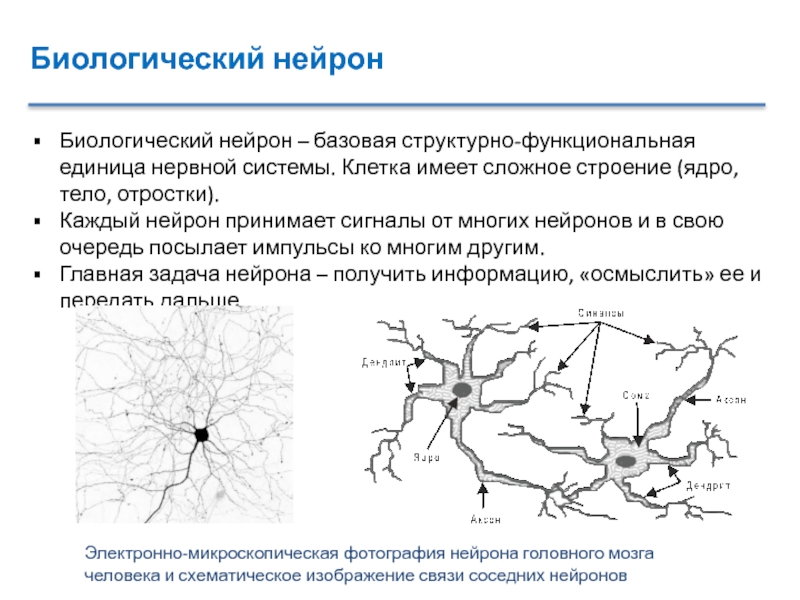
Биологический нейрон – базовая структурно-функциональная единица нервной системы. Клетка
имеет сложное строение (ядро, тело, отростки).
Каждый нейрон принимает сигналы от
многих нейронов и в свою очередь посылает импульсы ко многим другим.Главная задача нейрона – получить информацию, «осмыслить» ее и передать дальше.
Электронно-микроскопическая фотография нейрона головного мозга человека и схематическое изображение связи соседних нейронов
Слайд 4Биологическая нейронная сеть
Головной мозг содержит ~30 миллиардов нейронов в коре.
В слое площадью один квадратный миллиметр содержится ~50 тысяч нейронов.
В
среднем, на каждый нейрон приходится ~10 см нервных волокон. При этом каждый нейрон может иметь до 40 тысяч соединений.Электронно-микроскопическая фотография фрагмента биологической нейронной сети мозга взрослого человека
Слайд 5Вычислительные возможности
Сильноразветвленная сеть как мощная распараллеленная система реализует вычислительные возможности,
превосходящие производительность самых быстрых современных компьютеров.
Пример: распознавание образов через зрение
(отождествление знакомого лица в незнакомом окружении). Взаимодействие и обмен информацией между рецепторами и нейронами головного мозга.Мозг на протяжении всей жизни находится в динамическом состоянии. Он строит и разрушает миллионы связей между своими нейронами по собственным правилам на основании предшествующего опыта, непрерывно корректируя индивидуальные особенности личности.
Слайд 6Развитие теории нейросетей
Изучение строения мозга и мозговой активности в начале
ХХ века - фундамент вычислительных экспериментов с привлечением математического аппарата
Цель
- воспроизвести способность нервных биологических систем обучаться и исправлять ошибкиПопытки смоделировать лишь низкоуровневую нейронную структуру, т.к. было понятно, что мозг человека представляет собой исключительно сложную, нелинейную систему обработки информации
1943 г. американский математик и философ Норберт Винер (Norbert Wiener) - идея о представлении сложных биологических процессов простыми математическими моделями
1943 г. американский нейропсихолог Уоррен МакКаллок (Warren Sturgis McCulloch) и Уолтер Питтс (Walter Pitts) предложили первую модель нейрона и сформулировали основные положения теории функционирования головного мозга.
1949 г. канадский физиолог и нейропсихолог Дональд Хэбб (Donald Olding Hebb) - первый алгоритм обучения искусственных нейронных сетей
Слайд 71957 г. Фрэнк Розенблатт (Frank Rosenblatt)
Основы искусственного интеллекта
Первый нейрокомпьютер «Марк-1»
(1960 г.), способный обучаться и решать простейшие задачи. Особенность –
алгоритм перцептрона (персептрона).Персептрон – математическая модель восприятия информации мозгом, кибернетическая модель мозга.
Персептроны позволяют создать набор ассоциаций между входными стимулами и необходимой реакцией на выходе. В биологическом плане это соответствует преобразованию, например, зрительной информации в физиологический ответ от двигательных нейронов.
Слайд 81982 г. Теуво Кохонен (Teuvo Kohonen)
Теория ассоциативной памяти
Модели самообучающихся нейросетей
(нейронная сеть/слой Кохонена)
Решение нестандартных задач кластеризации и визуализации данных (самоорганизующаяся
карта Кохонена)Оригинальные алгоритмы обработки символьной информации
Слайд 91990 г. Джефри Элман (Jeffrey Elman)
Рекуррентные нейронные сети
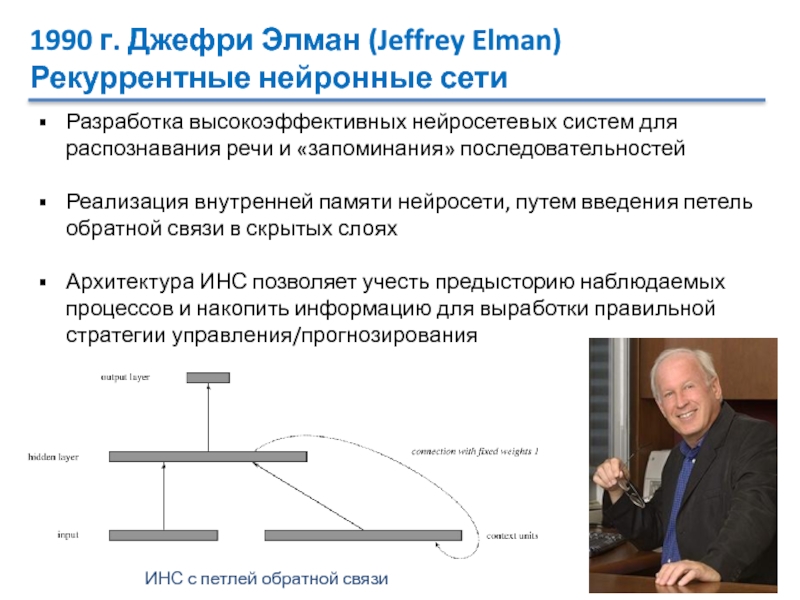
Разработка высокоэффективных нейросетевых
систем для распознавания речи и «запоминания» последовательностей
Реализация внутренней памяти нейросети,
путем введения петель обратной связи в скрытых слояхАрхитектура ИНС позволяет учесть предысторию наблюдаемых процессов и накопить информацию для выработки правильной стратегии управления/прогнозирования
Слайд 10Простая модель синаптической связи
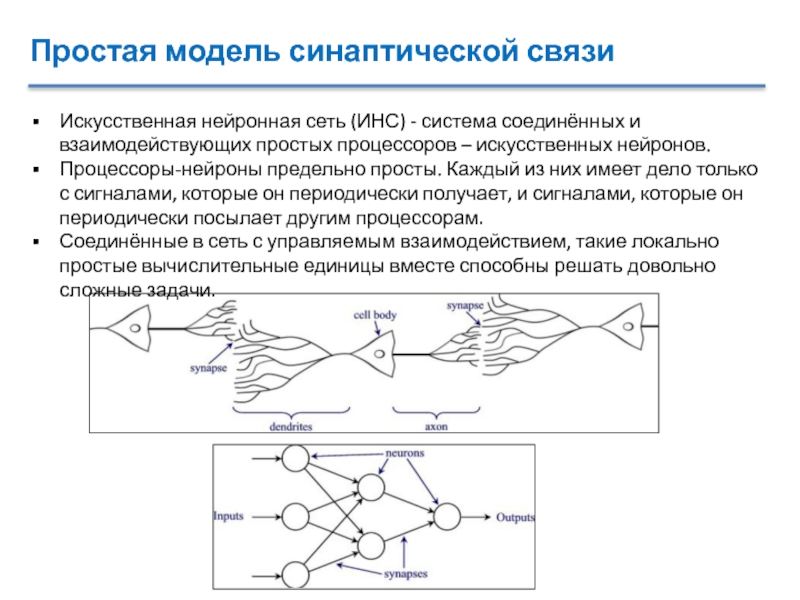
Искусственная нейронная сеть (ИНС) - система соединённых
и взаимодействующих простых процессоров – искусственных нейронов.
Процессоры-нейроны предельно просты. Каждый
из них имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам.Соединённые в сеть с управляемым взаимодействием, такие локально простые вычислительные единицы вместе способны решать довольно сложные задачи.
Слайд 11Персептрон
Ассоциативный A-элемент активизируется, как только количество сигналов от S-элементов на
его входе превысило некоторую пороговую величину θ.
Сигналы от «возбудившихся» A-элементов,
в свою очередь, передаются в сумматор R, причём сигнал от i-го ассоциативного элемента передаётся с коэффициентом wi (вес A-R связи). R-элемент подсчитывает сумму значений входных сигналов, помноженных на веса. R-элемент (персептрон), выдаёт «1», если превышен порог θ, иначе на выходе будет «−1».
Процесс обучения состоит в изменении весовых коэффициентов wi связей A-R.
На современном этапе однослойный персептрон представляет скорее исторический интерес, однако на его примере могут быть изучены основные понятия и простые алгоритмы обучения нейронных сетей.
Слайд 12Математическая модель нейрона
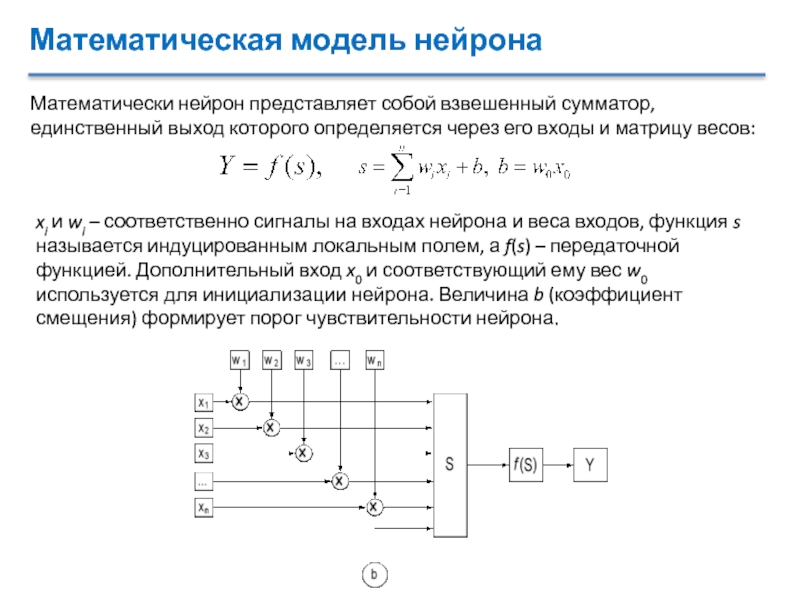
Математически нейрон представляет собой взвешенный сумматор, единственный выход
которого определяется через его входы и матрицу весов:
.
xi и
wi – соответственно сигналы на входах нейрона и веса входов, функция s называется индуцированным локальным полем, а f(s) – передаточной функцией. Дополнительный вход x0 и соответствующий ему вес w0 используется для инициализации нейрона. Величина b (коэффициент смещения) формирует порог чувствительности нейрона.Слайд 13Передаточные функции искусственных нейронов
.
Другие примеры:
Экспонента
Тригонометрический синус
Модульная
Квадратичная
Радиально-базисная
Гиперболический тангенс
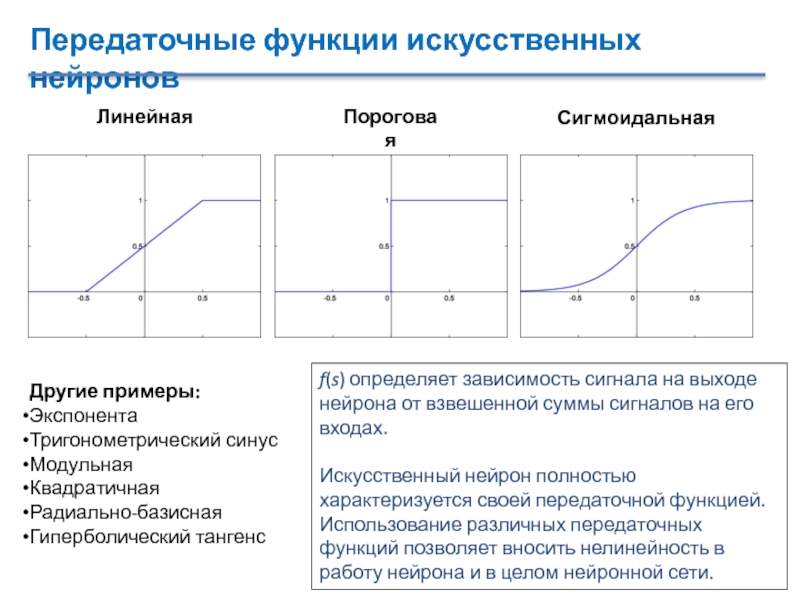
f(s) определяет зависимость
сигнала на выходе нейрона от взвешенной суммы сигналов на его
входах.Искусственный нейрон полностью характеризуется своей передаточной функцией. Использование различных передаточных функций позволяет вносить нелинейность в работу нейрона и в целом нейронной сети.
Слайд 14Принципы функционирования ИНС
Действующие параллельно и соединенные последовательно искусственные нейроны составляют
основу нейронной сети.
Как и в природе, функция нейронной сети в
значительной степени определяется связями между элементами. Регулируя значения коэффициентов (весов) связи нейронную сеть можно настраивать (обучать) для выполнения конкретной функции.Искусственные нейронные сети настраиваются или обучаются так, чтобы конкретные входы преобразовывались в заданный целевой выход. Сеть обучается, основываясь на сравнении сигналов выхода и цели до тех пор, пока выход сети не будет соответствовать, т.е. близок к цели.
Чтобы обучить сеть при таком управляемом обучении, как правило, используется много пар значений сигналов вход/цель.
.
Слайд 15Преимущества нейросетевого подхода
Решение задач, не поддающихся адекватной формализации традиционными аналитическими
методами, поскольку невозможно учесть все особенности описываемого процесса.
Решение формализуемых задач,
для которых в настоящее время отсутствует математический аппарат решения.Решение формализуемых задач с существующим математическим аппаратом для их решения, но реализация вычислений с его помощью не удовлетворяет требованиям по затрачиваемым вычислительным ресурсам.
Получение неявной модели системы без построения ее конкретного физического представления, используя только достаточно большие массивы экспериментальных данных.
Создание ИНС с учетом физических представлений об изучаемых причинно-следственных связях в рассматриваемом процессе. Сочетание корреляционной обработки изучаемых сигналов с их нелинейным преобразованием.
.
Слайд 16Основные направления использования
.
1) Восстановление образов, прогнозирование состояния системы
Выяснение зависимости
между группами последовательных данных, находящихся в причинно-следственной связи.
ИНС необходимы для
«обучения» образцы – набор пар вход/цель. Таким образом реализуется схема обучения «С учителем».2) Классификация образов
Объединение данных в группы по схожим признакам и выделение характерных особенностей изучаемых явлений на этой основе.
ИНС необходимо для «обучения» только «знать» количество классов. Таким образом реализуется схема обучения «Без учителя» – ИНС выступает в роли эксперта.
Слайд 17Проблема синтеза ИНС
Задача синтеза требуемой искусственной сети - общая проблема
кибернетики, заключающаяся в построении искусственной системы с заданным функциональным поведением.
Стандартные
этапы решения этой проблемы следующие:выбор существенных для решаемой задачи признаков и формирование признаковых пространств
выбор или разработка архитектуры нейронной сети, адекватной решаемой задаче
получение обучающей выборки из наиболее представительных векторов признаковых пространств
обучение нейронной сети на обучающей выборке
Слайд 18Алгоритмы обучения нейросетей
Процесс (алгоритм) обучения нейронной сети предполагает следующую последовательность
событий:
В нейронную сеть поступают стимулы из внешней среды
Изменяются свободные параметры
нейронной сети (веса и смещения связей нейронов).После изменения параметров нейронная сеть отвечает на поступающие стимулы уже иным образом.
Не существует универсального алгоритма обучения, подходящего для всех нейронных сетей. Существует лишь набор средств, представленный множеством алгоритмов обучения, каждый из которых имеет свои достоинства и недостатки.
Необходимо найти оптимальные значения всех переменных весовых коэффициентов. От того, с каким качеством выполнен их поиск, зависит способность ИНС решать поставленные задачи.
Слайд 19Свойства успешно обученных ИНС
Обучаемость/дообучаемость. Выбрав одну из моделей ИНС, создав
сеть и выполнив алгоритм обучения, мы можем обучить сеть решению
задачи, которая ей по силам. Нет никаких гарантий, что это удастся сделать при выборе архитектуры данной сети, алгоритме и задаче, но если все сделано правильно, то обучение будет успешным.Способность к обобщению. После обучения сеть становится нечувствительной к малым изменениям входных сигналов (шуму или вариациям входных образов) и дает правильный результат на выходе.
Способность к абстрагированию. Если предъявить сети несколько искаженных вариантов входного образа, то сеть сама может создать на выходе идеальный образ, с которым она никогда не встречалась.
Слайд 20Обучение «С учителем»
Путем анализа имеющихся входных/выходных данных, веса и смещения
сети автоматически настраиваются так, чтобы минимизировать разность между желаемым сигналом
и сигналом, полученным на выходе в результате работы сети. Эта разность – ошибка обучения.Ошибка обучения для конкретной конфигурации ИНС определяется путем прогона через сеть всех имеющихся наблюдений и сравнения выходных значений с желаемыми, целевыми значениями.
Эти разности позволяют сформировать так называемую функцию ошибок (критерий качества обучения). В качестве такой функции чаще всего берется сумма квадратов ошибок.
При моделировании ИНС с линейными функциями активации нейронов гарантируется достижение абсолютного минимума ошибки обучения.
Для ИНС с нелинейными функциями активации нельзя гарантировать достижения глобального минимума функции ошибки.
Слайд 21Пример №1 – Решение не найдено
(градиентный метод наискорейшего спуска)
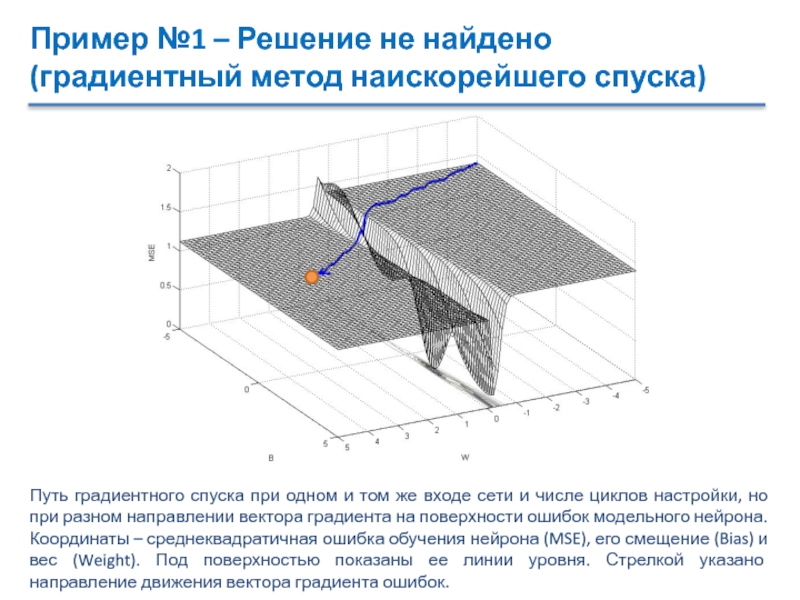
Путь градиентного
спуска при одном и том же входе сети и числе
циклов настройки, но при разном направлении вектора градиента на поверхности ошибок модельного нейрона. Координаты – среднеквадратичная ошибка обучения нейрона (MSE), его смещение (Bias) и вес (Weight). Под поверхностью показаны ее линии уровня. Стрелкой указано направление движения вектора градиента ошибок.
Слайд 22Пример №2 – Достигнут локальный минимум
Путь градиентного спуска при одном
и том же входе сети и числе циклов настройки, но
при разном направлении вектора градиента на поверхности ошибок модельного нейрона. Координаты – среднеквадратичная ошибка обучения нейрона (MSE), его смещение (Bias) и вес (Weight). Под поверхностью показаны ее линии уровня. Стрелкой указано направление движения вектора градиента ошибок.
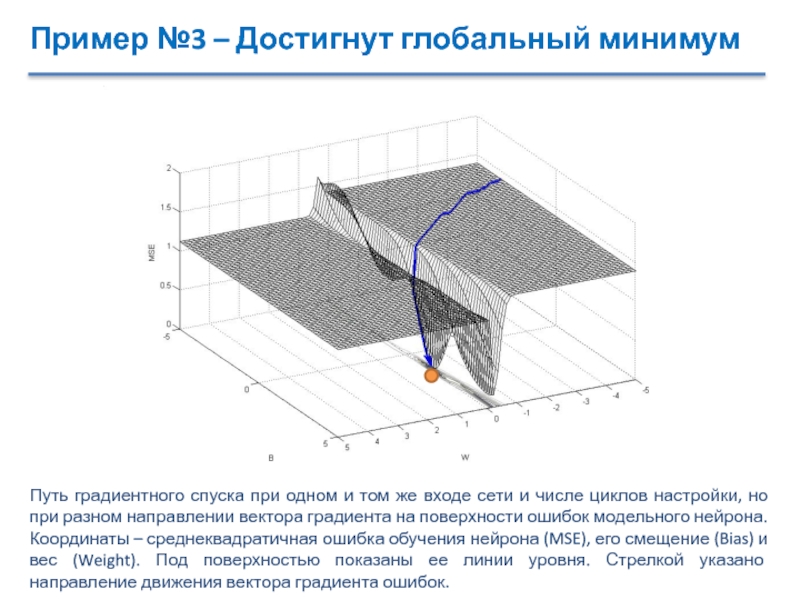
Слайд 23Пример №3 – Достигнут глобальный минимум
Путь градиентного спуска при одном
и том же входе сети и числе циклов настройки, но
при разном направлении вектора градиента на поверхности ошибок модельного нейрона. Координаты – среднеквадратичная ошибка обучения нейрона (MSE), его смещение (Bias) и вес (Weight). Под поверхностью показаны ее линии уровня. Стрелкой указано направление движения вектора градиента ошибок.
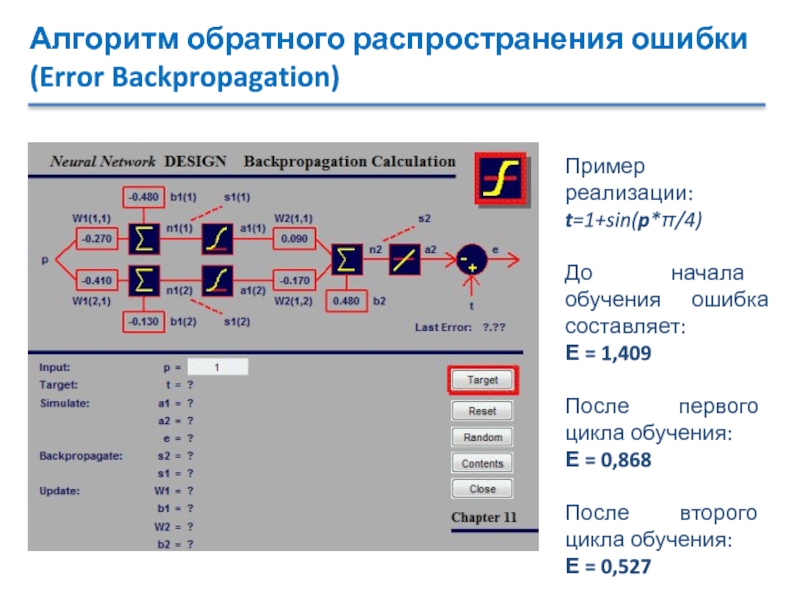
Слайд 24Алгоритм обратного распространения ошибки
(Error Backpropagation)
Пример реализации:
t=1+sin(p*π/4)
До начала обучения ошибка составляет:
Е
= 1,409
После первого цикла обучения:
Е = 0,868
После второго цикла обучения:
Е
= 0,527Слайд 25Обучение «Без учителя»
Система обучается установлению принадлежности образа к одному из
формально определенных классов.
Формальные признаки могут быть определены посредством простых правил
типа «если… – то...».Задачей системы является формирование обобщающих признаков в совокупности примеров. При увеличении числа примеров несущественные, случайные признаки сглаживаются, а часто встречающиеся усиливаются, при этом происходит постепенное уточнение границ категорий.
Хорошо обученная нейросетевая система способна извлекать признаки из новых примеров, ранее неизвестных системе, и принимать на их основе приемлемые решения.
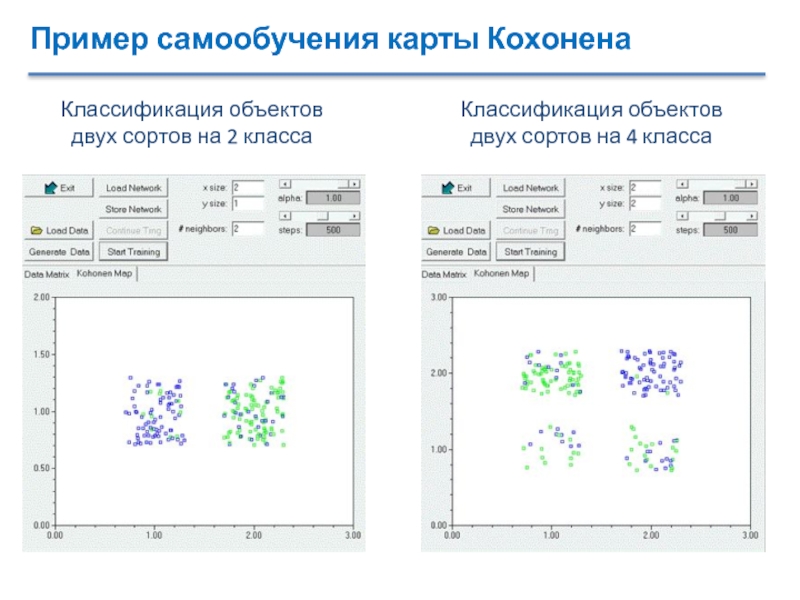
Слайд 26Пример самообучения карты Кохонена
Классификация объектов
двух сортов на 2 класса
Классификация объектов
двух
сортов на 4 класса
Слайд 27Области применения ИНС
Прогнозирование и восстановление числовых рядов
Кластерный анализ
Классификация и распознавание
образов
Обработка изображений
Нелинейное управление процессами
Адаптивная фильтрация
Финансовое прогнозирование
Сжатие и шифрование информации
Параллельные вычисления
на суперкомпьютерах (Blue Brain Project, Blue Gene)В настоящее время метод ИНС активно применяется в гелиогеофизике для решения задач прогноза параметров солнечно-земных связей и различных геофизических явлений.
Слайд 28Решение задач прогнозирования и
восстановления рядов данных
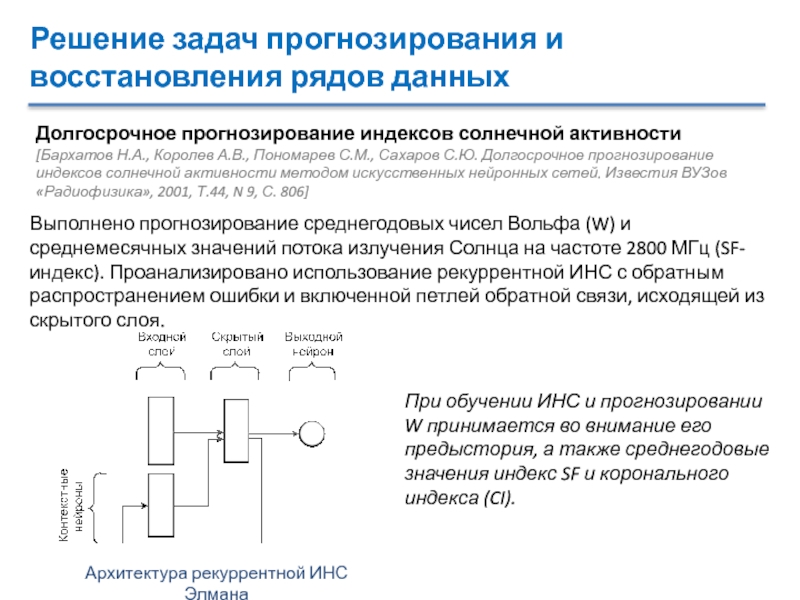
Долгосрочное прогнозирование индексов солнечной активности
[Бархатов
Н.А., Королев А.В., Пономарев С.М., Сахаров С.Ю. Долгосрочное прогнозирование индексов
солнечной активности методом искусственных нейронных сетей. Известия ВУЗов «Радиофизика», 2001, Т.44, N 9, С. 806]Выполнено прогнозирование среднегодовых чисел Вольфа (W) и среднемесячных значений потока излучения Солнца на частоте 2800 МГц (SF-индекс). Проанализировано использование рекуррентной ИНС с обратным распространением ошибки и включенной петлей обратной связи, исходящей из скрытого слоя.
Архитектура рекуррентной ИНС Элмана
При обучении ИНС и прогнозировании W принимается во внимание его предыстория, а также среднегодовые значения индекс SF и коронального индекса (CI).
Слайд 29Решение задач прогнозирования и
восстановления рядов данных
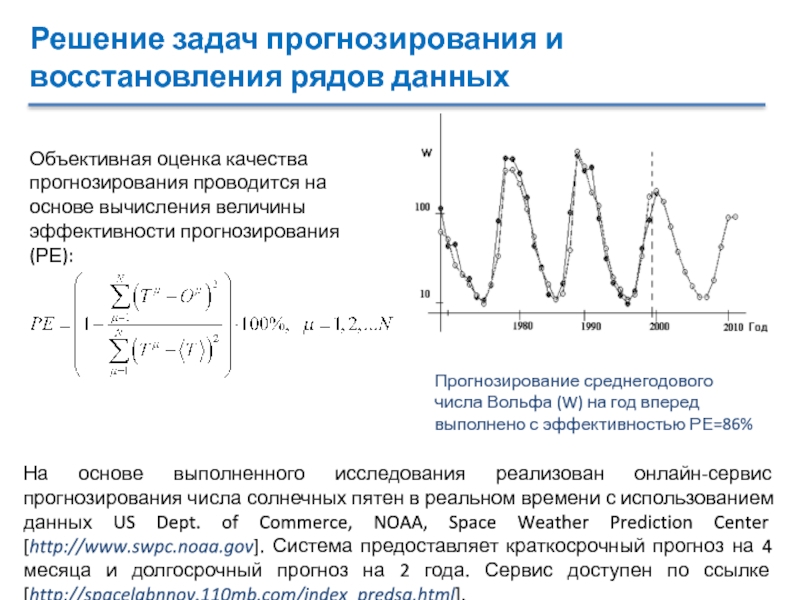
Объективная оценка качества прогнозирования проводится
на основе вычисления величины эффективности прогнозирования (РЕ):
Прогнозирование среднегодового числа Вольфа
(W) на год вперед выполнено с эффективностью РЕ=86%На основе выполненного исследования реализован онлайн-сервис прогнозирования числа солнечных пятен в реальном времени с использованием данных US Dept. of Commerce, NOAA, Space Weather Prediction Center [http://www.swpc.noaa.gov]. Система предоставляет краткосрочный прогноз на 4 месяца и долгосрочный прогноз на 2 года. Сервис доступен по ссылке [http://spacelabnnov.110mb.com/index_predsa.html].
Слайд 30Решение задач прогнозирования и
восстановления рядов данных
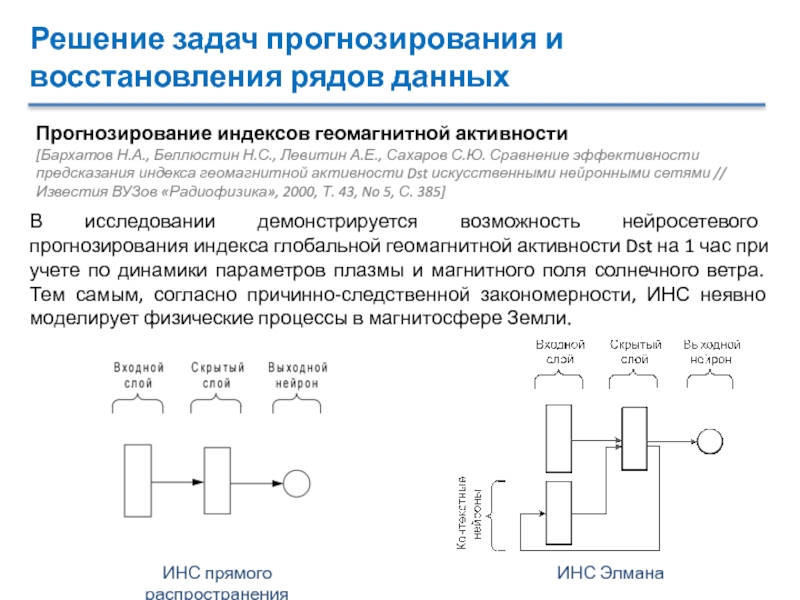
Прогнозирование индексов геомагнитной активности
[Бархатов Н.А.,
Беллюстин Н.С., Левитин А.Е., Сахаров С.Ю. Сравнение эффективности предсказания индекса
геомагнитной активности Dst искусственными нейронными сетями // Известия ВУЗов «Радиофизика», 2000, Т. 43, No 5, С. 385]В исследовании демонстрируется возможность нейросетевого прогнозирования индекса глобальной геомагнитной активности Dst на 1 час при учете по динамики параметров плазмы и магнитного поля солнечного ветра. Тем самым, согласно причинно-следственной закономерности, ИНС неявно моделирует физические процессы в магнитосфере Земли.
ИНС Элмана
ИНС прямого распространения
Слайд 31Решение задач прогнозирования и
восстановления рядов данных
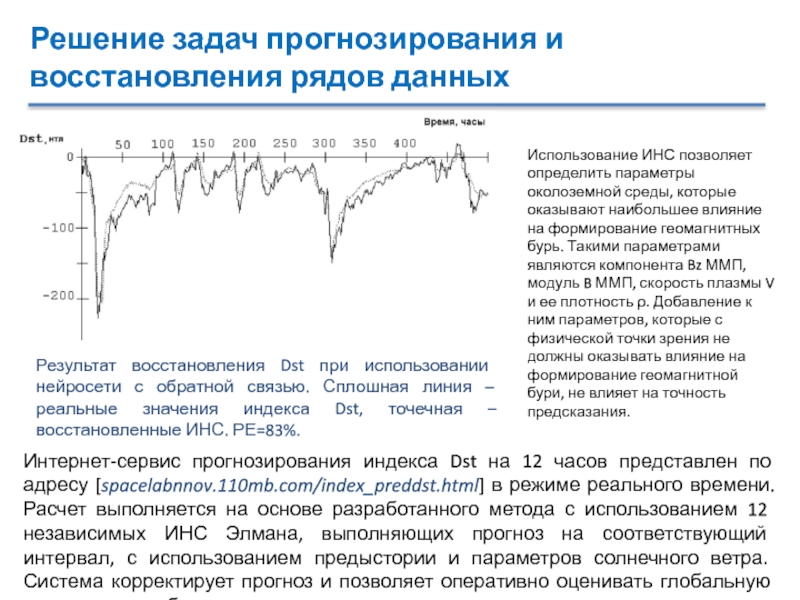
Использование ИНС позволяет определить параметры
околоземной среды, которые оказывают наибольшее влияние на формирование геомагнитных бурь.
Такими параметрами являются компонента Bz ММП, модуль B ММП, скорость плазмы V и ее плотность ρ. Добавление к ним параметров, которые с физической точки зрения не должны оказывать влияние на формирование геомагнитной бури, не влияет на точность предсказания.Результат восстановления Dst при использовании нейросети с обратной связью. Сплошная линия – реальные значения индекса Dst, точечная – восстановленные ИНС. РЕ=83%.
Интернет-сервис прогнозирования индекса Dst на 12 часов представлен по адресу [spacelabnnov.110mb.com/index_preddst.html] в режиме реального времени. Расчет выполняется на основе разработанного метода с использованием 12 независимых ИНС Элмана, выполняющих прогноз на соответствующий интервал, с использованием предыстории и параметров солнечного ветра. Система корректирует прогноз и позволяет оперативно оценивать глобальную геомагнитную обстановку.
Слайд 32Решение задач прогнозирования и
восстановления рядов данных
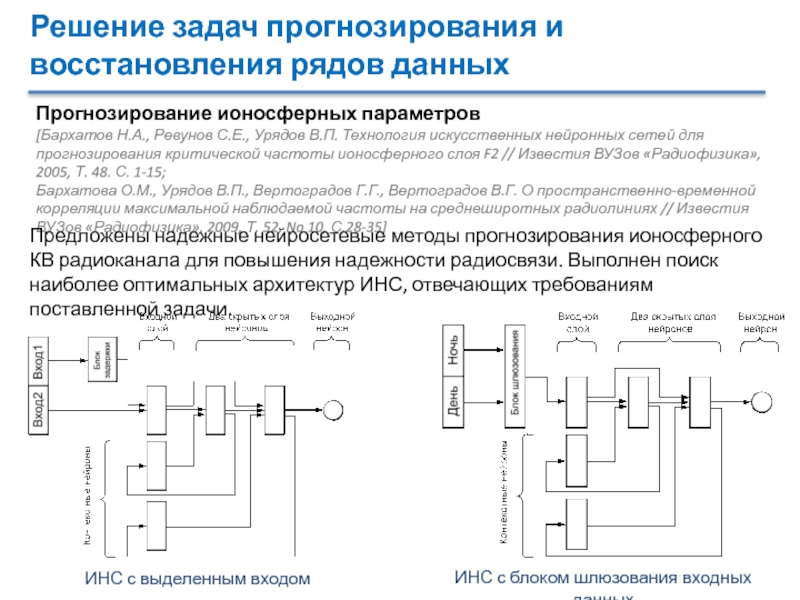
Прогнозирование ионосферных параметров
[Бархатов Н.А., Ревунов
С.Е., Урядов В.П. Технология искусственных нейронных сетей для прогнозирования критической
частоты ионосферного слоя F2 // Известия ВУЗов «Радиофизика», 2005, Т. 48. С. 1-15;Бархатова О.М., Урядов В.П., Вертоградов Г.Г., Вертоградов В.Г. О пространственно-временной корреляции максимальной наблюдаемой частоты на среднеширотных радиолиниях // Известия ВУЗов «Радиофизика», 2009, Т. 52, No 10, С.28-35]
Предложены надежные нейросетевые методы прогнозирования ионосферного КВ радиоканала для повышения надежности радиосвязи. Выполнен поиск наиболее оптимальных архитектур ИНС, отвечающих требованиям поставленной задачи.
ИНС с выделенным входом
ИНС с блоком шлюзования входных данных
Слайд 33Решение задач прогнозирования и
восстановления рядов данных
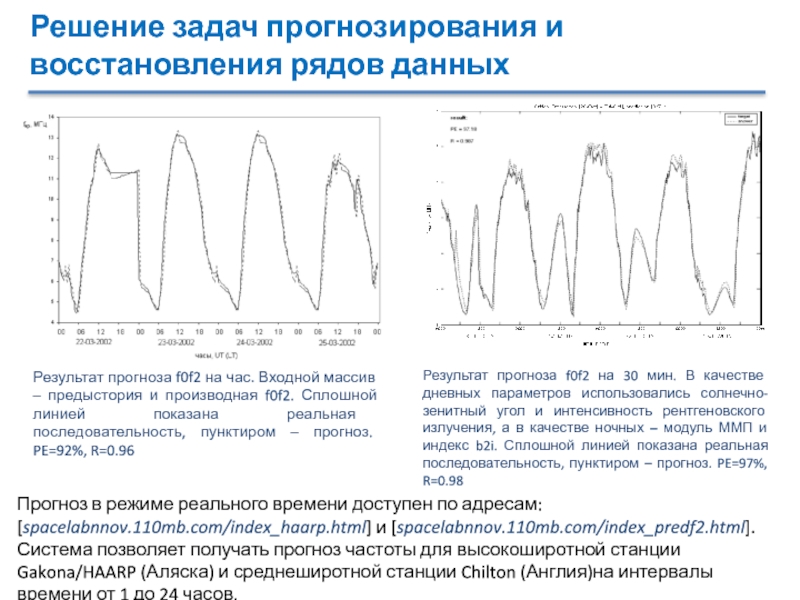
Результат прогноза f0f2 на час.
Входной массив – предыстория и производная f0f2. Сплошной линией показана
реальная последовательность, пунктиром – прогноз. PE=92%, R=0.96Результат прогноза f0f2 на 30 мин. В качестве дневных параметров использовались солнечно-зенитный угол и интенсивность рентгеновского излучения, а в качестве ночных – модуль ММП и индекс b2i. Сплошной линией показана реальная последовательность, пунктиром – прогноз. PE=97%, R=0.98
Прогноз в режиме реального времени доступен по адресам:
[spacelabnnov.110mb.com/index_haarp.html] и [spacelabnnov.110mb.com/index_predf2.html].
Система позволяет получать прогноз частоты для высокоширотной станции Gakona/HAARP (Аляска) и среднеширотной станции Chilton (Англия)на интервалы времени от 1 до 24 часов.
Слайд 34Решение задач классификации образов
Многопараметрическая классификация последствий солнечной активности
[Бархатов Н.А., Левитин
А.Е., Ревунова Е.А. Классификация комплексов космической погоды с учетом характеристик
плазменного потока из солнечного источника // Геомагнетизм и аэрономия, на рецензии]Разработана техника классификации комплексов космической погоды, включающей в себя образы характеристик возмущенного солнечного потока (параметры солнечного ветра и компоненты межпланетного магнитного поля) с учетом типа его солнечного источника и его геомагнитного проявления в форме Dst-индекса.
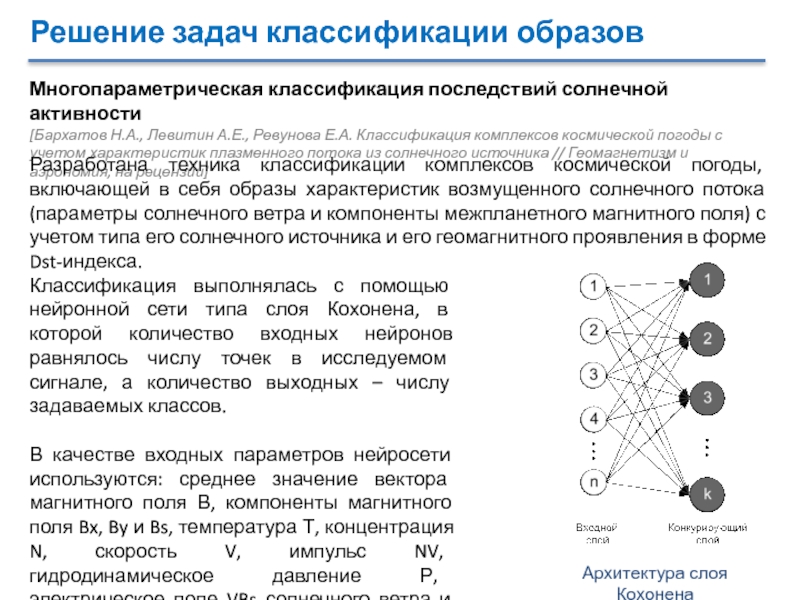
Классификация выполнялась с помощью нейронной сети типа слоя Кохонена, в которой количество входных нейронов равнялось числу точек в исследуемом сигнале, а количество выходных – числу задаваемых классов.
В качестве входных параметров нейросети используются: среднее значение вектора магнитного поля В, компоненты магнитного поля Bx, By и Bs, температура Т, концентрация N, скорость V, импульс NV, гидродинамическое давление Р, электрическое поле VBs солнечного ветра и Dst-индекс.
Архитектура слоя Кохонена
Слайд 35Решение задач классификации образов
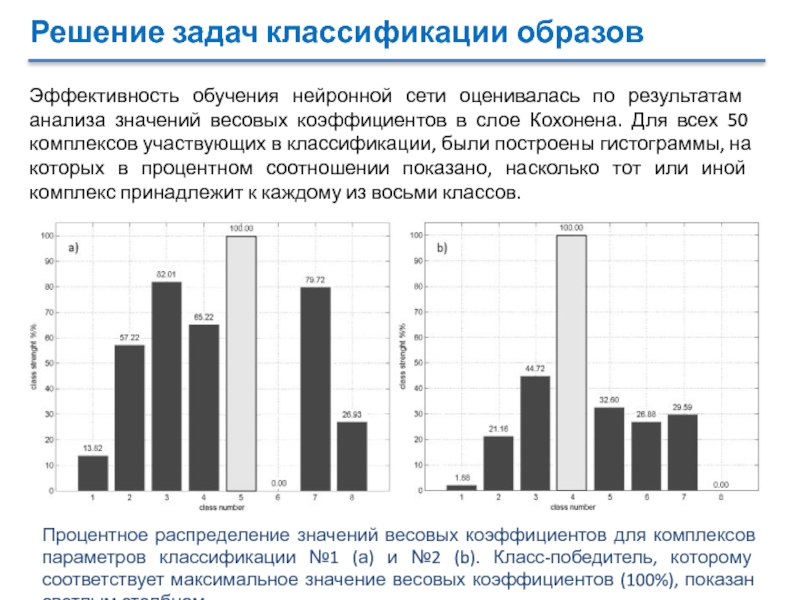
Эффективность обучения нейронной сети оценивалась по результатам
анализа значений весовых коэффициентов в слое Кохонена. Для всех 50
комплексов участвующих в классификации, были построены гистограммы, на которых в процентном соотношении показано, насколько тот или иной комплекс принадлежит к каждому из восьми классов.Процентное распределение значений весовых коэффициентов для комплексов параметров классификации №1 (а) и №2 (b). Класс-победитель, которому соответствует максимальное значение весовых коэффициентов (100%), показан светлым столбцом.
Слайд 36Решение задач классификации образов
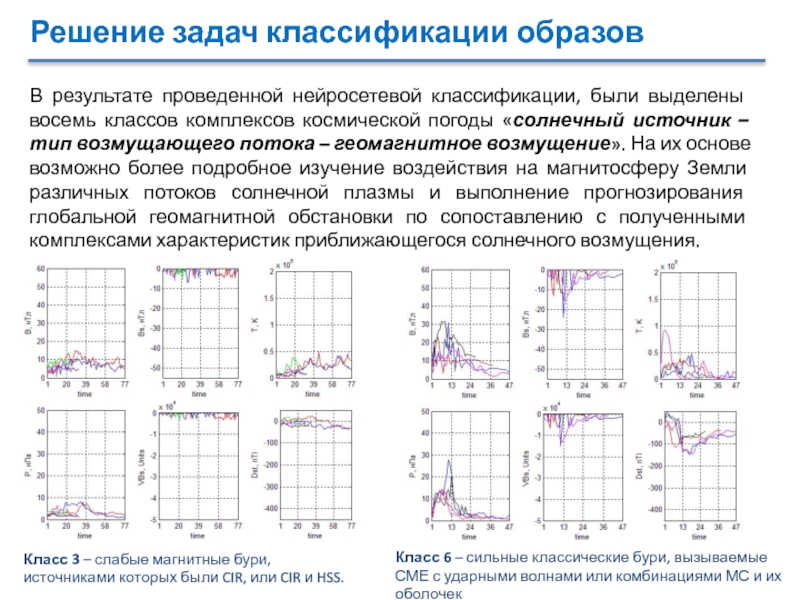
В результате проведенной нейросетевой классификации, были выделены
восемь классов комплексов космической погоды «солнечный источник – тип возмущающего
потока – геомагнитное возмущение». На их основе возможно более подробное изучение воздействия на магнитосферу Земли различных потоков солнечной плазмы и выполнение прогнозирования глобальной геомагнитной обстановки по сопоставлению с полученными комплексами характеристик приближающегося солнечного возмущения.Класс 6 – сильные классические бури, вызываемые СМЕ с ударными волнами или комбинациями МС и их оболочек
Класс 3 – слабые магнитные бури, источниками которых были CIR, или CIR и HSS.
Слайд 37Другие решенные задачи с применением ИНС
Восстановление пробелов в записях отдельных
магнитных обсерваторий по данным других станций
Пересчет современных индексов полярной активности
к классическимВзаимное восстановление индексов AU/AL и ASY/SYM при учете параметров околоземного пространства
Космическая классификация глобальных геомагнитных возмущений
Классификация разрывов параметров космической плазмы
Контроль пространственной динамики полярной шапки и полярного овала по данным гренландской сети магнитных станций
Анализ связи магнитных возмущений в авроральной области и магнитного возмущения на средних и низких широтах
Слайд 38Подробнее о технологии ИНС в геофизике
История развития технологии ИНС
Математические модели
нейронов и нейросетей
Теоретические обоснования возможности создания ИНС
Способы представления информации в
нейронных сетяхНечеткие нейронные сети
Применение ИНС в задачах солнечно-земной физики
Слайд 39Интернет-сервисы на основе технологии ИНС в режиме реального времени
Моделирование причинно-следственных
связей в гелиогеофизических задачах в режиме реального времени с помощью
нейросетевого программно-вычислительного интернет-комплексаПрогноз Dst-индекса глобальной геомагнитной активности в реальном времени на 12 часов.
Прогноз критической частоты ионосферного слоя F2 на 24 часа
Краткосрочный прогноз на 4 месяца и долгосрочный прогноз на 2 года числа солнечных пятен в реальном времени
Нейросетевое восстановление классических индексов АЕ(12) полярных электроджетов
spacelabnnov.110mb.com