Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Непараметрические критерии
Содержание
- 1. Непараметрические критерии
- 2. Параметрические и непараметрические критерииРассмотренные ранее статистические критерии
- 3. Понятие ранга наблюденияВсе непараметрические критерии используют понятие
- 4. ПримерИмеются баллы, полученные 10 студентами на экзамене.
- 5. ПримерИмеются баллы, полученные 10 студентами на экзамене.
- 6. ПримерПредположим, что некоторые числа повторяются. Например,25, 37,
- 7. ПримерПредположим, что некоторые числа повторяются. Например,25, 37,
- 8. Однофакторный непараметрический критерий Краскела-УоллисаKruskal-Wallis Test
- 9. Пример данныхИмеется ли разница в среднем возрасте
- 10. Критерий Краскела-УоллисаВ дисперсионном анализе используется F-критерий, чтобы
- 11. Условия примененияВыборки независимы и получены случайным образом.Размер каждой выборки должен быть не меньше пяти.
- 12. Суть критерия1. В критерии Краскела–Уоллиса все выборки
- 13. Вычисления в таблице
- 14. Вычисления в таблице
- 15. Вычисления в таблице
- 16. Вычисления в таблице
- 17. Вычисления в таблице
- 18. Вычисления в таблице
- 19. Вычисления в таблице
- 20. Вычисления в таблице
- 21. Вычисления в таблице
- 22. Вычисления в таблице
- 23. Вычисления в таблице
- 24. Вычисления в таблице
- 25. Вычисления в таблице
- 26. Вычисления в таблице
- 27. Вычисления в таблице
- 28. Вычисления в таблице
- 29. СтатистикаФормула статистики Краскела-Уоллиса: где: – средние ранги
- 30. Вычисляем значение статистики
- 31. Критическая областьКритерий использует правостороннюю критическую область. Критическое значение определяем с помощью функцию Excel=ХИ2ОБР(α;k-1)2(; k -1)
- 32. Находим границу критической областиСнова воспользуемся таблицами EXCEL
- 33. Сравниваем и делаем выводПолученное значение статистики не
- 34. 9.3. Коэффициент корреляции Спирмена
- 35. Постановка задачиПредположим, что для n объектов известны
- 36. Постановка задачиПредположим, что для n объектов известны
- 37. Понятие рангового коэффициента корреляции- ранги объектов по
- 38. Коэффициент ранговой корреляции Спирмена можно вычислить и по более простой формуле:
- 39. Свойства рангового коэффициента корреляции1. Еслигде f – возрастающая функция, то r =1.
- 40. Свойства рангового коэффициента корреляции2. Еслигде f – убывающая функция, то r =-1.
- 41. пример.Вычислить коэффициент ранговой корреляции между результатами теста по математике и статистике
- 42. пример
- 43. пример
- 44. пример
- 45. пример
- 46. пример
- 47. Проверка значимости рангового коэффициента корреляцииОбозначения:Выборочный коэффициент корреляции
- 48. Проверка значимости рангового коэффициента корреляцииЕсли исходные порядковые
- 49. Проверка значимости рангового коэффициента корреляцииПроверим значимость
- 50. Проверка значимости рангового коэффициента корреляцииПроверим значимость
- 51. Проверка значимости рангового коэффициента корреляцииПроверим значимость=СТЬЮДРАСПОБР(0,05;8-2)2.45
- 52. Проверка значимости рангового коэффициента корреляцииПроверим значимость=СТЬЮДРАСПОБР(0,05;8-2)2.45Принимаем гипотезу
- 53. Пример. Конкурс красотыДва эксперта - мужчина и
- 54. Пример. Конкурс красотыДва эксперта - мужчина и
- 55. Решение. Вычисляем коэффициент ранговой корреляции Спирмена:
- 56. Решение. Вычисляем коэффициент ранговой корреляции Спирмена:Вычисляем статистику
- 57. Решение. Находим критическое значениеПолучим 2,3Критическая область задается
- 58. Решение в Excel Критерий Краскелла-Уоллиса Имеется ли
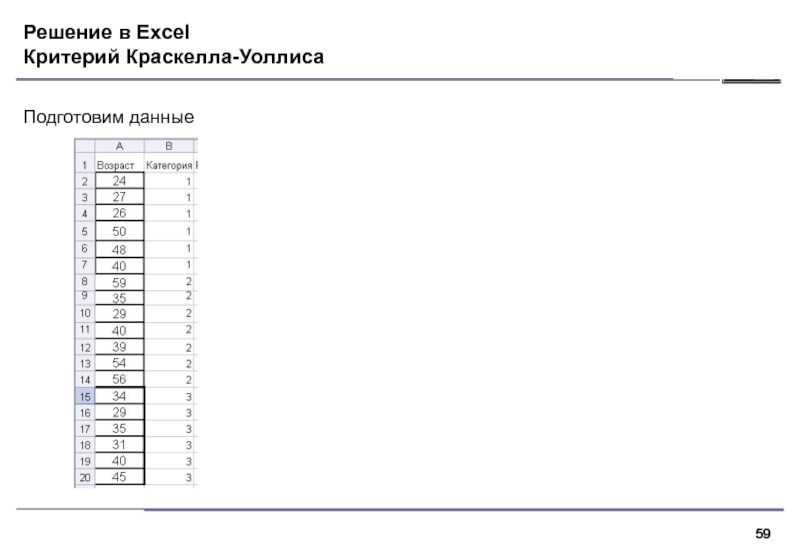
- 59. Решение в Excel Критерий Краскелла-Уоллиса Подготовим данные
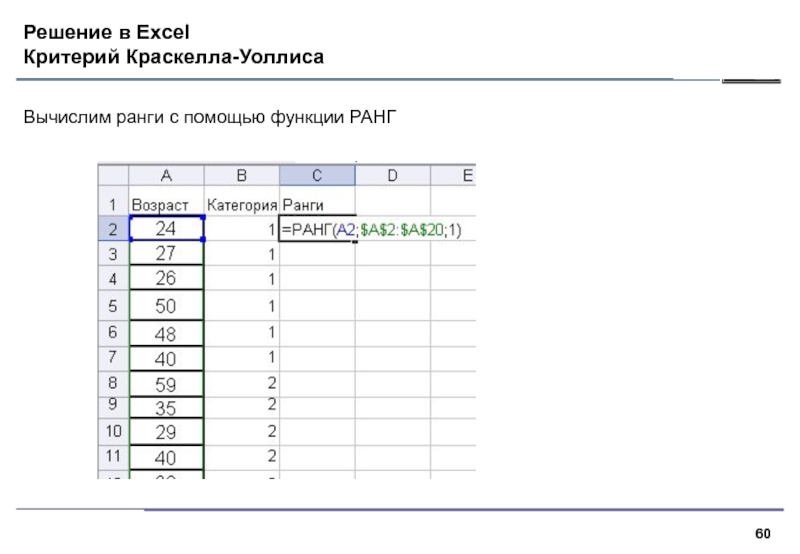
- 60. Решение в Excel Критерий Краскелла-Уоллиса Вычислим ранги с помощью функции РАНГ
- 61. Решение в Excel Критерий Краскелла-Уоллиса Вычислим ранги
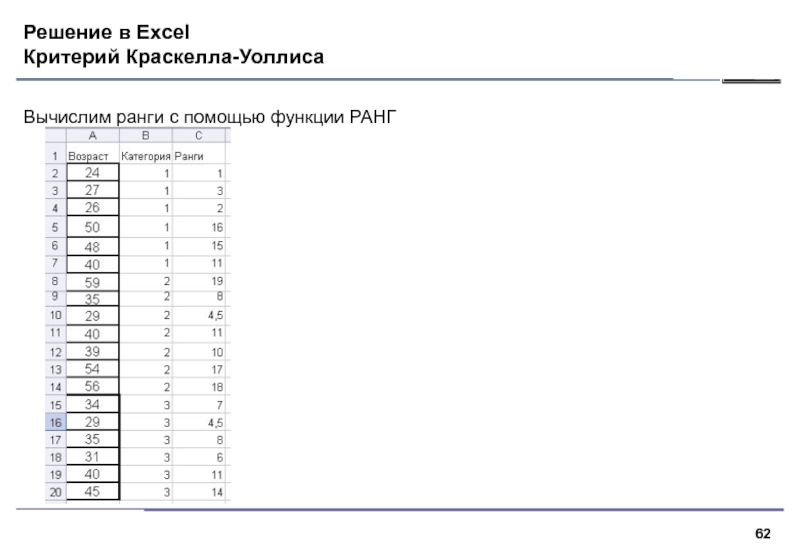
- 62. Решение в Excel Критерий Краскелла-Уоллиса Вычислим ранги с помощью функции РАНГ
- 63. Решение в Excel Критерий Краскелла-Уоллиса Вычислим ранги с помощью функции РАНГ
- 64. Решение в Excel Критерий Краскелла-Уоллиса Начиная с EXCEL 2010 появилась функция РАНГ.СР, которая вычисляет ранги корректно
- 65. Решение в Excel Критерий Краскелла-Уоллиса
- 66. Решение в Excel Критерий Краскелла-Уоллиса
- 67. Решение в Excel Критерий Краскелла-Уоллиса
- 68. Решение в Excel Критерий Краскелла-Уоллиса
- 69. Решение в Excel Критерий Краскелла-Уоллиса
- 70. Скачать презентанцию
Параметрические и непараметрические критерииРассмотренные ранее статистические критерии были параметрическими. Параметрические критерии предназначены для проверки гипотез о параметрах генеральной совокупности с нормальным распределением.Непараметрические критерии используют для исследования генеральных совокупностей, которые не распределены
Слайды и текст этой презентации
Слайд 1
Непараметрические критерии.
9.1 Однофакторный непараметрический анализ. Критерий Краскела-Уоллиса
9.2 Ранговая корреляция.
Коэффициент Спирмена
Слайд 2Параметрические и непараметрические критерии
Рассмотренные ранее статистические критерии были параметрическими. Параметрические
критерии предназначены для проверки гипотез о параметрах генеральной совокупности с
нормальным распределением.Непараметрические критерии используют для исследования генеральных совокупностей, которые не распределены нормально.
Слайд 3Понятие ранга наблюдения
Все непараметрические критерии используют понятие ранга.
Ранг – это
порядковый номер наблюдения в вариационном ряду (упорядоченной по возрастанию выборке).
Слайд 4Пример
Имеются баллы, полученные 10 студентами на экзамене. Найти ранги.
25, 37,
90, 68, 5, 76, 45, 10, 69, 51
Слайд 5Пример
Имеются баллы, полученные 10 студентами на экзамене. Найти ранги.
25, 37,
90, 68, 5, 76, 45, 10, 69, 51
Слайд 6Пример
Предположим, что некоторые числа повторяются. Например,
25, 37, 90, 68, 5,
76, 45, 10, 68, 51. Тогда каждому из совпадающих элементов
приписывается ранг, равный среднему арифметическому их порядковых номеров в вариационном ряду
Слайд 7Пример
Предположим, что некоторые числа повторяются. Например,
25, 37, 90, 68, 5,
68, 45, 10, 68, 51. Тогда каждому из совпадающих элементов
приписывается ранг, равный среднему арифметическому их порядковых номеров в вариационном ряду
Слайд 9Пример данных
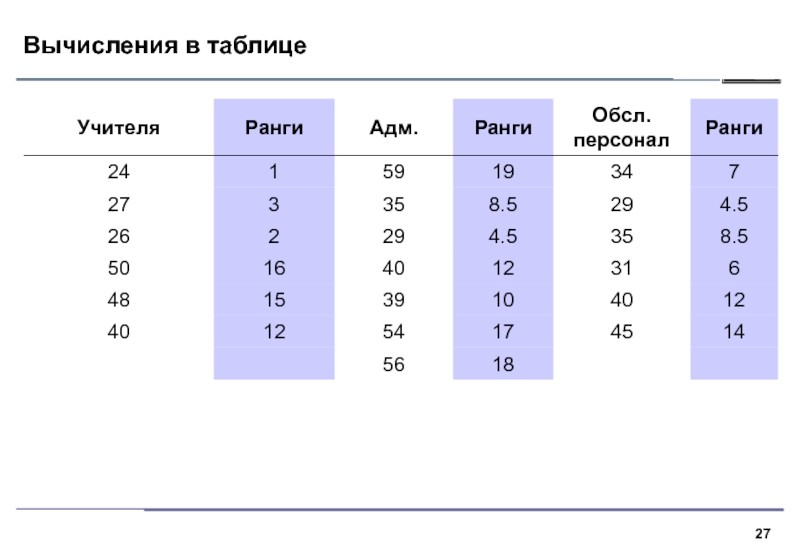
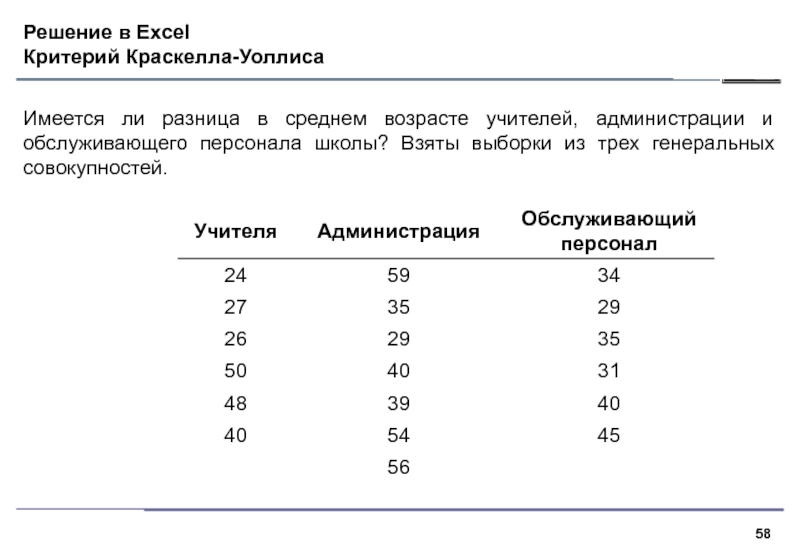
Имеется ли разница в среднем возрасте учителей, администрации и
обслуживающего персонала школы? Взяты выборки из трех генеральных совокупностей.
Слайд 10Критерий Краскела-Уоллиса
В дисперсионном анализе используется F-критерий, чтобы сравнивать средние трех
и более совокупностей. Для критерия ANOVA предполагается, что совокупности нормально
распределены. Когда это условие не выполняется, то для сравнения средних может использоваться непараметрический критерий Краскeла–Уоллиса.Критерий Краскела-Уоллиса – непараметрический тест, который использует ранги трех и более независимых выборок. Применяется для проверки гипотезы о том, что выборки получены из генеральных совокупностей, имеющих одинаковый закон распределения:
H0: распределения генеральных совокупностей совпадают
H1: распределения отличаются
Слайд 11Условия применения
Выборки независимы и получены случайным образом.
Размер каждой выборки должен
быть не меньше пяти.
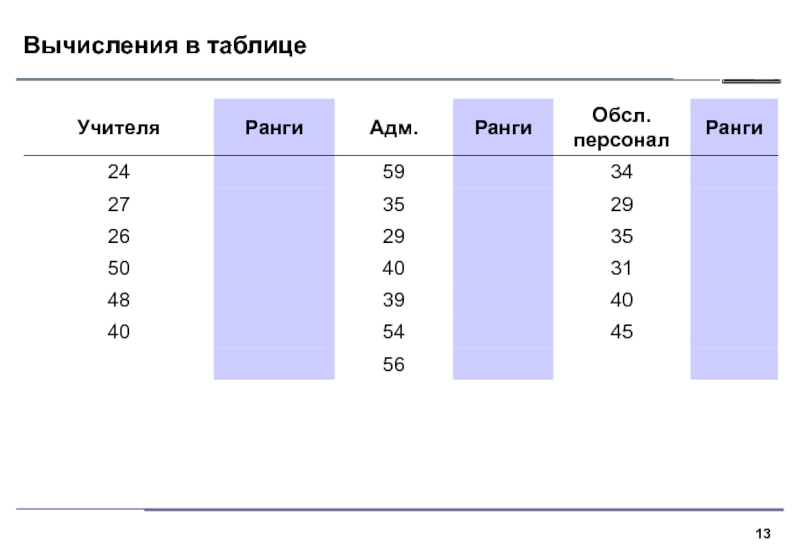
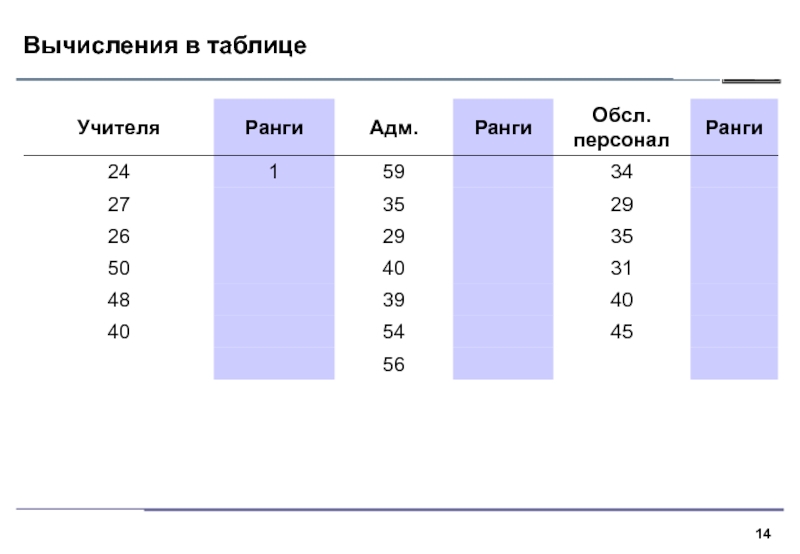
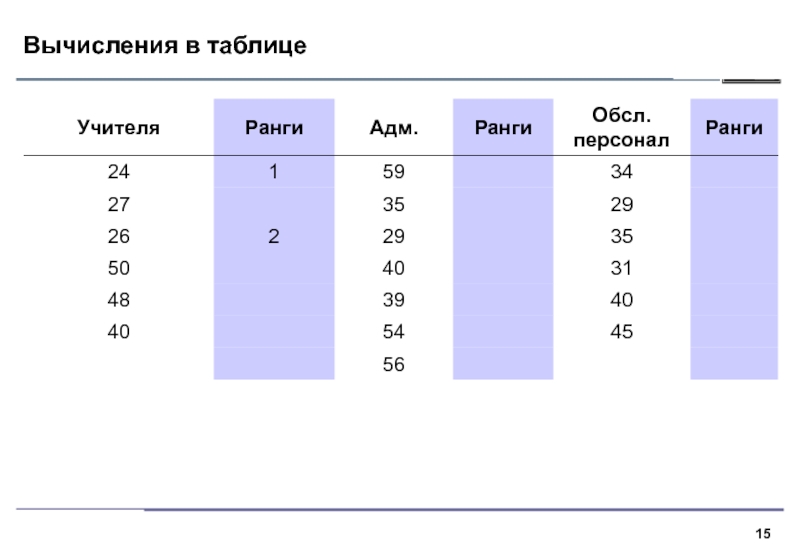
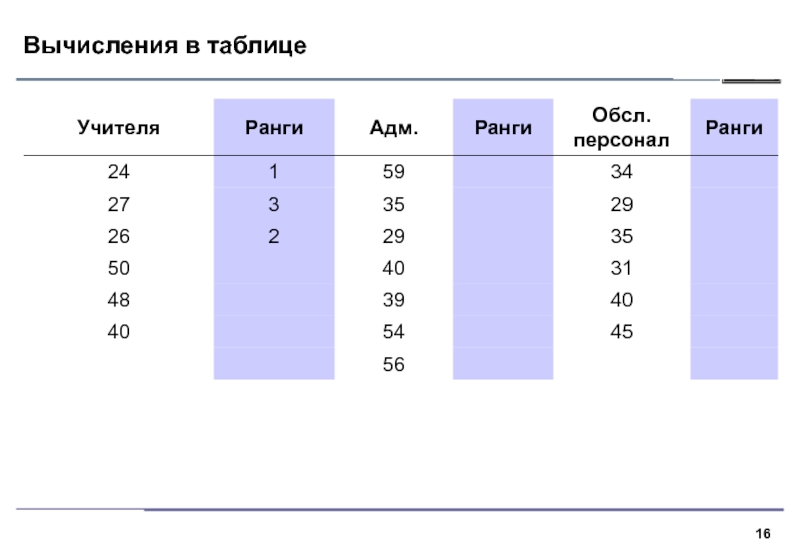
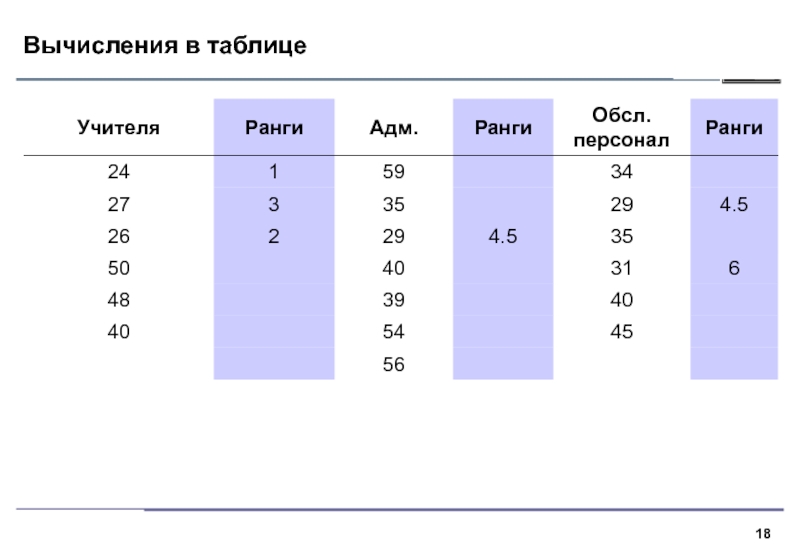
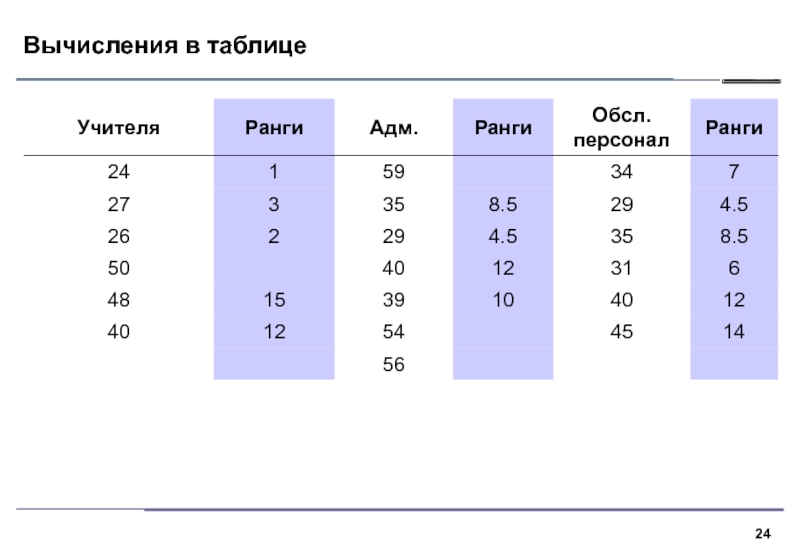
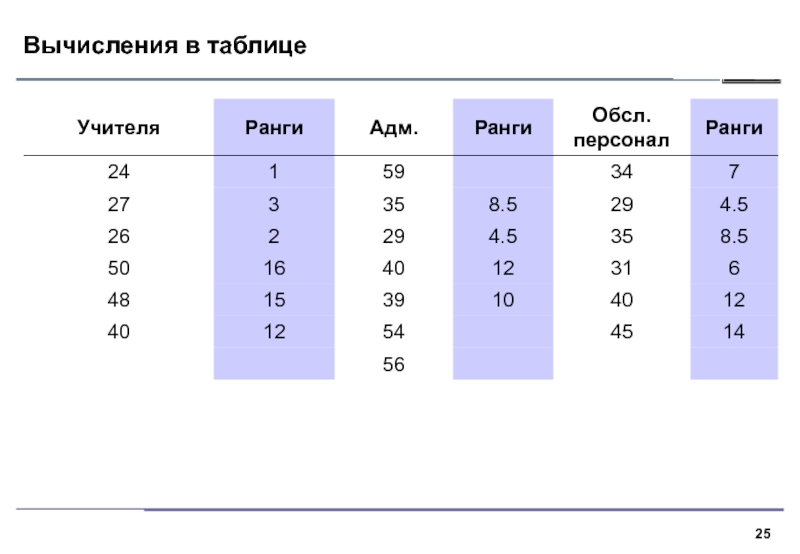
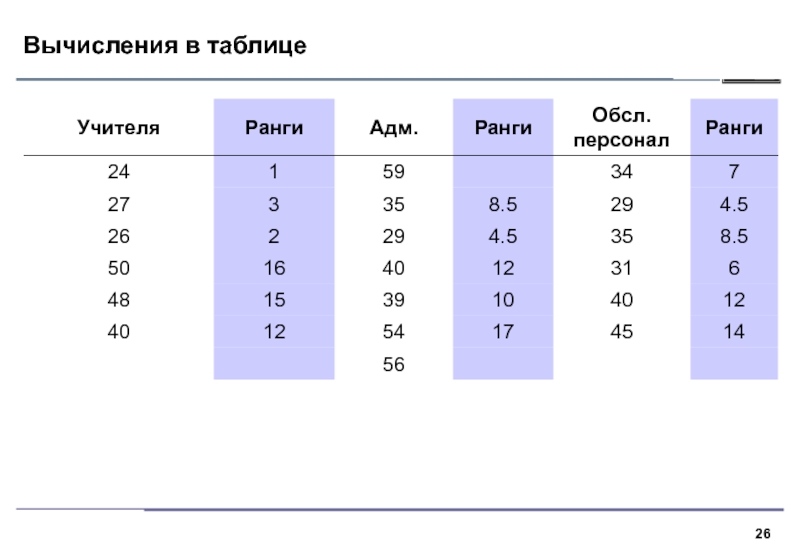
Слайд 12Суть критерия
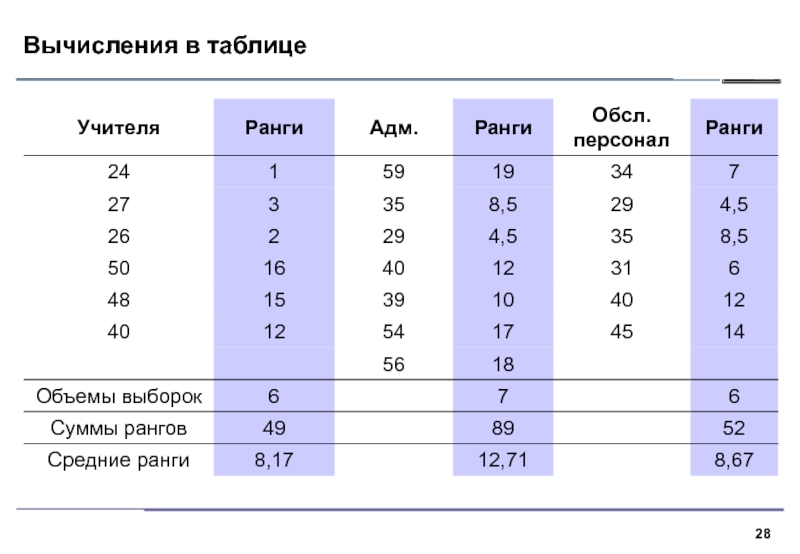
1. В критерии Краскела–Уоллиса все выборки объединяются и значения
ранжируются. Далее вычисляются средние ранги для каждой выборки и средний
ранг по всем данным.2. Если выборки взяты из различных совокупностей, средние ранги выборок будут сильно различаться, нулевая гипотеза однородности будет отвергнута.
Слайд 29Статистика
Формула статистики Краскела-Уоллиса:
где: – средние ранги выборок (i =
1,2,3,…,k)
– средний ранг по всем выборкам:
– объемы
выборок
Слайд 31Критическая область
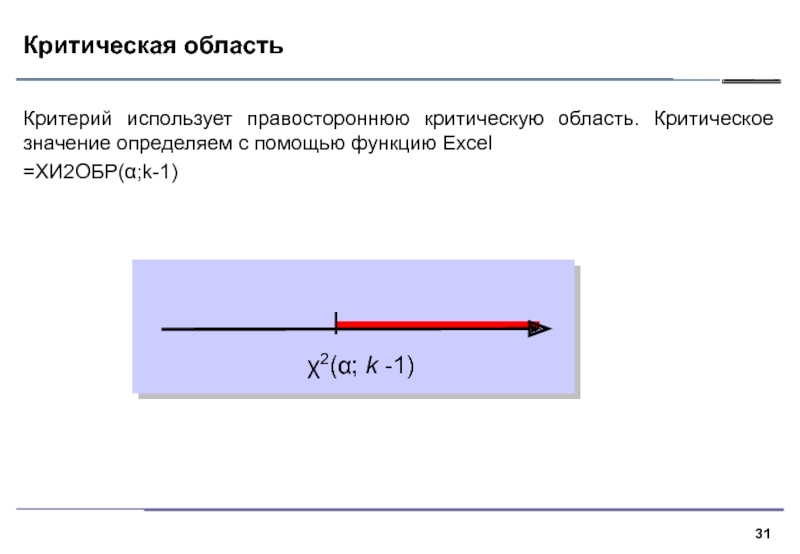
Критерий использует правостороннюю критическую область. Критическое значение определяем с
помощью функцию Excel
=ХИ2ОБР(α;k-1)
2(; k -1)
Слайд 32Находим границу критической области
Снова воспользуемся таблицами EXCEL для нахождения границы
критической области:
ХИ2ОБР (0,05; 2) = 5,991
Слайд 33Сравниваем и делаем вывод
Полученное значение статистики не попало в критическую
область:
Вывод. Мы не имеем оснований отклонить основную гипотезу. Значит, не
существует значимого различия в возрасте отдельных категорий персонала.5,991
2,602
Слайд 35Постановка задачи
Предположим, что для n объектов известны значения двух признаков.
- значения первого признака.
- значения второго признака.
Слайд 36Постановка задачи
Предположим, что для n объектов известны значения двух признаков.
- значения первого признака.
- значения второго признака.
Вычислим ранги каждого
наблюдения отдельно по каждой из выборок.- ранги объектов по первому признаку.
- ранги объектов по второму признаку.
Слайд 37Понятие рангового коэффициента корреляции
- ранги объектов по первому признаку.
-
ранги объектов по второму признаку.
Коэффициент ранговой корреляции Спирмена вычисляется по
той же формуле, что и обычный коэффициент корреляции, но вместо значений количественного признака используются ранги: 
Слайд 41пример.
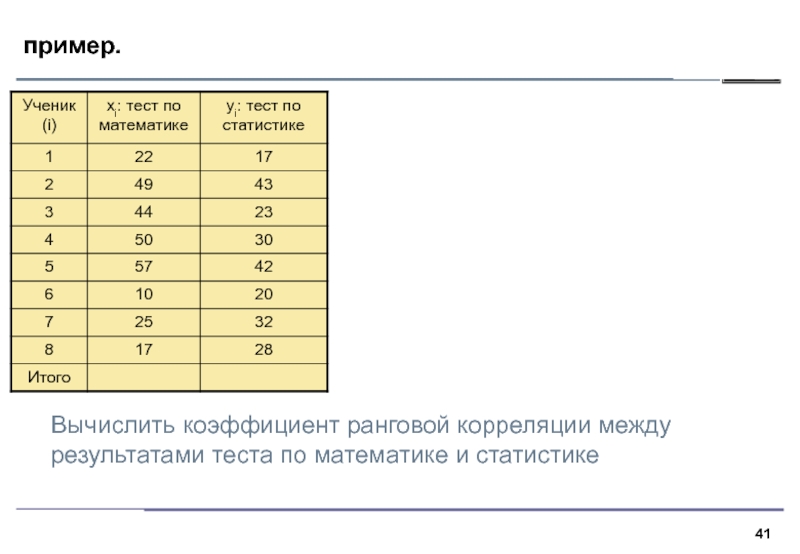
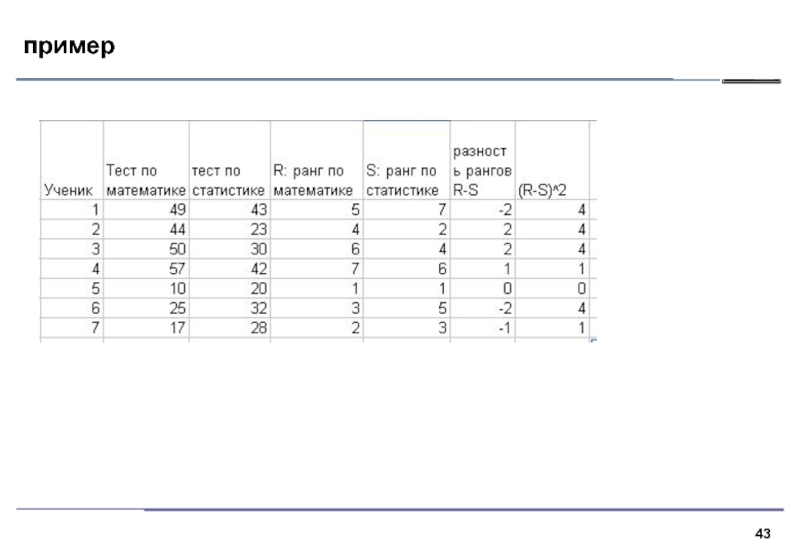
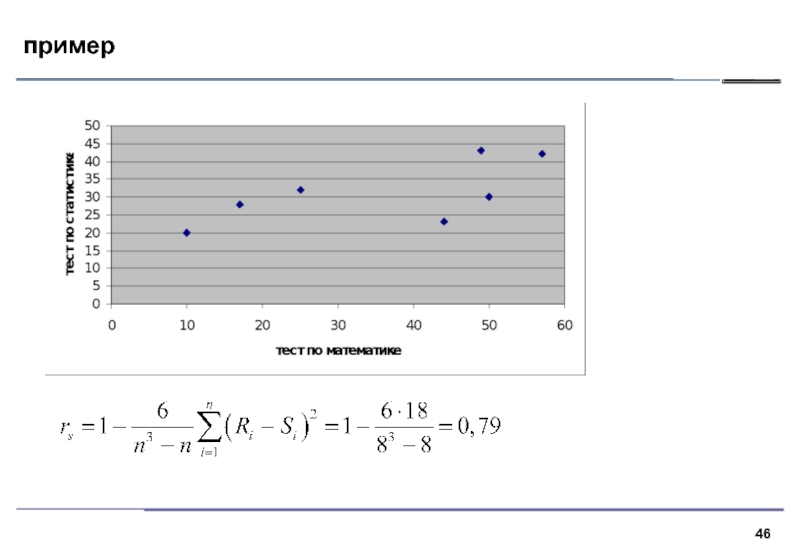
Вычислить коэффициент ранговой корреляции между
результатами теста по математике и
статистике
Слайд 47Проверка значимости рангового коэффициента корреляции
Обозначения:
Выборочный коэффициент корреляции Спирмена rs
Коэффициент корреляции
генеральной совокупности s
Требуется:
Проверить гипотезу о равенстве нулю коэффициента ранговой
корреляции генеральной совокупности на основании значения коэффициента ранговой корреляции выборки:H0 : s = 0 (признаки независимы)
H1 : s ≠ 0 (признаки зависимы)
Слайд 48Проверка значимости рангового коэффициента корреляции
Если исходные порядковые признаки независимы, то
статистика близка к 0.
Критическая область (двусторонняя) определяется с помощью
функции
Excel СТЬЮДРАСПОБРРассчитывается статистика
Слайд 51Проверка значимости рангового коэффициента корреляции
Проверим значимость
=СТЬЮДРАСПОБР(0,05;8-2)
2.45
Слайд 52Проверка значимости рангового коэффициента корреляции
Проверим значимость
=СТЬЮДРАСПОБР(0,05;8-2)
2.45
Принимаем гипотезу
H1 : s
≠ 0 (признаки зависимы)
Оценки по статистике и математике взаимосвязаны
Слайд 53Пример. Конкурс красоты
Два эксперта - мужчина и женщина, познакомились с
фотографиями десяти участниц конкурса красоты и выставили им оценки. Единицу
получила лучшая модель, оценку десять – наименее привлекательная.Проанализировать результаты оценок и на уровне значимости 0,05 сделать вывод, существует ли связь между мнениями мужчины и женщины по поводу привлекательности участниц.
Слайд 54Пример. Конкурс красоты
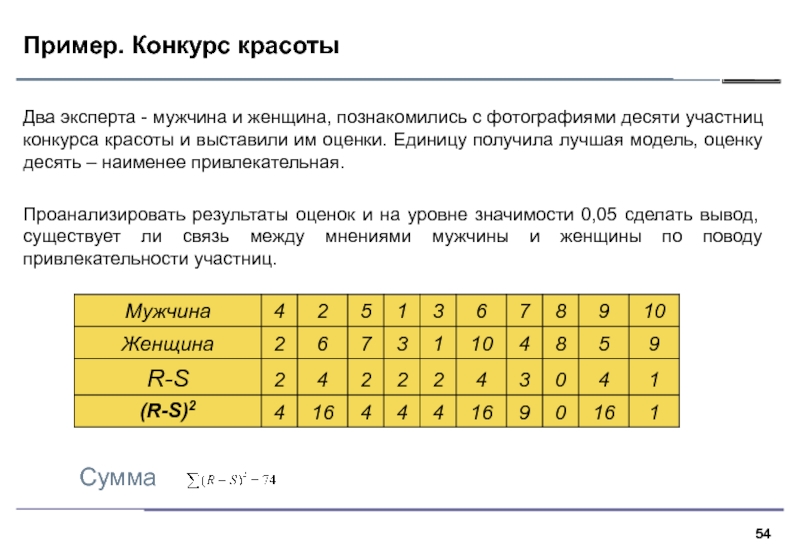
Два эксперта - мужчина и женщина, познакомились с
фотографиями десяти участниц конкурса красоты и выставили им оценки. Единицу
получила лучшая модель, оценку десять – наименее привлекательная.Проанализировать результаты оценок и на уровне значимости 0,05 сделать вывод, существует ли связь между мнениями мужчины и женщины по поводу привлекательности участниц.
Сумма
Слайд 57Решение.
Находим критическое значение
Получим 2,3
Критическая область задается неравенствами T
T>2,3
Статистика T=1,87 не попадает в критическую область
Вывод. Принимаем основную гипотезу.
Связь между мнениями мужчины и женщины по поводу привлекательности участниц отсутствует.=СТЬЮДРАСПОБР(0,05;10-2)
Слайд 58Решение в Excel
Критерий Краскелла-Уоллиса
Имеется ли разница в среднем возрасте
учителей, администрации и обслуживающего персонала школы? Взяты выборки из трех
генеральных совокупностей.
Слайд 61Решение в Excel
Критерий Краскелла-Уоллиса
Вычислим ранги с помощью функции РАНГ
Для
совпадающих наблюдений Excel
считает ранги некорректно!
Надо исправлять вручную
Слайд 64Решение в Excel
Критерий Краскелла-Уоллиса
Начиная с EXCEL 2010 появилась функция
РАНГ.СР, которая вычисляет ранги корректно
