Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оглавление
Содержание
- 1. Оглавление
- 2. Прямые линии общего положенияПрямые не параллельные и не перпендикулярные плоскостям проекцийZYOС2С1СD1DD2XXZYC2C1D2D1
- 3. Прямые линии
- 4. А1А2ZYXП1П3П2В1В2ZYВ1А2В2СЛЕДЫ ПРЯМОЙ ЛИНИИ СЛЕДЫ ПРЯМОЙ – ТОЧКИ
- 5. Относительное положение прямыхПрямые относительно друг друга могут располагаться:1. Параллельно2. Перпендикулярно3. Пересекаться4. Скрещиваться
- 6. Параллельные прямыеПроекции параллельных прямых параллельныXZYа2a1b2b1a II b
- 7. Перпендикулярные прямые Прямой угол, между прямыми линиями,
- 8. Пересекающиеся прямыеПересекающиеся прямые имеют одну общую точку.
- 9. Скрещивающиеся прямыеПрямые принадлежащие разным плоскостям, не параллельные
- 10. Ортогональные проекции плоскостиПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ
- 11. Способы задания плоскости
- 12. Графические способы задания плоскости
- 13. Графические способы задания плоскости XZYа2а1b2b1XZYa2a1b2b13. Параллельные прямые4. Пересекающиеся прямыеК1К2
- 14. Графические способы задания плоскостиXZYА2А1В1C2C1В25. Плоская фигура
- 15. Графические способы задания плоскостиYZXaП1aП3aП2aXaYaZ6. Следы плоскости –
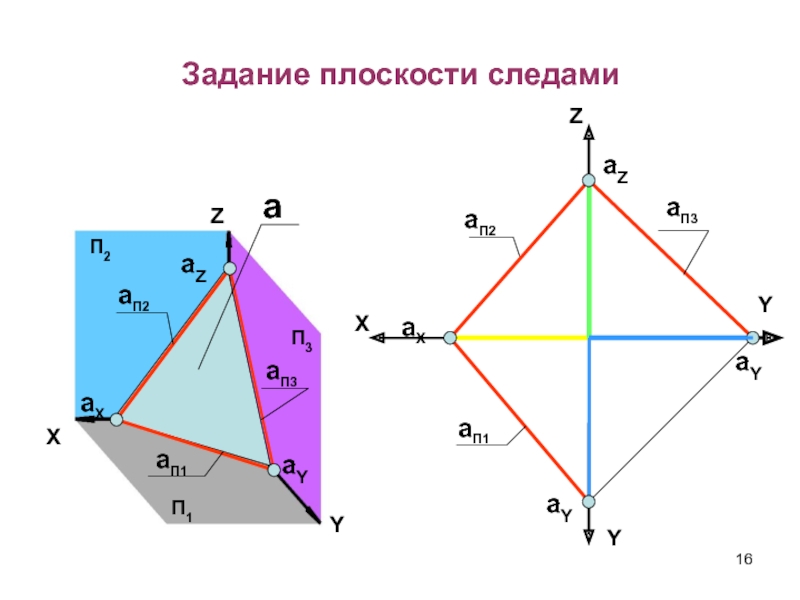
- 16. Задание плоскости следамиZXYYaП2aП1aП3aXaYaZZXaП1aП3aП2aXaYaZaaYYП2П1П3
- 17. Относительное положение плоскостей относительно плоскостей проекций1. Относительно
- 18. Плоскости уровняГоризонтальная плоскость уровня параллельна горизонтальной плоскости проекций.ZXYYaП2aП3azYZXaП3aП2azaП2П3П1Плоскость aII П1А1В1С1А2В2С2А3В3=C3
- 19. ZXYYbП1bП3byYZXbП1bП3bybyФронтальная плоскость уровня параллельна фронтальной плоскости проекций.А1В1С1С2В2А2bП3П2П1В3А3=С3Плоскость Il П2
- 20. ZXYYgП2gп1gxYZXgП1gП2gxgПрофильная плоскость уровня параллельна профильной плоскости проекций.П2П3П1ПЛОСКОСТЬ II П3А3В3С3А2В2С2А1=С1 В1
- 21. Проецирующие плоскостиГоризонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций.XYYaП2aП3ZXaП1aП2axaxZaП1aП3aYayyayayА1В1С1А2В2С2П2П3П1А3B3C3Плоскость a П1
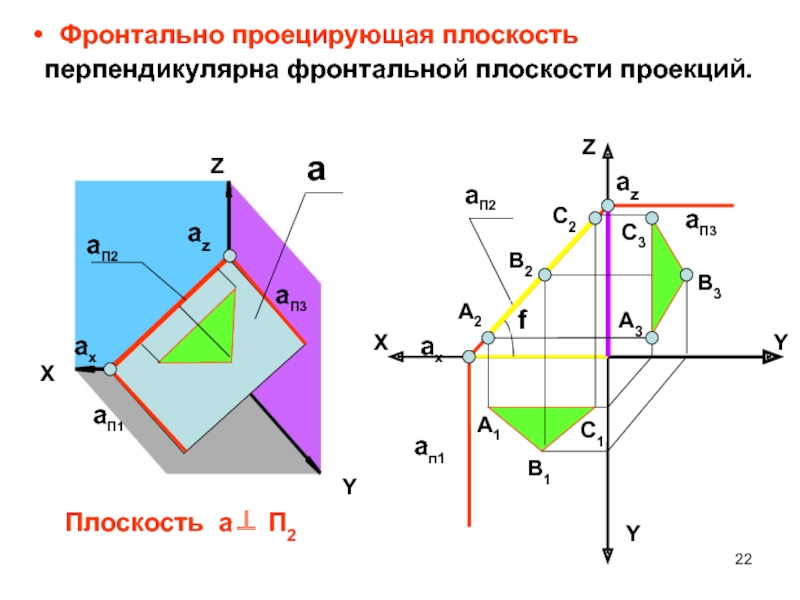
- 22. Фронтально проецирующая плоскость перпендикулярна фронтальной плоскости проекций.ZXYYaП2aп1axYZXaП2azaaП3aП1aП3azaxА2В2С2А1В1С1fС3А3В3Плоскость a П2
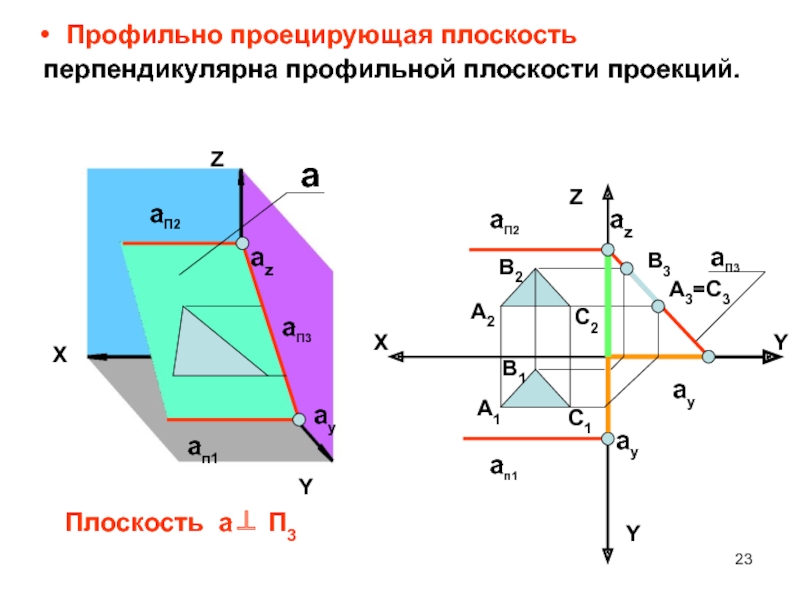
- 23. Профильно проецирующая плоскость перпендикулярна профильной плоскости проекций.ZXYYaП2aп1YZXaп1aП2aП3aaП3azayazayayА3=C3В3А2C2В2А1C1В1Плоскость a П3
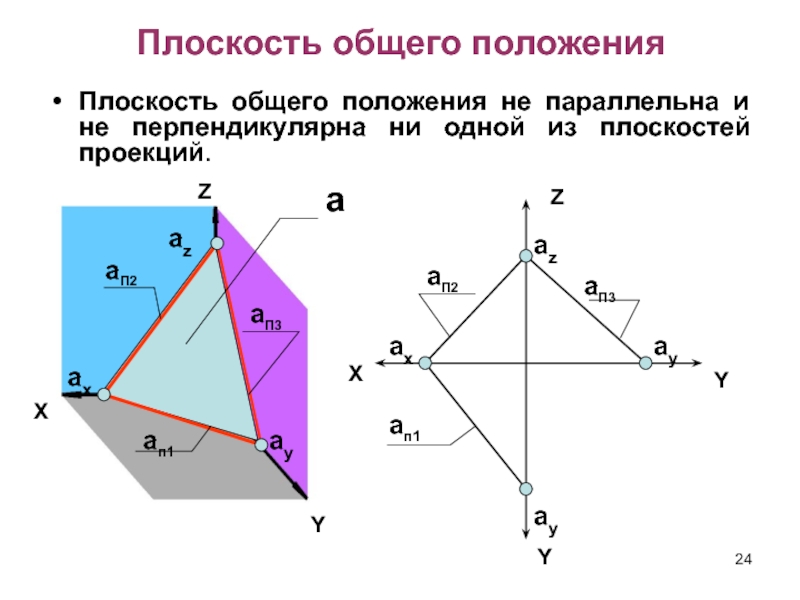
- 24. Плоскость общего положенияПлоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.YZXaп1aП3aП2axayazaXYYZaxayayazaп1aП2aП3
- 25. Плоскости
- 26. Принадлежность точки и прямой плоскостиТочка принадлежит плоскости,
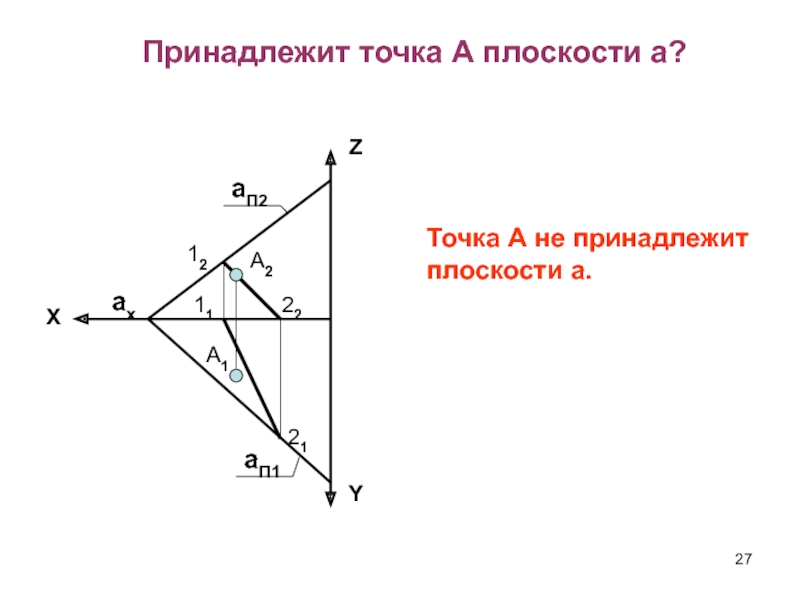
- 27. Принадлежит точка А плоскости a? А2А1aП2aП1axYZXТочка А не принадлежит плоскости a.12222111
- 28. Особые линии плоскостиЛИНИИ УРОВНЯ ПЛОСКОСТИ – линии
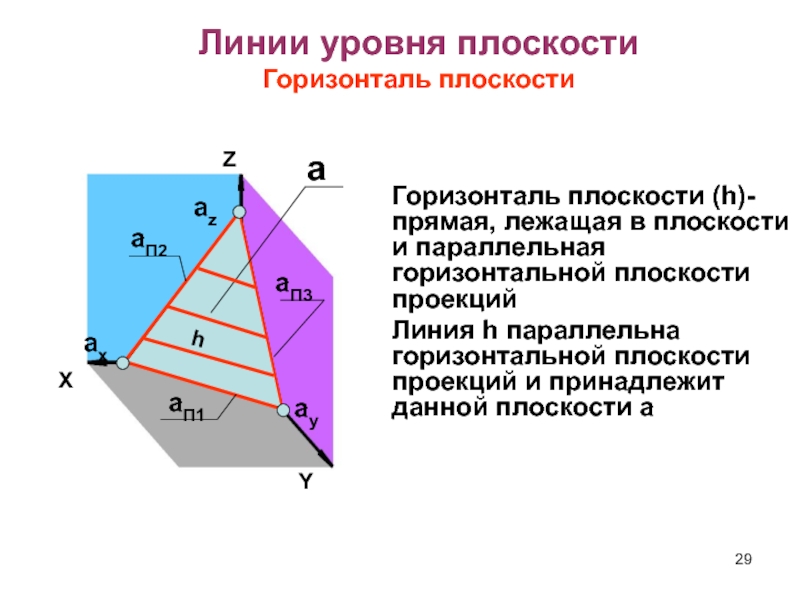
- 29. ZXaП1aП3aП2axayazaЛинии уровня плоскостиГоризонталь плоскостиYГоризонталь плоскости (h)- прямая,
- 30. Линия h параллельна горизонтальной плоскости проекций и принадлежит данной плоскости aЛинии уровня плоскостиГоризонталь плоскостиaП2aП1YZXaxА2А1h2h1F2F1ayaz
- 31. Линия h параллельна горизонтальной плоскости
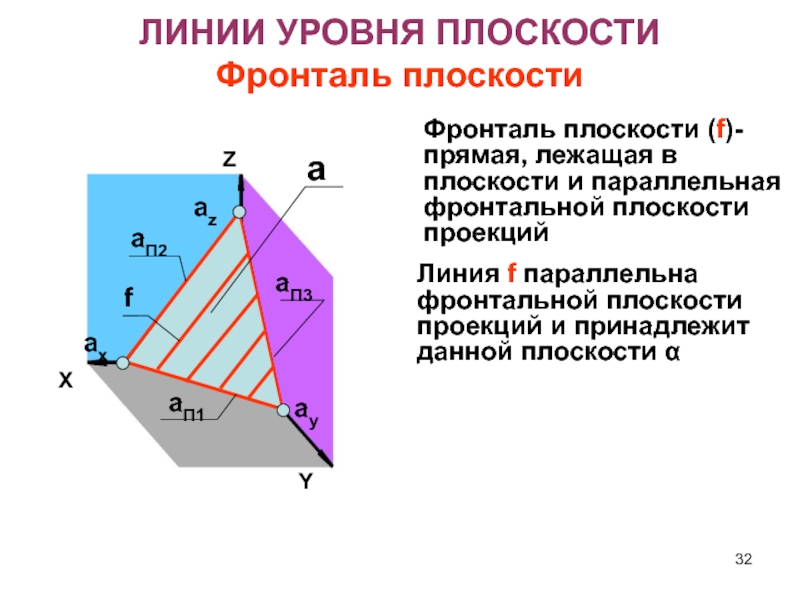
- 32. ЛИНИИ УРОВНЯ ПЛОСКОСТИ Фронталь плоскости ZXaП1aП3aП2axayazaYФронталь плоскости
- 33. Линия f
- 34. А2F2В2С2В1С1А1F1ЛИНИИ УРОВНЯ ПЛОСКОСТИФронталь плоскости
- 35. ЛИНИИ УРОВНЯ ПЛОСКОСТИПрофильная прямая плоскостиaП2aП1YZaxС2С1р3XaП3С3р2р1Линия р параллельна профильной плоскости проекций и принадлежит данной плоскости aYazayayL3L1L2
- 36. ZXaП1aП3aП2axayazaЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИК ПЛОСКОСТЯМ ПРОЕКЦИЙЛиния наибольшего
- 37. Линия наибольшего наклона плоскости α к горизонтальной
- 38. Линия наибольшего наклона плоскости ΔАВС к горизонтальной
- 39. ZXaП1aП3aП2axayazaЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИЛиния наибольшего наклона плоскости
- 40. Линия наибольшего наклона плоскости α к фронтальной
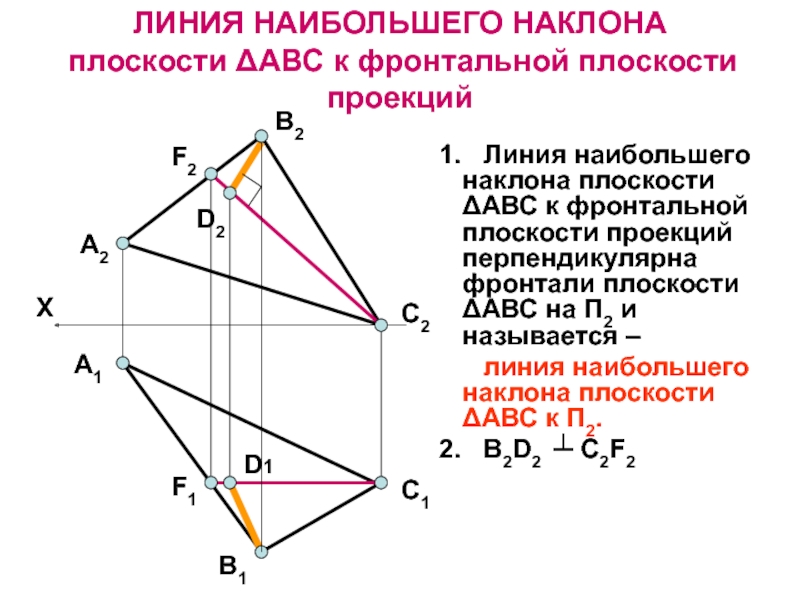
- 41. А2F2В2А1F1ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА плоскости ΔАВС к фронтальной
- 42. Пример.Построить проекции равнобедренного треугольника ΔАВС принадлежащего
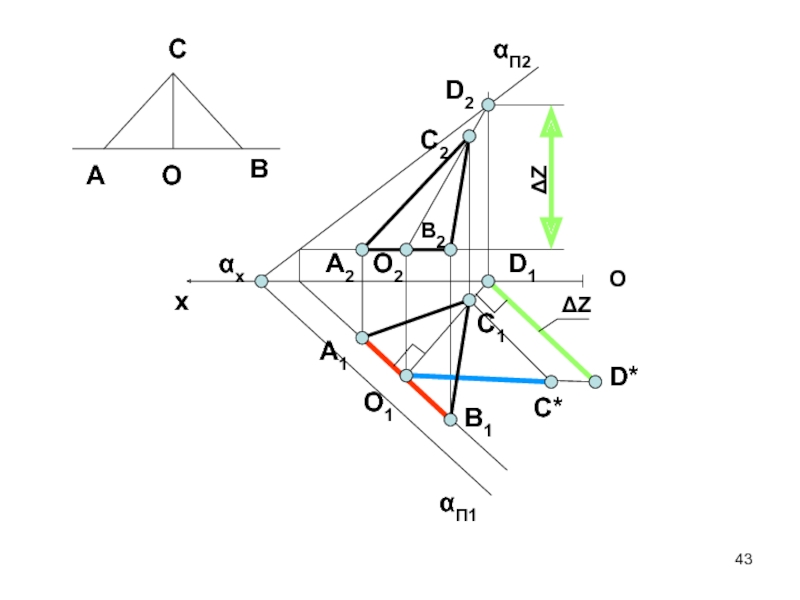
- 43. D2D1D*αxC2B2A2B1A1C1C*O1O2ΔZΔZxαП1αП2ОAВСО
- 44. НОРМАЛЬ ПЛОСКОСТИ Нормаль плоскости n – линия перпендикулярная заданной плоскости.ZXaП1aП3aП2axayazYan
- 45. Проекции нормали перпендикулярны проекциям линий уровня плоскости
- 46. НОРМАЛЬ ПЛОСКОСТИ Нормаль плоскости n –
- 47. Скачать презентанцию
Слайды и текст этой презентации
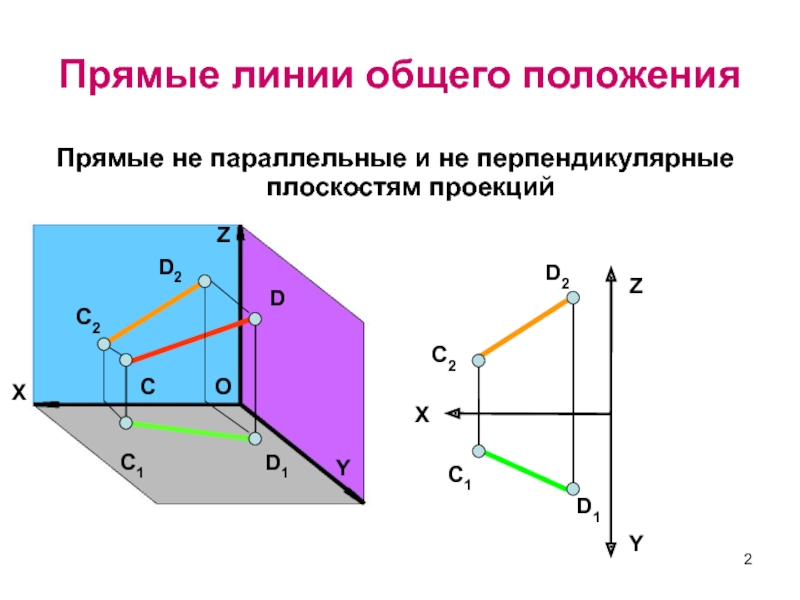
Слайд 2Прямые линии общего положения
Прямые не параллельные и не перпендикулярные плоскостям
проекций
Слайд 4А1
А2
Z
Y
X
П1
П3
П2
В1
В2
Z
Y
В1
А2
В2
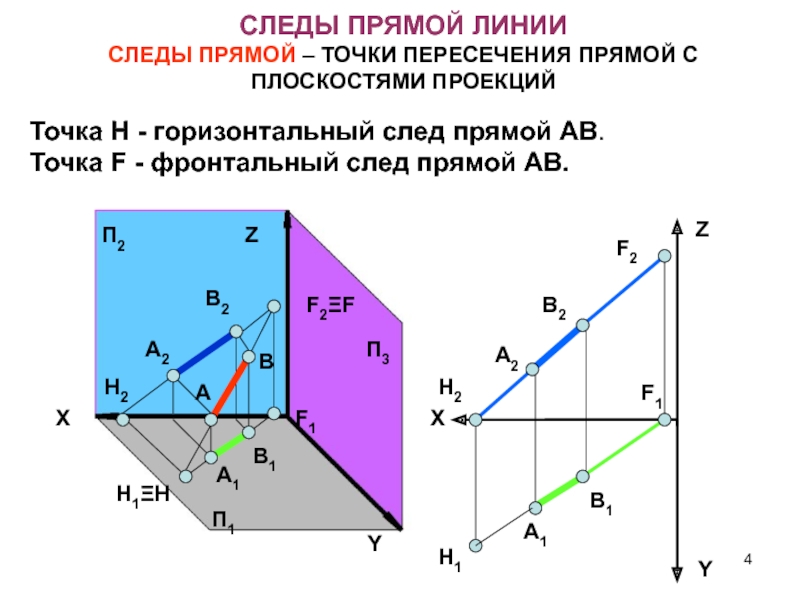
СЛЕДЫ ПРЯМОЙ ЛИНИИ
СЛЕДЫ ПРЯМОЙ – ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЯМИ
ПРОЕКЦИЙ
Точка H - горизонтальный след прямой АВ.
Точка F - фронтальный
след прямой АВ.А1
X
А
B
H1ΞH
F2ΞF
H2
F1
F2
F1
H2
H1
Слайд 5Относительное положение прямых
Прямые относительно друг друга могут располагаться:
1. Параллельно
2. Перпендикулярно
3.
Пересекаться
4. Скрещиваться
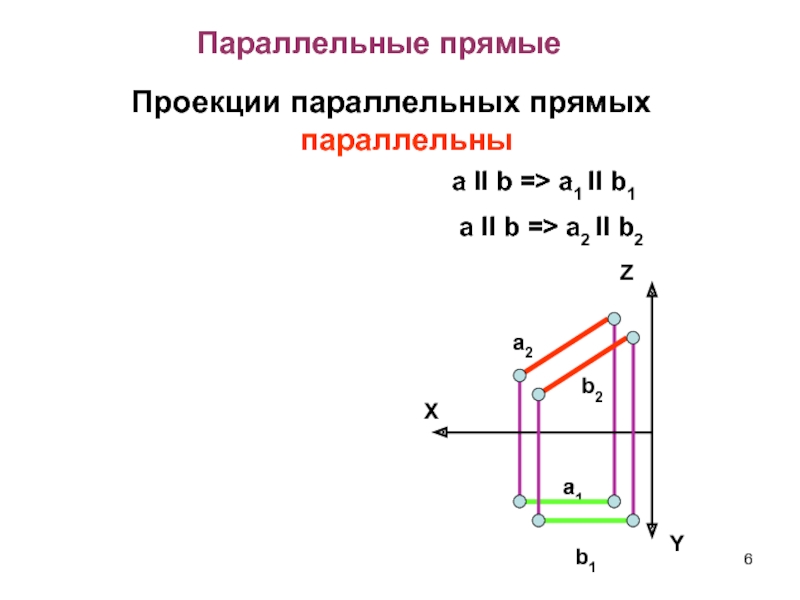
Слайд 6Параллельные прямые
Проекции параллельных прямых параллельны
X
Z
Y
а2
a1
b2
b1
a II b => a1 II
b1
a II b => a2 II b2
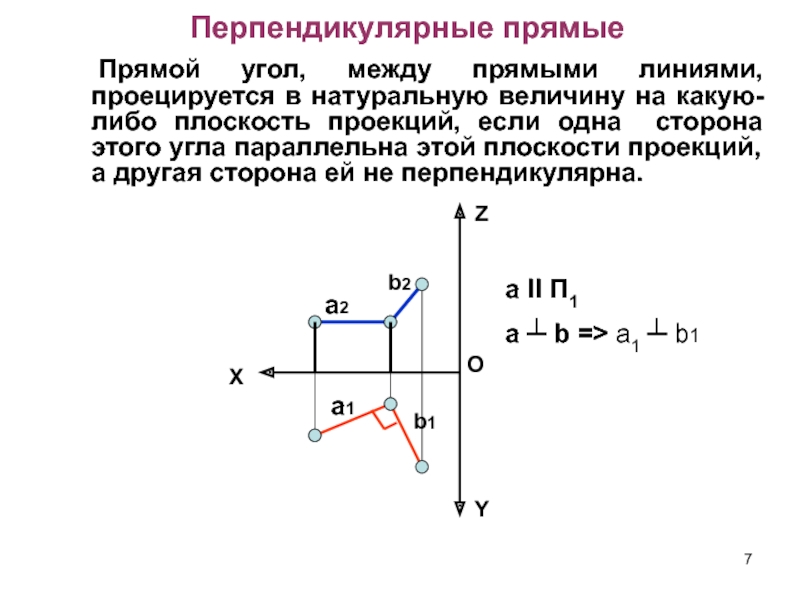
Слайд 7Перпендикулярные прямые
Прямой угол, между прямыми линиями, проецируется в натуральную
величину на какую-либо плоскость проекций, если одна сторона этого угла
параллельна этой плоскости проекций, а другая сторона ей не перпендикулярна.X
Y
Z
a2
b2
a1
b1
O
a II П1
a ┴ b => a1 ┴ b1
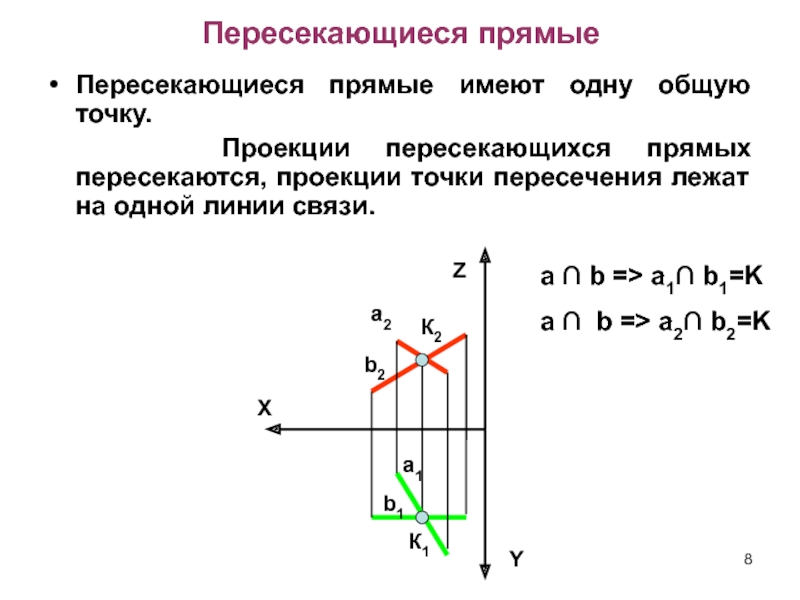
Слайд 8Пересекающиеся прямые
Пересекающиеся прямые имеют одну общую точку.
Проекции
пересекающихся прямых пересекаются, проекции точки пересечения лежат на одной линии
связи.X
Z
Y
a2
К1
b2
b1
a1
К2
a ∩ b => a1∩ b1=K
a ∩ b => a2∩ b2=K
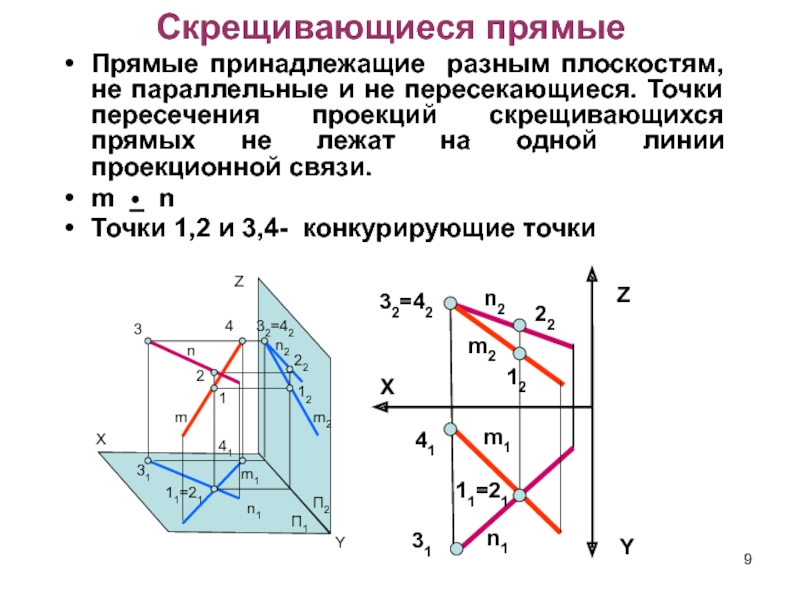
Слайд 9Скрещивающиеся прямые
Прямые принадлежащие разным плоскостям, не параллельные и не пересекающиеся.
Точки пересечения проекций скрещивающихся прямых не лежат на одной линии
проекционной связи.m _ n
Точки 1,2 и 3,4- конкурирующие точки
m1
n1
m2
n2
n
П1
m
П2
11=21
12
22
2
1
X
Z
m1
n2
n1
m2
11=21
12
22
Y
X
Z
Y
3
4
32=42
31
41
32=42
31
41
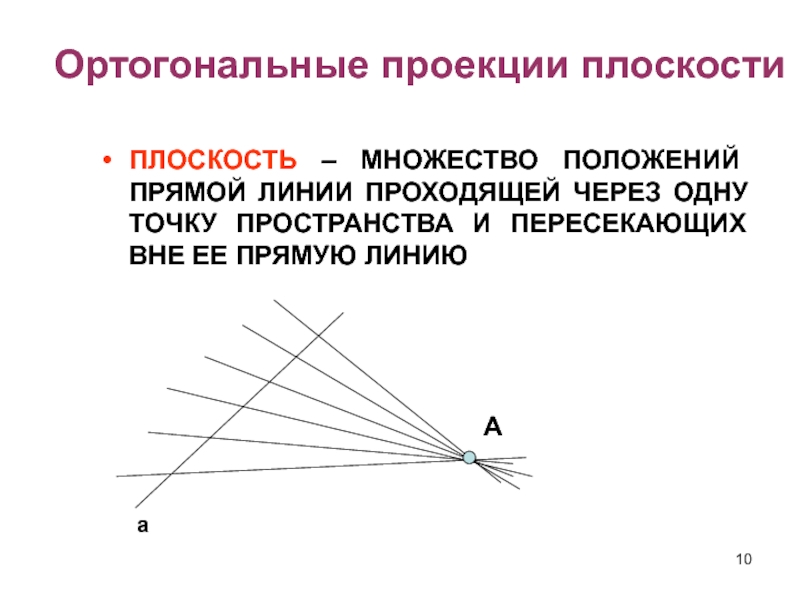
Слайд 10Ортогональные проекции плоскости
ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ
ОДНУ ТОЧКУ ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ ЛИНИЮ
A
a
Слайд 11Способы задания плоскости
1. Аналитический способ
Аx + By
+ Cz + D = 0
2. Графические способы
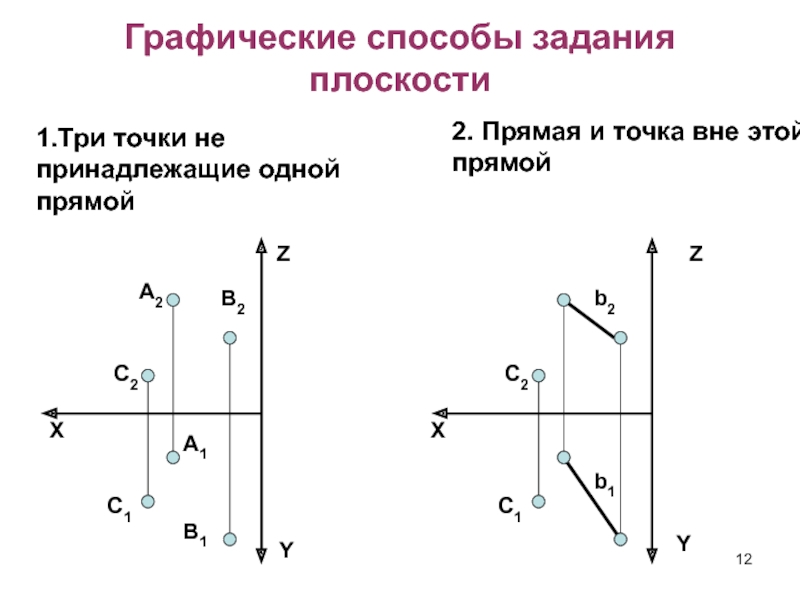
Слайд 12 Графические способы задания плоскости
X
Z
Y
А2
А1
В1
C2
C1
В2
X
Y
b1
C2
C1
b2
1.Три точки не принадлежащие одной прямой
2. Прямая и точка вне
этой прямойZ
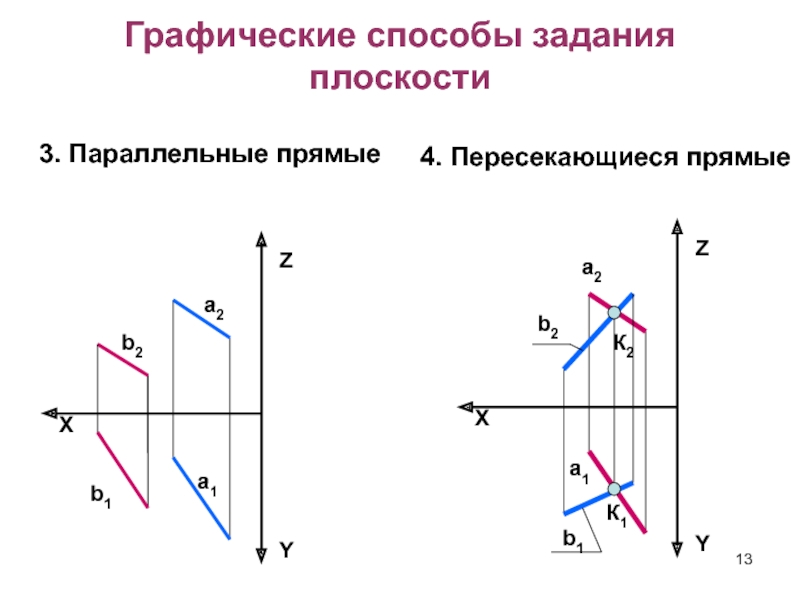
Слайд 13Графические способы задания плоскости
X
Z
Y
а2
а1
b2
b1
X
Z
Y
a2
a1
b2
b1
3. Параллельные прямые
4. Пересекающиеся прямые
К1
К2
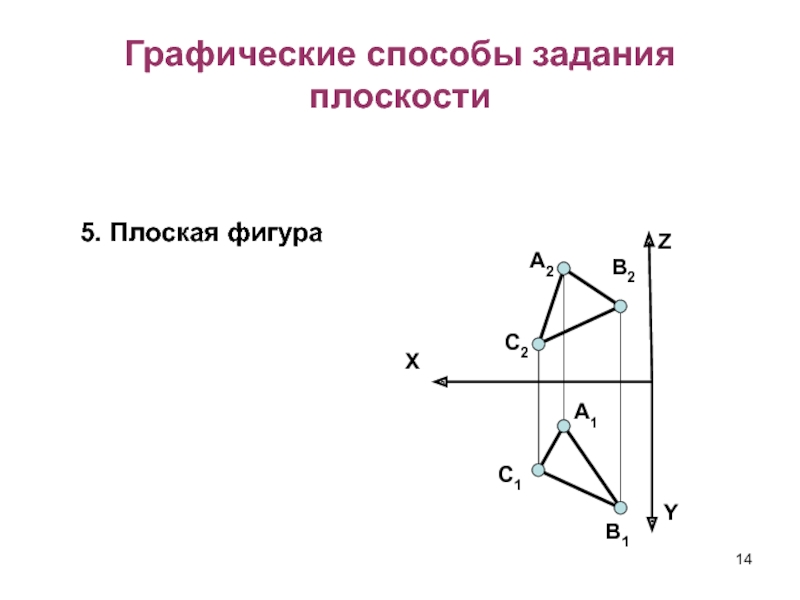
Слайд 15Графические способы задания плоскости
Y
Z
X
aП1
aП3
aП2
aX
aY
aZ
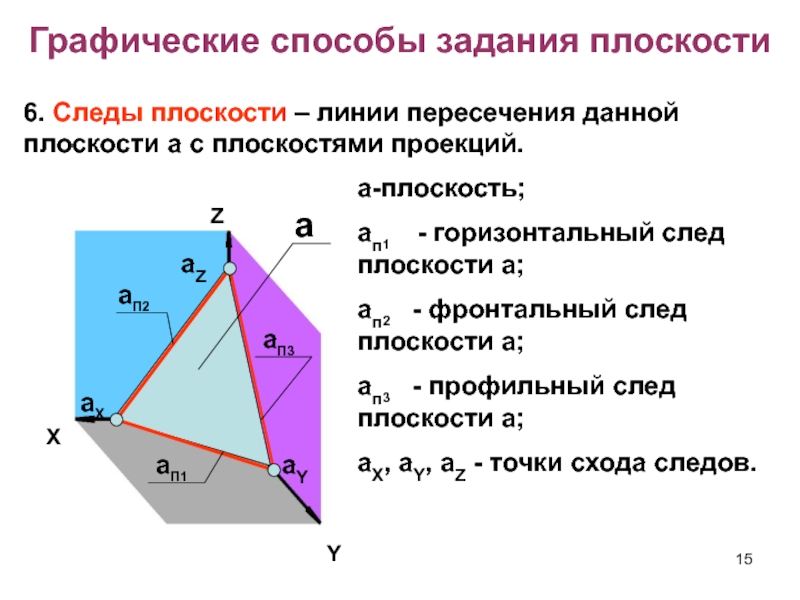
6. Следы плоскости – линии пересечения данной
плоскости a с плоскостями проекций.
a
a-плоскость;
aп1 - горизонтальный след плоскости
a; aп2 - фронтальный след плоскости a;
aп3 - профильный след плоскости a;
aX, aY, aZ - точки схода следов.
Слайд 17Относительное положение плоскостей
относительно плоскостей проекций
1. Относительно плоскостей проекций плоскости разделяют:
• плоскости частного положения
• плоскости общего положения
2. Плоскости частного положения разделяют:
плоскости параллельные плоскостям проекций – плоскости уровня
плоскости перпендикулярные плоскостям проекций – плоскости проецирующие
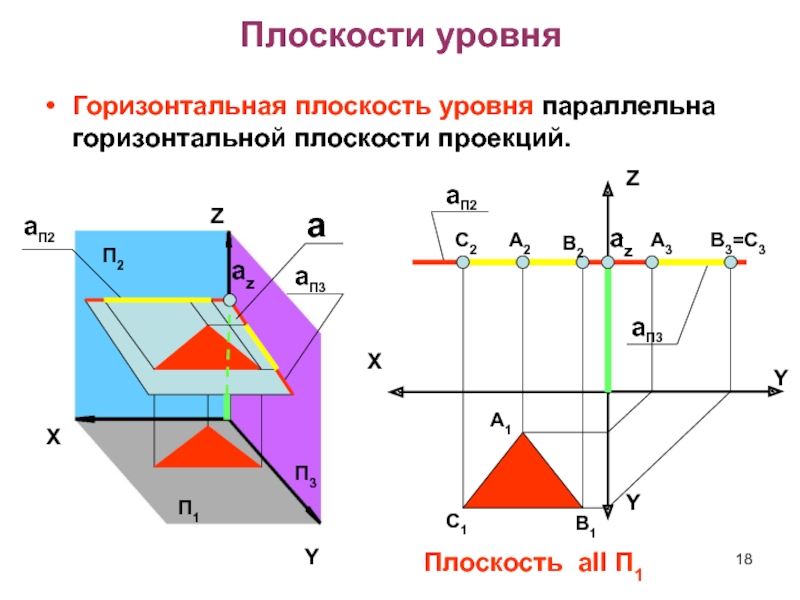
Слайд 18Плоскости уровня
Горизонтальная плоскость уровня параллельна горизонтальной плоскости проекций.
Z
X
Y
Y
aП2
aП3
az
Y
Z
X
aП3
aП2
az
a
П2
П3
П1
Плоскость aII П1
А1
В1
С1
А2
В2
С2
А3
В3=C3
Слайд 19Z
X
Y
Y
bП1
bП3
by
Y
Z
X
bП1
bП3
by
by
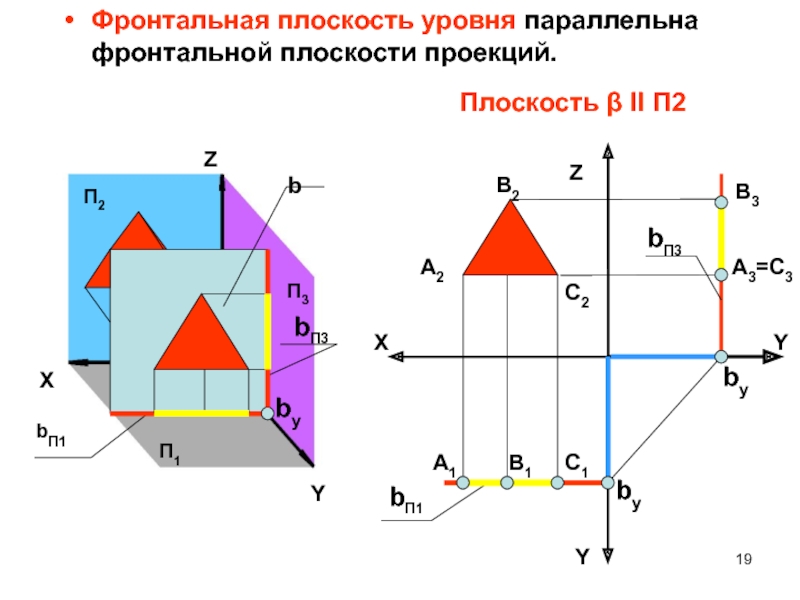
Фронтальная плоскость уровня параллельна фронтальной плоскости проекций.
А1
В1
С1
С2
В2
А2
b
П3
П2
П1
В3
А3=С3
Плоскость Il П2
Слайд 20Z
X
Y
Y
gП2
gп1
gx
Y
Z
X
gП1
gП2
gx
g
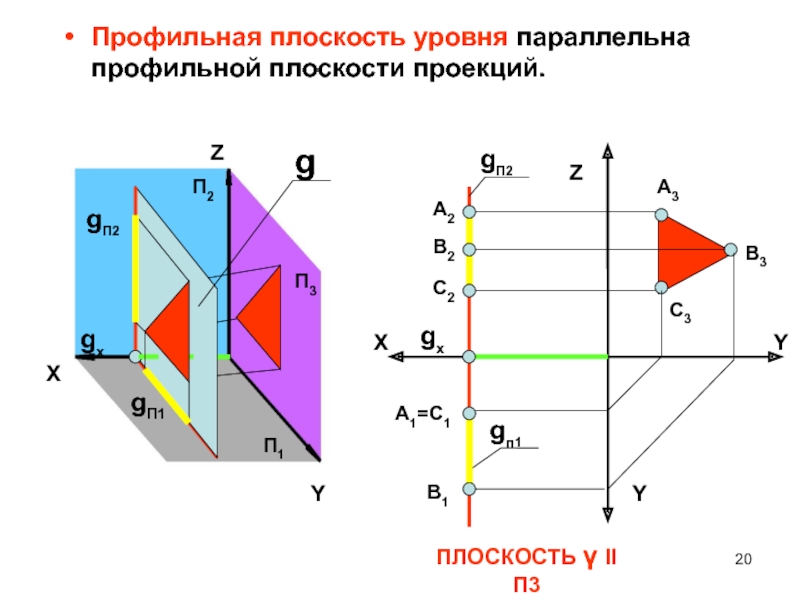
Профильная плоскость уровня параллельна профильной плоскости проекций.
П2
П3
П1
ПЛОСКОСТЬ II П3
А3
В3
С3
А2
В2
С2
А1=С1
В1
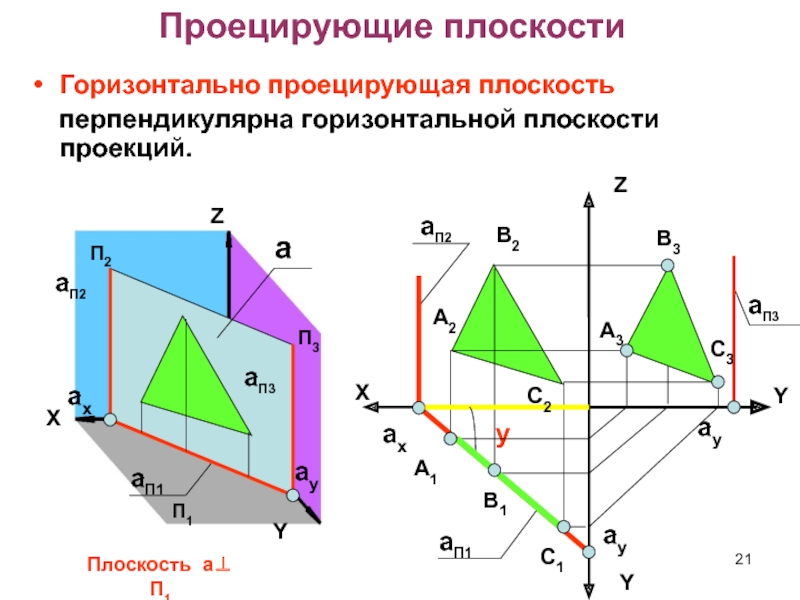
Слайд 21Проецирующие плоскости
Горизонтально проецирующая плоскость
перпендикулярна горизонтальной плоскости проекций.
X
Y
Y
aП2
aП3
Z
X
aП1
aП2
ax
ax
Z
aП1
aП3
a
Y
ay
y
ay
ay
А1
В1
С1
А2
В2
С2
П2
П3
П1
А3
B3
C3
Плоскость
a П1
Слайд 22Фронтально проецирующая плоскость
перпендикулярна фронтальной плоскости проекций.
Z
X
Y
Y
aП2
aп1
ax
Y
Z
X
aП2
az
a
aП3
aП1
aП3
az
ax
А2
В2
С2
А1
В1
С1
f
С3
А3
В3
Плоскость a П2
Слайд 23Профильно проецирующая плоскость
перпендикулярна профильной плоскости проекций.
Z
X
Y
Y
aП2
aп1
Y
Z
X
aп1
aП2
aП3
a
aП3
az
ay
az
ay
ay
А3=C3
В3
А2
C2
В2
А1
C1
В1
Плоскость a П3
Слайд 24Плоскость общего положения
Плоскость общего положения не параллельна и не перпендикулярна
ни одной из плоскостей проекций.
Y
Z
X
aп1
aП3
aП2
ax
ay
az
a
X
Y
Y
Z
ax
ay
ay
az
aп1
aП2
aП3
Слайд 26Принадлежность точки и прямой
плоскости
Точка принадлежит плоскости, если она принадлежит
прямой в этой плоскости
Прямая принадлежит плоскости если она проходит:
а) через
две точки этой плоскостиб) через точку плоскости и параллельна какой-либо прямой этой плоскости
Слайд 28Особые линии плоскости
ЛИНИИ УРОВНЯ ПЛОСКОСТИ – линии параллельные плоскостям проекций
и принадлежащие данной плоскости;
ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ – определяют угол
наклона данной плоскости к одной из плоскостей проекций. ЛНН перпендикулярны линиям уровня:
горизонтали на плоскости П1;
фронтали на плоскости П2.
Слайд 29Z
X
aП1
aП3
aП2
ax
ay
az
a
Линии уровня плоскости
Горизонталь плоскости
Y
Горизонталь плоскости (h)- прямая, лежащая в плоскости
и параллельная горизонтальной плоскости проекций
Линия h параллельна горизонтальной плоскости
проекций и принадлежит данной плоскости ah
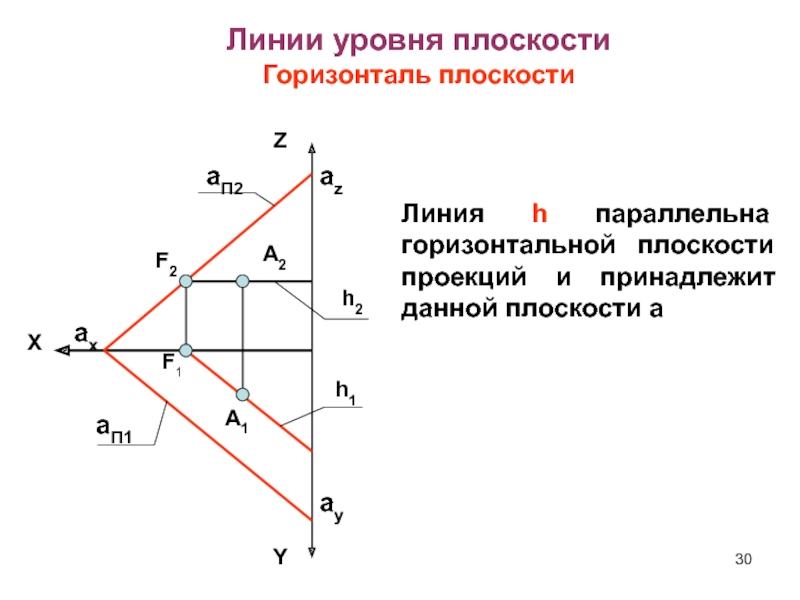
Слайд 30Линия h параллельна горизонтальной плоскости проекций и принадлежит данной плоскости
a
Линии уровня плоскости
Горизонталь плоскости
aП2
aП1
Y
Z
X
ax
А2
А1
h2
h1
F2
F1
ay
az
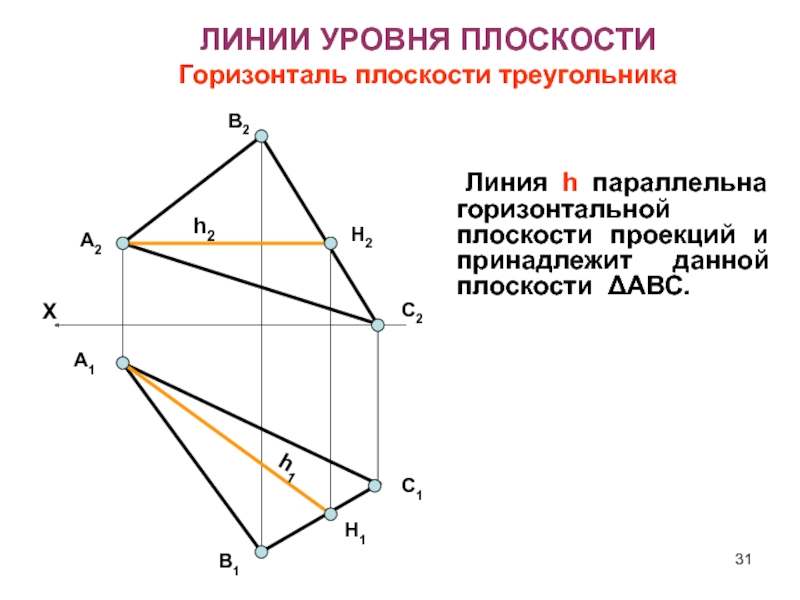
Слайд 31 Линия h параллельна горизонтальной плоскости проекций и принадлежит
данной плоскости ΔАВС.
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Горизонталь плоскости треугольника
А2
В2
С2
H2
В1
С1
А1
H1
X
h2
h1
Слайд 32ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Фронталь плоскости
Z
X
aП1
aП3
aП2
ax
ay
az
a
Y
Фронталь плоскости (f)- прямая, лежащая в плоскости
и параллельная фронтальной плоскости проекций
f
Линия f параллельна фронтальной плоскости
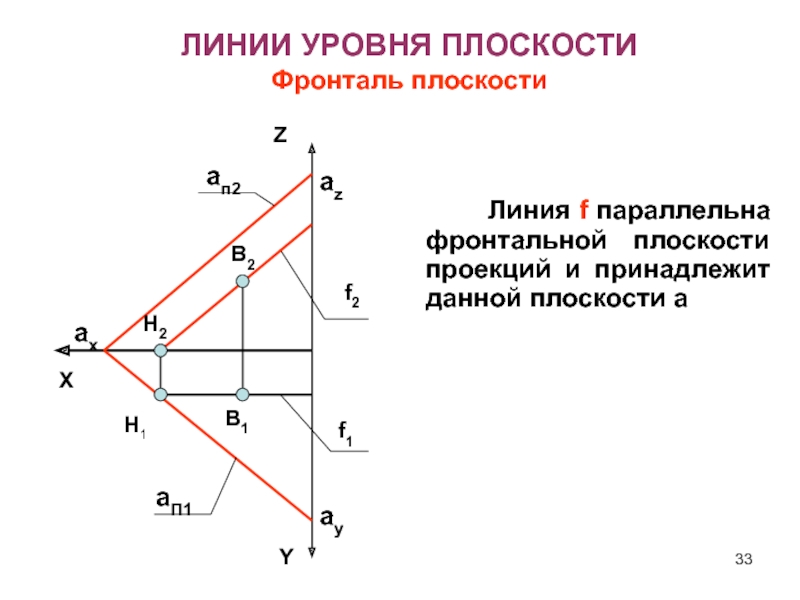
проекций и принадлежит данной плоскости Слайд 33 Линия f параллельна фронтальной плоскости
проекций и принадлежит данной плоскости a
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Фронталь плоскости
aп2
aП1
Y
Z
ax
В2
В1
f2
f1
H2
H1
X
az
ay
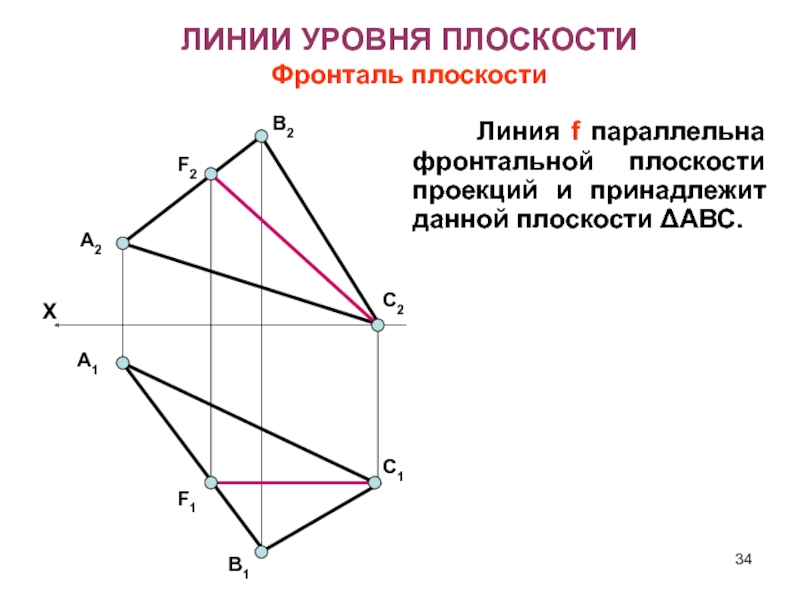
Слайд 34А2
F2
В2
С2
В1
С1
А1
F1
ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Фронталь плоскости
Линия f
параллельна фронтальной плоскости проекций и принадлежит данной плоскости ΔАВС.
X
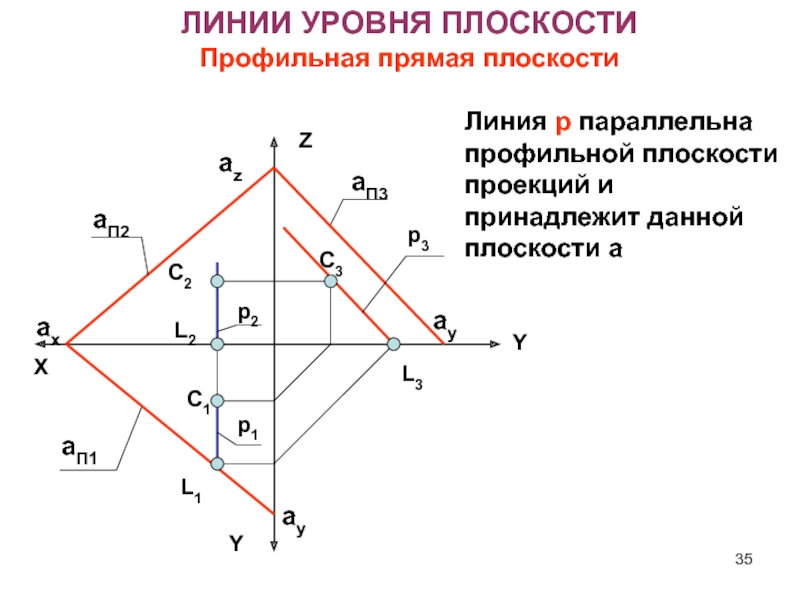
Слайд 35ЛИНИИ УРОВНЯ ПЛОСКОСТИ
Профильная прямая плоскости
aП2
aП1
Y
Z
ax
С2
С1
р3
X
aП3
С3
р2
р1
Линия р параллельна профильной плоскости проекций
и принадлежит данной плоскости a
Y
az
ay
ay
L3
L1
L2
Слайд 36Z
X
aП1
aП3
aП2
ax
ay
az
a
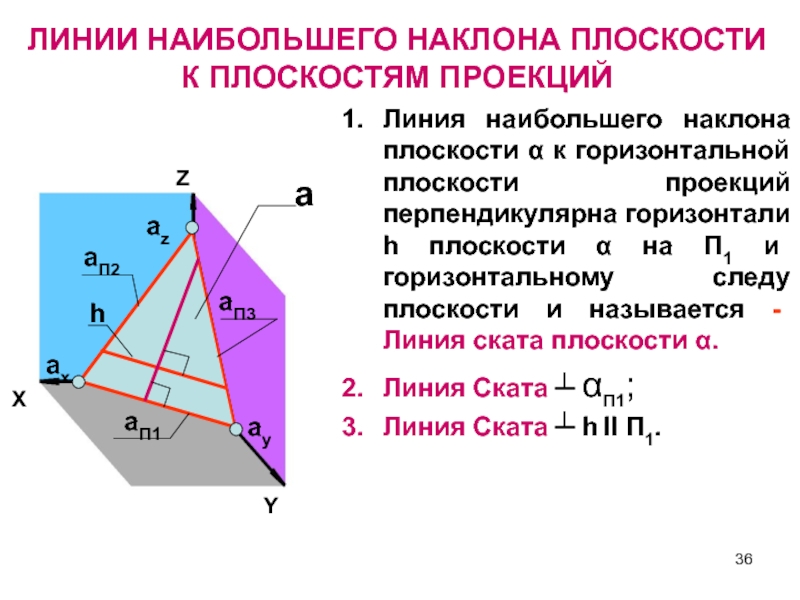
ЛИНИИ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
К ПЛОСКОСТЯМ ПРОЕКЦИЙ
Линия наибольшего наклона плоскости α
к горизонтальной плоскости проекций перпендикулярна горизонтали h плоскости α на
П1 и горизонтальному следу плоскости и называется - Линия ската плоскости α.Линия Ската ┴ αП1;
Линия Ската ┴ h II П1.
h
Y
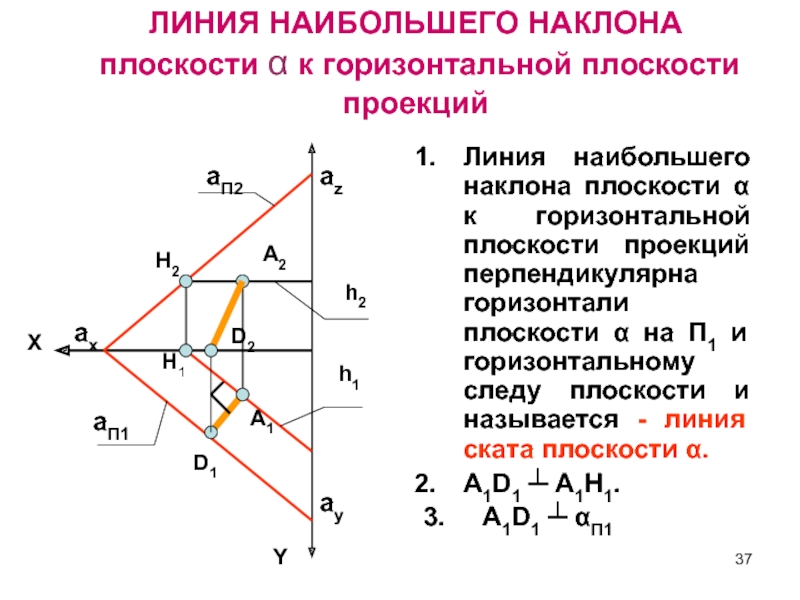
Слайд 37Линия наибольшего наклона плоскости α к горизонтальной плоскости проекций перпендикулярна
горизонтали плоскости α на П1 и горизонтальному следу плоскости и
называется - линия ската плоскости α.А1D1 ┴ А1H1.
3. А1D1 ┴ αП1
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости α к горизонтальной плоскости проекций
aП2
aП1
Y
X
ax
А2
А1
h2
h1
H2
H1
ay
az
D1
D2
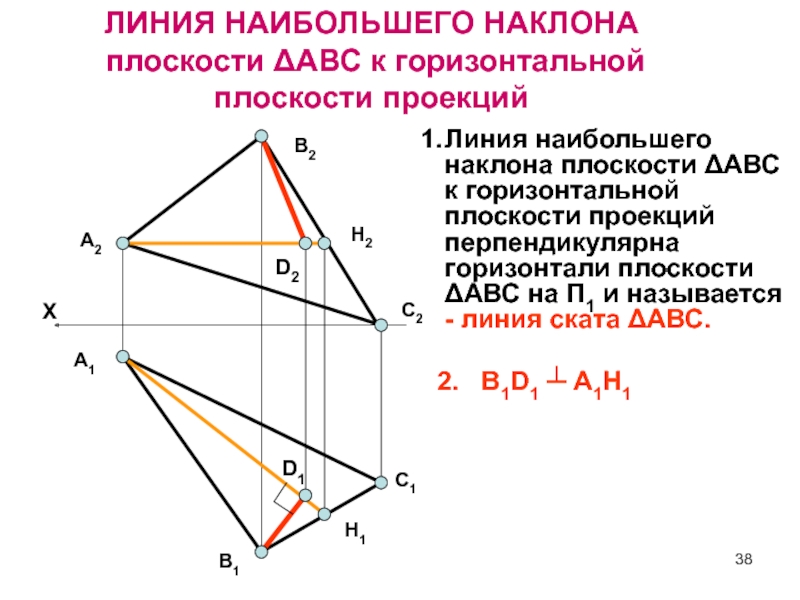
Слайд 38Линия наибольшего наклона плоскости ΔАВС к горизонтальной плоскости проекций перпендикулярна
горизонтали плоскости ΔАВС на П1 и называется - линия ската
ΔАВС.2. В1D1 ┴ А1H1
А2
В2
С2
H2
В1
С1
А1
H1
X
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости ΔАВС к горизонтальной плоскости проекций
D1
D2
Слайд 39Z
X
aП1
aП3
aП2
ax
ay
az
a
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ
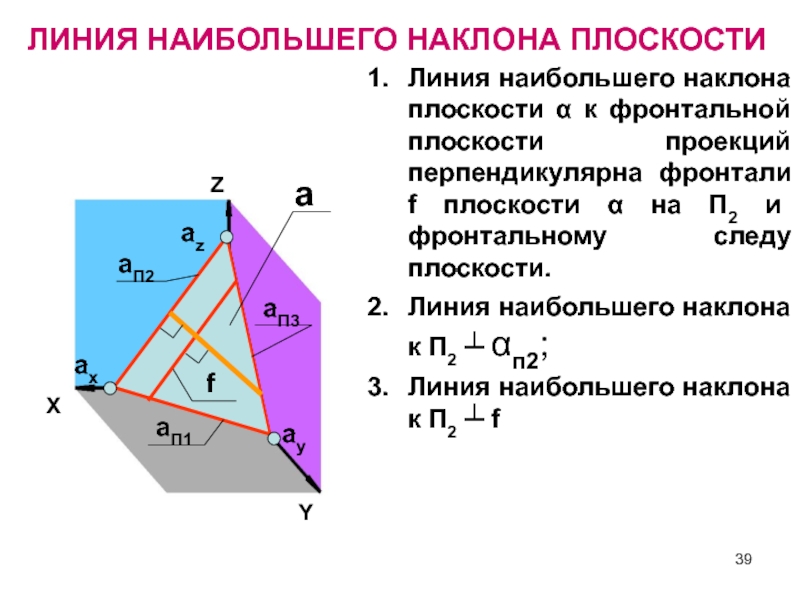
Линия наибольшего наклона плоскости α к фронтальной
плоскости проекций перпендикулярна фронтали f плоскости α на П2 и
фронтальному следу плоскости.Линия наибольшего наклона к П2 ┴ αп2;
Линия наибольшего наклона к П2 ┴ f
Y
f
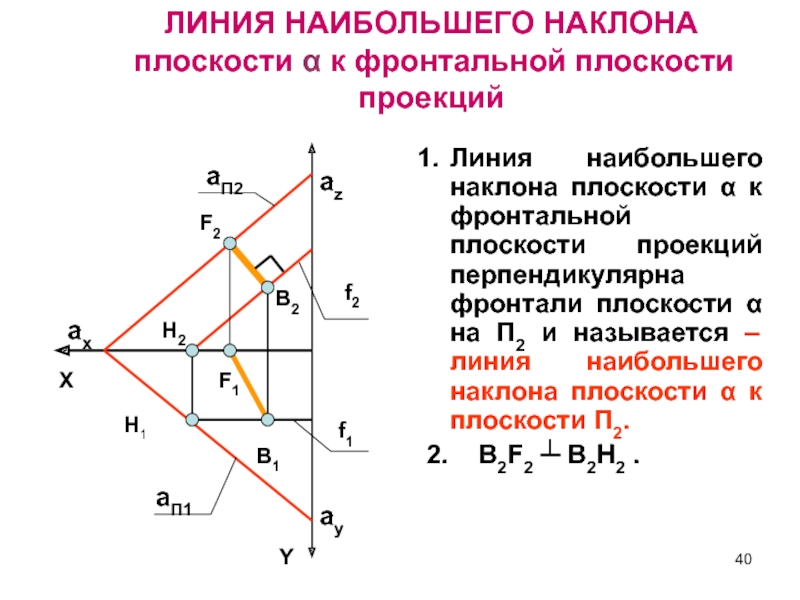
Слайд 40Линия наибольшего наклона плоскости α к фронтальной плоскости проекций перпендикулярна
фронтали плоскости α на П2 и называется – линия наибольшего
наклона плоскости α к плоскости П2.2. В2F2 ┴ B2H2 .
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости α к фронтальной плоскости проекций
aП2
aП1
Y
ax
В2
В1
f2
f1
H2
H1
X
az
ay
F1
F2
Слайд 41А2
F2
В2
А1
F1
ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА
плоскости ΔАВС к фронтальной плоскости проекций
1.
Линия наибольшего наклона плоскости ΔАВС к фронтальной плоскости проекций перпендикулярна
фронтали плоскости ΔАВС на П2 и называется –линия наибольшего наклона плоскости ΔАВС к П2.
2. В2D2 ┴ C2F2
X
D2
D1
В1
С1
С2
Слайд 42 Пример.
Построить проекции равнобедренного треугольника ΔАВС принадлежащего плоскости α, заданной
следами. αx(110,0,0); αП2 ^оx=30°; αП1^оx=45°; А(50,?,20).
Основание АВ принадлежит горизонтали
плоскости.IАВI=40мм, высота треугольника 30мм.
Слайд 44
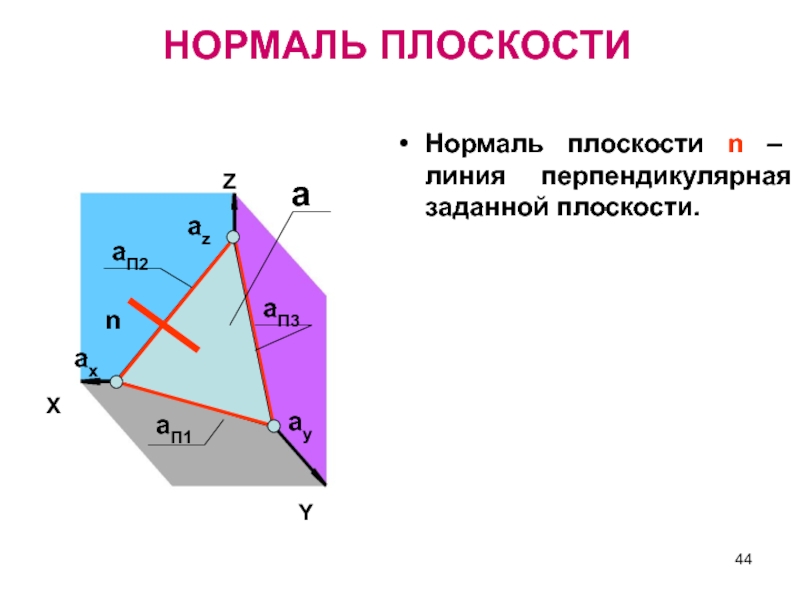
НОРМАЛЬ ПЛОСКОСТИ
Нормаль плоскости n – линия перпендикулярная заданной плоскости.
Z
X
aП1
aП3
aП2
ax
ay
az
Y
a
n
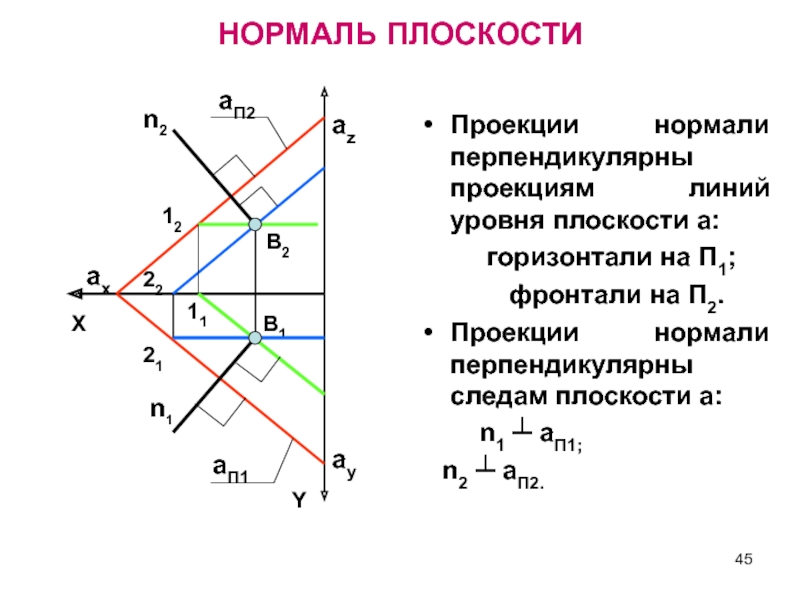
Слайд 45Проекции нормали перпендикулярны проекциям линий уровня плоскости a:
горизонтали на П1;
фронтали на П2.Проекции нормали перпендикулярны следам плоскости a:
n1 ┴ aП1;
n2 ┴ aП2.
НОРМАЛЬ ПЛОСКОСТИ
aП1
Y
ax
В2
В1
n2
n1
X
az
ay
aП2
12
11
21
22
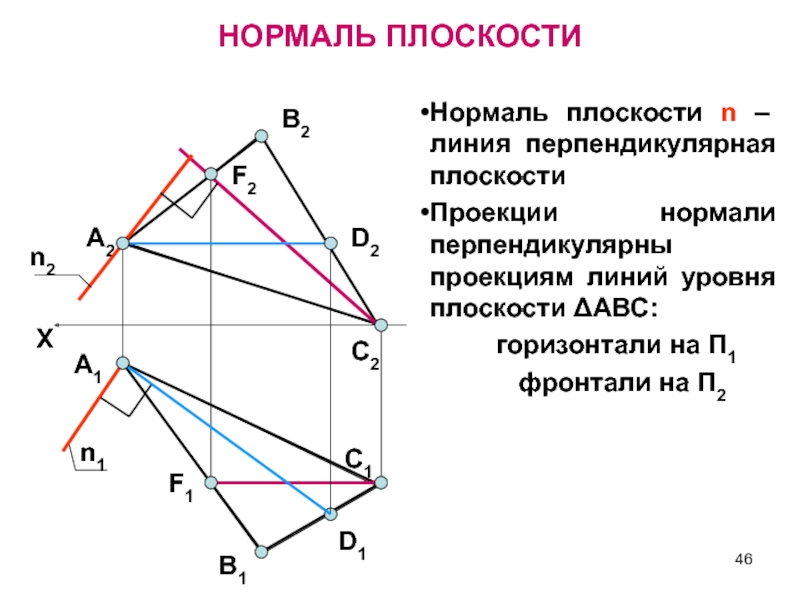
Слайд 46НОРМАЛЬ ПЛОСКОСТИ
Нормаль плоскости n – линия перпендикулярная плоскости
Проекции нормали
перпендикулярны проекциям линий уровня плоскости ΔАВС:
горизонтали на П1фронтали на П2
А2
F2
В2
А1
F1
X
D2
D1
В1
С1
С2
n2
n1