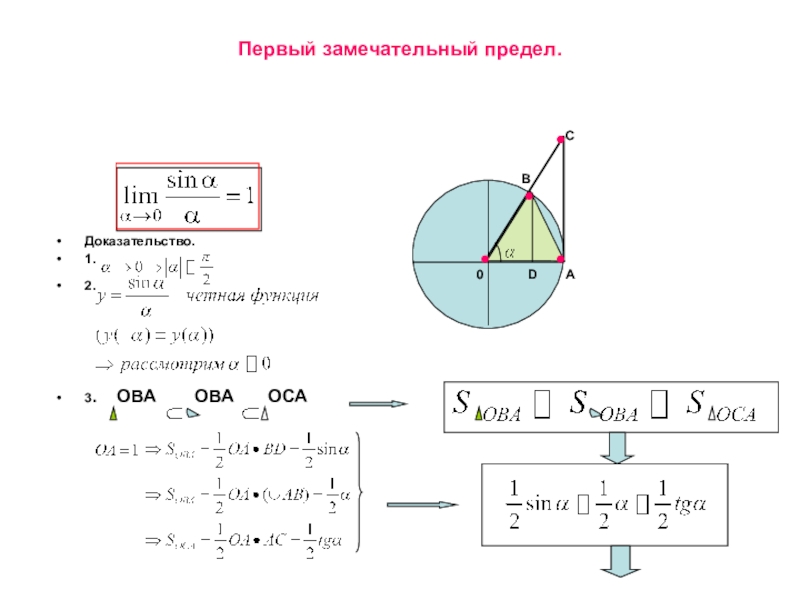
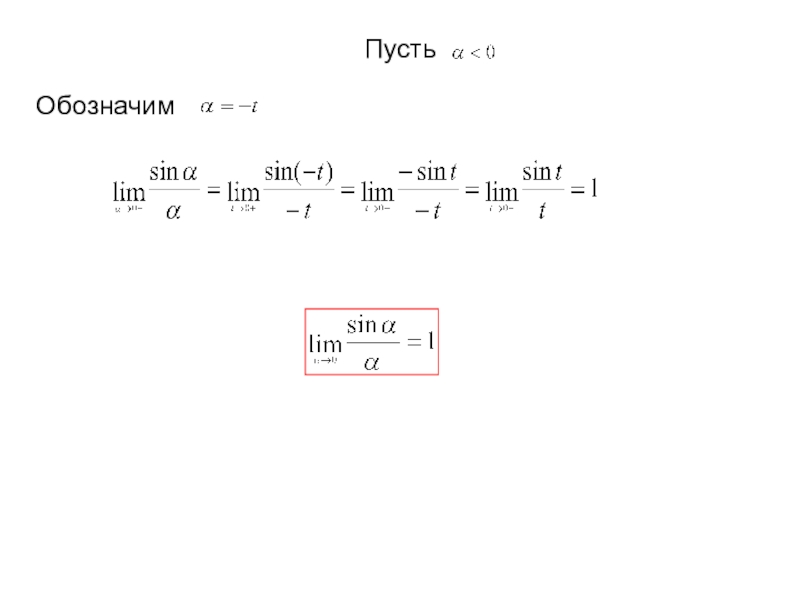
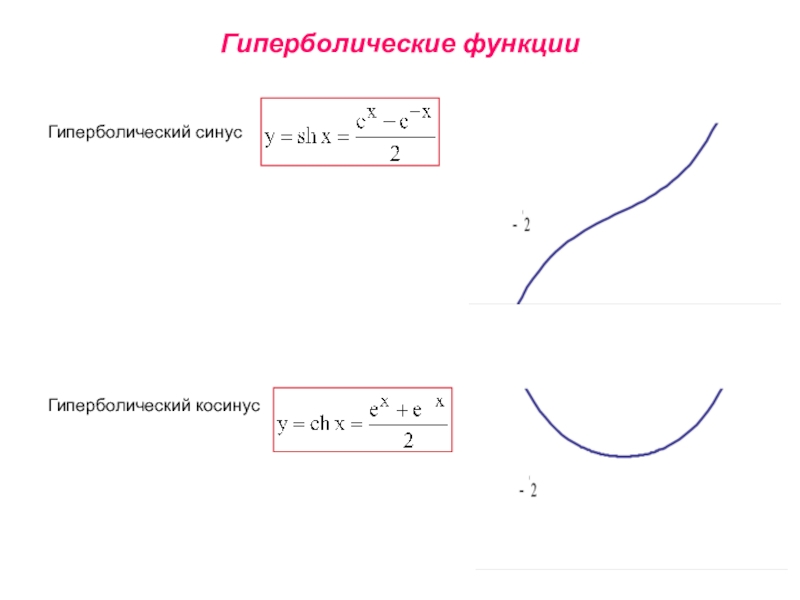
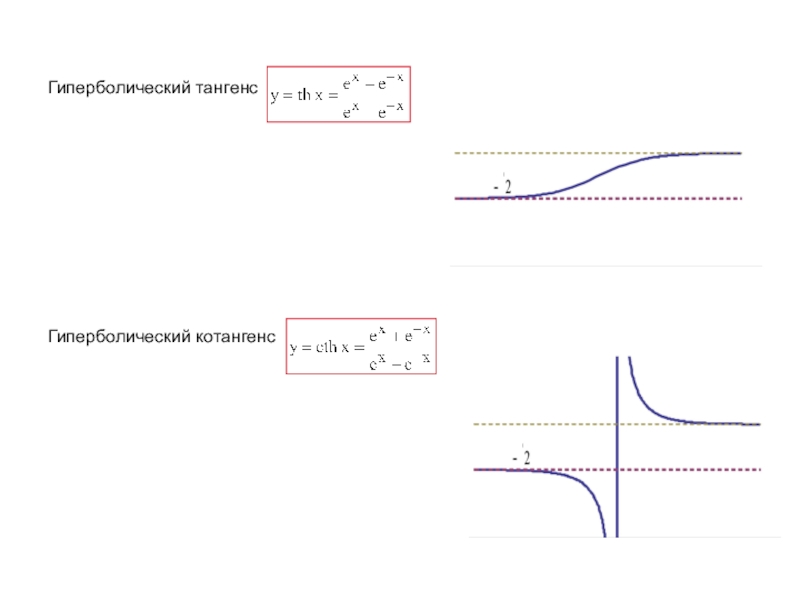
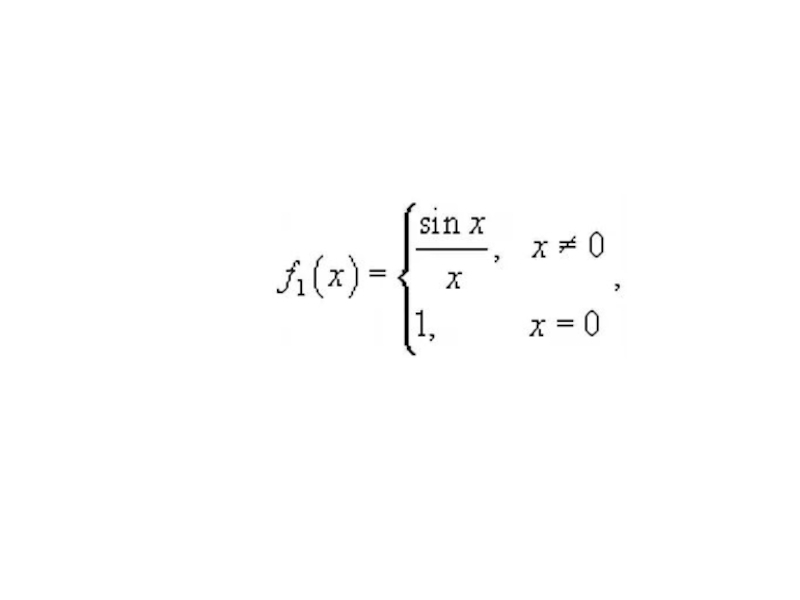Ограниченность функции, имеющей предел

Содержание

1. Ограниченность функции, имеющей предел
2. Слайд 2
3. Теорема (о разности между функцией
4. Доказательство прямой теоремы.Доказательство обратной теоремы.где - бесконечно малаяпри
5. Бесконечно малые величины.(Повторение)Переменная
6. Основные свойства бесконечно малых величин.
7. СВОЙСТВА ПРЕДЕЛОВ.Пусть существуютТогда:1.2.3. ЕслитоДоказательство 1 свойства.1.где
8. Свойства пределов (продолжение)4. Предел постоянной равен самой постоянной. 5. Постоянной множитель можно выносить за знак предела.
9. Бесконечно большие величины.4. Бесконечно большие величины при
10. Пример2x+5 является бесконечно большой величиной при
11. Теорема 2.Доказательство.1. Возьмем произвольное и обозначим 2.
12. 5. Бесконечно большие при .Определение.Геометрическая интерпретация.0хyMN-Nх
13. Типы неопределенностейВычислить пределСуществуют неопределенности вида
14. Признаки существования пределов.Теорема 1.ПустьГеометрическая интерпретация.Теорема 2 (теорема Вейерштрасса).Пусть1.2.0хy
15. Первый замечательный предел.Доказательство.1.2.3. OBA OBA OCA0ABCD
16. 4.5.6. По первому признаку существования предела:
17. Пусть Обозначим
18. Второй замечательный предел.1.2. Утверждения:3. По второму признаку существования предела:
19. Следствия второго замечательного предела.1). Если x – действительное число, то
20. Натуральные логарифмы.Логарифмы с основанием e называются натуральными логарифмами.
21. Гиперболические функцииГиперболический синус
22. Гиперболический тангенс
23. Из определений следуют формулы:
24. Сравнение бесконечно малых.Определения.Пусть
25. Сравнение бесконечно малых.Свойства эквивалентных бесконечно малых.1.2.3.4.Доказательство свойства
26. Доказательство свойства 3: предел бесконечно малых не изменится, если их заменить на эквивалентныетакт так как и
27. Свойство 5Если есть бесконечно
28. Практический выводПри раскрытии неопределенности типа
29. Таблица эквивалентных бесконечно малыхПри1.
30. Продолжение таблицы эквивалентных бесконечно малых4.5. 6. так как
31. Продолжение таблицы эквивалентных бесконечно малыхАналогично докажем7.Замена
32. Продолжение таблицы эквивалентных бесконечно малых10.
33. Пример
34. Сравнение бесконечно малых.Примеры.1.2.3.
35. Слайд 35
36. Слайд 36
37. Слайд 37
38. Определение 1 на языке Y=f(x) называется непрерывной
39. Наличие
40. Из определения следует, что в точке непрерывности
41. Определение 2 (следующий слайд)
42. Слайд 42
43. Рисунок ко второму определению непрерывности
44. Слайд 44
45. Слайд 45
46. Оба определения непрерывности функции в точке эквивалентны.Доказательство.
47. Непрерывность основных элементарных функций в точках области
48. Теоремы о непрерывности суммы, разности, произведения и частного двух непрерывных функций
49. Доказательство для произведения.Пусть
50. Слайд 50
51. Слайд 51
52. Слайд 52
53. Слайд 53
54. Слайд 54
55. Слайд 55
56. Слайд 56
57. Пример
58. Пример
59. Слайд 59
60. ПримерРассмотрим функцию
61. Слайд 61
62. Слайд 62
63. Слайд 63
64. Слайд 64
65. Слайд 65
66. Слайд 66
67. Слайд 67
68. Слайд 68
69. Если функция непрерывна на замкнутом интервале, то она достигает на нем своего наибольшего и наименьшего значений.
70. Слайд 70
71. Если функция непрерывна на замкнутом интервале, то
72. Слайд 72
73. Скачать презентанцию

Теорема (о разности между функцией и ее пределом) 1. Прямая теорема:(необходимость)2. Обратная теорема: (достаточность)где - бесконечно малаяпригде - бесконечно

Главная
Разное
Ограниченность функции, имеющей предел

Слайды и текст этой презентации

Слайд 1 Ограниченность функции, имеющей предел.
Определение.

Функция

называется

ограниченной на

множестве D, если

Теорема.

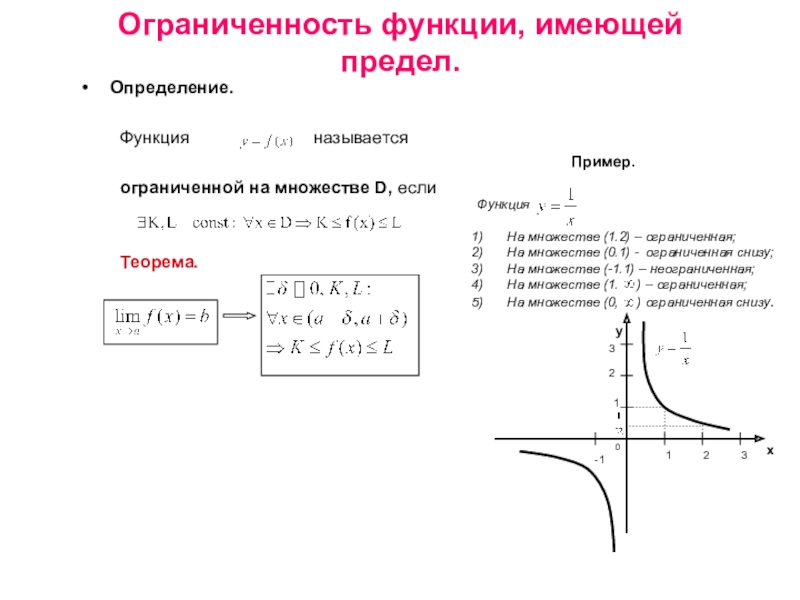
Пример.

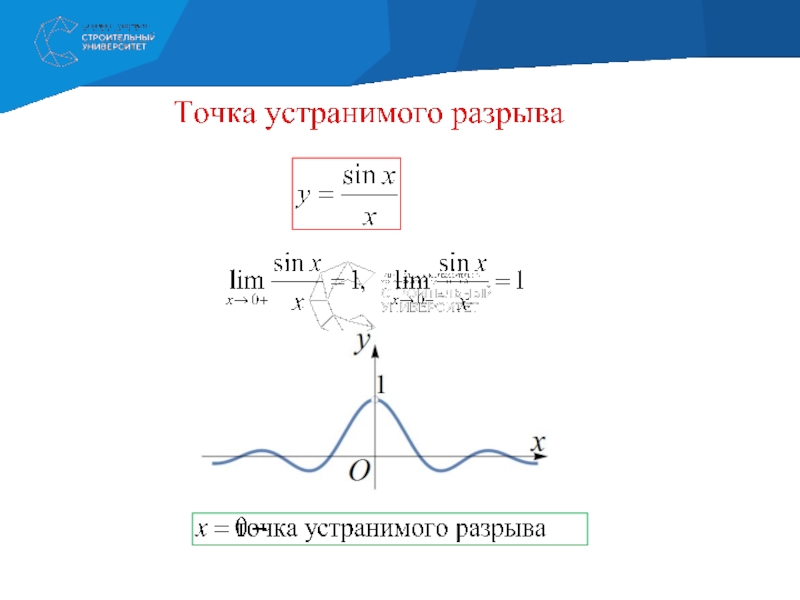
Функция

На множестве (1.2) – ограниченная;
На множестве (0.1) - ограниченная снизу;
На множестве (-1.1) – неограниченная;
На множестве (1. ) – ограниченная;
На множестве (0, ) ограниченная снизу.

-1

Ограниченность функции, имеющей предел. Определение.Функция

Слайд 2

Слайд 3 Теорема (о разности между функцией и ее пределом)

1. Прямая теорема:
(необходимость)

2.

Обратная теорема:
(достаточность)

где - бесконечно малая
при
где

- бесконечно малая
при

где - бесконечно малая
при

Теорема (о разности между функцией и ее пределом) 1. Прямая теорема:(необходимость)2. Обратная теорема: (достаточность)где

Слайд 4Доказательство прямой теоремы.

Доказательство обратной теоремы.

где

- бесконечно малая
при

Слайд 5Бесконечно малые величины.(Повторение)
Переменная называется бесконечно

малой величиной при ,

если

То есть

Например,

(Геометрическую интерпретацию бесконечно малой величины см. ранее, при
определении предела).

Слайд 6Основные свойства бесконечно малых величин.

Пусть

и

- бесконечно малые
при
Тогда при
1. - бесконечно малая величина.
2. -бесконечно малая величина.
3. - бесконечно малая величина, если ограниченная функция.

Доказательство 1 свойства (для суммы).
1.Обозначим
2.Возьмем число ,где произвольное
положительное число.
3.Из определения бесконечно малых величин следует:

Тогда

Д.з. Докажите
свойство 3.

Основные свойства бесконечно малых величин. Пусть и

Слайд 7СВОЙСТВА ПРЕДЕЛОВ.
Пусть существуют

Тогда:
1.

2.

3. Если

то

Доказательство 1 свойства.

1.

где

и -

бесконечно малые при

2.

Следовательно

число

бесконечно малая

Д.з. Докажите
свойство 2.

СВОЙСТВА ПРЕДЕЛОВ.Пусть существуютТогда:1.2.3. ЕслитоДоказательство 1 свойства.1.где и

Слайд 8Свойства пределов (продолжение)
4. Предел постоянной равен самой постоянной.

5. Постоянной

множитель можно выносить за знак предела.

Слайд 9Бесконечно большие величины.
4. Бесконечно большие величины при

.

Определение.
Функция

называется
бесконечно большой при
если

Связь бесконечно больших
и бесконечно малых величин.
Теорема 1.
Если - бесконечно большая величина при ,
то - бесконечно малая величина.

-M

Бесконечно большие величины.4. Бесконечно большие величины при .Определение.Функция

Слайд 10Пример

2x+5 является бесконечно большой величиной при

Слайд 11Теорема 2.

Доказательство.
1. Возьмем произвольное
и обозначим
2. Так как

,то

Следовательно

Если - бесконечно малая величина при

то - бесконечно большая величина.

Теорема 2.Доказательство.1. Возьмем произвольное и обозначим 2. Так как

Слайд 125. Бесконечно большие при

.
Определение.

Геометрическая интерпретация.
0
х
y
M
N
-N
х

Слайд 13Типы неопределенностей
Вычислить предел

Существуют неопределенности вида

Слайд 14Признаки существования пределов.

Теорема 1.
Пусть

Геометрическая интерпретация.
Теорема 2 (теорема Вейерштрасса).
Пусть
1.

2.
0
х
y

Слайд 15Первый замечательный предел.

Доказательство.
1.
2.

3. OBA OBA

OCA
0
A
B
C
D

Слайд 164.

5.

6. По первому признаку существования предела:

Слайд 17Пусть
Обозначим

Слайд 18Второй замечательный предел.

1.

2. Утверждения:

3. По второму признаку существования предела:

Слайд 19Следствия второго замечательного предела.
1). Если x – действительное число, то

Слайд 20Натуральные логарифмы.
Логарифмы с основанием e называются натуральными логарифмами.

Слайд 21Гиперболические функции

Гиперболический синус

Гиперболический косинус

Слайд 22
Гиперболический тангенс

Гиперболический котангенс

Слайд 23Из определений следуют формулы:

Слайд 24Сравнение бесконечно малых.
Определения.
Пусть

- бесконечно

малые при
Тогда:
1. Если , то говорят,
что бесконечно малая имеет более
высокий порядок малости, чем
2. Если , то говорят,
что бесконечно малая имеет
более высокий порядок малости, чем
3. Если
, то говорят, что бесконечно малые
имеют одинаковый порядок малости.

4. Если ,то бесконечно малые
называются эквивалентными.

Обозначение: