Операции над графами

Содержание

1. Операции над графами
2. 1. Объединение Граф Н называется объединением (наложением)
3. Слайд 3
4. Слайд 4
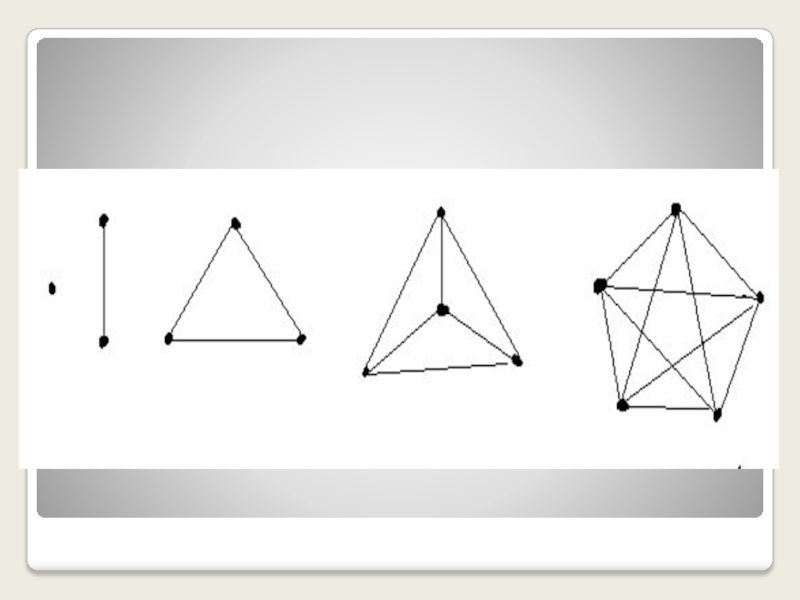
5. Граф G называется полным, если любые
6. Слайд 6
7. С помощью операции произведения вводится n -мерный
8. Граф порядка 2п, вершины которого можно представить
9. 3. Удаление вершинГраф H называется подграфом гр
10. Слайд 10
11. Скачать презентанцию

1. Объединение Граф Н называется объединением (наложением) графов F и G , т.е. H=FG, если VH=VFVG, EH=EFEG

Слайды и текст этой презентации

Слайд 1Операции над графами

Слайд 21. Объединение Граф Н называется объединением (наложением) графов F и G

, т.е. H=FG, если VH=VFVG, EH=EFEG

Слайд 3
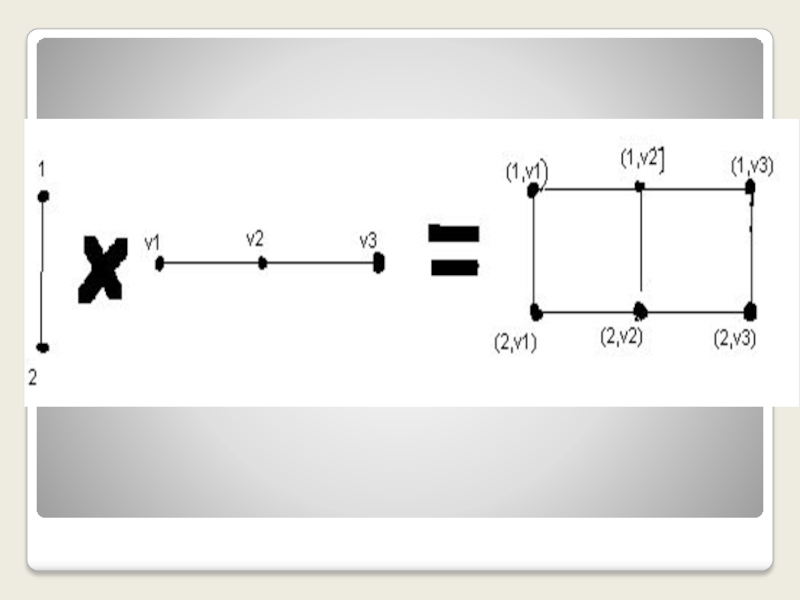
2. Произведение
Граф G называется произведением графов G1 и G2 (G=G1×G2),

если VG=V1×V2 – декартово произведение множеств вершин исходных графов, а

EG определяется следующим образом: вершины (u1,u2) и (v1,v2) смежны в графе тогда и только тогда, когда () или u1= v1, а u2 и v2смежны в G2,
или u2=v2, а u1 и v1 смежны в G1

G1×G2= G1 G2, E(G1×G2)= G1E(G2)+G2E(G1),

2. ПроизведениеГраф G называется произведением графов

Слайд 4

Слайд 5
Граф G называется полным, если любые две его вершины

смежны, т.е. EG=(VG)(2).
Полный граф порядка n обозначается Kn, число ребер

в нем равно

Граф G называется полным, если любые две его вершины смежны, т.е. EG=(VG)(2).Полный граф порядка n обозначается

Слайд 6

Слайд 7С помощью операции произведения вводится n -мерный куб Qn :
Q1=K2

, Qn= K2 × Qn-1, n>1.

Слайд 8Граф порядка 2п, вершины которого можно представить (0, 1) –векторами

длины n таким образом, что две вершины будут смежны 

соответ ствующие векторы различаются ровно в одной координате. Поскольку каждая вершина n -мерного куба Qn инцидентна n ребрам, то число его ребер равно n2 n-1.