Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Описанная окружность
Содержание
- 1. Описанная окружность
- 2. DВСЕсли все вершины многоугольника лежат на окружности,
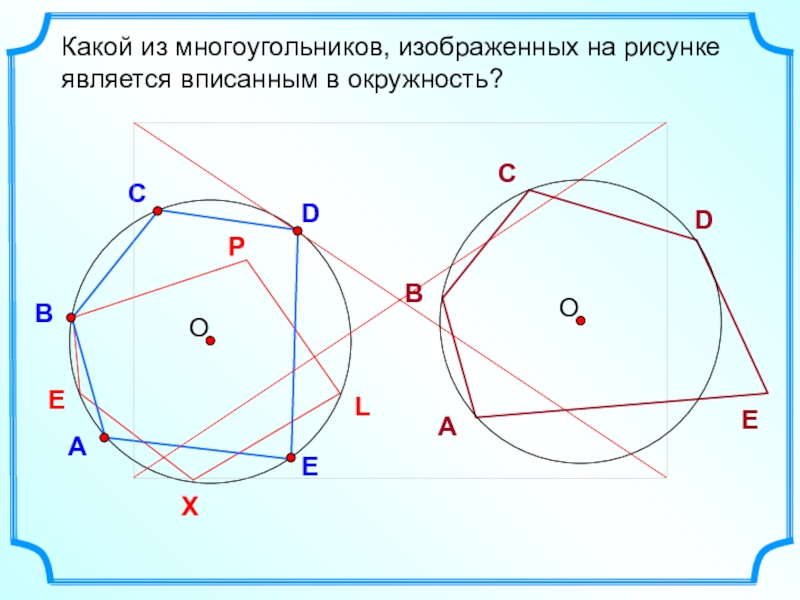
- 3. DВСКакой из многоугольников, изображенных на рисунке является вписанным в окружность?АELPXE
- 4. АВDСвойство вписанного четырехугольника В любом вписанном четырехугольнике
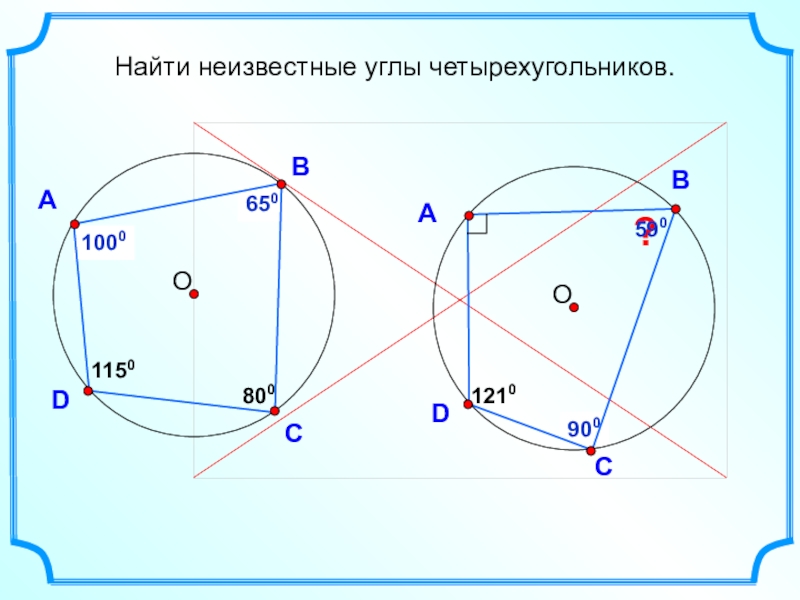
- 5. ?590?900?650?1000DАВС8001150DАВС1210Найти неизвестные углы четырехугольников.
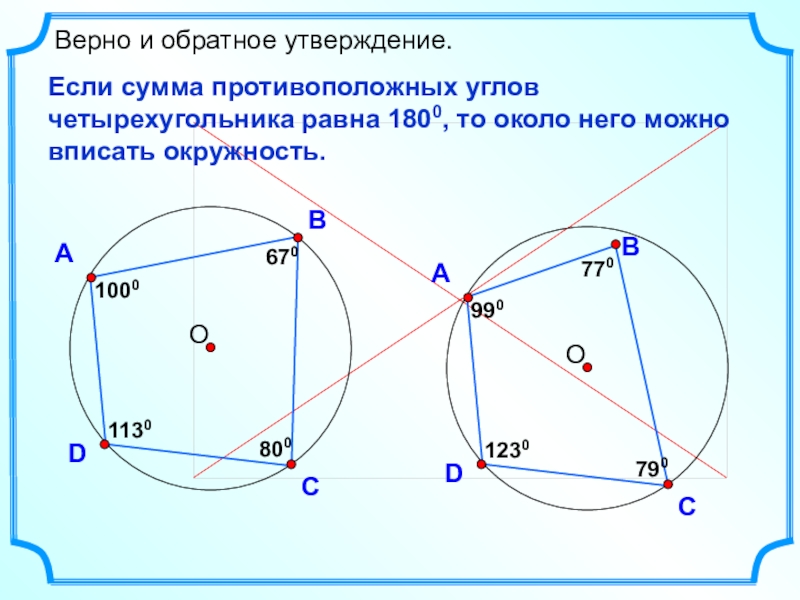
- 6. DВерно и обратное утверждение.Если сумма противоположных углов четырехугольника равна 1800, то около него можно вписать окружность.АВС80010001130670
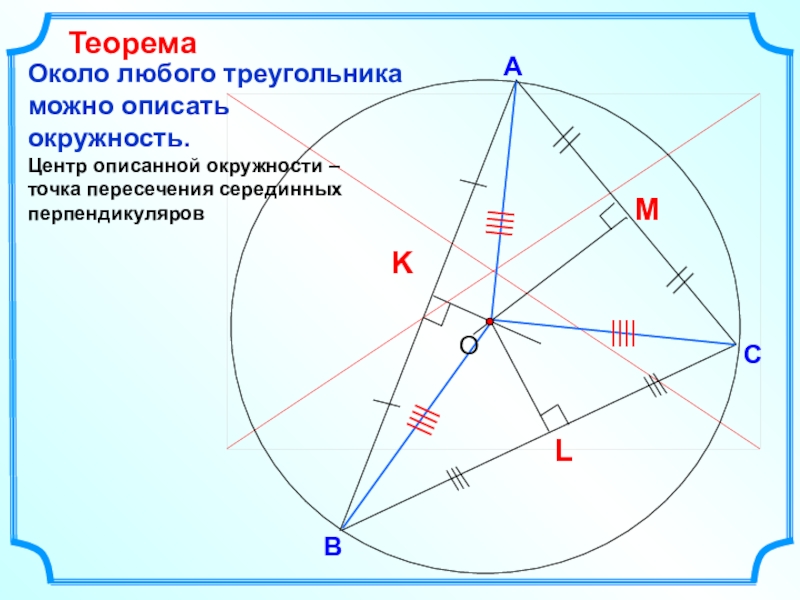
- 7. ВСАОколо любого треугольника можно описать окружность.Центр описанной окружности – точка пересечения серединных перпендикуляровТеорема
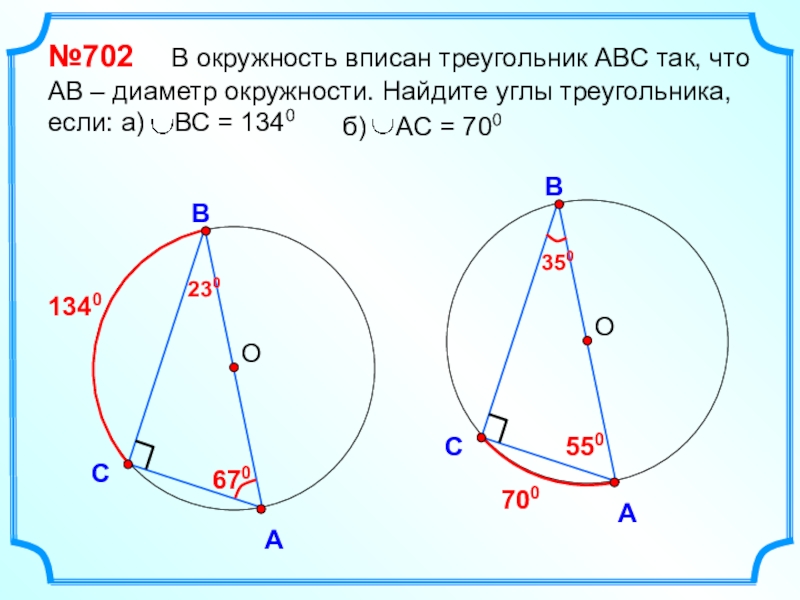
- 8. ОВСА№702 В окружность вписан треугольник
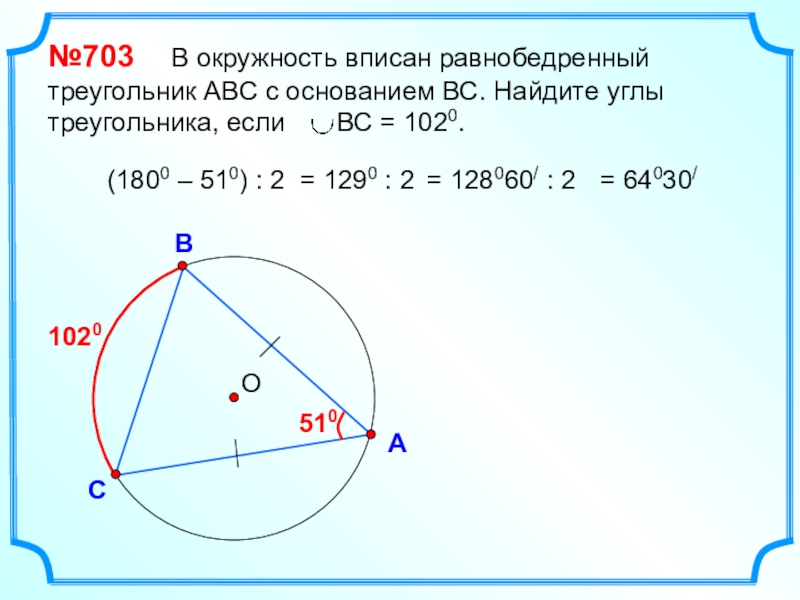
- 9. ОВСА№703 В окружность вписан равнобедренный
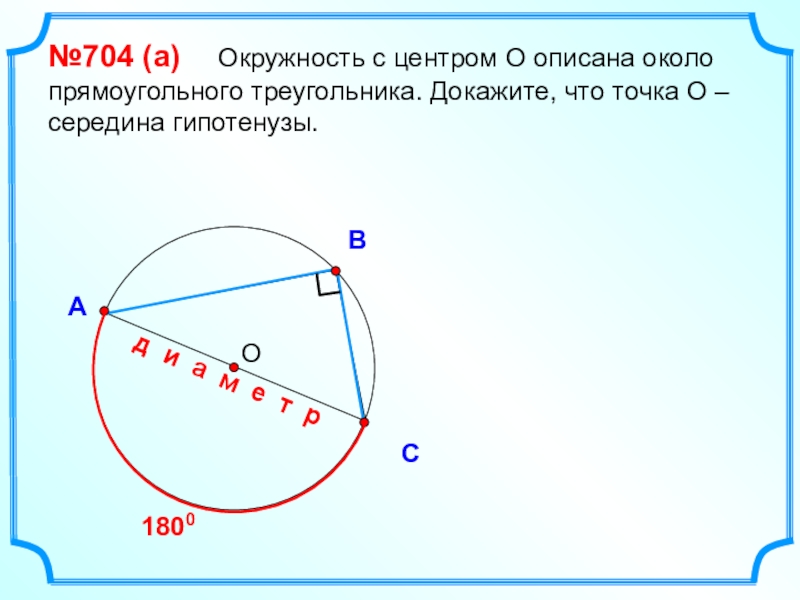
- 10. ВСА№704 (a) Окружность с центром
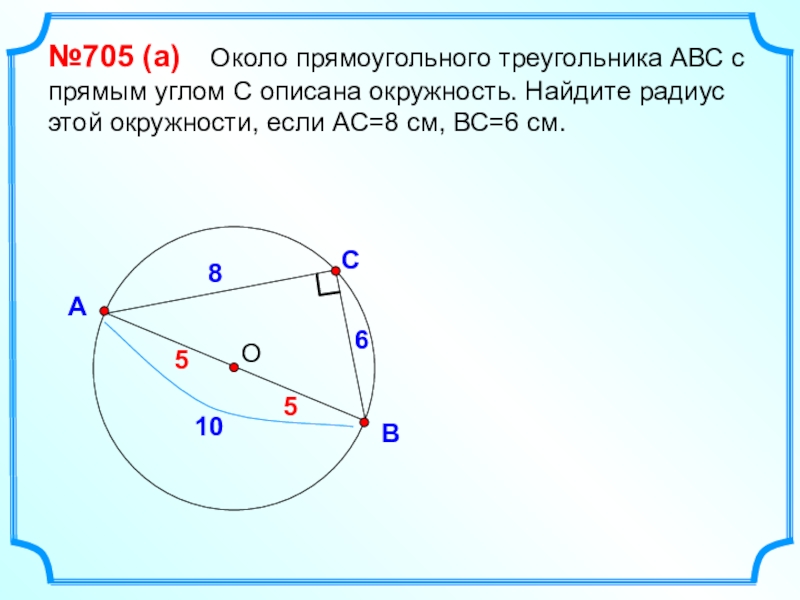
- 11. СВА№705 (а) Около прямоугольного треугольника АВС
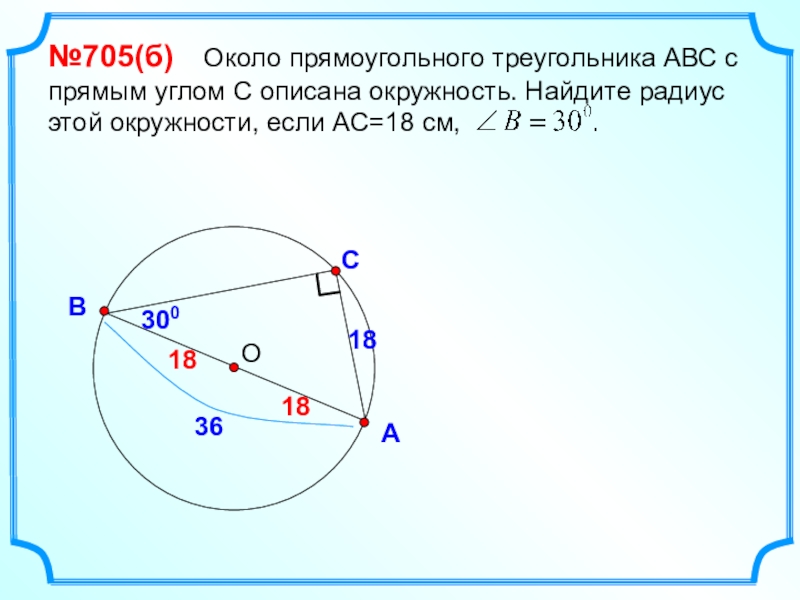
- 12. САВ№705(б) Около прямоугольного треугольника АВС с
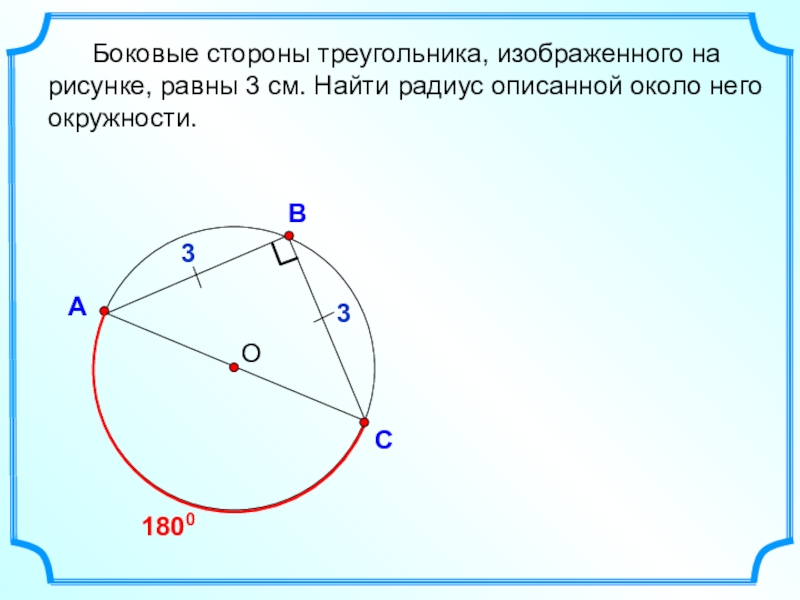
- 13. ОВСА Боковые стороны треугольника, изображенного
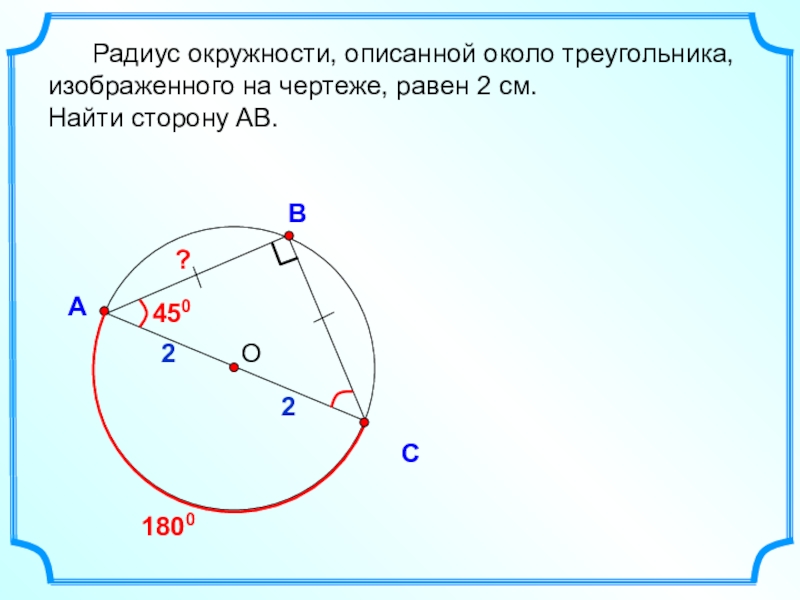
- 14. ОВСА Радиус окружности, описанной около
- 15. Домашнее задание: П.78, решить № 706,707Спасибо за урок!
- 16. Скачать презентанцию
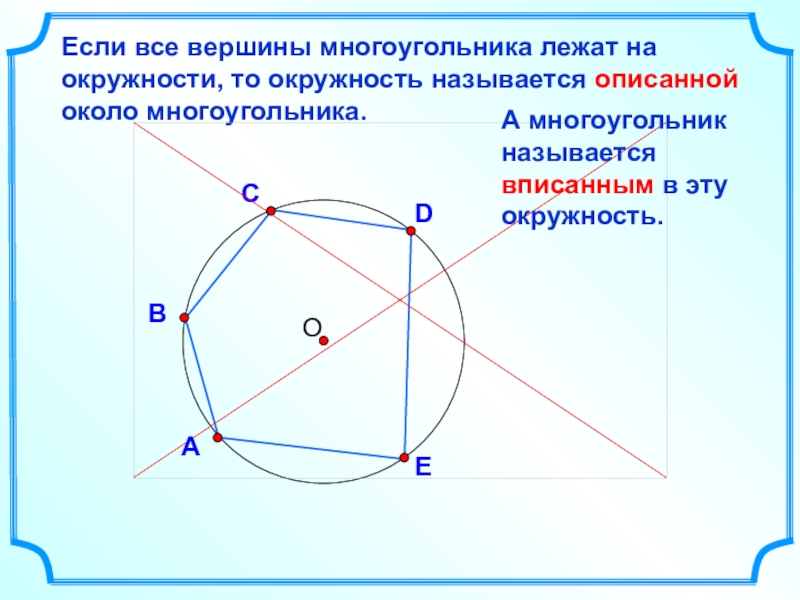
DВСЕсли все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника.АEА многоугольник называется вписанным в эту окружность.
Слайды и текст этой презентации
Слайд 2D
В
С
Если все вершины многоугольника лежат на окружности, то окружность называется
описанной около многоугольника.
Слайд 4А
В
D
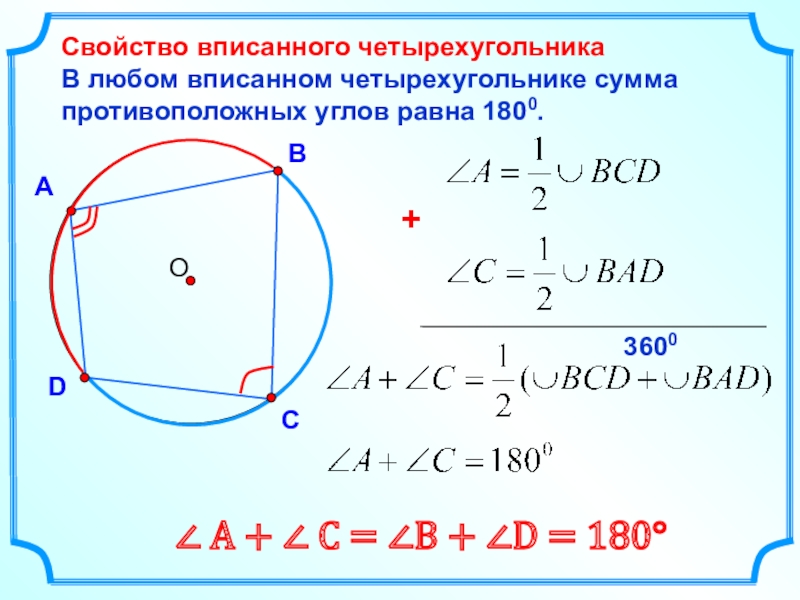
Свойство вписанного четырехугольника
В любом вписанном четырехугольнике сумма противоположных углов
равна 1800.
∠ А
+ ∠ C = ∠В + ∠D = 180°С
3600
Слайд 6D
Верно и обратное утверждение.
Если сумма противоположных углов четырехугольника равна 1800,
то около него можно вписать окружность.
А
В
С
800
1000
1130
670
Слайд 7В
С
А
Около любого треугольника можно описать
окружность.
Центр описанной окружности –
точка
пересечения серединных перпендикуляров
Теорема
Слайд 8О
В
С
А
№702 В окружность вписан треугольник АВС так, что
АВ – диаметр окружности. Найдите углы треугольника, если: а)
ВС = 13401340
670
230
700
550
350
Слайд 9О
В
С
А
№703 В окружность вписан равнобедренный треугольник АВС с
основанием ВС. Найдите углы треугольника, если ВС
= 1020.1020
510
(1800 – 510) : 2
= 1290 : 2
= 128060/ : 2
= 64030/
Слайд 10В
С
А
№704 (a) Окружность с центром О описана около
прямоугольного треугольника. Докажите, что точка О – середина гипотенузы.
1800
д и
а м е т р
Слайд 11С
В
А
№705 (а) Около прямоугольного треугольника АВС с прямым углом
С описана окружность. Найдите радиус этой окружности, если АС=8 см,
ВС=6 см.8
6
Слайд 12С
А
В
№705(б) Около прямоугольного треугольника АВС с прямым углом С
описана окружность. Найдите радиус этой окружности, если АС=18 см,
18
300
Слайд 13О
В
С
А
Боковые стороны треугольника, изображенного на рисунке, равны
3 см. Найти радиус описанной около него окружности.
1800
3
3
Слайд 14О
В
С
А
Радиус окружности, описанной около треугольника, изображенного на
чертеже, равен 2 см.
Найти сторону АВ.
1800
2
2
450
?
