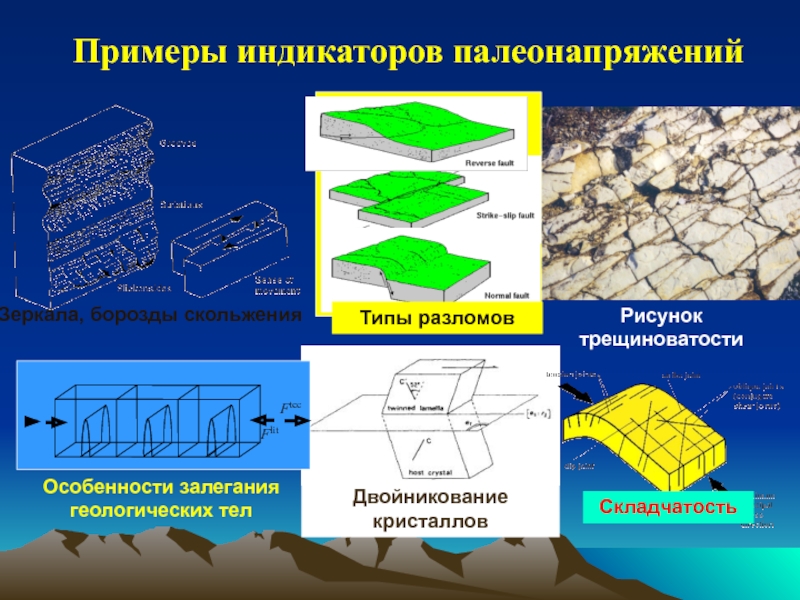
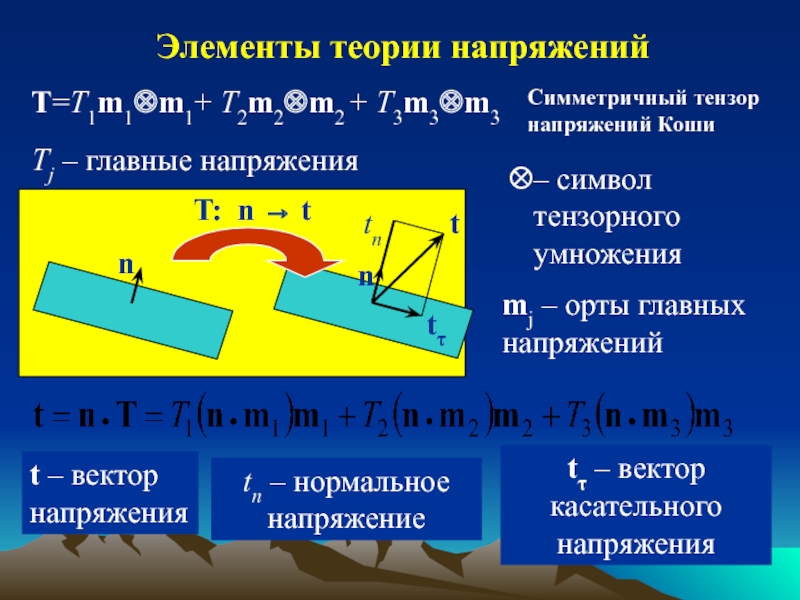
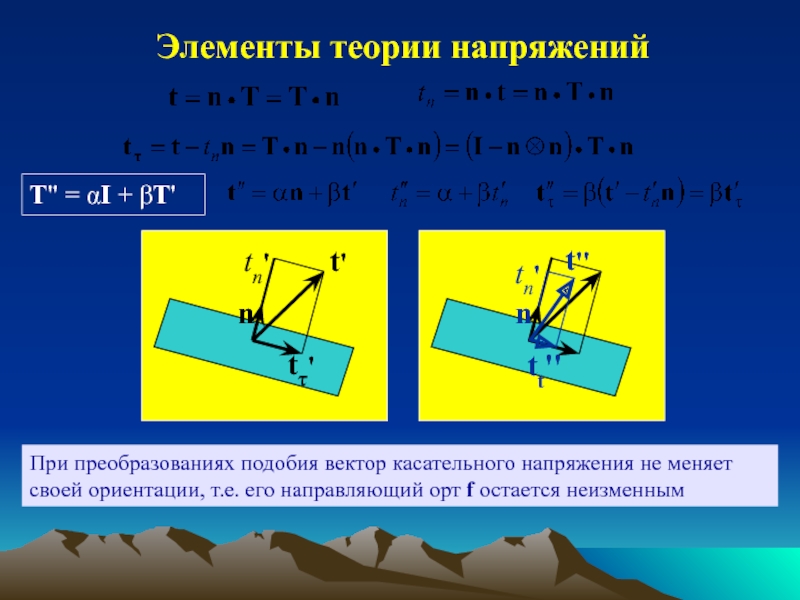
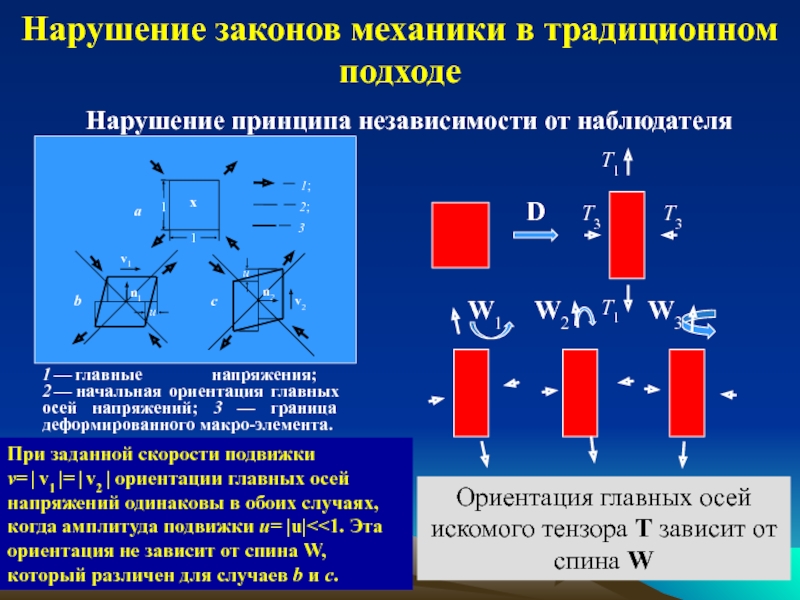
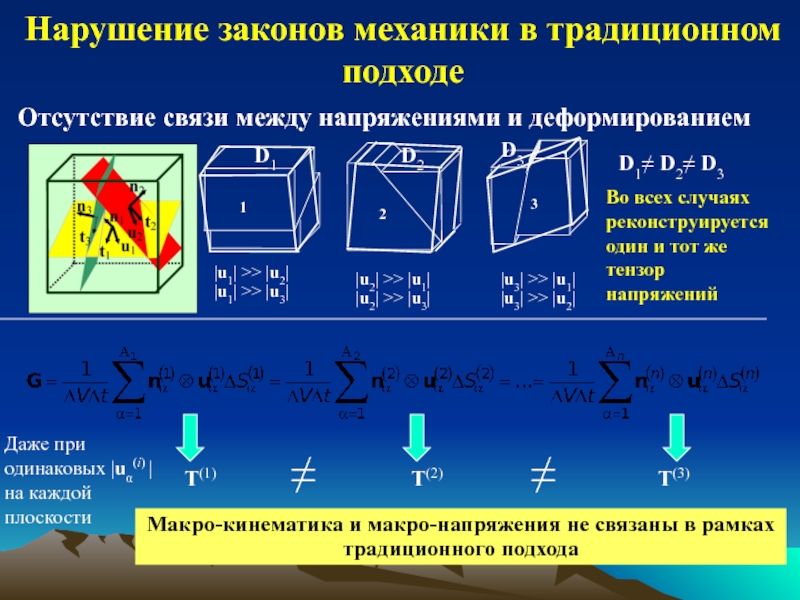
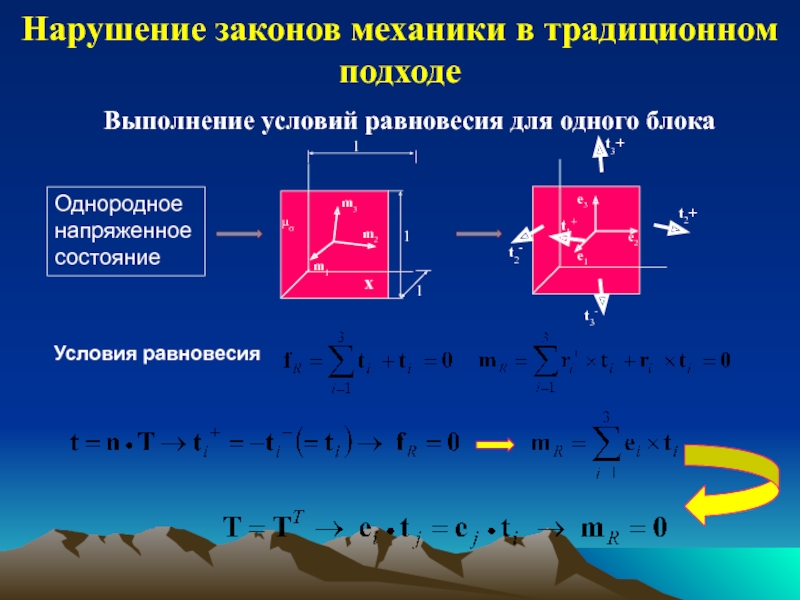
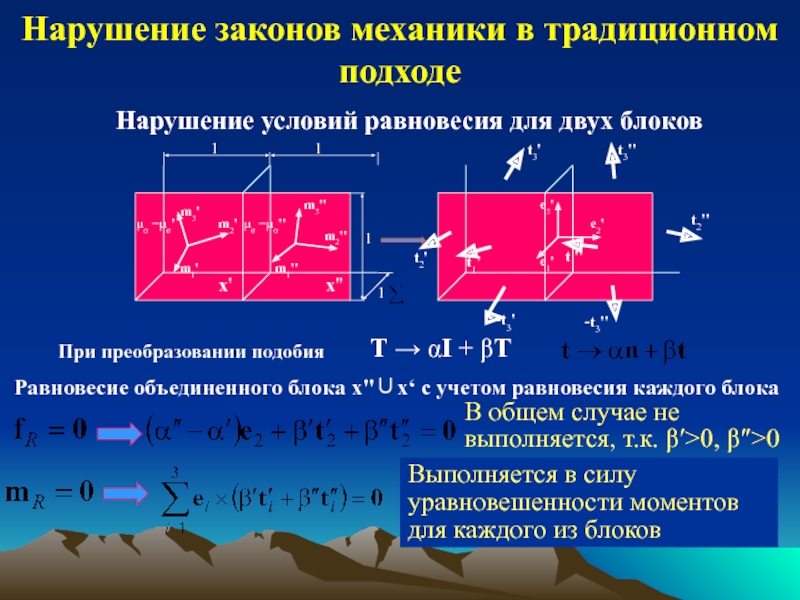
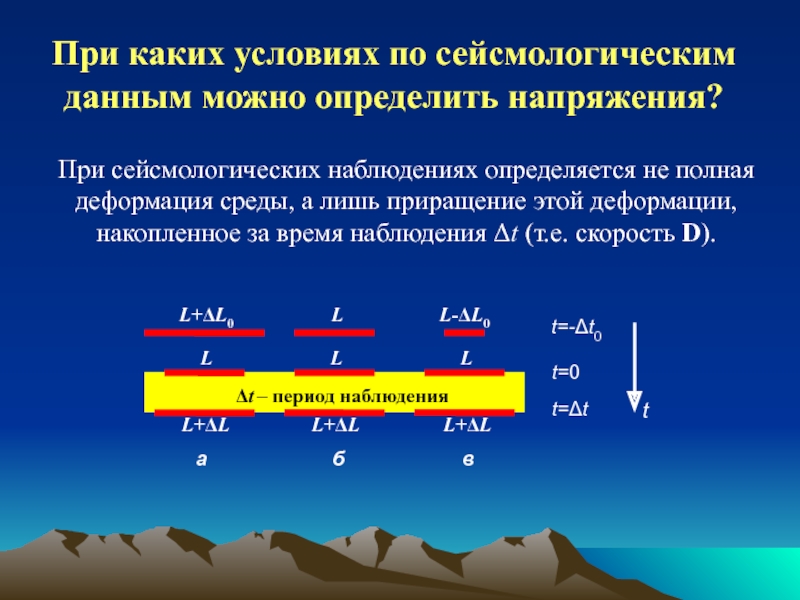
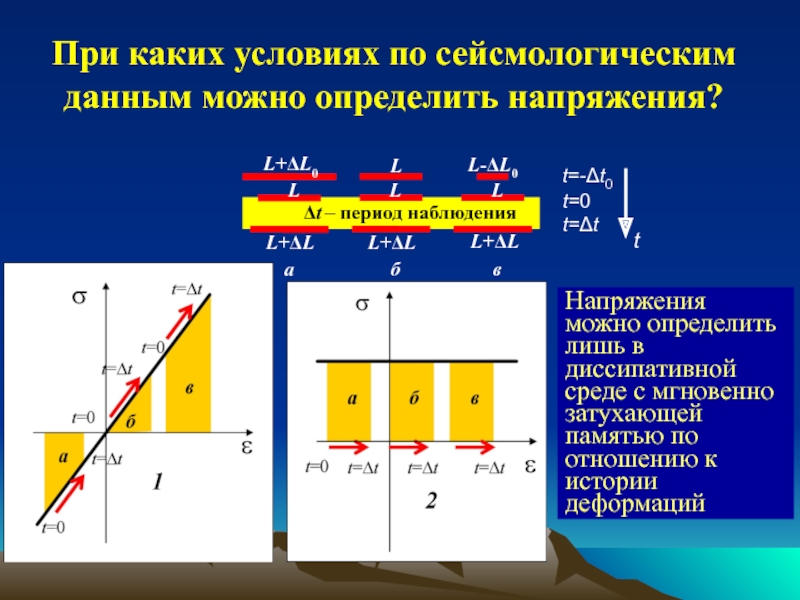
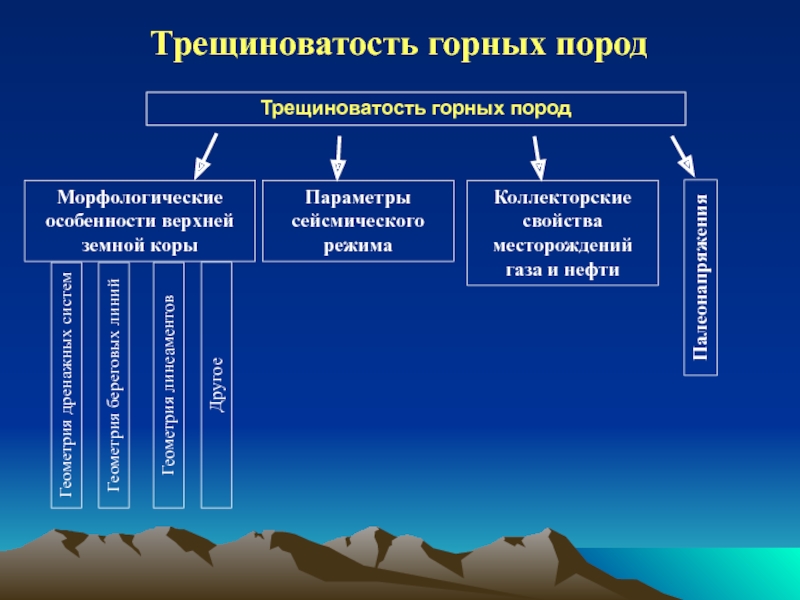
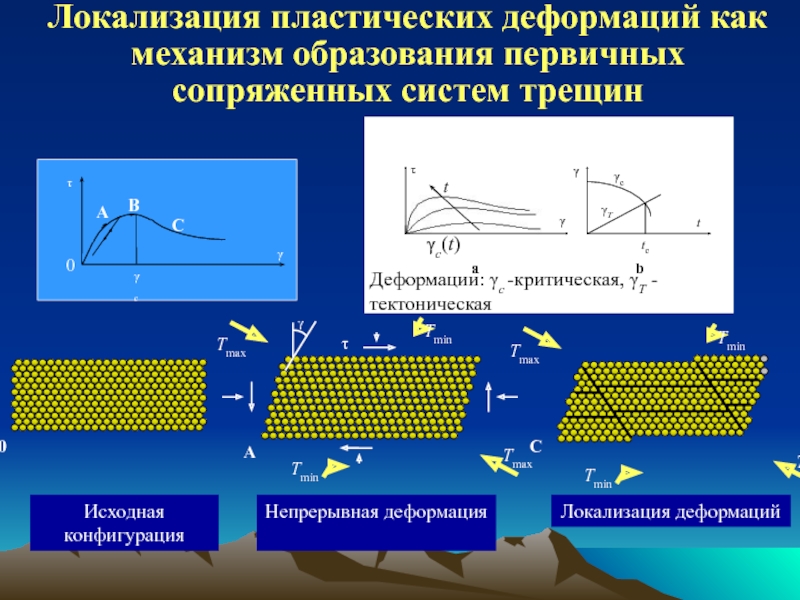
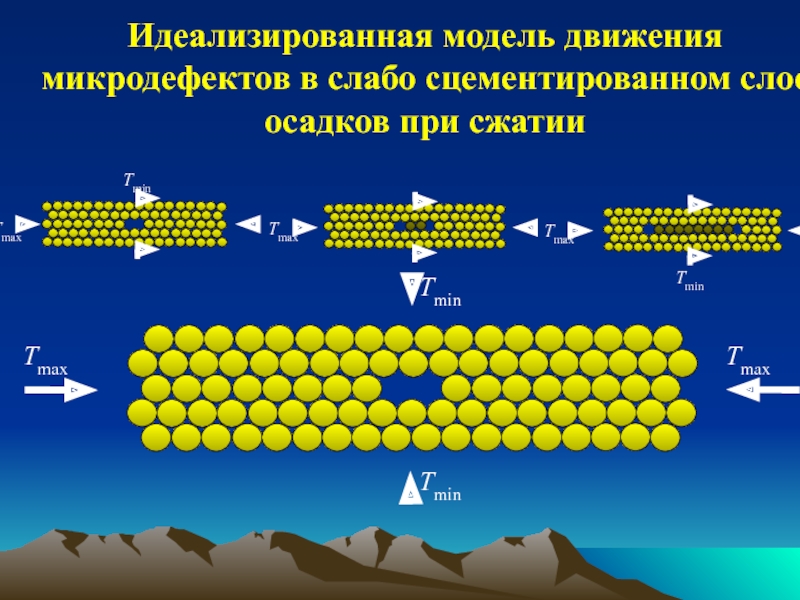
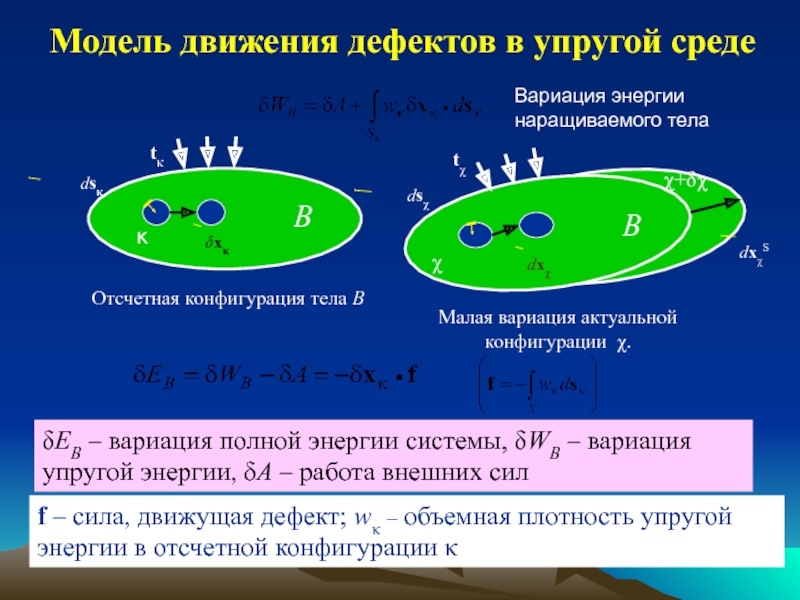
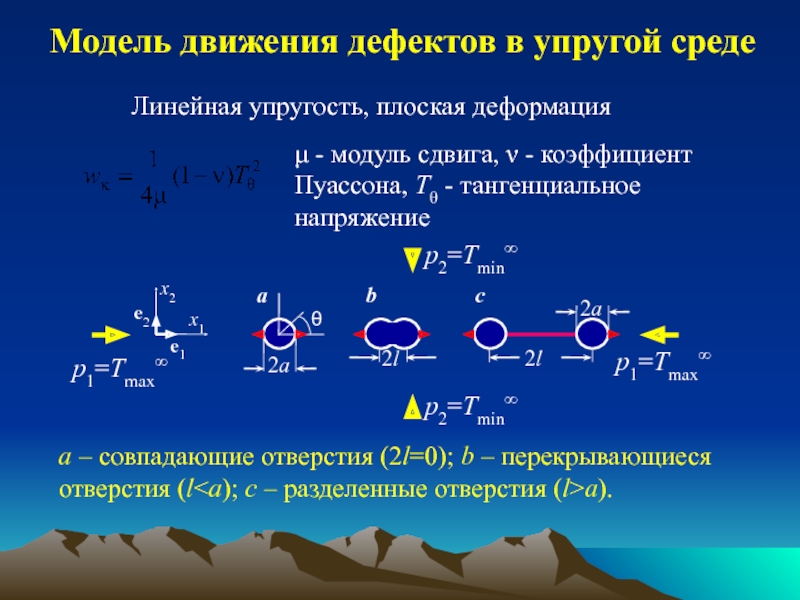
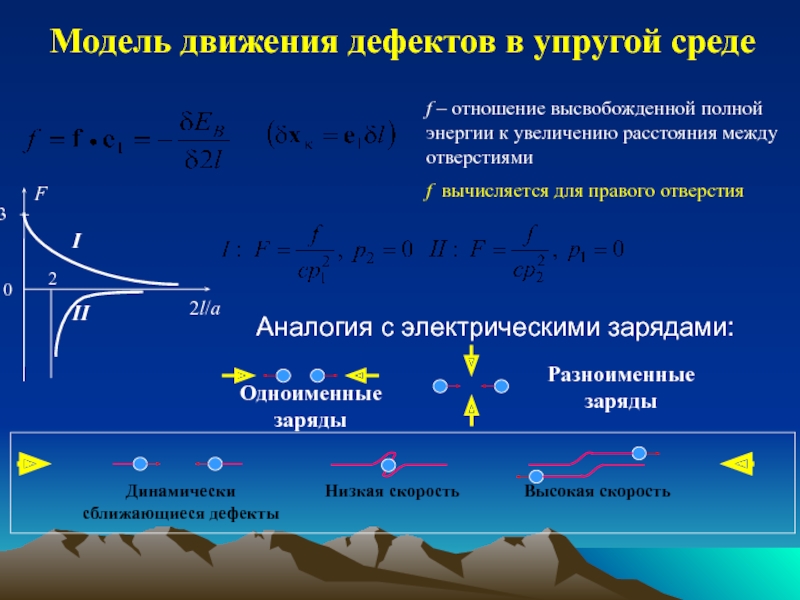
обзор индикаторов и методов определения напряжений;
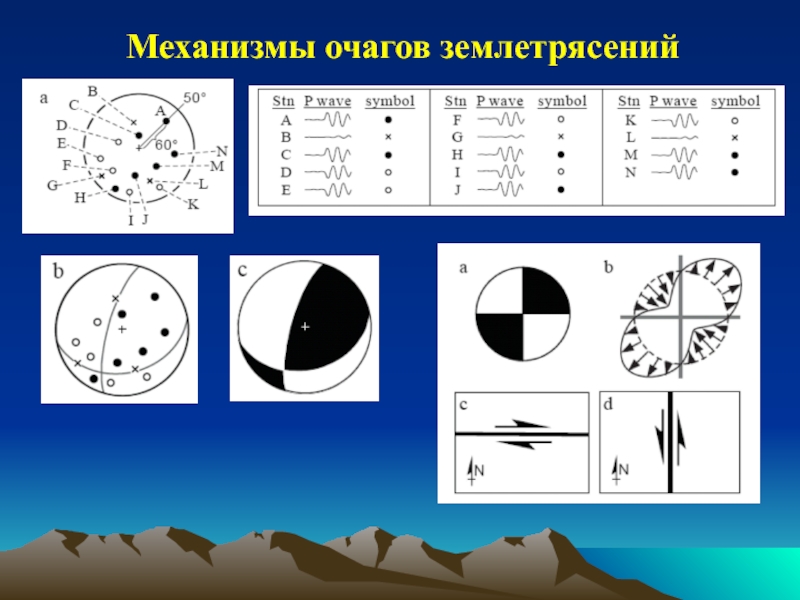
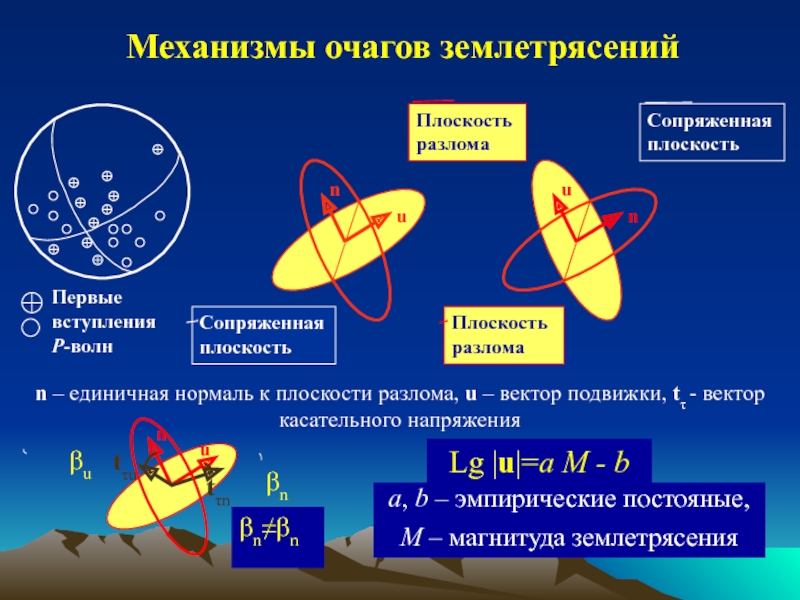
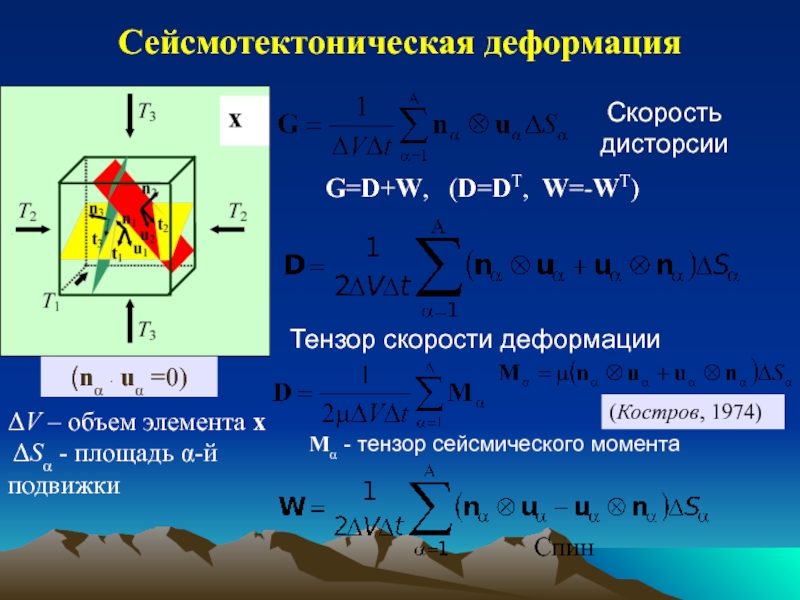
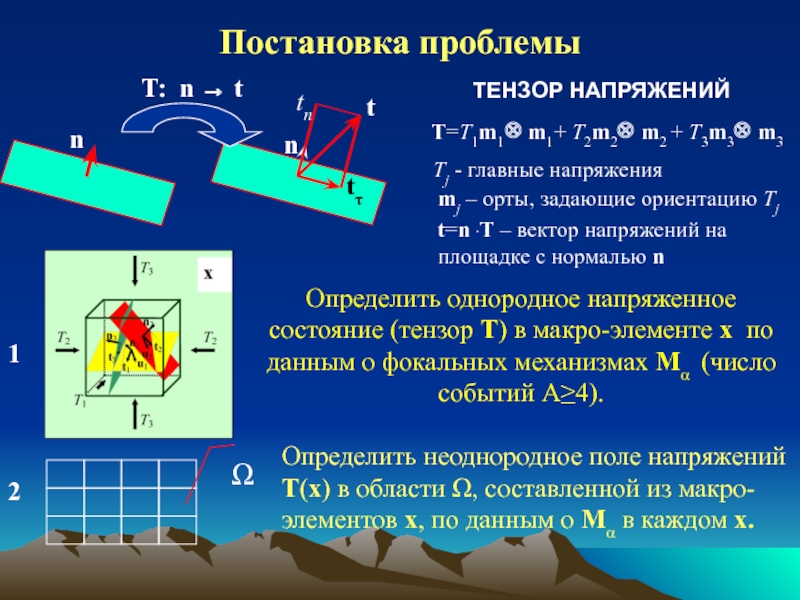
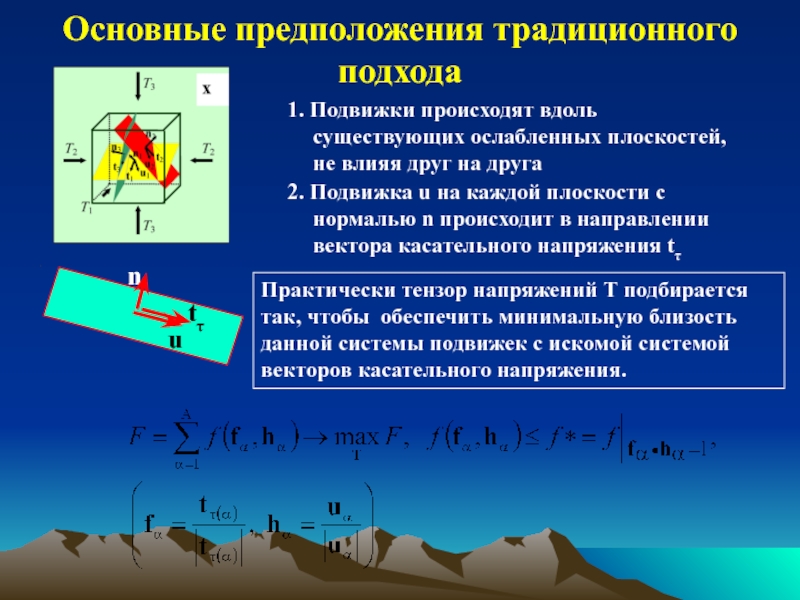
Определение напряжений по механизмам
землетрясений; Определение палеонапряжений по трещиноватости осадочных горных пород
Ш.А. Мухамедиев