Мухамедиев
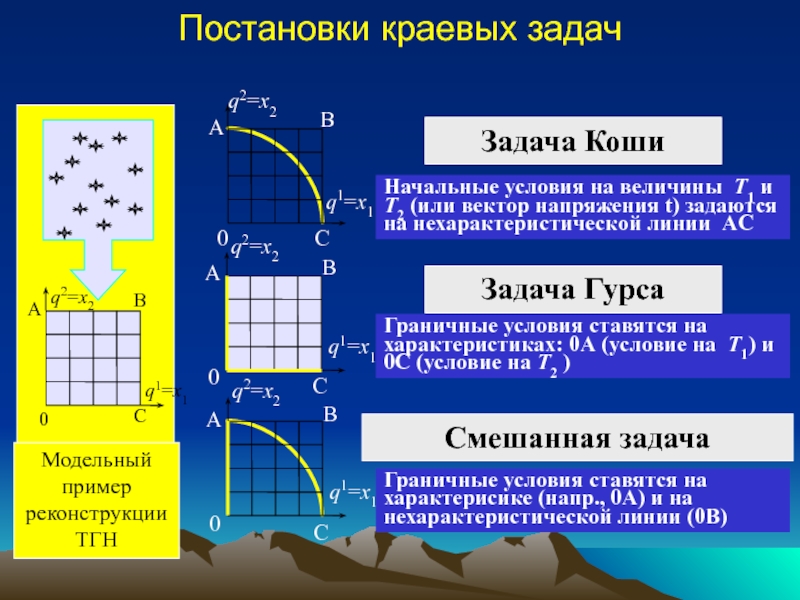
Уравнения равновесия в форме Ламе-Максвелла; гиперболичность системы уравнений равновесия при
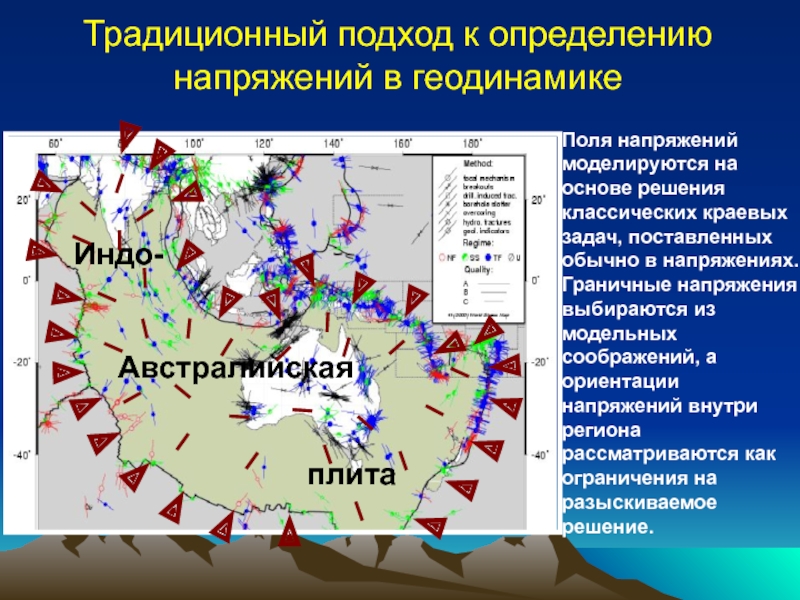
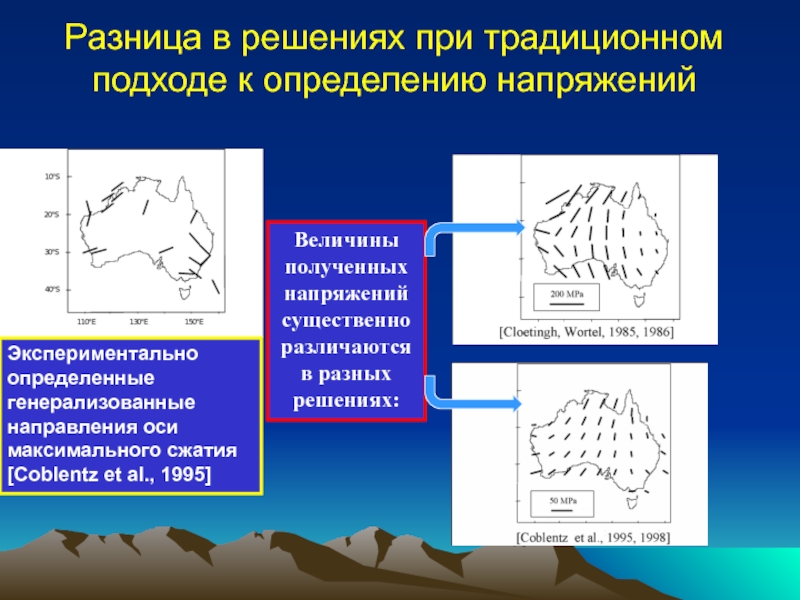
заданных ТГН;Определение полей напряжений по заданным ТГН в литосфере произвольной реологии;
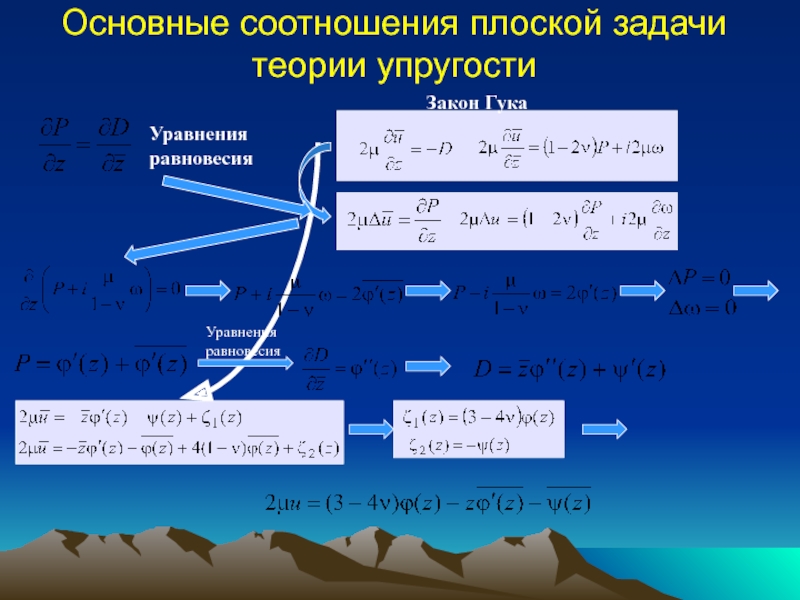
Плоская задача теории упругости, формулы Колосова-Мусхелишвили;
Определение голоморфной и биголоморфной функции по ее аргументу;
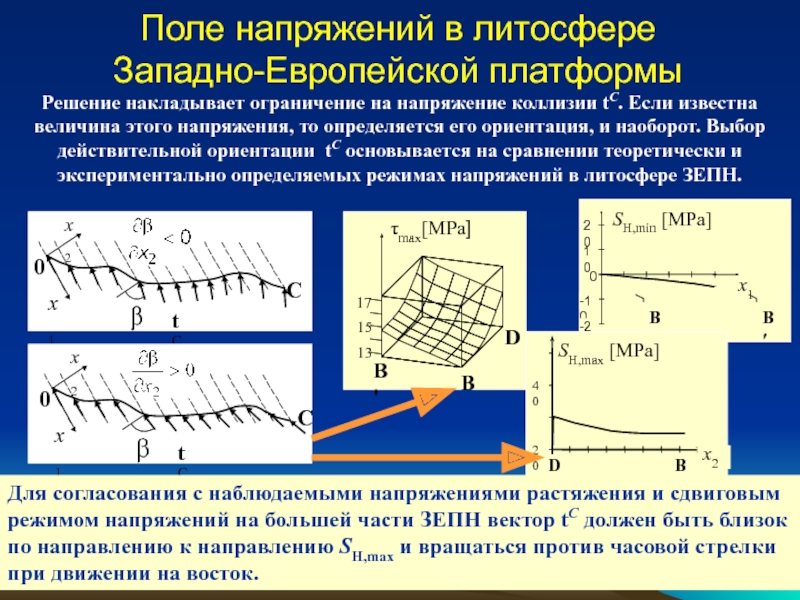
Определение полей напряжений по заданным ТГН в упругой литосфере.