ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

(1)

Приращение функции :

∆f = f(x0 +∆x)-f(x0) (2)

∆f = f(x)-f(x0) (3)

x

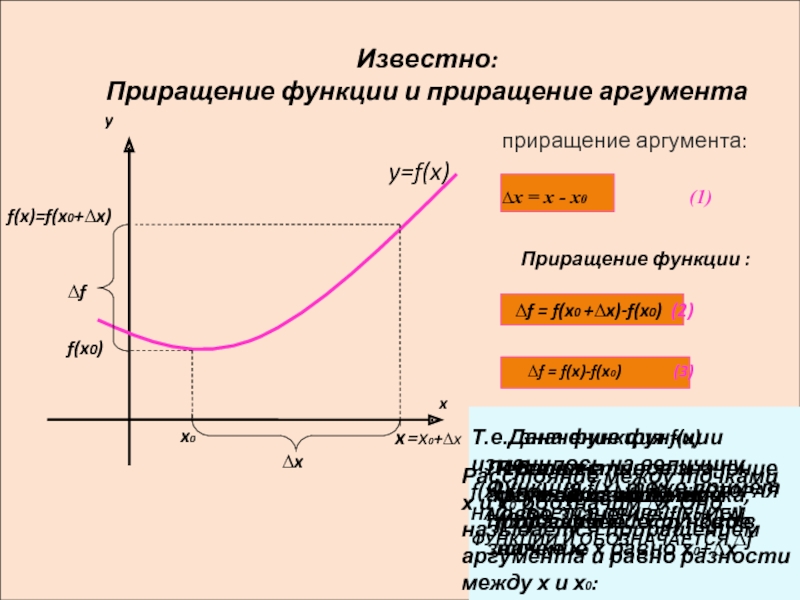
В окрестности точки х0 возьмём точку х

Пусть х0- фиксированная точка, f(х0)- значение функци в точке х0

Расстояние между точками х и х0 обозначим ∆х.Оно называется приращением аргумента и равно разности между х и х0:

Первоначальное значение аргумента получило приращение ∆х, и новое значение х равно х0+∆х

Функция f(х) тоже примет новое значение: f(x0+∆x)

Т.е., значение функции изменилось на величину f(x)-f(x0)= f(x0 +∆x)-f(x0),КОТОРАЯ НАЗЫВАЕТСЯ ПРИРАЩЕНИЕМ ФУНКЦИИ И ОБОЗНАЧАЕТСЯ ∆f

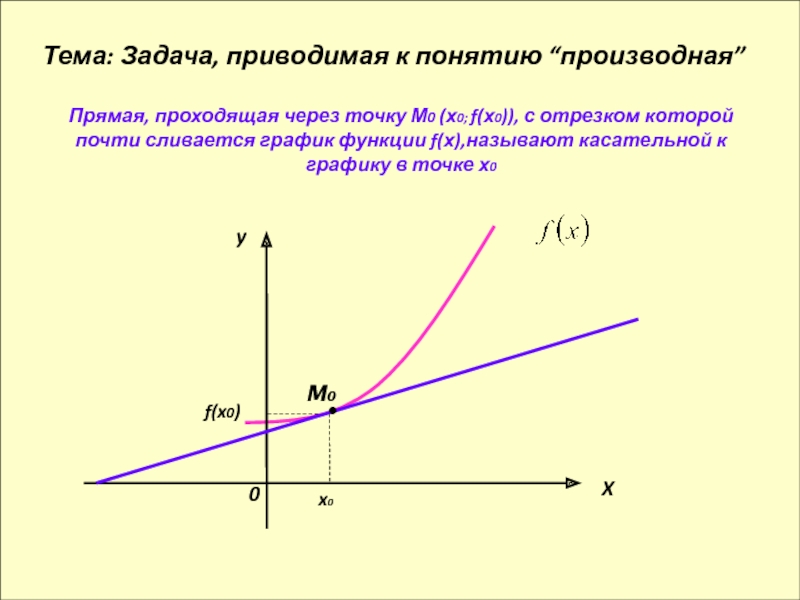
Дана функция f(x)

начало отсчета, единица измерения (метр) и направление, движется некоторое тело

(материальная точка).
Закон движения задан формулой s=s (t), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах).
Найти скорость движения тела в момент времени t (в м/с).

М
пройдя путь от начала движения ОМ = s(t). Дадим

аргументу t
приращение ∆t и рассмотрим момент времени t+∆t Координата
материальной точки стала другой, тело в этот момент будет
находиться в точке P : OP=s(t+∆t) Значит, за ∆t секунд тело переместилось из точки М в точку Р, т.е. прошло путь МР. Имеем:
MP=OP-OM=s(t+∆t)-s(t)=∆s Полученную разность мы назвали приращением функции
Путь ∆s тело прошло за ∆t секунд.
Нетрудно найти среднюю скорость движения тела за промежуток времени [t; t+∆t] :
=

А что такое скорость v (t) в момент времени t (ее называют иногда
мгновенной скоростью)? Можно сказать так: это средняя скорость движения
за промежуток времени [t; t+∆t] при условии , что ∆t выбирается все меньше и
меньше; точнее: иными словами, при условии, что ∆t→0.Это значит , что

Подводя итог решению задачи 1, получаем:

Движение свободно падающего тела явно неравномерное. Скорость v постепенно возрастает.

Но как именно выглядит зависимость v(t) ?

v(t). Пусть h – небольшой промежуток времени, прошедший от момента

t. За это время падающее тело пройдёт путь, равный s(t+h)-s(t).
Если промежуток времени h очень мал, то приближённо
s(t+h)-s(t)≈v(t)∙h, или , причём

последнее приближённое равенство тем точнее, чем меньше h. Значит величину v(t) скорости в момент t можно рассматривать как предел, к которому стремится отношение, выражающее среднюю скорость на интервале времени от момента t до момента t+h.
Сказанное записывают в виде

почти сливается график функции f(х),называют касательной к графику в точке

х0

x0

f(x0)

M0

X

y

Тема: Задача, приводимая к понятию “производная”

0

к положению касательной
Предельным положением секущей МоМ,
когда М неограниченно приближается

к Мо, является касательная

Пусть дан график функции f(х) и касательная, проходящая через точку М0 ,которая образует с положительным направлением оси ОХ угол φ

Отметим точку М, координаты которой рассмотрим как приращение координат точки М0

Через точки М и М0 проведём секущую, которая образует с осью ОХ угол 

Будем перемещать точку М вдоль графика, приближая её к точке М0.Соответственно будет меняться положение секущей ММ0

При этом координата х точки М будет стремиться к х0

К чему будет стремиться приращение аргумента?

А к какому углу будет стремиться угол  ?

электричества, протекающее через поперечное сечение проводника за время t.
Пусть

Δt – некоторый промежуток времени, Δq = q(t+Δt) – q(t) – количество электричества, протекающее через указанное сечение за промежуток времени от момента t до момента t + Δt. Тогда отношение называют средней силой тока.
Мгновенной силой тока в момент времени t называется предел отношения приращения количества электричества Δq ко времени Δt, при условии, что Δt→0.

же математической модели – пределу отношения приращения функции к приращению

аргумента при условии, что приращение аргумента стремится к нулю. Значит, эту математическую модель надо специально изучить, т.е.:
Присвоить ей новый термин.
Ввести для неё обозначение.
Исследовать свойства новой модели.
Определить возможности применения нового понятия - производная

за промежуток времени [t0; t1] (масса соли, растворившейся в воде

изменяется по закону х = f(t) определяется по формуле:


Скорость растворения в данный момент
времени

приращения функции к приращению аргумента при последнем стремящимся к нулю:

движения есть производная от пути по времени;
б) угловой коэффициент касательной

к графику функции в точке (x0; f(x)) есть производная функции f(x) в точке х = х0;
в) мгновенная сила тока I(t) в момент t есть производная от количества электричества q(t) по времени;
Г) скорость химической реакции в данный момент времени t есть производная от количества вещества у(t), участвующего в реакции, по времени t.

∆x = x – x0
2)

∆f = f(x+x0) – f(x0)
3)

4)

задач из естественных и гуманитарных наук, экономических задач оптимизационного характера.

И, конечно, не обойтись без производной при исследовании функции и построении графиков, решении уравнений и неравенств

«…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И. Лобачевский

=
Мгновенная скорость
или
Скорость изменения функции

Значение производной в точке

=