Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
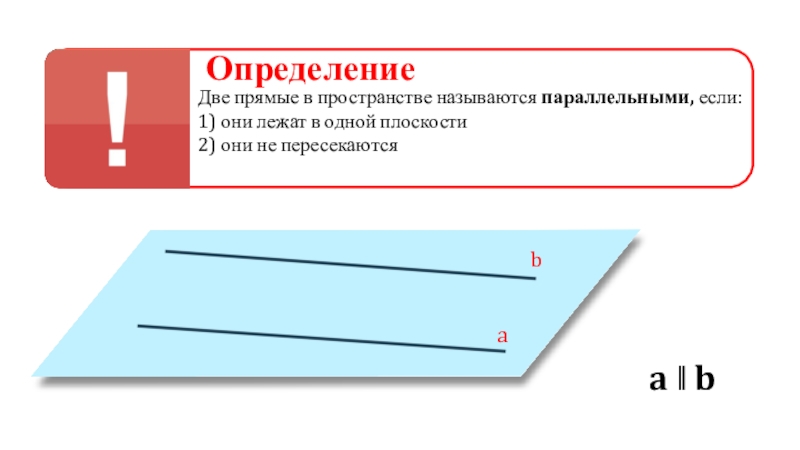
Определение Две прямые в пространстве называются параллельными, если: 1) они
Содержание
- 1. Определение Две прямые в пространстве называются параллельными, если: 1) они
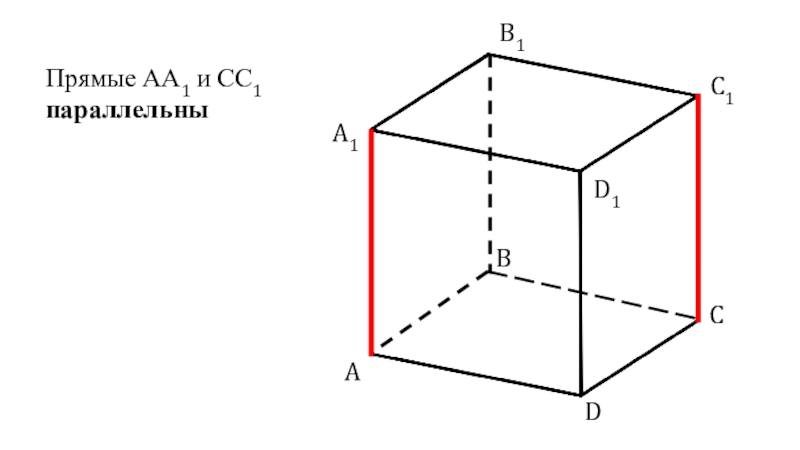
- 2. ABCDA1B1C1D1Прямые АА1 и СС1 параллельны
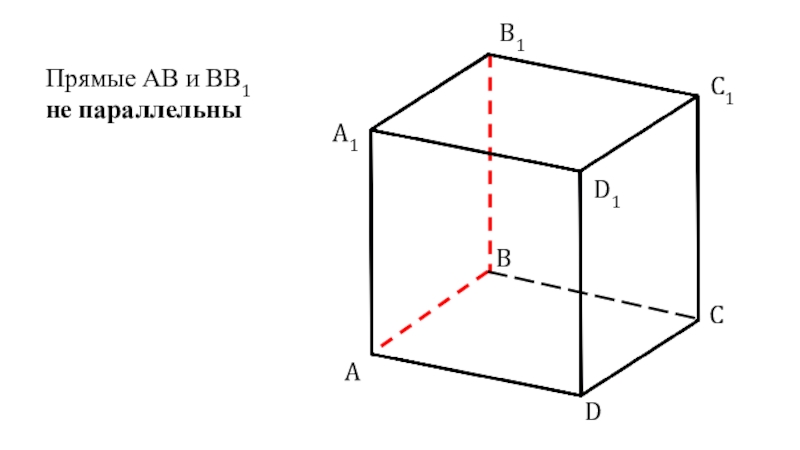
- 3. ABCDA1B1C1D1Прямые АВ и ВВ1 не параллельны
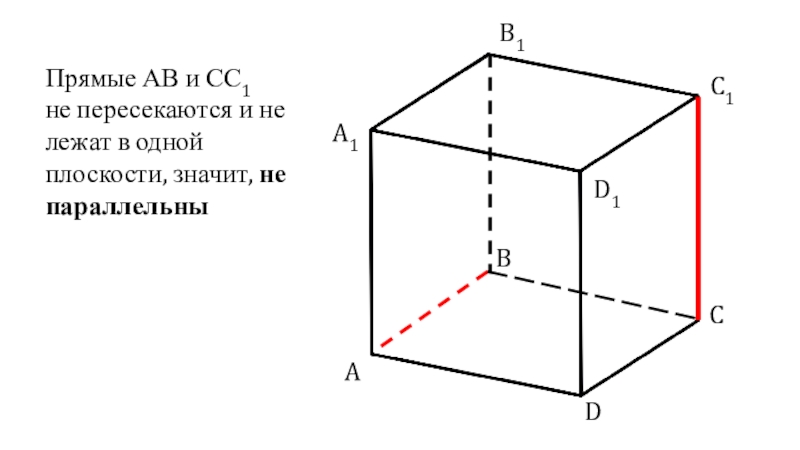
- 4. ABCDA1B1C1D1Прямые АВ и СС1 не пересекаются и не лежат в одной плоскости, значит, не параллельны
- 5. АксиомаЧерез точку, не лежащую на данной прямой, проходит только одна прямая, параллельная даннойabА
- 6. ТеоремаЧерез любую точку пространства, не лежащую на
- 7. ТеоремаЧерез любую точку пространства, не лежащую на
- 8. ОпределениеДва отрезка называются параллельными, если они лежат
- 9. Задачаа ∈ α , b ∈ α,
- 10. Скачать презентанцию
ABCDA1B1C1D1Прямые АА1 и СС1 параллельны
Слайды и текст этой презентации
Слайд 1Определение
Две прямые в пространстве называются параллельными, если:
1) они лежат
в одной плоскости
Слайд 4A
B
C
D
A1
B1
C1
D1
Прямые АВ и СС1
не пересекаются и не лежат в
одной плоскости, значит, не параллельны
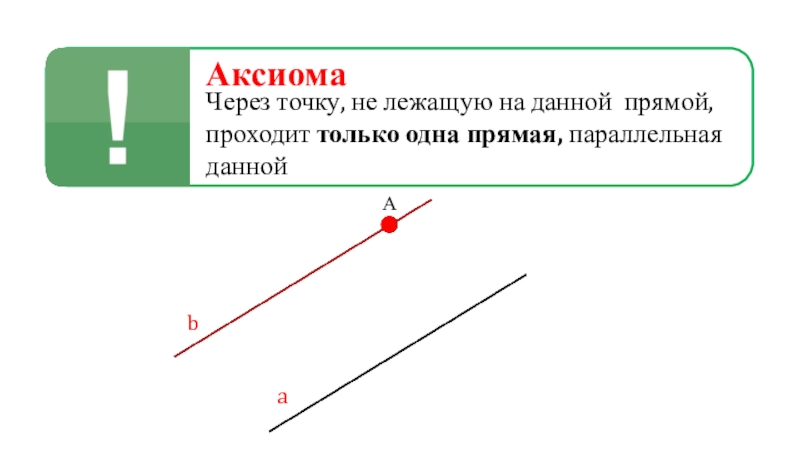
Слайд 5Аксиома
Через точку, не лежащую на данной прямой, проходит только одна
прямая, параллельная данной
a
b
А
Слайд 6Теорема
Через любую точку пространства,
не лежащую на данной прямой, проходит
прямая, параллельная данной, и притом только одна
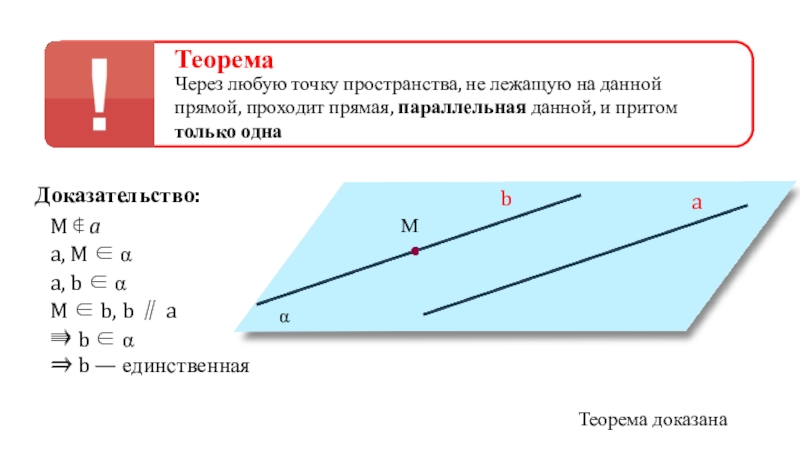
Слайд 7Теорема
Через любую точку пространства, не лежащую на данной прямой, проходит
прямая, параллельная данной, и притом только одна
Доказательство:
a
М
b
Теорема доказана
M ∉
a α
a, M ∈ α
a, b ∈ α
M ∈ b, b ∥ a ⇒
⇒ b ∈ α ⇒
⇒ b — единственная
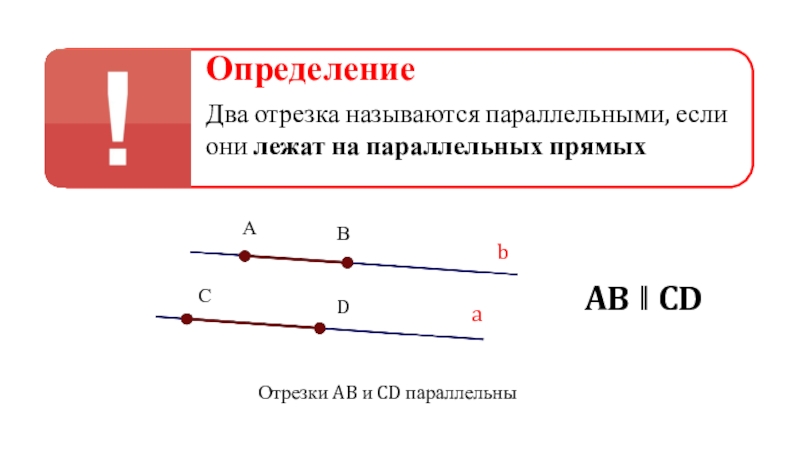
Слайд 8Определение
Два отрезка называются параллельными, если они лежат на параллельных прямых
a
b
AB ‖ CD
А
В
С
D
Отрезки AB и CD параллельны
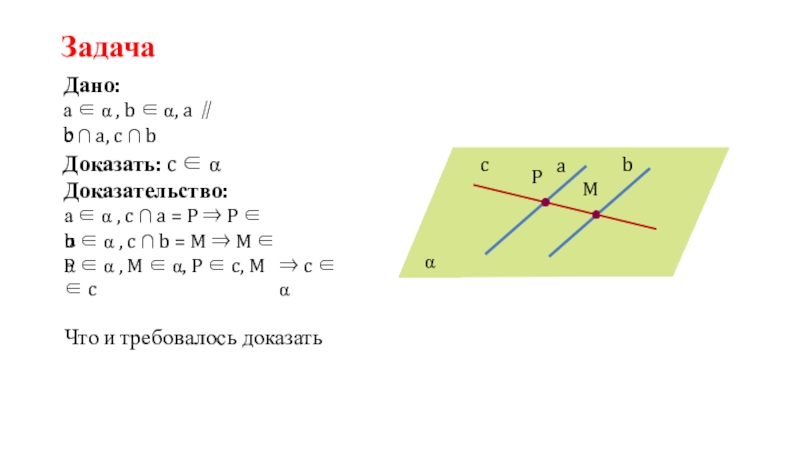
Слайд 9Задача
а ∈ α , b ∈ α, a ∥ b
Дано:
α
a
b
c ∩ a, c ∩ b
Доказать: c ∈ α
Доказательство:
а ∈
α , c ∩ a = P ⇒ P ∈ α b ∈ α , c ∩ b = M ⇒ M ∈ α
P ∈ α , M ∈ α, P ∈ c, M ∈ c
c
P
M
⇒ c ∈ α
Что и требовалось доказать