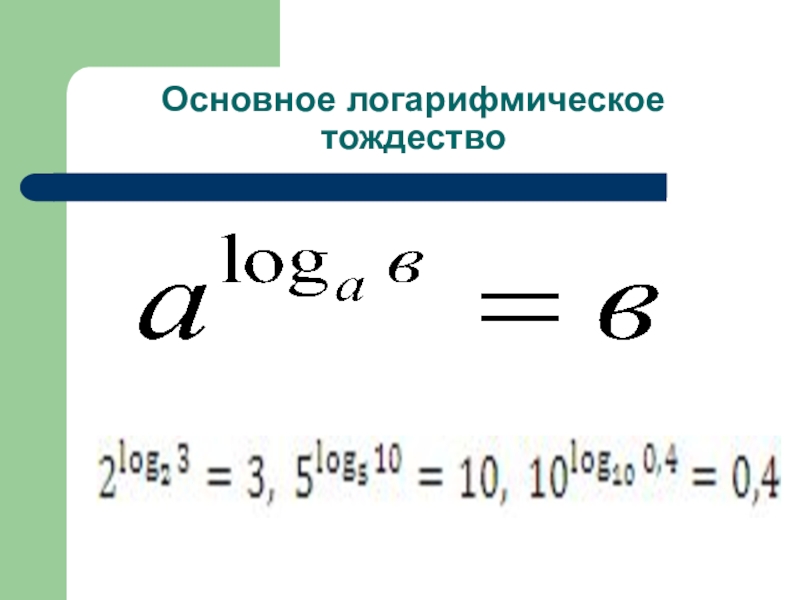Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определите тему урока, решив уравнения
Содержание
- 1. Определите тему урока, решив уравнения
- 2. Логарифм и его свойства
- 3. Джон Непер, изобретатель логарифмов В 1590
- 4. Логарифмическая линейкаВ настоящее время, с появлением компактных
- 5. Определение логарифмаЛогарифмом числа в>0 по основанию а>0
- 6. Логарифмическая спираль в природе Расположение семян на подсолнечникеРаковина наутилуса
- 7. Основное логарифмическое тождество
- 8. Свойства логарифмовloga 1 = 0.loga a = 1.loga xy =
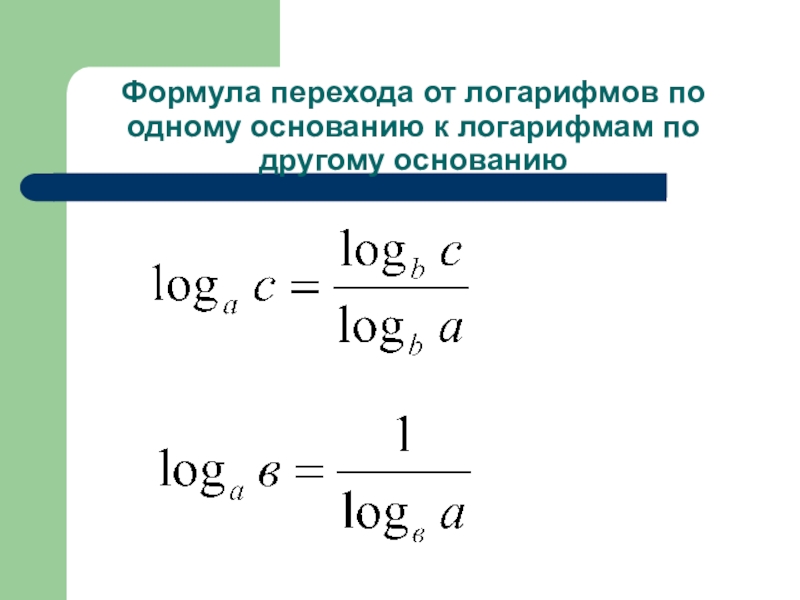
- 9. Формула перехода от логарифмов по одному основанию к логарифмам по другому основанию
- 10. Десятичные логарифмыЕсли основание логарифма равно 10, то логарифм называется десятичным:
- 11. Натуральные логарифмыЕсли основание логарифма е 2,7, то логарифм называется натуральным:
- 12. 1. Найдите логарифм числа 64 по основанию
- 13. 1. Вычислить: log612 + log63 Решение:log612 +log63
- 14. Вычислите
- 15. ДЗ в комментариях сообщества
- 16. Скачать презентанцию
Логарифм и его свойства
Слайды и текст этой презентации
Слайд 3Джон Непер,
изобретатель логарифмов
В 1590 году пришел к идее логарифмических
вычислений и составил первые таблицы логарифмов, опубликовал труд «Описание удивительных
таблиц логарифмов». В этом труде содержались определение логарифмов, объяснение их свойств. Изобрел логарифмическую линейку, счетный инструмент, использующий таблицы Непера для упрощения вычислений.Слайд 4Логарифмическая линейка
В настоящее время, с появлением компактных калькуляторов и компьютеров,
необходимость в использовании таблиц
логарифмов и логарифмических линеек отпала.
Слайд 5Определение логарифма
Логарифмом числа в>0 по основанию а>0 и а
1 называется показатель степени, в которую нужно возвести число
а, чтобы получить число в.- логарифм с произвольным основанием.
Например: а) log 3 81 = 4, так как 34 = 81; б) log 5 125 = 3, так как 53 = 125; в) log 0,5 16 = -4, так как (0,5)-4 = 16;
Слайд 8Свойства логарифмов
loga 1 = 0.
loga a = 1.
loga xy = loga x + loga y.
loga х
∕ у = loga x - loga y.
loga xp = p loga x
logaр x = 1 ∕
р loga xСлайд 12
1. Найдите логарифм числа 64 по основанию 4.
Решение: log464
= 3, так как 43 = 64.
Ответ: 3
2. Найдите число
x, если log5x = 2Решение: log5x = 2, x = 52 (по определению логарифма), x = 25.
Ответ: 25.
3. Вычислить: log31/ 81 = x,
Решение: log31/ 81 = x, 3x = 1/ 81, x = – 4.
Ответ: – 4.
Слайд 131. Вычислить: log612 + log63
Решение:
log612 +log63 = log6(12*3) =
log636 = log662 = 2
Ответ: 2.
2. Вычислить: log5250
– log52.Решение:
log5250 – log52 = log5(250/2) = log5125 = 3
Ответ: 3.
3. Вычислить:
Решение:
=
Ответ: 8.