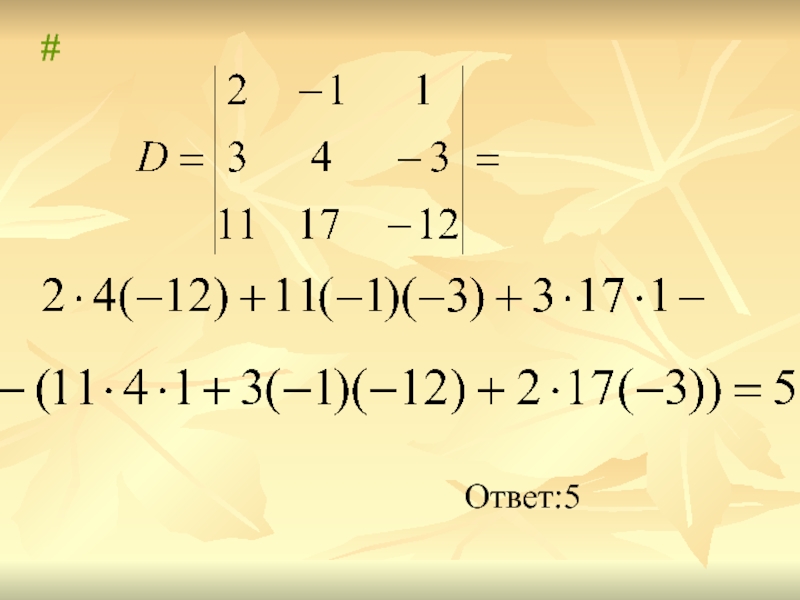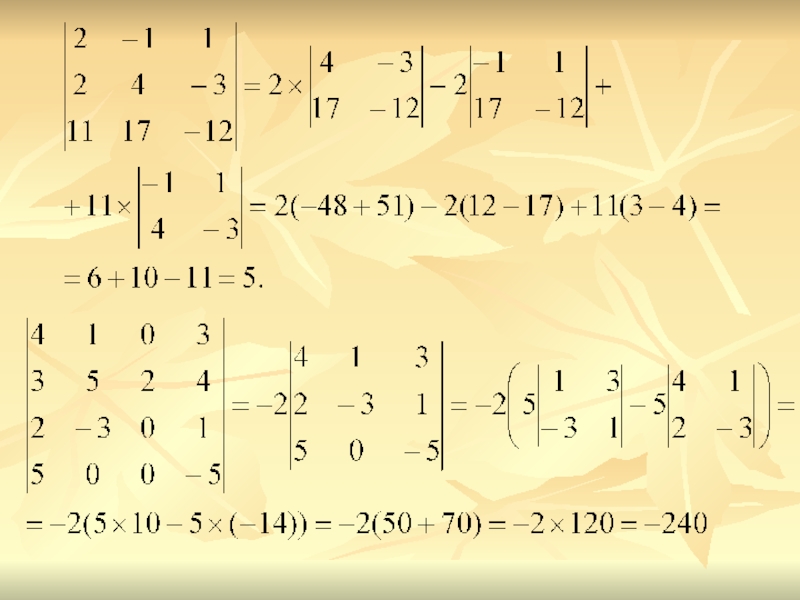Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определители. Решение систем методом Крамера
Содержание
- 1. Определители. Решение систем методом Крамера
- 2. Определители Правила вычисления
- 3. Слайд 3
- 4. #Ответ:5
- 5. Определитель n-го порядка.Записывается в виде квадратной таблицы,
- 6. Минор элемента аik Минором некоторого элемента aik
- 7. Алгебраическое дополнение Aik Алгебраическим дополнением элемента aik
- 8. Слайд 8
- 9. 2. Перестановка любых двух строк (столбцов) ,
- 10. 3. Общий множитель всех элементов одной строки
- 11. 6. Если к элементам одной строки (столбца)
- 12. Формулы КрамераЕсли определитель системы n линейных уравнений
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 5
Определитель n-го порядка.
Записывается в виде квадратной таблицы, содержащей
n2 элементов
вида a ik , расположенных в n строках
и n
столбцах:Слайд 6
Минор элемента аik
Минором некоторого элемента aik определителя n-го порядка
называется определитель n-1 –го, полученный из исходного путем вычеркивания строки
и столбца, на пересечении которых находится выбранный элемент и обозначается Мik.# a23=4
M23=
M31=5 M14=11
Слайд 7Алгебраическое дополнение Aik
Алгебраическим дополнением элемента aik данного D
называется Мik , взятый со знаком «+», если (i+k)- четное
число, и со знаком «-», если (i+k)- нечетное число.Для предыдущего примера:
А23=-М23=-13
А31=М31=5
А14=-М14=-11
Формула Лапласа.
Теорема: Определитель равен сумме произведений элементов всякой его строки (столбца) на их алгебраические дополнения.
Слайд 92. Перестановка любых двух строк (столбцов) , меняет только знак
D.
D’=-D
Свойства определителей.
1. Транспонирование определителя , т.е. замена строк столбцами и
наоборот, не меняет его значения. Слайд 103. Общий множитель всех элементов одной строки (столбца) м.б. вынесен
за знак D.
4. Если соответствующие элементы двух строк (столбцов)
равны или пропорциональны, то определитель равен 0.Слайд 116. Если к элементам одной строки (столбца) определителя прибавить соответственные
элементы другой строки или одинаковые пропорциональные им числа ,то исходный
определитель не изменится.5. Если элементы какой-либо строки (столбца) состоят из двух слагаемых, то определитель равен сумме двух определителей, различающихся между собой только элементами одной строки (столбца), бывшими ранее отдельными слагаемыми.
Слайд 12Формулы Крамера
Если определитель системы n линейных уравнений с n неизвестными
D≠0, то система совместна и имеет единственное решение, выражаемое по
следующим формулам:Dn – это определитель, который получается из определителя системы путем замены только n-го столбца столбцом свободных коэффициентов системы.