Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимальное планирование
Содержание
- 1. Оптимальное планирование
- 2. ЗадачаШкольный кондитерский цех готовит пирожки и пирожные.
- 3. Математическая модельПлановые показатели:X – дневной план выпуска
- 4. Получим соотношения, следующие из условия задачиX +
- 5. Получить оптимальный план, т.е. решить математическую задачу:
- 6. Криворотова Л.Н., МОУ "Гимназия", г.Тырныауз КБРСистема неравенств
- 7. Использование MS Excel для решения задачи оптимального планирования
- 8. Нахождение точки в которой целевая функция максимальна
- 9. Подготовить электронную таблицуРис.2. Таблица, подготовленная к вычислению оптимального плана
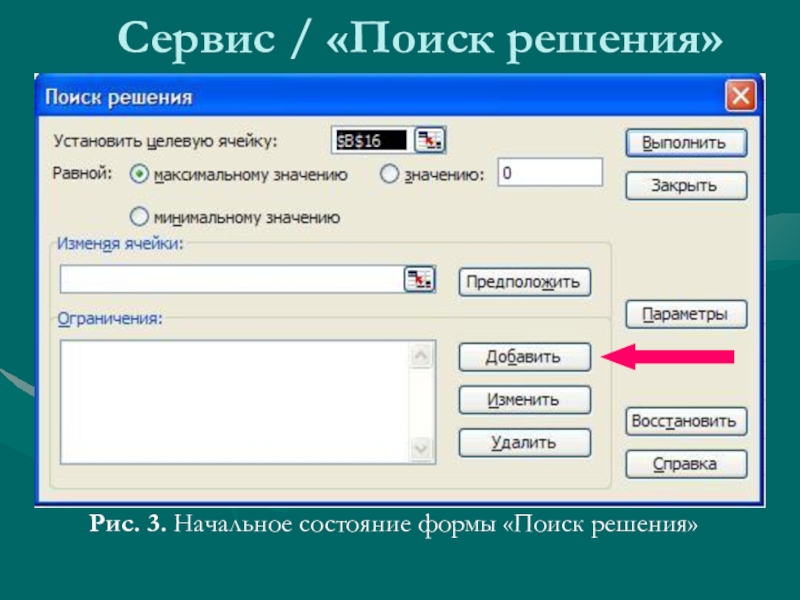
- 10. Сервис / «Поиск решения»Рис. 3. Начальное состояние формы «Поиск решения»
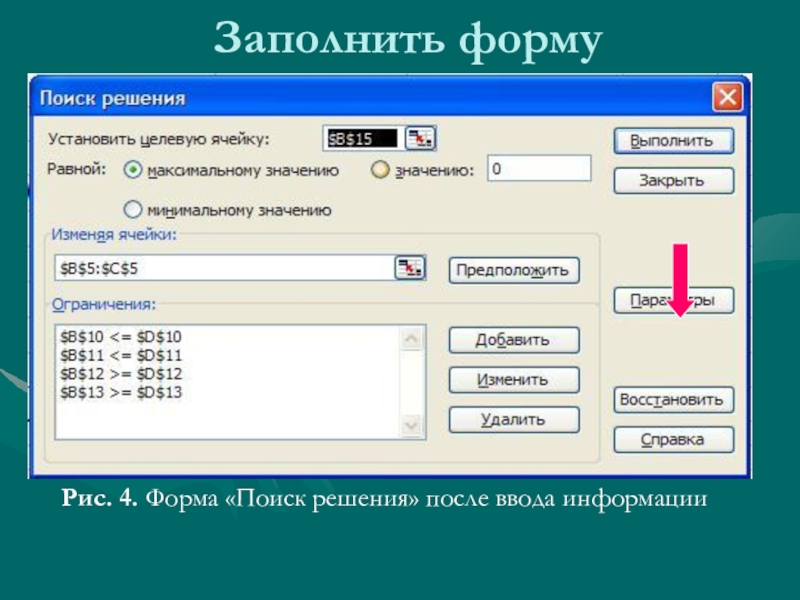
- 11. Заполнить формуРис. 4. Форма «Поиск решения» после ввода информации
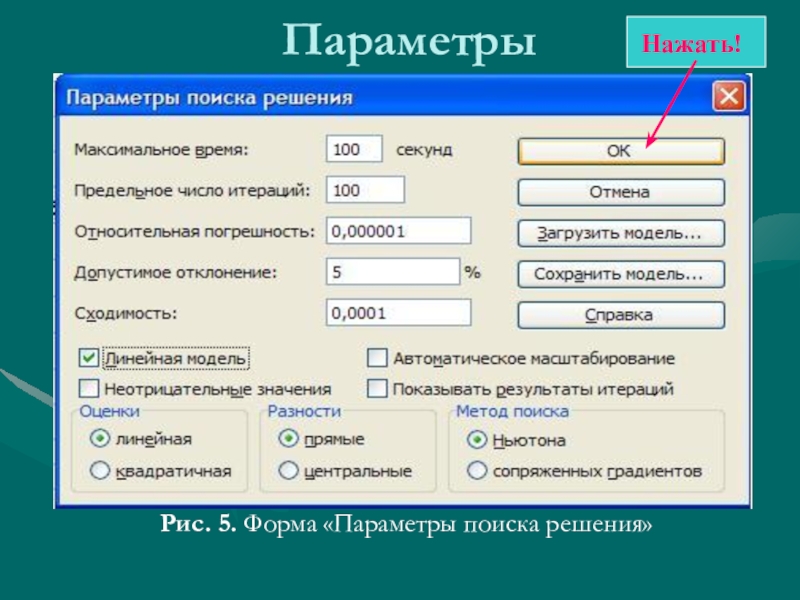
- 12. ПараметрыРис. 5. Форма «Параметры поиска решения»Нажать!
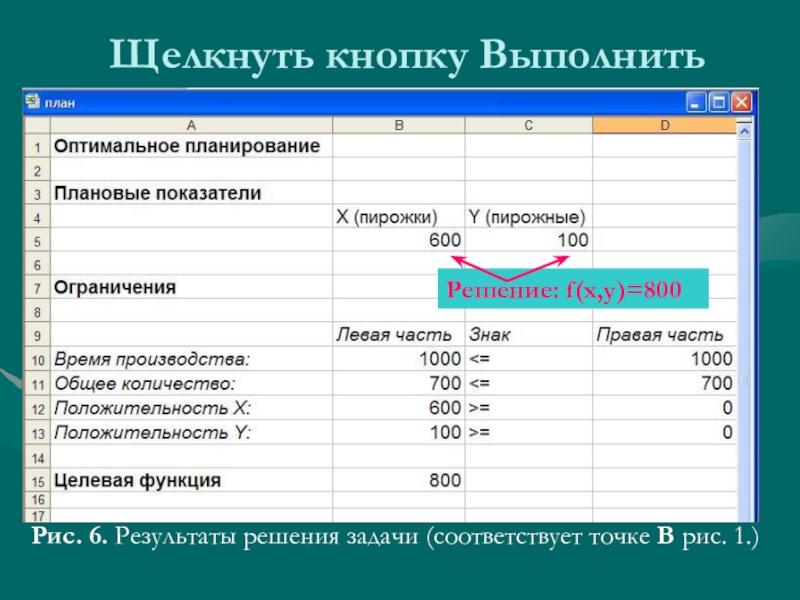
- 13. Щелкнуть кнопку ВыполнитьРис. 6. Результаты решения задачи (соответствует точке В рис. 1.)Решение: f(x,y)=800
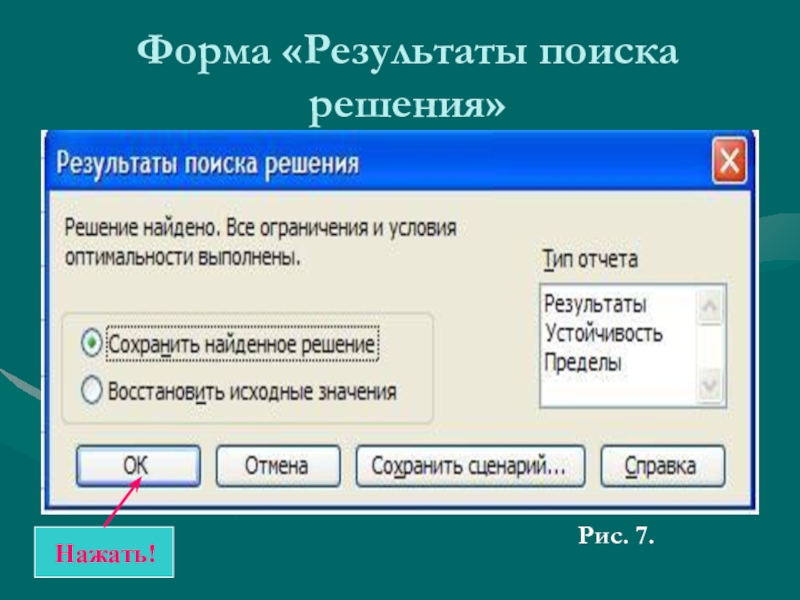
- 14. Форма «Результаты поиска решения»Рис. 7.Нажать!
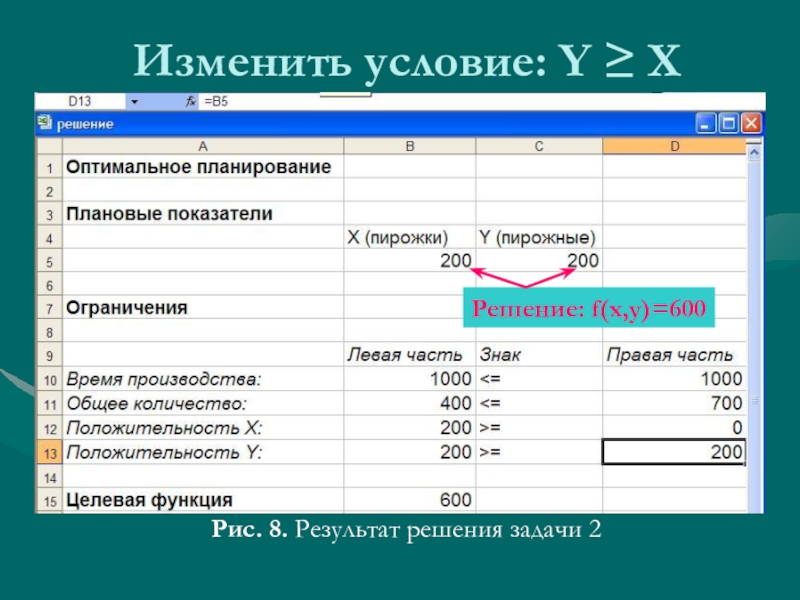
- 15. Изменить условие: Y ≥ XРис. 8. Результат решения задачи 2Решение: f(x,y)=600
- 16. При решении подобных задач могут
- 17. Контрольные вопросыКаково назначение программы-надстройки "Поиск решения"? Какова
- 18. Скачать презентанцию
ЗадачаШкольный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день в кондитерском цехе длится 8 часов. Если
Слайды и текст этой презентации
Слайд 3Математическая модель
Плановые показатели:
X – дневной план выпуска пирожков;
Y – дневной
план выпуска пирожных.
Ресурсы производства:
длительность рабочего дня – 8 часов;
вместимость
складского помещения - 700 мест.Слайд 4Получим соотношения, следующие из условия задачи
X + 4Y ≤ 1000;
X
+ Y ≤ 700;
X ≥ 0;
Y ≥ 0.
Перейдем к формализации
стратегической цели: получению максимальной выручки. Составим целевую функцию:
F(x, y) = r (x + 2y)
где r – цена одного пирожка в рублях
Поскольку значение r - константа, то в качестве целевой функции можно принять
F(x, y) = (x + 2y) (β)
(α)
Слайд 5Получить оптимальный план, т.е. решить математическую задачу: найти значения плановых
показателей X и Y, удовлетворяющих системе неравенств (α), при которых
целевая функция (β) принимает максимальное значение.Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием.
А поскольку в целевую функцию f (x,y) величины X и Y входят линейно (то есть в первой степени), то наша задача относится к разделу этой науки, который называется линейным программированием.
Слайд 6Криворотова Л.Н., МОУ "Гимназия", г.Тырныауз КБР
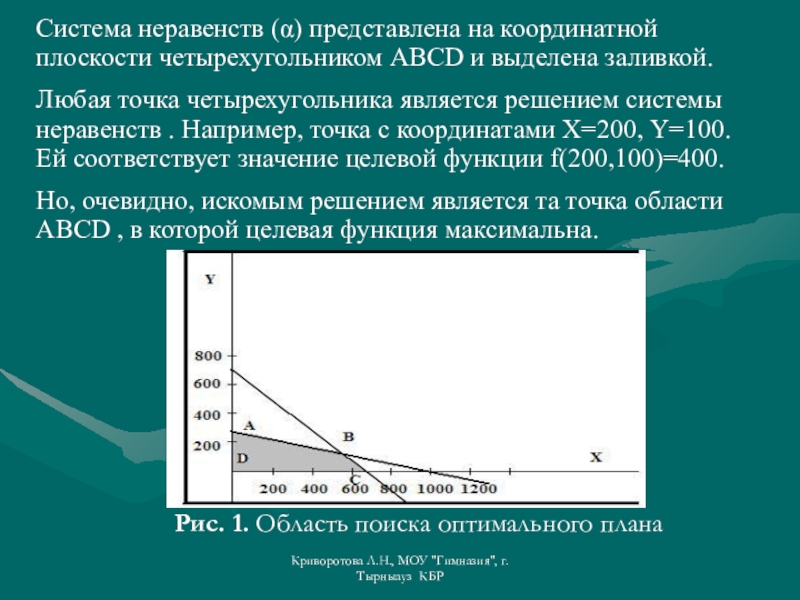
Система неравенств (α) представлена на
координатной плоскости четырехугольником ABCD и выделена заливкой.
Любая точка четырехугольника является
решением системы неравенств . Например, точка с координатами Х=200, Y=100. Ей соответствует значение целевой функции f(200,100)=400.Но, очевидно, искомым решением является та точка области ABCD , в которой целевая функция максимальна.
Рис. 1. Область поиска оптимального плана
Слайд 8Нахождение точки в которой целевая функция максимальна производится с помощью
методов линейного программирования. Эти методы имеются в математическом арсенале MS
Excel.Осуществляется это с помощью средства «Поиск решения». Команда находится в меню Сервис.
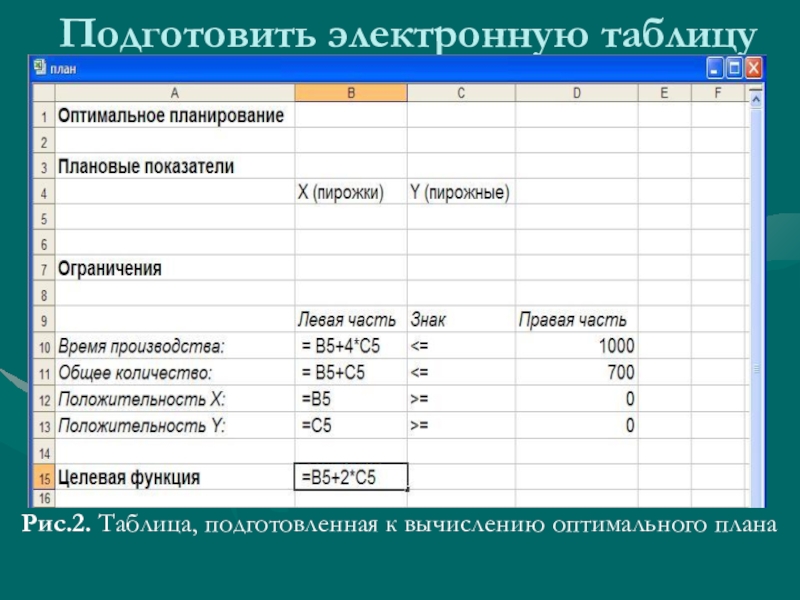
Слайд 9Подготовить электронную таблицу
Рис.2. Таблица, подготовленная к вычислению оптимального плана
Слайд 13Щелкнуть кнопку Выполнить
Рис. 6. Результаты решения задачи (соответствует точке В
рис. 1.)
Решение: f(x,y)=800
Слайд 16 При решении подобных задач могут возникнуть проблемы. Например,
искомого оптимального решения может вовсе не существовать – тогда программа
сообщит об этом.Слайд 17Контрольные вопросы
Каково назначение программы-надстройки "Поиск решения"?
Какова общая формулировка задачи
линейного программирования?
В чем заключается экономический смысл задачи линейного программирования?
Как будет сформулирована задача линейного программирования для рассматриваемого примера задачи об изготовлении пмрожков?
Как оформить в виде таблицы, отражающей основные зависимости, математическую формулировку задачи линейного программирования?
Каков смысл ячеек таблицы, подготовленной для поиска решения?
Как загрузить программу поиска решения задачи линейного программирования?
Какие параметры следует установить в окне "Поиск решения"?
Как интерпретировать полученные результаты решения задачи линейного программирования?