Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Оптимизация производственных процессов с помощью метода линейного
Содержание
- 1. Оптимизация производственных процессов с помощью метода линейного
- 2. Общие понятия оптимизацииМетоды оптимизации – методы, при
- 3. Линейное программирование — раздел математического программирования, изучающий
- 4. 2. Применение методов линейного программирования для оптимизации
- 5. Сформулируем ОЗЛП применительно к условиям задачи:требуется максимизировать
- 6. 2 этап. Базисные переменные х3, х4, х5,
- 7. Область допустимых решений (ОДЗ)6001203090150180301501201809060210240Х1Х2При х3=0 уравнение преобразуется
- 8. Область допустимых решений системы показана на рис.
- 9. 4 этап. Найдем решение, которое обеспечивает максимум
- 10. Решение ОЗЛП симплексным методомРассмотрим идею симплексного метода
- 11. 3. Находим первое базисное решение приравняв свободные
- 12. Проанализируем решение на оптимальность. Правило – если
- 13. Решение задачи оптимизации с применением офисных программ.
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Ограничения по с/х предприятию:
- 23. площадь сельскохозяйственных угодий — 4875 га, в
- 24. План продажи пшеницы, ц: >2700. ржи, ц:
- 25. Обозначения Площади посева (га): Х1 — озимая
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Оптимизация производственных процессов с помощью метода линейного программирования (ЛП)
Общие
понятия оптимизации
Слайд 2Общие понятия оптимизации
Методы оптимизации – методы, при реализации которых оптимальный
результат получается не сразу, а в результате процесса (оптимизации)
Решение
- определенный выбор зависящих от нас параметров процесса.Оптимальное решение – решение по каким-либо признакам предпочтительное, чем другие.
Элементы математической модели оптимизации:
Переменные – величины, оптимальные значения которых необходимо найти.
Параметры – постоянные величины, которые в процессе этого решения остаются неизменными и в модели представлены коэффициентами при переменных или свободными членами в уравнениях или неравенствах.
Критерий оптимальности – принятый показатель меры эффективности исследуемой системы (при экстремальном значении целевой функции определяет оптимальное решение для заданных условий).
Целевая функция – функция, которая связывает критерий оптимальности с переменными и параметрами. В процессе оптимизации определяется такие значения переменной величины, которые обращают значение целевой функции в максимум или минимум.
Ограничения – области возможных значений переменных оптимальных величин в данных условиях изучаемой системы, внутри которых отыскивается оптимальное решение.
Слайд 3Линейное программирование — раздел математического программирования, изучающий задачу отыскания максимума
(минимума) линейной функции при линейных ограничениях в виде равенств или
неравенств.Общая задача линейного программирования (ОЗЛП) формулируется:
требуется определить максимум (или минимум) линейной функции n переменных x1,x2,….., xn
при ограничениях:
где сj(j = l, 2, .... n), aij(i = 1, 2, ..., m; j = 1, 2, . .., n), bi (г = 1, 2, ..., m) — заданные числа.
Слайд 42. Применение методов линейного программирования для оптимизации процессов
Задача о
выборе парка сельскохозяйственных машин и объеме их производства.
Требуется определить,
в каком количестве следует производить сельхозмашины разных классов, чтобы обеспечить максимальную эффективность уборки урожая при заданных ресурсах. Имеются два вида машин K1 и K2. Обозначим через x1,x2 количество машин K1 и K2,
C1 и С2 — среднюю производительность машины,
b1, b2, b3, b4 — количество ограниченных ресурсов (стоимость, рабочая сила, дефицитные материалы и т. д.), которые отпускаются на производство сельскохозяйственных комплексов.
ai1 и ai2 —количество единиц i-го ресурса (i=l, 4), необходимое для производства одного комплекса первого и второго типа.
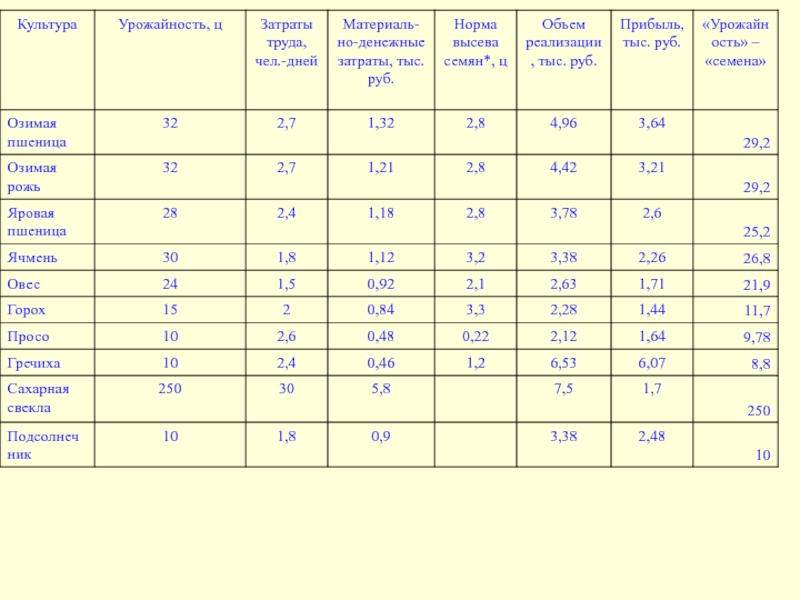
Значения для величин приведены в табл.
Слайд 5Сформулируем ОЗЛП применительно к условиям задачи:
требуется максимизировать линейную форму (целевая
функция) L=12x1 + 10x2 → max
Порядок решения ОЗЛП графическим
методом:1 этап. Для решения задачи, перейдем от неравенств к уравнениям.
Обозначим остаток неизрасходованных ресурсов первого типа х3, второго типа х4, третьего типа х5, четвертого типа х6, то получим исходное базисное решение
(1)
(2)
при следующих неравенствах:
Слайд 62 этап. Базисные переменные х3, х4, х5, х6 должны быть
положительны. Следовательно, систему уравнений (2) можно записать в виде неравенств
(3)3 этап. Найдем допустимую область возможных решений, удовлетворяющую этим неравенствам.
Для этого в прямоугольной системе координат построим прямые
Добавим к системе
два неравенства x1 >0, х2 > 0
(3)
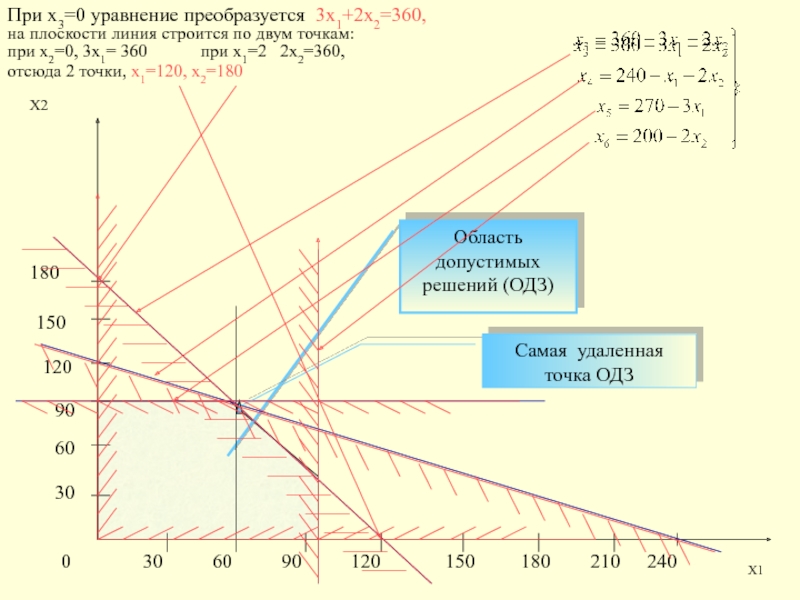
Слайд 7Область допустимых решений (ОДЗ)
60
0
120
30
90
150
180
30
150
120
180
90
60
210
240
Х1
Х2
При х3=0 уравнение преобразуется 3х1+2х2=360,
на плоскости
линия строится по двум точкам:
при х2=0, 3х1= 360
при х1=2 2х2=360, отсюда 2 точки, х1=120, х2=180
Самая удаленная точка ОДЗ
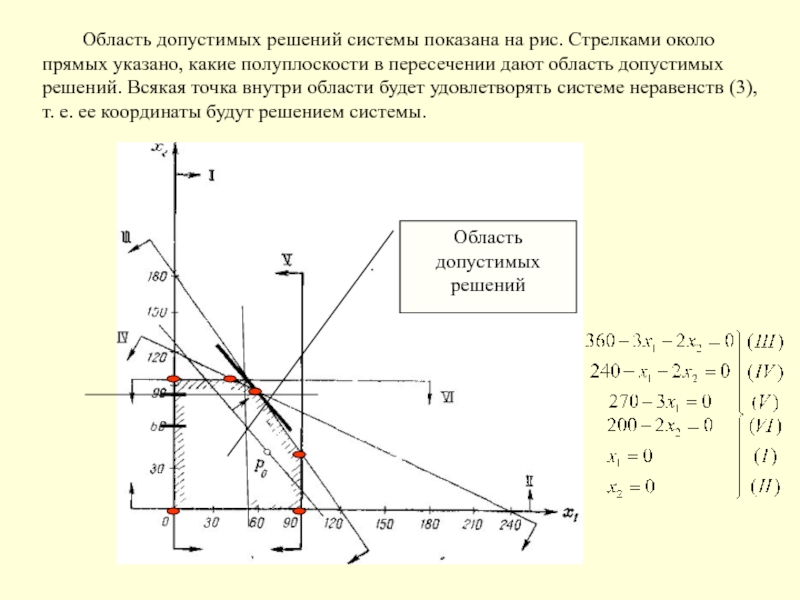
Слайд 8 Область допустимых решений системы показана на рис. Стрелками около прямых
указано, какие полуплоскости в пересечении дают область допустимых решений. Всякая
точка внутри области будет удовлетворять системе неравенств (3), т. е. ее координаты будут решением системы.Область допустимых решений
Слайд 9 4 этап. Найдем решение, которое обеспечивает максимум целевой функции.
А)
(см. учебник - М. П. Переверзев, С. И. Логвинов, С.
С. Логвинов Организация производства на предприятиях отрасли/ Курс лекций - Тула: ТГПУ им. Л.Н. Толстого, 2005 ) Возьмем в области допустимых решений любую точку, например Р0 (60, 50), которой соответствуют переменные Х1=60, Х2 = 50.Целевая функция в этом случае будет иметь значение
L=12x1 + 10x2 = 720 + 500 =1220.
Подставив это значение L в выражение ( ), получим уравнение прямой 12x1 + 10x2 =1220, или 12x1 + 10x2 — 1220 = 0. Любая точка этой прямой обеспечивает значение L=1220.
Перемещая полученную прямую параллельно самой себе в сторону увеличения L, находим оптимальное решение. Перемещение прекращается, когда все точки области решений неравенств останутся по одну сторону от этой прямой.
Б)Из рис. ясно, что оптимальному решению соответствует точка пересечения прямых III и IV, т е. одна из вершин многоугольника допустимых решений. Для определения координат этой вершины решим совместно уравнения прямых III и IV:
3x1 + 2x2 –360=0
x1 + 2x2 –240=0
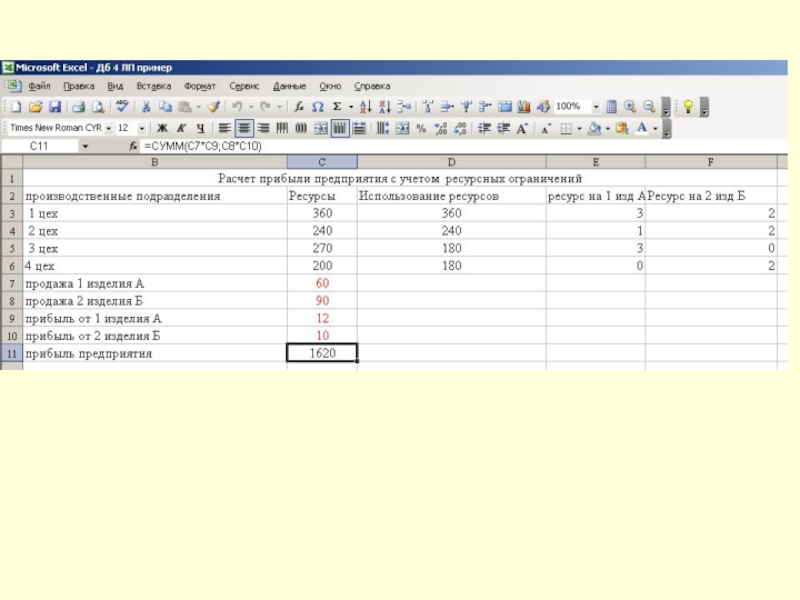
В результате решения получим x1 = 60; х2 = 90; х3=0; х4=0; х5 = 90; х6 = 20 и L = 1620.
Таким образом, необходимо выпускать 60 комплексов первого типа и 90 комплексов второго типа.
Анализ полученных решений показывает, что оптимальное решение всегда находится на границе допустимой области в одной из вершин многоугольника. На этом свойстве и основаны все методы линейного программирования.
Слайд 10Решение ОЗЛП симплексным методом
Рассмотрим идею симплексного метода на примере
Прибыль от
производства 2 изделий определяется целевой функцией:
П= Х1+2Х2 – максимум
При ограничениях
в трех цехах по ресурсам:Х1+Х2 ≤8
Х1≤6
Х2≤4
Х1,Х2≥0
Решение:
1. Приведем исходную задачу к ОЗЛП (за счет ввода новых дополнительных переменных переведем неравенства в равенства) – смотри геометрический метод.
Получим каноническую форму ОЗЛП:
Х1+Х2+Х3=8
Х1+Х4=6
Х2+Х5=4,
Где Х3…Х5 – искусственно введенные переменные (базисные)
2. Разрешаем систему относительно введенных дополнительных переменных
Х3=8 -Х1-Х2
Х4=6 -Х1
Х5=4- Х2
П= Х1+2Х2 – переменные в целевой функции называются свободными
Слайд 113. Находим первое базисное решение приравняв свободные переменные «0» Х1=Х2=0
Подставив
значения в целевую функцию и ограничения получим:
П=0, Х3=8, Х4=6, Х5=4
– т.е. это решение соответствует 0-точке на графике, или тому положению предприятия, когда оно не выпускает изделий и ресурсы не использованы ни в одном производственном подразделении.4. Определяем новое базисное решение.
Заменим свободную переменную в целевой функции на базисную (соответствует поиску решения по контуру графика – см.предыдущий пример).
Выберем для замены свободную переменную, которая быстрее увеличивает выбранный критерий (прибыль) – Х2, т.к. она имеет коэффициент 2
Для выбора заменяемой базисной переменной проанализируем систему уравнений на предыдущем шаге.
При изменении Х2 быстрее обращается в 0 переменная Х5 – при значении 4, т.к. Х3 при значении 8
Переведем Х2 в базисные, заменив ее на Х5, тогда
Х2=4- Х5
Х3=8 -Х1-(4- Х5) =4-Х1+Х5
Х4=6 -Х1
Целевая функция :
П=Х1+2(4- Х5)=Х1-2Х5+8
Базисное решение при этом при Х1=Х5=0 будет: П=8, Х2=4, Х3=4.
Это говорит о том, что ресурсы израсходованы полностью в третьем подразделении и частично в первом и втором. Выпуск изделий происходит только 2 типа (4 штуки). Прибыль предприятия – 8 единиц
Слайд 12Проанализируем решение на оптимальность.
Правило – если при анализе на
оптимальность целевой функции ее коэффициенты при свободных переменных отрицательны, то
она оптимальна, если есть положительны то необходимо продолжить поиск.Вывод: решение достигнутое на этом шагу (итерации) неоптимальное.
Определяем новое базисное решение (проводим очередную итерацию).
Заменяем свободную переменную с наибольшим положительным коэффициентом на выбранную базисную
Х1 на Х3, т.к. при анализе предыдущей системы уравнений на предыдущем шаге Х3 обращается при 4, а Х4 при 6.
Переводим в свободные переменные Х3
Х2=4- Х5
Х1=4- Х3+Х5
Х4=6 –(4- Х3+Х5)=2+Х3-Х5
Целевая функция:
П= Х1-Х5+8 = 4- Х3+Х5 –2Х5+8= 12-Х3-Х5
Вывод – целевая функция оптимальна, т.е. оптимальное решение достигнуто.
Находим параметры этого базисного решения приравняв свободные переменные
Х3 = Х5 =0.
Прибыль П= 12, количество выпушенной продукции при оптимальном плане Х1=4, Х2=4,
РесурсыХ3 иХ5 =0 – израсходованы полностью, Х4 – есть остаток ресурсов 2 единицы
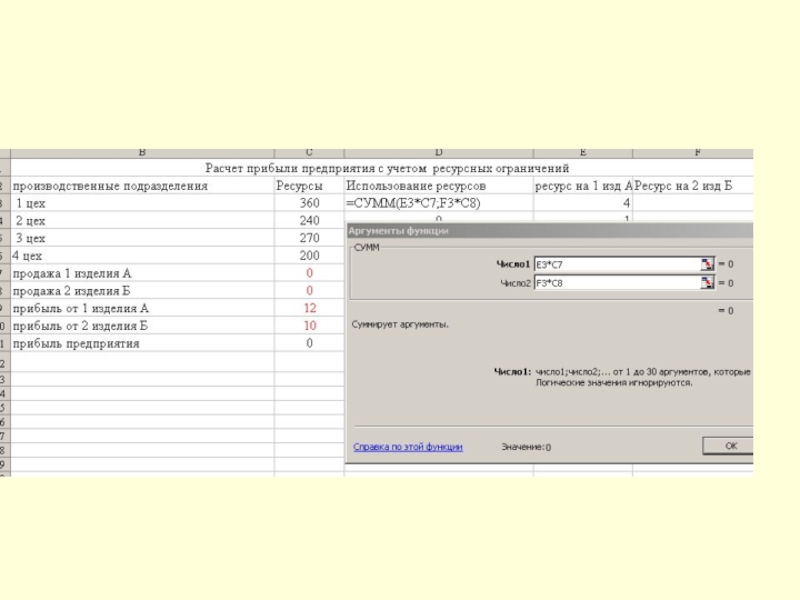
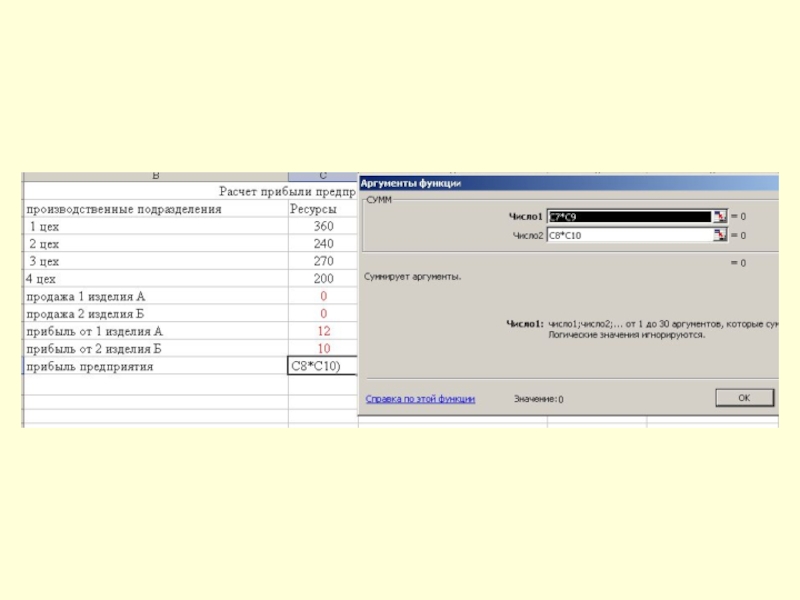
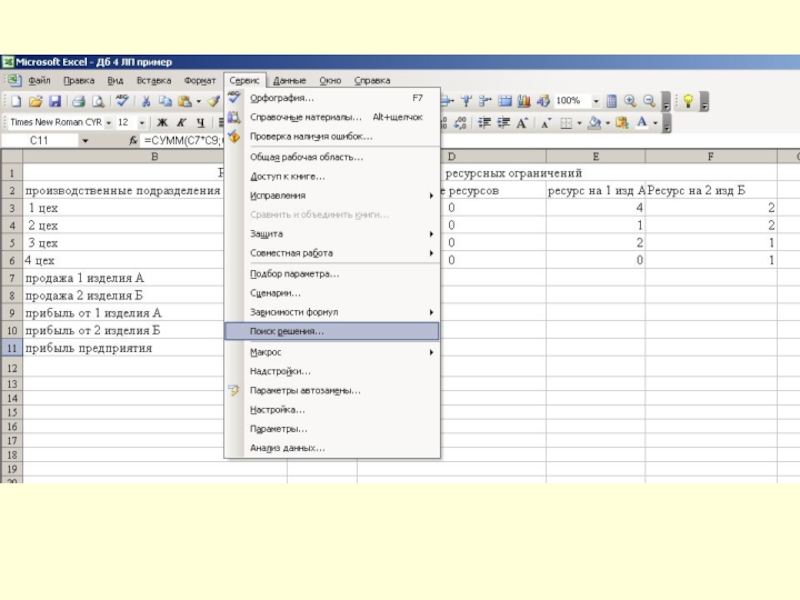
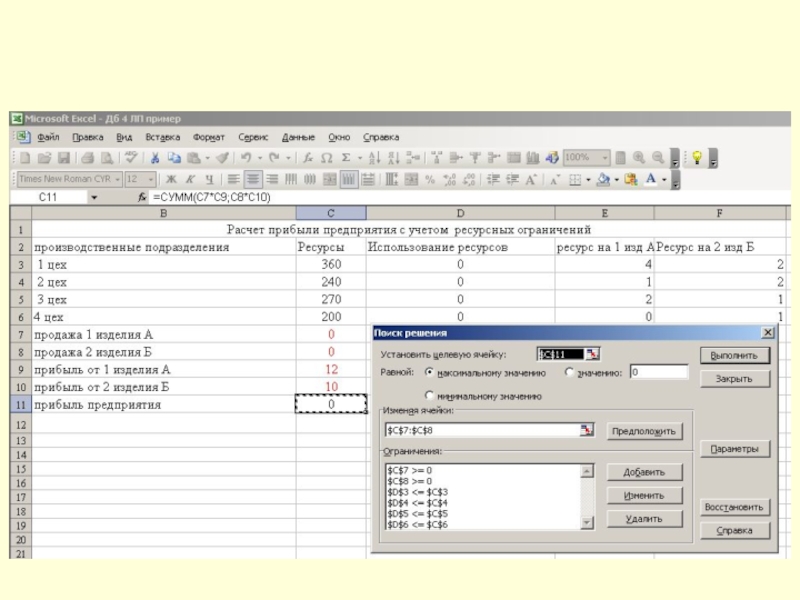
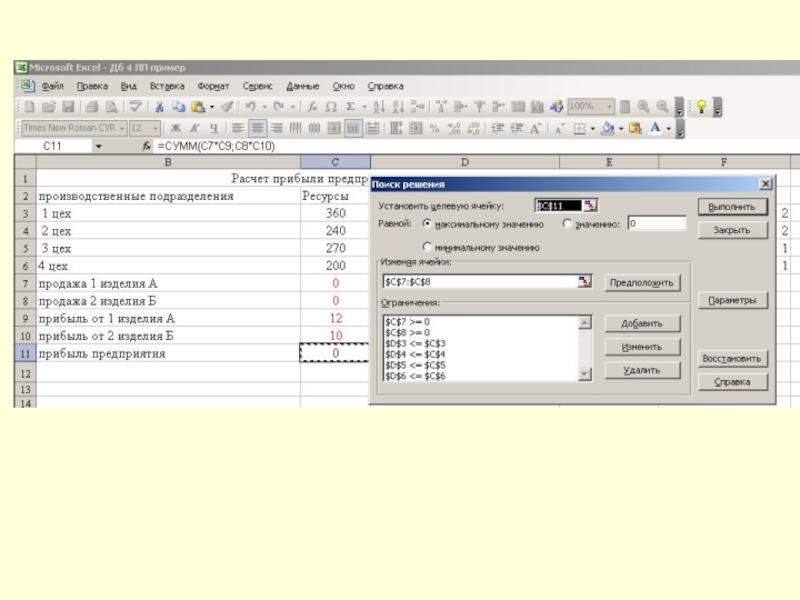
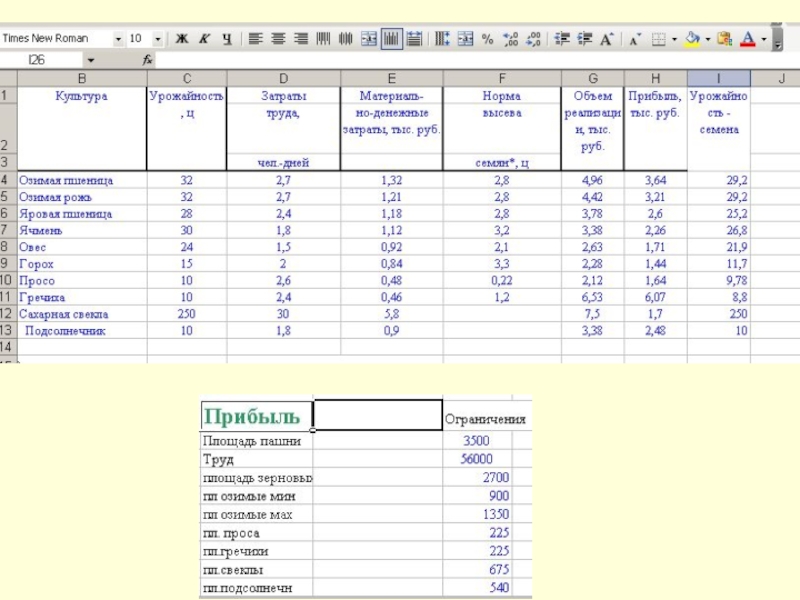
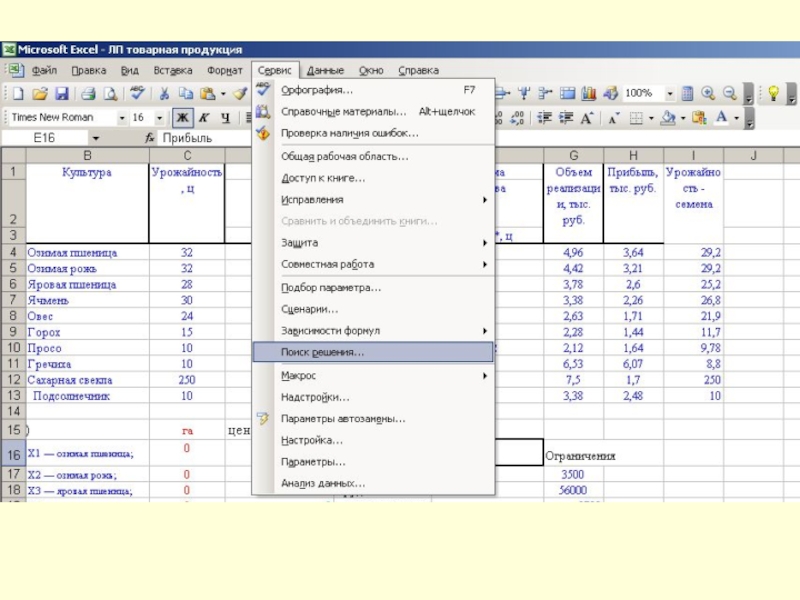
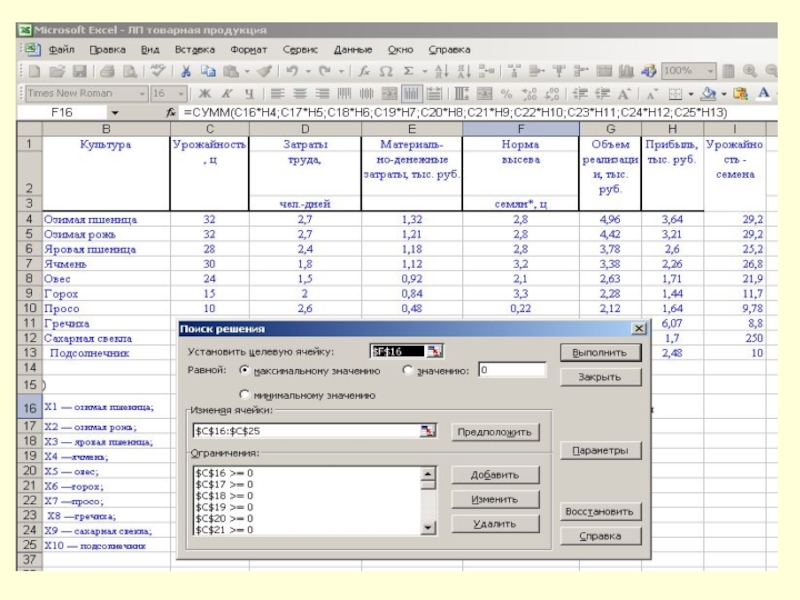
Слайд 13Решение задачи оптимизации с применением офисных программ.
1 этап –
введем исходные данные и формулы для расчета:
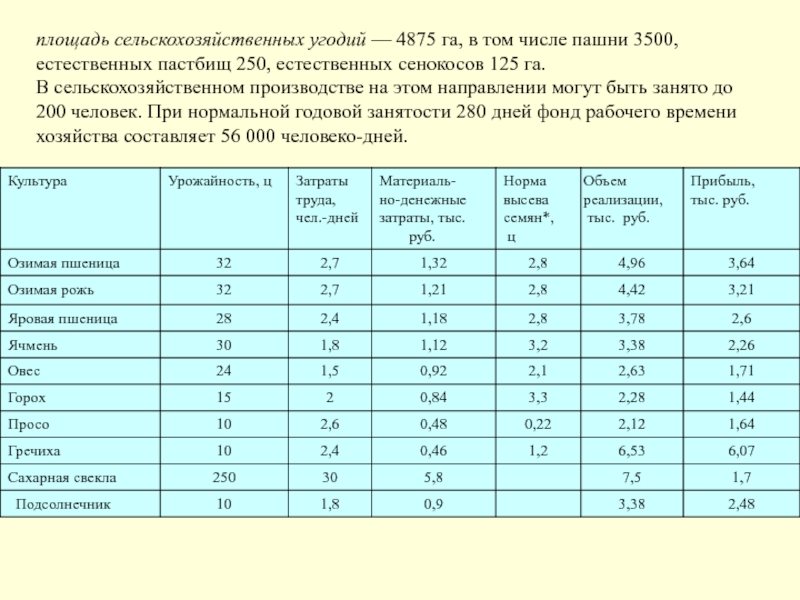
Слайд 23площадь сельскохозяйственных угодий — 4875 га, в том числе пашни
3500, естественных пастбищ 250, естественных сенокосов 125 га.
В сельскохозяйственном
производстве на этом направлении могут быть занято до 200 человек. При нормальной годовой занятости 280 дней фонд рабочего времени хозяйства составляет 56 000 человеко-дней.Слайд 24План продажи
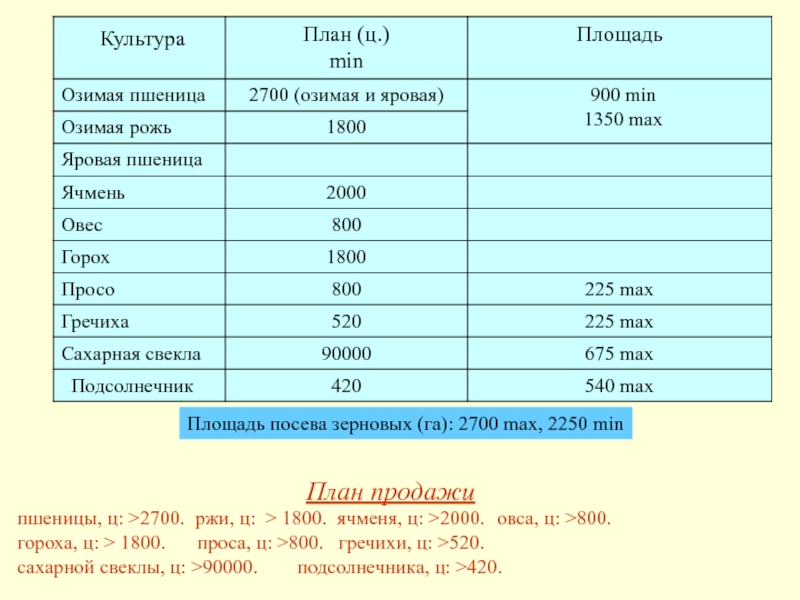
пшеницы, ц: >2700. ржи, ц: > 1800. ячменя,
ц: >2000. овса, ц: >800.
гороха, ц: > 1800.
проса, ц: >800. гречихи, ц: >520. сахарной свеклы, ц: >90000. подсолнечника, ц: >420.
Площадь посева зерновых (га): 2700 max, 2250 min
Слайд 25Обозначения Площади посева (га): Х1 — озимая пшеница; Х2 —
озимая рожь; Х3 — яровая пшеница; Х4 —ячмень; Х5 —
овес; Х6 —горох; Х7 —просо; Х8 —гречиха; Х9 — сахарная свекла; Х10 — подсолнечник.Ограничения:
Затраты труда, чел.-дней: 2,7X1 + 2,7Х2 + 2,4Х3 + 1,8Х4 + 1,5Х5 + 2Х6 + 2,6Х7 + 2,4Х8 + 30Х9 + 1,8Х10 + ≤ 56000.
Площадь пашни, га: X1 + Х2 + Х3 + Х4 + Х5 + Х6 + Х7 + Х8 + Х9 + Х10 < 3500.
Площадь посева зерновых, min (га): X1 + Х2 + Х3 + Х4 + Х5 + Х6 + Х7 + Х8 > 2250.
Площадь посева зерновых, max (га): X1 + Х2 + Х3 + Х4 + Х5 + Х6 + Х7 + Х8 ≤ 2700.
Озимые, min (га): Х1 + Х2>900.
Озимые, max (га): Х1 + Х2≤ 1350.
Площадь проса, max (га): Х7 ≤ 225.
Площадь гречихи, max (га) Х8 ≤ 225.
Площадь сахарной свеклы, max (га): Х9 ≤ 675.
Площадь подсолнечника, max (га): Х10≤ 540.
План продажи пшеницы, ц: 29,2Х1+ 25,2Х3>2700.
План продажи ржи, ц: 29,2Х2> 1800.
План продажи ячменя, ц: 26,8Х4>2000.
План продажи овса, ц: 21,9Х5>800.
План продажи гороха, ц 11,7Х6> 1800.
План продажи проса, ц: 9,8Х7>800.
План продажи гречихи, ц: 8,8Х8>520.
План продажи сахарной свеклы, ц: 250Х9>90000.
План продажи подсолнечника, ц: 10Х10>420.
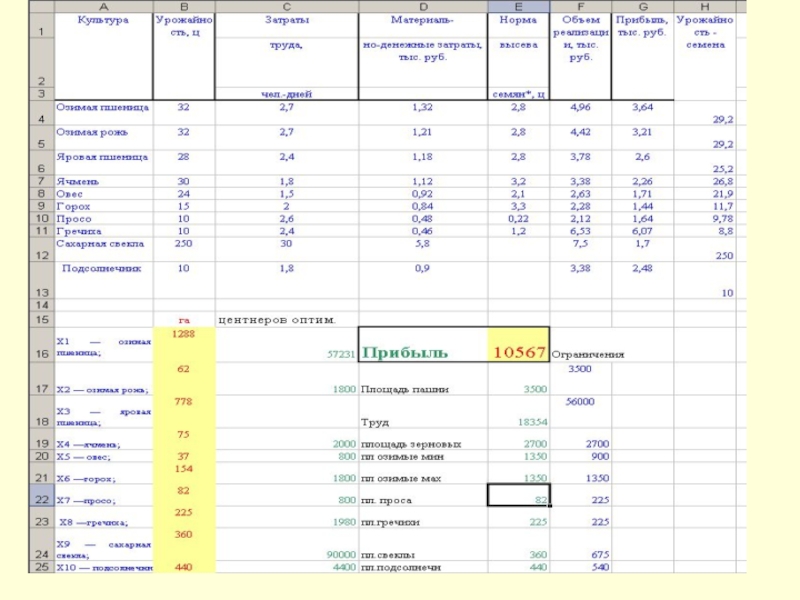
Целевая функция — максимум прибыли:
Z = 3,64X1 + 3,21Х2 + 2,6Х3 + 2,26Х4 + 1,71Х5 + 1,44Х6 + 1,64Х7 + 6,07Х8 + 1,7Х9 + 2,48Х10 -> max.