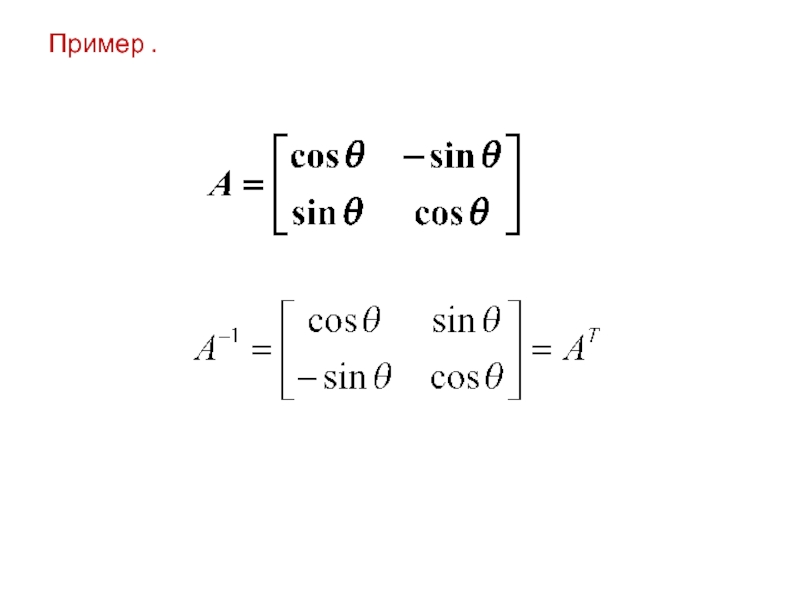= QT
называется ортогональной матрицей.
Следствие 1.2. Квадратная матрица Q ортогональна тогда
и только тогда, когдаQTQ = QQT = I.