Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные положения квантовой механики
Содержание
- 1. Основные положения квантовой механики
- 2. Квантовая механика - это физическая
- 3. Наука выявляет элементы объективной рельности
- 4. Существуют две интерпретации, или концепции,
- 5. Копенгагенская интерпретация квантовой механики Нильса
- 6. Если за частицей не ведется
- 7. Классическая материальная точка это маленький,
- 8. Этот ряд по большому счету
- 9. В микромире наблюдаемые физиками факты
- 10. Ситуация в квантовой механике выглядит
- 11. С точки зрения современных знаний
- 12. Мир, нас окружающий, и в
- 13. Большинство процессов в эволюционирующих системах необратимо.
- 14. Обыкновенная классическая механика - только
- 15. Типичные квантовые явления вполне аналогичны
- 16. Волновой дуализм де Бройля.
- 17. где λ - длина волны,
- 18. Оценим длину волны де Бройля
- 19. Необходимо также заметить, что аналогично
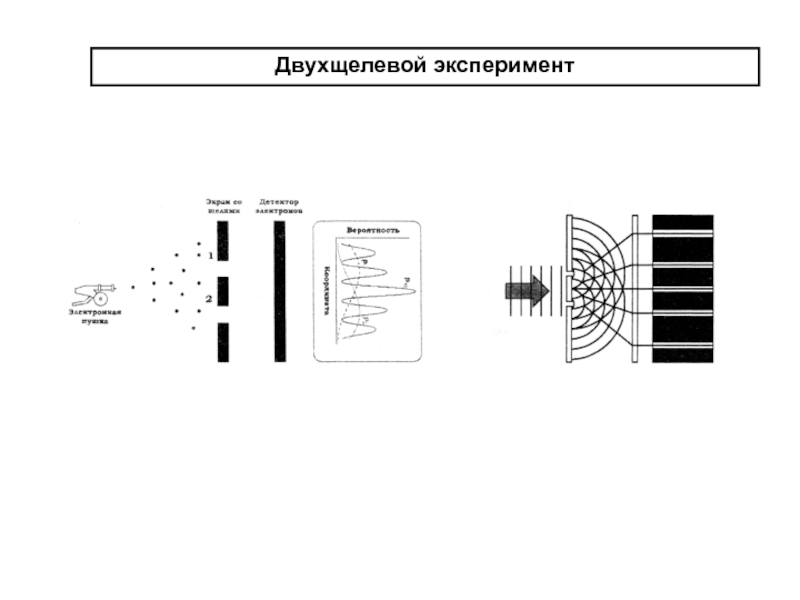
- 20. Двухщелевой эксперимент
- 21. Однако, эксперимент, проведенный в 1961
- 22. Принцип неопределенности Гейзенберга. Отличие квантовой
- 23. Ошибка в определении физической величины, налагаемая
- 24. Принцип запрета Паули. В
- 25. Однако в квантовой механике действует
- 26. Волновая функция. Необходимость вероятностного
- 27. Эти трудности можно устранить, если
- 28. Волновая функция выступает в квантовой
- 29. Описывающая состояние квантовой частицы волновая
- 30. Квантовомеханические операторы. По установившейся терминологии,
- 31. Конкретному оператору соответствует определенное множество
- 32. Если собственные значения меняются плавно
- 33. где - T - оператор
- 34. Конкретизируя в каждой из рассматриваемых
- 35. Если область, в которой могут
- 36. Отказавшись от описания движения частицы
- 37. Уравнение Шрёдингера вводится без какого-либо
- 38. Волновые функции свободных частиц.
- 39. Это уравнение оказывается чрезвычайно простым,
- 40. зависящая от времени ψ−функция приобретает
- 41. Представим k в несколько ином
- 42. Квантование энергии; частица в потенциальном
- 43. Поскольку в точке х =
- 44. Если волновой вектор k может
- 45. Слайд 45
- 46. Туннельный эффект. Теперь рассмотрим
- 47. Эта ситуация соответствует сильно обгрызанному
- 48. В квантовой механике нахождение частицы
- 49. Согласно квантовой механике волновая функция
- 50. Волновая функция при х >
- 51. Поэтому имеется конечная вероятность обнаружить
- 52. Возможность проникновения частицы в классически
- 53. При высоте барьера 2 эВ
- 54. Прохождением частиц сквозь потенциальный барьер
- 55. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Квантовая механика - это физическая теория, описывающая явления
атомного масштаба: движение элементарных частиц и состоящих из них систем.
Никто
не понимает квантовую механикуРичард Фейнман
Многие физики, учившие квантовую механику, уверены, что они её понимают, т.е. понимают то, что не понимали её отцы основатели, которые были гораздо умнее и образованнее ныне "понимающих".
Слайд 3 Наука выявляет элементы объективной рельности с помощью наблюдений,
экспериментов, измерений и на основании этого создаёт по возможности полное
описание изучаемой реальности.Квантовая механика возникла и развивалась не как описание реальности, а как описание результатов наблюдения. Она широко используется, но понимание процессов, ею описываемых, отсутствует напрочь.
Если мы что-то выучили и этим пользуемся, это совершенно не означает, что мы это понимаем. И это относится не только к студентам. И не столько к ним.
Слайд 4 Существуют две интерпретации, или концепции, квантовой механики, в
связи с вопросом о роли наблюдателя.
Эйнштейн утверждал, что
физический мир и объективная реальность существуют независимо от наблюдателя, вне его и воздействие наблюдателя картину мира не меняет, а лишь пассивно им воспринимается.В трактовке Нильса Бора (копенгагенская интерпретация) независимая от наблюдателя реальность существует в неопределённой "вероятностной" форме, приобретающей конкретное выражение только в процессе наблюдения ("редукция волновой функции").
Слайд 5 Копенгагенская интерпретация квантовой механики Нильса Бора постулирует, что
всякая надежда на достижение общей картины объективной реальности должна быть
оставлена.Квантовая теория может обеспечить только предсказание результатов измерений, но не способна обеспечить представление о том, как "природа делает это". Квантовая реальность в принципе не может быть понята в рамках прежних понятий.
Мы можем полностью игнорировать истинную действительность из-за того, что наши представления о мире не допускают ее существования.
Д. Бом
Слайд 6 Если за частицей не ведется наблюдение, она существует
в состоянии суперпозиции, то есть в нескольких состояниях и/или точках
пространства одновременно. Акт измерения "сводит" (редуцирует) волновую функцию частицы к конкретной точке или состоянию, где частица и обнаруживается, и этот переход необратим.Бом предположил, что за пределами нашей реальности существует более глубокая реальность на субквантовом уровне, ожидающая её открытия наукой. На этом уровне отсутствует локализация. Все точки пространства становятся едиными, а все частицы имеют нелокальную взаимосвязь. Такое свойство называется "нелокальностью".
Слайд 7 Классическая материальная точка это маленький, локализованный в ограниченной
области пространства субъект материи, движущийся по законам ньютоновской механики. Его
движение в пространстве является непрерывным на всех уровнях увеличения, т.е. является "континуумом".Понятие континуума легко представить, если обратиться к понятной нам всем (на первый взгляд) последовательности - числовому ряду: 1, 2, 3 …
Слайд 8 Этот ряд по большому счету и представляет собой
континуум - бесконечный непрерывный ряд чисел, не прерывающийся при любом
в него углублении до сколь угодно малых величин и различий. Рассмотрим один участок ряда, от 0 до 2. В промежутке заключено бесчисленное множество чисел, как рациональных (например 1,0 или 0,23487980076 или 0, 23487980077), так и иррациональных (например √2 и √2⁄2 и т.д.) и трансцендентных. Точно также траектория любого тела в макромеханике есть континуум, абсолютно непрерывная линия, соответствующая движению материальной точки. Точно таким же континуумом является время, оно НЕПРЕРЫВНО. Возможно и нет. Пределом делимости материи, субъектом, сохраняющим ее свойства, является атом. Идея не нова, 25 веков назад ее высказали Демокрит и Левкипп (опираясь при этом на идеи Фалеса Милетского и Анаксимена) - они изобрели первую дискретность - отдельные атомы в пустом пространстве.
Атомы состоят из элементарных частиц, которых к настоящему времени известно около 3000.
Слайд 9 В микромире наблюдаемые физиками факты не соответствуют и
не совместимы с классическим идеалом - непрерывным описанием в пространстве
и времени. В физике микромира существуют пробелы в непрерывном описании любого процесса, в пространственно-временном континууме. Поскольку микроэлектроника в качестве основного рабочего инструмента использует потоки заряженных частиц и кванты электромагнитного поля, к которым неприменимы подходы классической физики, то возникает необходимость в изучении некоторых основ квантовой механики.
Процессы в микромире, описываемые квантовой механикой, относятся к явлениям, полностью лежащим за пределами непосредственного чувственного восприятия человеческого организма и абсолютно лишены наглядности, присущей обычной классической физике.
Слайд 10 Ситуация в квантовой механике выглядит примерно следующим образом.
Наблюдаемые факты (о частицах, свете, различных видах излучения и их
взаимодействии) кажутся несовместимыми с классическим идеалом - непрерывным описанием в пространстве-времени. Процессы, субъекты и объекты квантовой механики квантованы и имеют дискретный характер, а их описание носит не детерминированный, жестко и однозначно определенный характер, а подчиняется законам статистической физики, носит вероятностный (стохастический) характер. При описании элементарных квантовых процессов теория отказалась от определяющей роли представлений о траектории движения квантовых объектов, теория описывает лишь потенциальные возможности поведения микрообъектов и, соответственно, элементарные квантовые процессы описываются лишь вероятностным, принципиально неоднозначным образом.
В квантовой физике состояния микрочастиц выражаются посредством особого рода характеристик, прежде всего - волновых функций, которые мы рассмотрим далее.
Слайд 11 С точки зрения современных знаний несовершенство классической и
квантовой механики состоит в том, что они инвариантны по отношению
ко времени.Это означает, что их уравнения обратимы во времени, что связано с тем, что они рассматривают закрытые системы, находящиеся в состоянии равновесия или стремящиеся к нему и не обменивающиеся с окружающей средой ни веществом, ни энергией, ни информацией.
В природе таких систем практически НЕТ.
Слайд 12 Мир, нас окружающий, и в котором мы живем,
представляет собой конгломерат открытых диссипативных систем, непрерывно обменивающихся энергией, веществом
и информацией и иногда исключительно далеко находящихся от равновесного состояния.Процессы в таких системах являются по большей части необратимыми, эти системы эволюционируют по определенным законам и в них присутствует так называемая стрела времени. Это означает, что они не инвариантны относительно времени.
Изучением таких эволюционирующих систем занимается нелинейная динамика.
Слайд 13 Большинство процессов в эволюционирующих системах необратимо. Самый важный вывод
заключается в том, что необратимость начинается там, где заканчиваются классическая
и квантовая механика.Это отнюдь не означает, будто классическая и квантовая механика неверны - они скорее соответствуют идеализациям, выходящим за рамки концептуальных возможностей наблюдения.
Основная идея квантовой (или волновой) механики следующая. Явление, которому классическая механика, казалось, дала адекватное описание тем, что изображала движение материальной точки, (т.е. рассматривала ее координаты х, у, z как функцию от времени) - это явление по новым представлениям должно быть изображено некоторым волновым движением, составляющимся из волн определенной частоты и скорости (и, следовательно, определенной длины волны).
Слайд 14 Обыкновенная классическая механика - только приближение, не действительное
для очень малых систем.
Цель, которая нами преследуется
заменой обычного механического описания волновым или квантово-механическим, - установить теорию, охватывающую как обыкновенные механические явления, где квантовые условия не играют заметной роли, так и типичные квантовые явления. Описание, к примеру, волнового движения световой волны посредством лучей есть лишь приближение (именуемое в случае световых волн "геометрической оптикой"), уместное только в том случае, когда структура рассматриваемого волнового явления является грубой по сравнению с длиной волны и до тех пор, пока мы интересуемся только грубой структурой.
Слайд 15 Типичные квантовые явления вполне аналогичны типичным волновым явлениям,
как дифракция и интерференция.
Для установления этой аналогии
важно то, что обычная механика неприменима как раз для очень малых систем. Критерием перехода от классической механики к квантовой (или волновой) является величина, называемая постоянной Планка, равная 6,626176⋅10-24 дж⋅сек или 10-27 эрг⋅сек и обычно обозначаемая, как h.
Слайд 16 Волновой дуализм де Бройля.
В начале
двадцатых годов двадцатого века для объяснения ряда экспериментальных данных оказалось
необходимым приписать излучению корпускулярные свойства, однако волновые свойства считались отличительной особенностью лучистой материи.В 1924 г. умер Ленин, а бельгийский принц Луи де Бройль выдвинул гипотезу об универсальности корпускулярно-волнового дуализма.
Суть гипотезы заключалась в том, что не только фотоны, но и вообще все частицы материи наряду с корпускулярными обладают также волновыми свойствами. Количественные соотношения, согласно гипотезе де Бройля, связывающие корпускулярные и волновые свойства частиц, описываются следующими выражениями:
Слайд 17 где λ - длина волны, которую можно сопоставить
с частицей; волновой вектор k направлен по движению частицы; p
- количественный импульс кванта электромагнитного излучения; ħ - квант действия, равный отношению постоянной Планка h к 2π (1,05⋅10−27 эрг⋅сек).Постоянная Планка является универсальной физической размерной константой, позволяющей количественно оценить, насколько при описании конкретной физической системы существенны квантовые эффекты.
Слайд 18 Оценим длину волны де Бройля для частицы массой
m, движущейся со скоростью V:
При прочих равных условиях
длина волны тем меньше, чем больше масса частицы. Длина волны для электрона, имеющего энергию 100 эВ составит 1,2⋅10−8 см, что является совершенно реальной величиной и может быть зафиксировано аппаратными способами. При такой же скорости движения длина волны де Бройля для пылинки с массой в 0,001 г в 1024 раз меньше.
Масса планеты Земля составляет примерно 6⋅1027 г, что на 6⋅1030 больше массы пылинки, и, соответственно, длина волны нашей планеты составит величину, на 1054 степени меньшую, чем длина волны электрона.
Величина эта не представима для нашего хилого и несовершенного разума, особенно, если учесть, что в наблюдаемой нами Вселенной число частиц составляет величину порядка 1048 (по другим данным 1080. Беда с этими теоретиками).
Слайд 19 Необходимо также заметить, что аналогично электромагнитному излучению в
любом эксперименте проявляются либо корпускулярные, либо волновые свойства любого объекта,
и никогда то и другое вместе. Эта глубокая идея была введена Нильсом Бором и получила название принципа дополнительности.Бор полагал эти взаимоисключающие идеи дополняющими друг друга, поскольку экспериментальные устройства, применяемые для наблюдения волновых свойств отличаются от устройств, применяемых для наблюдения траекторий частиц и исследования их корпускулярных свойств. Таким образом, наблюдатель выбором экспериментального оборудования как бы априори решает, какие именно свойства объекта он собирается исследовать.
Наблюдатель тем самым сильно влияет на природу, что не имеет аналога в классической физике. Вообще проблема наблюдателя в квантовой физике есть предмет многочисленных дискуссий.
Слайд 21 Однако, эксперимент, проведенный в 1961 году немецким физиком
Клаусом Йонссоном, (не сиделось гаду спокойно) явился первым из серьезных
ударов по материалистической, объективистской картине бытия, полученной в рамках классической западной науки, неотъемлемой частью которой всегда являлся постулат о существовании независимого от наблюдателя "внешнего мира".Йонссон поставил рядом с одной из щелей счетчик электронов, чтобы узнать, сколько из них пролетело через первую щель, а сколько - через вторую. В этом случае волновая интерференционная картина исчезла, и электроны вновь стали вести себя как отдельно взятые материальные объекты!
Тогда, исходя из этих результатов можно заключить, что на пути от источника к детектору электроны не существуют как "объективные" материальные объекты, находящиеся в каждый момент времени в конкретной (пусть и неизвестной нам) точке.
Ситуация принципиально иная: имеется лишь потенциальная (вероятная) возможность нахождения электрона в каждой конкретной точке, описываемая волновыми законами. Эта "потенциальность" превращается в "реальность" только в процессе наблюдения.
Слайд 22 Принцип неопределенности Гейзенберга.
Отличие квантовой частицы от обычной
заключается в том, что она не движется по определенной, строго
рассчитанной траектории, и неправомерно говорить об одновременных значениях ее координаты и импульса. В соответствии с этими представлениями Вернер Гейзенберг сформулировал принцип неопределенности, который гласит, что:Одновременное измерение начального положения и скорости квантовой частицы не может быть проведено точно. Согласно представлениям Гейзенберга в физике существуют такие пары связанных переменных, при совместном определении которых возникает конечная ошибка.
Математически принцип неопределенности Гейзенберга выражается следующим образом:
где Δх это неопределенность в координате частицы, а Δр неопределенность в ее импульсе (или точном значении энергии, что то же самое). К другой паре связанных переменных относятся изменение энергии Δε и интервала времени Δt.
Слайд 23 Ошибка в определении физической величины, налагаемая соотношением неопределенности, является
общим или взаимным свойством совокупности двух переменных.
Важная
черта принципа неопределенности заключается в том, что он является сугубо физическим принципом, он никак не связан с особенностями измерительных приборов. Его утверждение, что любое измерение содержит в себе "внутреннюю" ошибку, которая не может быть исправлена, представляет собой теорему о принципиальной ограниченности возможностей измерительных устройств.
Это - закон природы.
Слайд 24 Принцип запрета Паули.
В большинстве интересных задач,
к которым желательно было бы применить идеи микроскопической физики, фигурируют
системы с большим количеством движущихся частиц, например атомы с многими электронами, потоки электронов в микроскопически маленьком объеме твердого тела и пр.Можно было бы предположить, что если система содержит в себе не один, а много электронов, то следует рассматривать движение каждого электрона независимо от остальных, а для получения общего решения, похожего на уже когда-либо кем-либо найденное, необходимо просуммировать решения, полученные для отдельных электронов.
Тогда энергия всего атома оказалась бы просто суммой энергий электронов в их различных состояниях.
Слайд 25 Однако в квантовой механике действует совершенно иной и
существенно новый принцип (не имеющий себе аналога в классической механике)
и относящийся именно к случаю многоэлектронных атомов.Этот принцип, принцип запрета Паули, гласит, что в данный момент времени в определенном квантовом состоянии в атоме (а в общем случае в одной и той же области пространства, где действуют законы квантовой механики) может находиться лишь один электрон с полным набором квантовых чисел.
Слайд 26 Волновая функция.
Необходимость вероятностного подхода к
описанию каждой из элементарных частиц относится к любым процессам в
микромире и является одной из важнейших отличительных особенностей квантовой теории.Можно ли истолковать волны де Бройля непосредственно как волны вероятности, т.е. правильно ли считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону?
Нет, поскольку если вероятность меняется по волновому закону, то тогда вероятность обнаружения частицы для некоторых точек пространства примет отрицательные значения, что противоречит ее смыслу.
Слайд 27 Эти трудности можно устранить, если принять, что по
волновому закону меняется не сама вероятность, а некая величина, названная
амплитудой вероятности и обозначаемая обычно греческой буквой Ψ(x,y,z). Эту величину называют также волновой функцией. Амплитуда вероятности должна быть комплексной, а вероятность ω пропорциональна квадрату ее модуля:Слайд 28 Волновая функция выступает в квантовой теории как основной
носитель информации и о корпускулярных, и о волновых свойствах системы.
Вероятность dω нахождения частицы в элементе объема dV равна dω = |ψ|2⋅dV, поэтому величину |ψ|2 называют плотностью вероятности (т.е. вероятностью, отнесенной к единице объема).Предложенное Максом Борном толкование волн де Бройля исключает их понимание как классических волн материи.
Связывая со свободным электроном плоскую волну, не следует это понимать (по Борну, однако), будто бы электрон "размазан" по огромной области.
Это означает, что хотя электрон продолжает выступать в теории как точечный объект, вероятность обнаружить его в любой из точек пространства одинакова.
Это хороший кирпичик в здание гипотезы субквантового мира Дэвида Бома.
Слайд 29 Описывающая состояние квантовой частицы волновая функция ψ не
может быть непосредственно измерена, хотя выражающиеся через ψ физические величины
являются объектами экспериментальных исследований.Слайд 30 Квантовомеханические операторы.
По установившейся терминологии, некоторое математическое действие,
производимое над величиной, рассматривается как результат применения к этой величине
определенного оператора.В квантовой механике, как правило, встречаются линейные и квадратичные зависимости от импульса. Квадрат оператора понимается как знак двукратно повторенного действия этого оператора.
Как и в любой теории, дающей вероятностное описание, сопоставление с опытом производится для средних значений физических величин.
Если действие оператора на волновую функцию ψ равносильно ее умножению на некоторое число a, то ψ называют собственной функцией оператора, а число a - его собственным значением.
Слайд 31 Конкретному оператору соответствует определенное множество собственных функций и
собственных значений.
Совокупность собственных значений называют их спектром.
Таким образом, наблюдаемые на опыте значения физических величин и есть собственные значения для операторов соответствующих величин. Это положение считается настолько важным, что его часто рассматривают как отдельный постулат квантовой механики.
Слайд 32 Если собственные значения меняются плавно (непрерывно), т.е. могут
пробегать любые промежуточные значения, то их спектр называют непрерывным.
Однако наиболее интересным и специфичным именно для квантовой теории является существование дискретных спектров, которые нельзя объяснить на основе классической физики. Появление такой дискретности обусловливается чаще всего видом операторов физических величин и граничными условиями.
Слайд 33 где - T - оператор кинетической энергии, U
- оператор потенциальной энергии частицы), и уравнение для его собственных
функций ψ и собственных значений ε имеет вид: Уравнение Шрёдингера.
Важнейшим является спектр собственных значений оператора полной энергии.
Для одной частицы в заданном внешнем потенциальном поле оператор полной энергии (он называется оператором Гамильтона или гамильтонианом) является:
Это одно из основных уравнений квантовой механики и его называют уравнением Шрёдингера для стационарных состояний.
Слайд 34
Конкретизируя в каждой из рассматриваемых задач физическую природу
и особенности взаимодействия, можно установить зависимость потенциальной энергии U от
координат.Решение уравнения Шрёдингера при учете граничных условий дает весь набор собственных значений и собственных функций оператора, т.е. все возможные значения энергии физической системы.
При этом для состояний, которые отвечают так называемому финитному движению, т.е. движению частиц в ограниченной области пространства, спектр значений энергии получается дискретным.
Слайд 35 Если область, в которой могут быть обнаружены частицы,
неограниченно велика, то энергия может меняться непрерывно.
Переход
к анализу состояний позволяет не анализировать причины, происходящие в каждом конкретном акте взаимодействия, а перейти к усреднению соответствующих величин по времени и пространству. Предполагается, что именно эти усредненные значения параметров состояния и фиксируются в экспериментальных исследованиях, поэтому их использование в уравнениях позволит описывать реальные явления.
Слайд 36 Отказавшись от описания движения частицы с помощью траекторий,
получаемых из законов Ньютона, и определив вместо этого волновую функцию,
необходимо ввести в рассмотрение уравнение, эквивалентное законам Ньютона и дающее рецепт для нахождения ψ в частных физических задачах.Таковым уравнением является уравнение Шрёдингера. В одномерном случае оно имеет вид
где h - постоянная Планка, m - масса частицы, U(x) - потенциальная энергия частицы в точке х. Уравнение это записано в одномерном представлении исключительно ради простоты.
Слайд 37 Уравнение Шрёдингера вводится без какого-либо вывода и не
может быть выведено из более простых представлений точно так же,
как не могут быть выведены из каких-либо простых законов и законы Ньютона.Уравнение Шрёдингера является просто законом физики и если оно имеет смысл, то должно приводить к правильному предсказанию экспериментальных данных.
Квантовая теория не требует полного отказа от законов Ньютона, а лишь настаивает на отказе от абсолютной определенности в задании начальных условий.
Если размер и масса частицы становятся макроскопическими, предсказания квантовой и классической теории совпадают друг с другом, потому что неопределенный путь частицы становиться весьма близким к однозначной траектории.
Слайд 38 Волновые функции свободных частиц.
Можно попытаться получить
решение уравнения Шрёдингера для случаев, когда известно силовое поле, характеризующееся
потенциальной функцией U(x).Как и при использовании законов Ньютона, простейшая ситуация складывается в случае, когда сила, действующая на частицу, равна нулю.
Положим U(x) = 0 и исследуем уравнение Шрёдингера.
Оно примет следующий вид:
Слайд 39 Это уравнение оказывается чрезвычайно простым, поскольку оно имеет
тот же вид, что и уравнение, описывающее гармонический осциллятор, если
время в этом уравнении заменить на х.Решениями такого уравнения являются синус или косинус некоторого аргумента, однако по ряду соображений более удобна экспоненциальная форма.
Одним из решений (но не самым общим) является функция вида:
Слайд 40 зависящая от времени ψ−функция приобретает вид:
Эта функция описывает бегущую волну. Этот вывод является полезным сам
по себе, но, кроме того, с помощью простых соображений можно получить два в высшей степени важных соотношения. Запишем сначала эту формулу в виде:где
Здесь частота ω выражается через энергию системы. Постоянная k является также функцией энергии . Это соотношение называется соотношением Эйнштейна.
Слайд 41 Представим k в несколько ином виде; для этого
заметим, что энергия в рассматриваемом случае является кинетической энергией [U(x)=0].
Следовательно, E=p2/2m, где p - импульс частицы. Таким образом: Это соотношение называется соотношением де Бройля и устанавливает, что движение частицы носит волновой характер. Оно представляют собой концепцию корпускулярно-волнового дуализма. Сущность его можно попытаться выразить так.
Волновая функция электрона, если на него не действуют силы, представляет собой бегущую синусоидальную волну, но если электрон каким-либо образом обнаруживается в действительности, он обнаруживается как реальная и вполне локализованная частица.
Слайд 42 Квантование энергии; частица в потенциальном ящике.
Из уравнения Шрёдингера
простым способом можно вывести одно из фундаментальных положений квантовой механики,
а именно положение о квантовании энергии.Рассмотрим одномерное движение частицы; ограничим далее это движение пределами "ящика" 0 ≤ х ≤L.
Пусть потенциальная энергия бесконечна при х < 0 и x > L и равна нулю при 0 ≤ х ≤L.
Решением уравнения Шрёдингера для области 0 ≤ х ≤L является экспоненциальная функция.
Однако теперь ψ-функция должна быть равна нулю при х = 0 и при всех отрицательных значениях х, поскольку частица не может перескочить через стенки ящика.
Указанная функция должна также быть равна нулю и при всех значениях х, превышающих х = L.
Искомая функция представляет собой некоторую комбинацию синусов и косинусов:
Слайд 43 Поскольку в точке х = 0 косинус не
равен нулю, тогда как синус обращается в нуль, ψ-функция должна
быть синусоидальной функцией.Решение необходимо ограничить также рассмотрением лишь таких синусоидальных функций, которые обращаются в нуль при х > L.
Аналитически требование, налагаемое на функцию в точке х = L, выражается, так:
Волновой вектор k может принимать не все значения; разрешенными значениями являются лишь те, для которых выполняется условие:
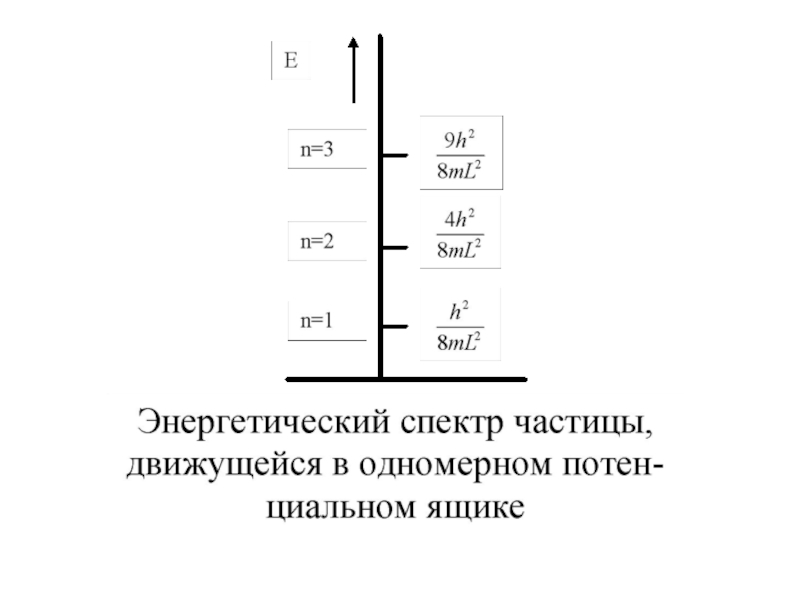
Слайд 44 Если волновой вектор k может пробегать лишь последовательность
дискретных значений, то энергия частицы также дискретна, т.е. она квантуется:
Смысл этого выражения состоит в том, что частица, движущаяся в потенциальном ящике, может обладать не произвольным значением энергии, а лишь одним из набора дискретных значений.
Энергия, таким образом, обладает дискретным спектром, который показан далее.
Причину того, что энергия совершенно свободной частицы не квантована, можно легко понять. Если длина потенциального ящика бесконечно увеличивается, то расстояние между энергетическими уровнями становится бесконечно малым.
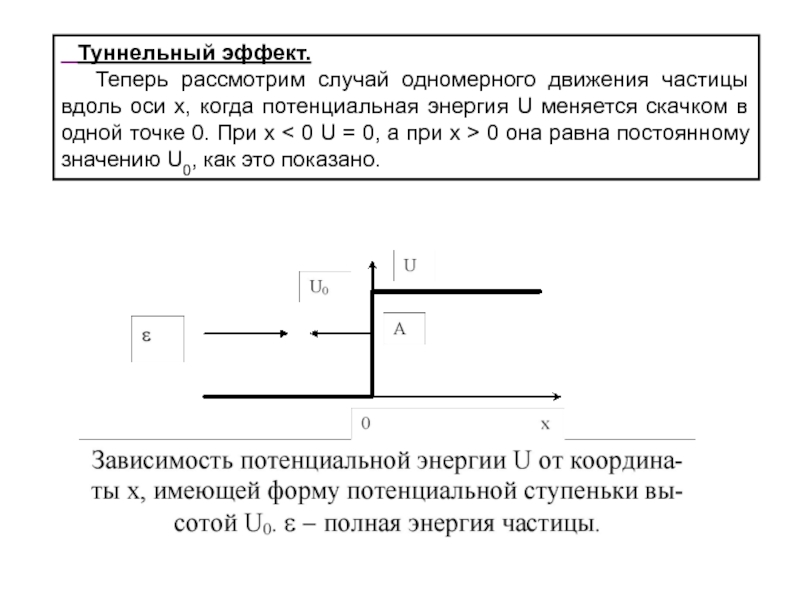
Слайд 46 Туннельный эффект.
Теперь рассмотрим случай одномерного движения
частицы вдоль оси х, когда потенциальная энергия U меняется скачком
в одной точке 0. При х < 0 U = 0, а при х > 0 она равна постоянному значению U0, как это показано.Слайд 47 Эта ситуация соответствует сильно обгрызанному одномерному потенциальному ящику,
одна стенка которого в процессе обгрызания утратилась вовсе, а вторая
имеет маленькое конкретное значение и не равна бесконечности.График зависимости потенциальной энергии от координаты х (потенциальная кривая) имеет вид ступеньки высотой U0 и называется потенциальной стенкой. Вдоль осей y и z потенциальная энергия не меняется.
Неквантовая картина движения в этом поле такова: если полная энергия частицы ε < U0, то частица, движущаяся слева направо, достигнет потенциальной стенки (в точке А) и отразится от нее. Проникнуть в область х > 0 частица не может никогда и ни при каких обстоятельствах
Слайд 48 В квантовой механике нахождение частицы внутри области ε
< U не приводит к бессмысленному выводу об отрицательной кинетической
энергии.Кинетические и потенциальные энергии, согласно соотношению неопределенностей, не имеют одновременно точных значений, так как кинетическая энергия зависит от импульса, а потенциальная энергия - от координаты.
Слайд 49 Согласно квантовой механике волновая функция частицы, движущейся к
стенке представляет собой в этой области плоскую волну де Бройля,
с импульсом равным. Зависимость волновой функции от времени при х < 0 и х > 0 одна и та же, но зависимость от координат при х > 0 становится апериодической:
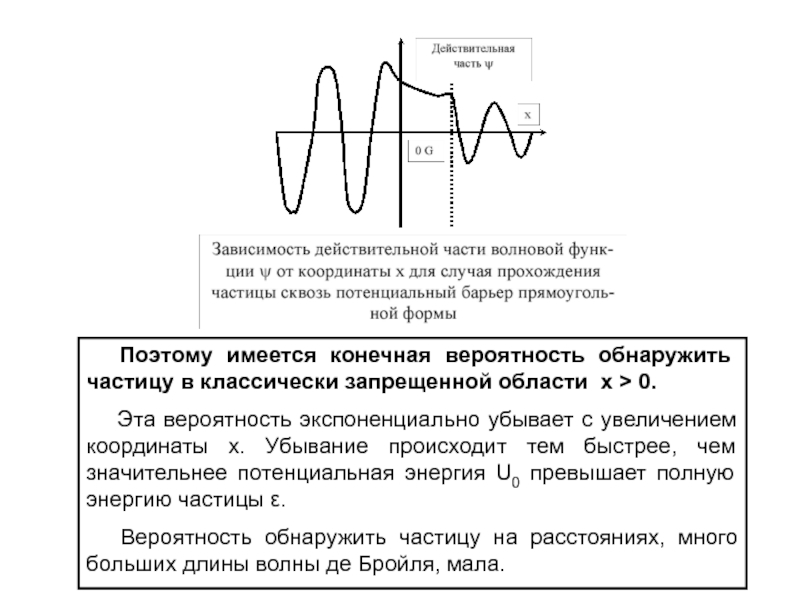
Слайд 50 Волновая функция при х > 0 экспоненциально убывает
с ростом х, как это показано на рисунке.
В пространстве перед потенциальной стенкой наряду с падающей волной существует и отраженная волна. При этом волновые функции перед стенкой (х < 0) и внутри нее (х > 0) связаны друг с другом, поскольку волновая функция не может прерываться.
В точке х = 0 значения волновых функций и значения их производных по координате должны совпадать вследствие непрерывности волновой функции и ее первой производной.
Слайд 51 Поэтому имеется конечная вероятность обнаружить частицу в классически
запрещенной области х > 0.
Эта вероятность экспоненциально убывает
с увеличением координаты х. Убывание происходит тем быстрее, чем значительнее потенциальная энергия U0 превышает полную энергию частицы ε. Вероятность обнаружить частицу на расстояниях, много больших длины волны де Бройля, мала.
Слайд 52 Возможность проникновения частицы в классически запрещенную область дает
ключ к пониманию многих процессов, существование которых, с точки зрения
классической механики, необъяснимо.В квантовой механике экспоненциально убывающая волновая функция не успевает полностью затухнуть внутри барьера и отлична от нуля в области за барьером.
Это приводит к тому, что существует небольшая вероятность обнаружить частицу за барьером.
Волновая функция при х > a также представляет собой волну де Бройля той же частоты (так как энергия частицы остается прежней), но с гораздо меньшей амплитудой, чем перед барьером, как это показано на рисунке.
Возникает любопытное для непредвзятого ума физическое явление - проникновение частиц сквозь потенциальный барьер, получившее название туннельного эффекта.
Слайд 53 При высоте барьера 2 эВ и ширине 10−8
см вероятность прохождения сквозь барьер для электрона с энергией 1
эВ равна 0,78, а для протона с той же энергией лишь 3,6⋅10−19 - величиной чудовищно маленькой.Если же взять макроскопическое тело - шарик массой в 1 г, движущийся по горизонтальной поверхности с очень маленькой скоростью (кинетическая энергия близка к нулю), то вероятность преодоления им препятствия - лезвия бритвы толщиной 0,1 мм, выступающего над горизонтальной поверхностью на 0,1 мм, равна 10−26, НО НЕ РАВНА НУЛЮ.
Слайд 54 Прохождением частиц сквозь потенциальный барьер объясняется ионизация атомов
в сильном электрическом поле, вырывание электронов из металла под действием
электрического поля (автоэлектронная эмиссия) и многие другие удивительные явления.На использовании туннельного эффекта основано действие такого мощного аналитического прибора, как сканирующий туннельный микроскоп (позволяющий проводить экспериментальные исследования на атомарном уровне) и многих других поразительных приборов, разработанных в последнее время с помощью нанотехнологии и для целей нанотехнологии и относящихся к области наноэлектроники и одноэлектроники.