Слайд 1Основные понятия
Стереометрия, или геометрия в пространстве, – это раздел геометрии,
изучающий положение, форму, размеры и свойства различных пространственных фигур.
Стереометрия -
греческое слово. Оно произошло от слов "стерео" - тело и "метрео" - измерять, т.е. буквально стереометрия означает "теломерие".
Помимо точки, прямой и плоскости, основным понятием стереометрии является пространство. Как и раньше, точки обозначаются прописными латинскими буквами A, B, C, ... . Прямые обозначаются строчными латинскими буквами a, b, c, … , или двумя большими латинскими буквами AB, CD, EF, … , указывающими точки на этих прямых. Плоскости обозначаются греческими буквами α, β, γ,
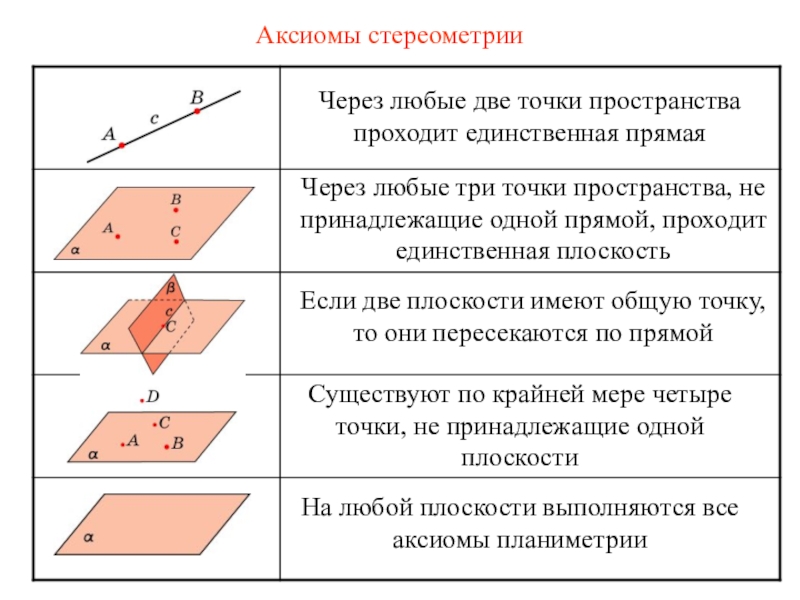
Слайд 2Аксиомы стереометрии
Через любые две точки пространства проходит единственная прямая
Через любые
три точки пространства, не принадлежащие одной прямой, проходит единственная плоскость
Если
две плоскости имеют общую точку, то они пересекаются по прямой
Существуют по крайней мере четыре точки, не принадлежащие одной плоскости
На любой плоскости выполняются все аксиомы планиметрии
Слайд 3Теорема 1
Теорема 1. Если прямая имеет с плоскостью две общие
точки, то она целиком лежит в этой плоскости.
Доказательство: Пусть
прямая a имеет с плоскостью α две общие точки А1 и А2. Так как в плоскости α выполняются аксиомы планиметрии, то в этой плоскости через точки A1, A2 проходит единственная прямая. Если бы она не совпадала с прямой а, то мы получили бы две прямые в пространстве, проходящие через две данные точки, а это противоречит аксиоме 1. Следовательно, эти прямые совпадают, и, значит, прямая а целиком лежит в плоскости α.
Слайд 4Теорема 2
Теорема 2. Через прямую и не принадлежащую ей точку
проходит единственная плоскость.
Доказательство: Пусть точка А не принадлежит прямой
a. Так как на прямой a выполняются аксиомы планиметрии, то на ней найдутся точки В, С. В силу аксиомы 2, через точки А, В, C проходит единственная плоскость α. По предыдущей теореме, прямая a лежит в плоскости α. Значит, плоскость α проходит через прямую a и точку А. Докажем, что эта плоскость единственна. Действительно, всякая плоскость, проходящая через прямую a и точку A, будет проходить также через точки В, C. По аксиоме 2 она должна совпадать с плоскостью α.
Слайд 5Упражнение 1
Сколько прямых проходит через две точки пространства?
Ответ: Одна.
Слайд 6Упражнение 2
Четыре точки не принадлежат одной плоскости. Могут ли три
из них принадлежать одной прямой?
Ответ: Нет.
Слайд 7Упражнение 3
Три вершины параллелограмма принадлежат некоторой плоскости. Верно ли, что
и четвёртая вершина этого параллелограмма принадлежит той же плоскости?
Ответ: Да.
Слайд 8Упражнение 4
Две вершины и точка пересечения диагоналей параллелограмма принадлежат одной
плоскости. Верно ли, что и две другие вершины параллелограмма принадлежат
этой плоскости?
Ответ: Нет.
Слайд 9Упражнение 5
Верно ли, что через любые две прямые проходит плоскость?
Ответ:
Нет.
Слайд 10Упражнение 6
Сколько плоскостей проходит через три точки пространства?
Ответ: Одна, если
три точки не принадлежат одной прямой; бесконечно много в противном
случае.
Слайд 11Упражнение 7
Сколько общих точек могут иметь две плоскости?
Ответ: Ни одной,
или бесконечно много.
Слайд 12Упражнение 8
Верно ли утверждение о том, что всякие: а) три
точки; б) четыре точки пространства принадлежат одной плоскости?
Ответ: а) Да;
б) нет.
Слайд 13Упражнение 9
В пространстве даны четыре точки, не принадлежащие одной плоскости.
Сколько плоскостей проходит через различные тройки из этих точек?
Ответ:
4.
Слайд 14Упражнение 10
Верно ли, что если окружность имеет с плоскостью две
общие точки, то окружность лежит в этой плоскости?
Ответ: Нет.
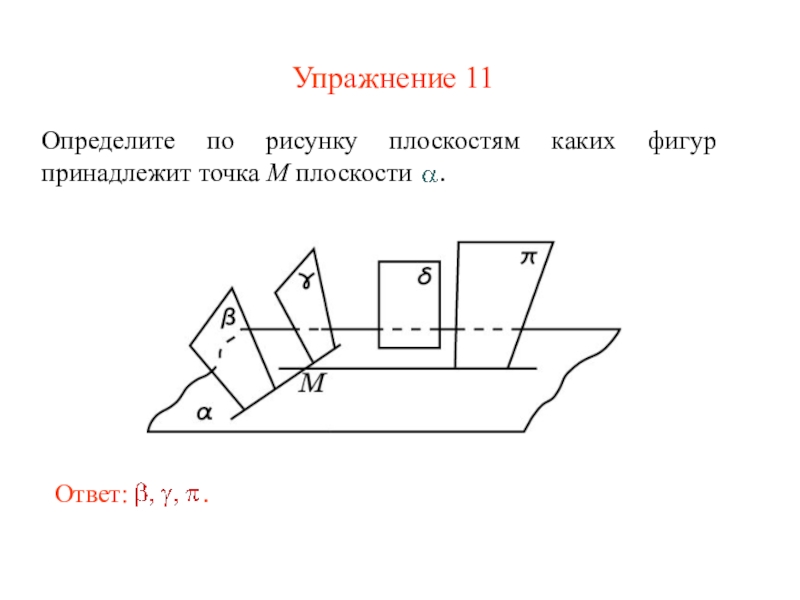
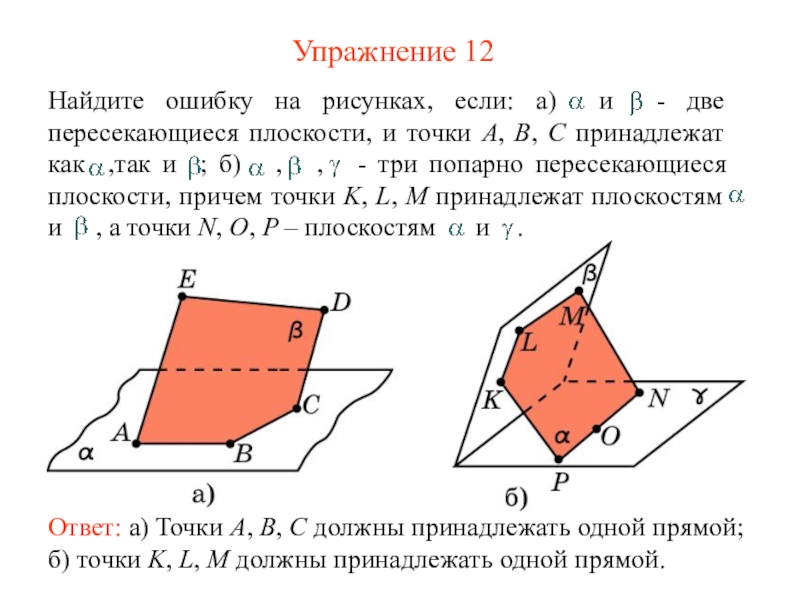
Слайд 16Упражнение 12
Ответ: а) Точки A, B, C должны принадлежать одной
прямой; б) точки K, L, M должны принадлежать одной прямой.
Слайд 17Упражнение 13
Ответ: Нет, прямая b не может пересекать прямую c.
На
рисунке попарно пересекающиеся прямые a, b, c пересекают плоскость соответственно
в точках A, B, C. Правильно ли выполнен рисунок?