Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные понятия динамики сооружений
Содержание
- 1. Основные понятия динамики сооружений
- 2. РЕКОМЕНДУЕМАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ЛИТЕРАТУРА по 3-й части курса
- 3. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ДИНАМИКИ СООРУЖЕНИЙ
- 4. Динамика сооружений -раздел строительной механики, предметом которого
- 5. Динамические воздействия - это различные по физической
- 6. Классификация динамических воздействий– по положению областей
- 7. Основные виды динамических воздействий по признаку изменения
- 8. Вынужденное движение – движение механической системы
- 9. F(t)y(t)t0t0F(t)y(t)ВынужденноедвижениеВынужденноедвижениеСвободноедвижение
- 10. Свободное движение происходит «по инерции».Инерцией (инертностью)называется свойство
- 11. Колебания (механические) – частный случай движения,характеризующийся некоторойповторяемостью во времени параметров НДС системы.F(t)y(t)y(t)t0
- 12. Периодические колебания –колебания, при которых значения некоторого
- 13. Гармонические колебания – колебания, при которых динамическиесоставляющие
- 14. Собственные колебания –частный случай свободного движения,характеризующийся синфазным
- 15. определенный вид стоячих волн,образуемых осевыми линиями
- 16. Степени свободы масс –независимые геометрические параметры,полностью определяющие
- 17. Степени свободы масс –независимые геометрические параметры,полностью определяющие
- 18. Степени свободы масс –независимые геометрические параметры,полностью определяющие
- 19. Степени свободы масс –независимые геометрические параметры,полностью определяющие
- 20. Степени свободы масс –независимые геометрические параметры,полностью определяющие
- 21. Степени свободы масс –независимые геометрические параметры,полностью определяющие
- 22. Основные задачи расчёта сооружения (конструкции)
- 23. Методы решения задач динамики– кинетостатический;– энергетический.
- 24. Кинетостатический метод – метод, основанный на использованиипринципа
- 25. Энергетический метод основан на использованииэкстремальных свойств полной механической энергии движущейся системы.
- 26. К о н т р о л
- 27. К о н т р о л
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2РЕКОМЕНДУЕМАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ЛИТЕРАТУРА по 3-й части курса строительной механики (Динамика и
устойчивость сооружений)
Учебники
1. Александров А.В., Потапов В.Д.,Зылев В.Б. Строительная механика. В
2 кн. Кн.2. Динамика и устойчивость упругих систем : учеб. для вузов / под ред. А.В. Александрова. –
М. : Высш. шк., 2008. – 384 с
2. Леонтьев Н.Н., Соболев Д.Н., Амосов А.А. Основы строительной механики
стержневых систем : учеб. для строит. спец-тей. вузов. – М. : Изд-во АСВ, 1996. – 541 с.
3. Шапошников Н.Н. Строительная механика: учебник. – 13-е изд., перераб. и доп. – СПб. :
Изд-во «Лань», 2012. – 704 с. (Предыдущие : Дарков А.В., Шапошников Н.Н. Строительная
механика. – 12-е изд., стер., 2010 . – 656 с., 12-е изд., стер., 2008. – 656 с.)
4. Киселёв В.А. Строительная механика: Спец. курс. Динамика и устойчивость сооружений. –
М. : Стройиздат, 1980. – 616 с.
Учебно-методические издания
1. Себешев В.Г. Строительная механика. Часть III. Динамика и устойчивость сооружений
( иллюстративный конспект лекций ) : учеб. пособие [Электронный ресурс]. –
Новосибирск : НГАСУ (Сибстрин), 2009. – 180 сл.
2. Себешев В.Г. Динамика деформируемых систем с конечным числом степеней свободы масс :
учеб. пособие. – Новосибирск : НГАСУ (Сибстрин), 2011. – 227 с.
3. Себешев В.Г. Расчёт стержневых систем на устойчивость методом перемещений :
учебное пособие [Электронный ресурс]. – 2-е изд., стер. – Новосибирск: НГАСУ (Сибстрин),
2013. – 84 с.
4. Крамаренко А.А., Широких Л.А. Устойчивость и динамика сооружений : сборник задач
для самостоятельной работы студентов. – Новосибирск: НГАС, 1994. – 36 с.
5. Безухов Н.И. Устойчивость и динамика в примерах и задачах :
учеб. пособие для строит. спец-тей. вузов. – М. : Высшая школа, 1987. – 264 с.
6. Роев В.И. Устойчивость упругих стержневых систем. Метод перемещений : Метод. указания
для студентов спец-ти. 2903 «Пром. и гражд. строит-во». – Новосибирск : НГАС, 1997. – 41 с.
Слайд 4Динамика сооружений -
раздел строительной механики,
предметом которого являются
принципы и
методы
исследования напряжённо-
деформированного состояния
сооружений (конструкций)
при динамических воздействиях.
Слайд 5Динамические воздействия -
это различные по физической природе
внешние вынуждающие воздействия
(силовые,
кинематические и пр.),
изменяющиеся во времени по значению,
направлению и/или месту
приложения,вызывающие движение деформируемой
механической системы и сообщающие
её массам ускорения, влиянием которых
на напряжённо-деформированное
состояние нельзя пренебрегать
(при требуемой точности расчета)
в сравнении с влиянием других
воздействий на данную систему,
неизменных во времени.
Слайд 6Классификация динамических воздействий
– по положению
областей воздействия
на сооружении
– по характеру
изменения во времени
– по длительности
воздействияподвижные
неподвижные
длительные
кратковременные
импульсивные
внезапные
по сложному закону
гармонические
– по физической природе
силовые (нагрузки)
кинематические (смещения связей)
температурные (?)
другие (электромагнитные и проч.)
Таблица
– по происхождению
природные
техногенные
Слайд 7Основные виды динамических воздействий
по признаку изменения во времени
Импульсивные
(ударные и др.)
Гармонические
(вибрационные)
F(t)
F(t)
t
t
F(t)
F(t)
t
t
TF
TF
Δt
Δt
Δt
Δt1
Δt2
Δt1
Δt2
TF
TF
Δt
Δt
Δt
Внезапно
приложенные
и внезапно
исчезающие
F(t)
F(t)
F(t)
t
t
t
TF
T0
TF
T0
Изменяющиеся
по сложному
закону
TF
TF
TF
TF
TF
F(t)
F(t)
t
t
F(t)
F(t)
t
t
TF
F(t)
t
TF
TF
TF
TF
F
F
0
0
0
0
0
0
0
0
0
0
0
0
Не существуют
Прерывистые
Непрерывные
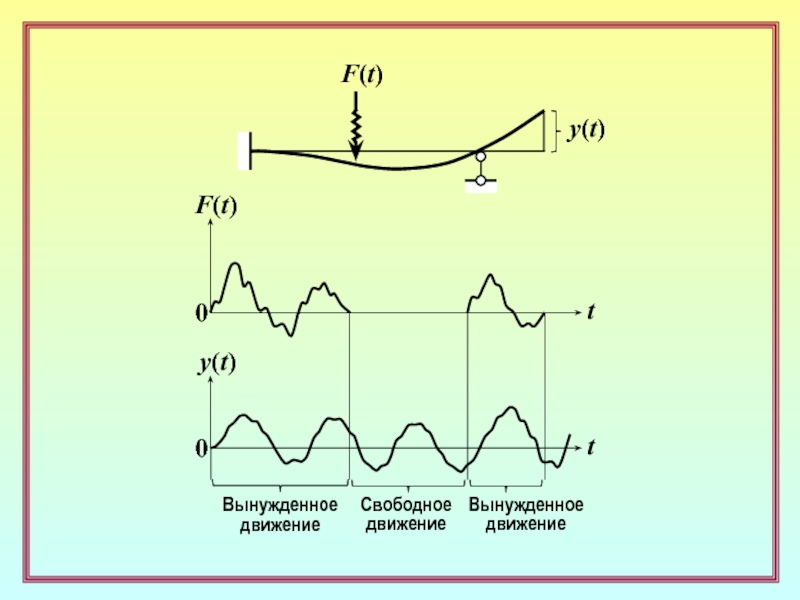
Слайд 8Вынужденное движение – движение механической системы в то время, когда
к ней
приложены динамические воздействия.
Свободное движение –
движение системы, обусловленное
начальным запасом механической энергии и происходящее без вынуждающих динамических воздействий
( в те промежутки времени, когда
динамические воздействия отсутствуют ).
Слайд 10Свободное движение происходит
«по инерции».
Инерцией (инертностью)
называется свойство материального тела
(системы), проявляющееся
в сохранении
движения, совершаемого им при отсутствии
вынуждающих воздействий, и в
постепенномизменении этого движения с течением времени
при возникновении динамических воздействий.
Мерой инерции является масса.
Следствие: свойство инерции присуще механическим,
в т.ч. деформируемым, системам, обладающим массами.
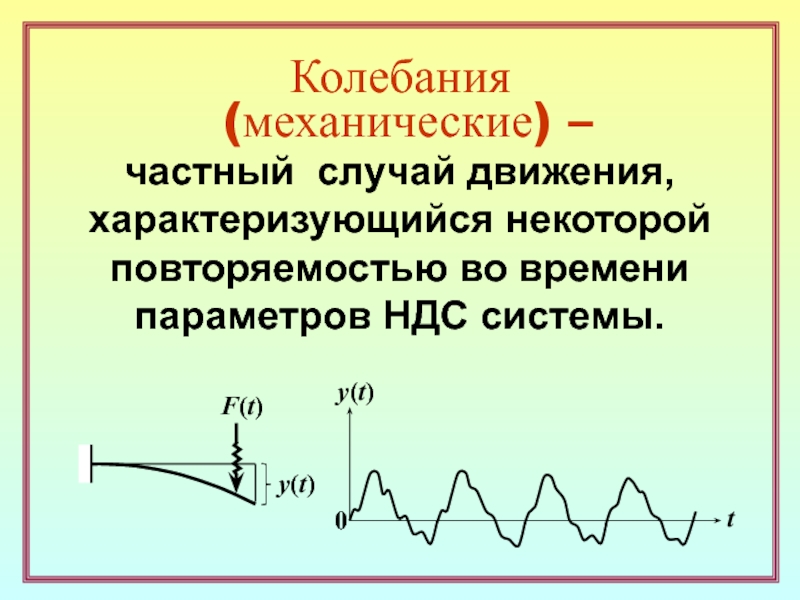
Слайд 11Колебания
(механические) –
частный случай движения,
характеризующийся некоторой
повторяемостью во времени
параметров
НДС системы.
F(t)
y(t)
y(t)
t
0
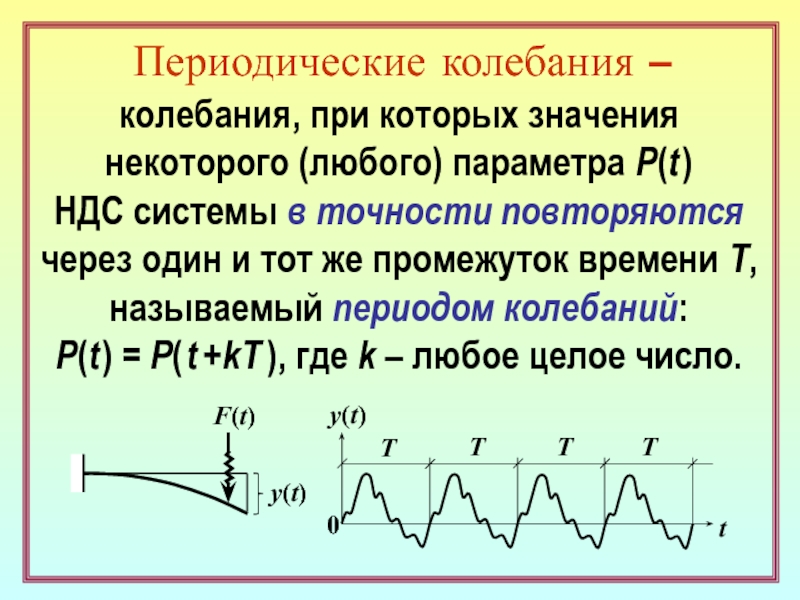
Слайд 12Периодические колебания –
колебания, при которых значения
некоторого (любого) параметра Р(t
)
НДС системы в точности повторяются
через один и тот же
промежуток времени Т, называемый периодом колебаний:
P(t ) = P( t +kT ), где k – любое целое число.
F(t)
y(t)
y(t)
t
Т
Т
Т
Т
0
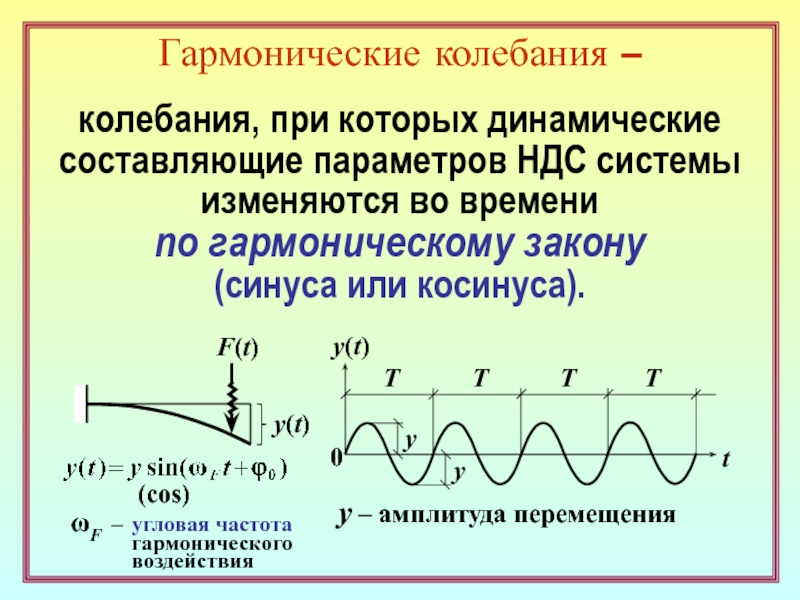
Слайд 13Гармонические колебания –
колебания, при которых динамические
составляющие параметров НДС системы
изменяются
во времени
по гармоническому закону
(синуса или косинуса).
F(t)
y(t)
y(t)
t
Т
Т
Т
Т
0
(cos)
y
y
y – амплитуда перемещения
ωF
– угловая частотагармонического
воздействия
Слайд 14Собственные колебания –
частный случай свободного движения,
характеризующийся
синфазным моногармоническим
движением всех масс
системы
(то есть гармоническим движением масс
с одной общей частотой ω и
в одной фазе ϕ (t)): yi (t) = yi sin ϕ (t), i = 1, 2, ... , n; ϕ (t) = ωt + ϕ0 . yi(t)
yk(t)
yi
yk
(стоячая волна)
i
k
ω – угловая частота собственных колебаний
Слайд 15
определенный вид стоячих волн,
образуемых осевыми линиями
или срединными поверхностями
элементов системы
при собственных колебаниях
с некоторой частотой.
Главная форма колебаний
–Слайд 16Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
Системы с распределёнными массами
Слайд 17Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
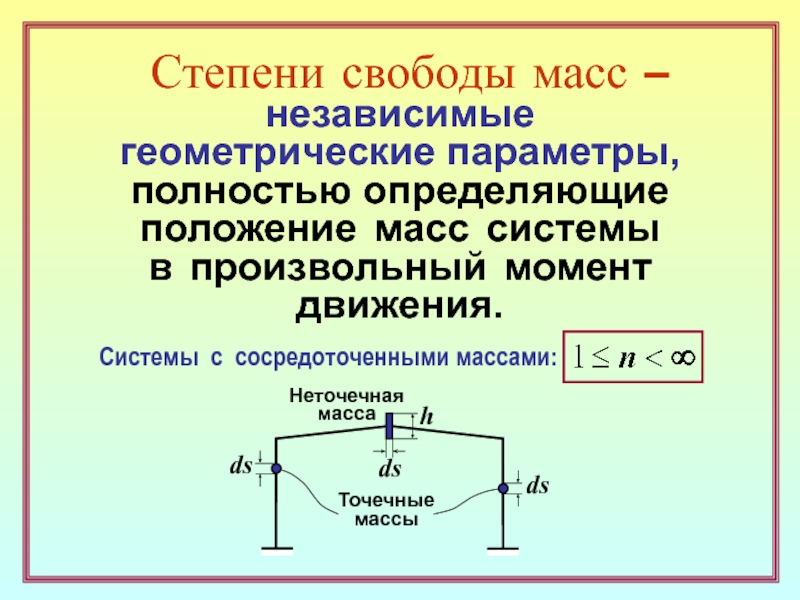
Системы с сосредоточенными массами:
Точечные
массы
Неточечная
масса
ds
ds
ds
h
Слайд 18Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
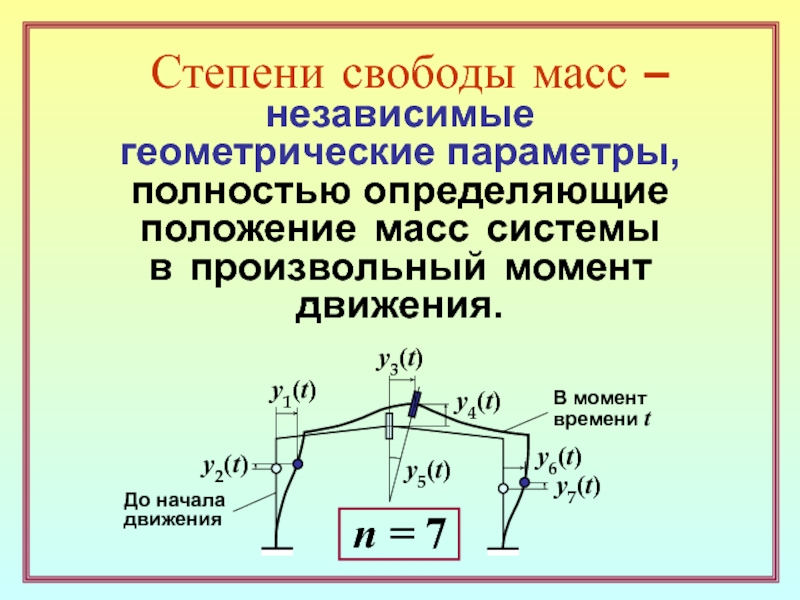
y1(t)
y3(t)
y4(t)
y5(t)
y6(t)
n = 7
y2(t)
y7(t)
До начала
движения
В момент
времени t
Слайд 19Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
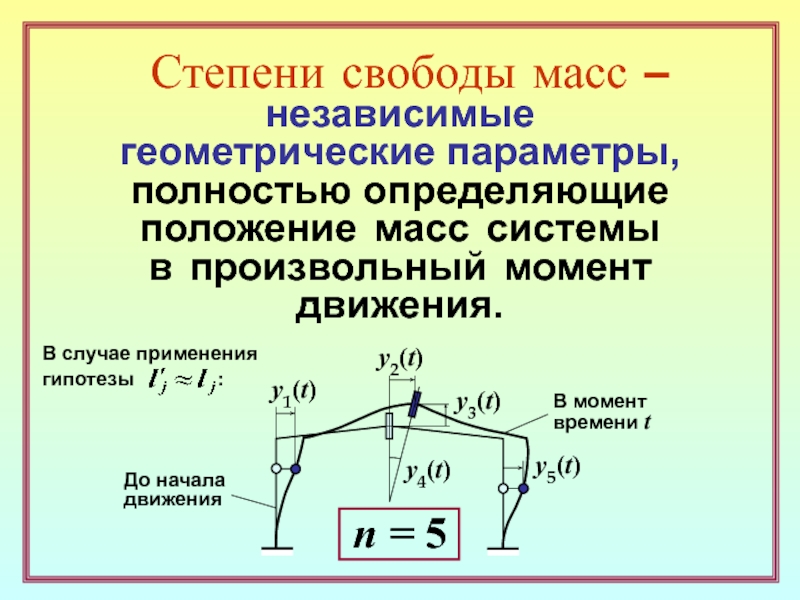
y1(t)
y2(t)
y3(t)
y4(t)
y5(t)
n = 5
В случае применения
гипотезы
:До начала
движения
В момент
времени t
Слайд 20Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
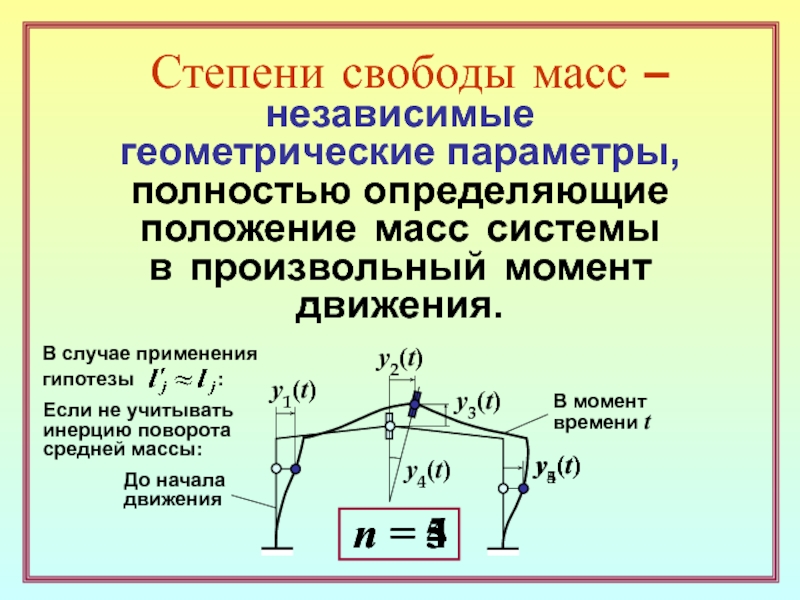
y1(t)
y2(t)
y3(t)
y4(t)
y5(t)
n = 5
В случае применения
гипотезы
:До начала
движения
В момент
времени t
Если не учитывать
инерцию поворота средней массы:
n = 4
y4(t)
Слайд 21Степени свободы масс –
независимые
геометрические параметры,
полностью определяющие
положение масс системы
в произвольный момент
движения.
n = 5
Приём определения
числа степеней свободы
масс:n можно находить как минимальное число простых связей ( линейных и угловых ), которые необходимо наложить
на массы системы для устранения
их линейной и угловой подвижности.
В случае применения
гипотезы :
Слайд 22Основные задачи
расчёта сооружения (конструкции)
на динамические воздействия
1) определение частот
и форм собственных колебаний в целях
– недопущения возникновения явления
резонанса;– определения расчётных параметров сложных динамических
воздействий (сейсмических, аэродинамических и др.);
– расчёта демпфирующих устройств (сейсмозащиты,
гасителей колебаний и т.п.);
2) выявление законов изменения перемещений, скоростей и ускорений точек сооружения, а по ним –
параметров НДС конструкций и их экстремальных значений
– для обеспечения динамической прочности (в том числе выносливости), жёсткости и устойчивости сооружения в целом и его частей;
– для предотвращения вредных ударных и вибрационных
воздействий на людей.
Слайд 24Кинетостатический метод –
метод, основанный на использовании
принципа Д’Аламбера ( J.B.L.
D’Alembert, 1743 )
и заключающийся в замене
исходной динамической задачи
условной
задачей на исследованиеравновесия системы с дополнительно
приложенными к массам инерционными
силовыми факторами (силами инерции).
Закон инерции:
П р и м е ч а н и е:
здесь и далее термин «закон инерции» используется условно, для краткости – по смысловой аналогии с физическими законами ( Гука и др. ) –
не ассоциировать с 1-м законом Ньютона.
–
ускорение
( линейное, угловое )
Слайд 25Энергетический метод
основан на использовании
экстремальных свойств
полной механической энергии движущейся
системы.
Слайд 26К о н т р о л ь н ы
е в о п р о с ы
( в
скобках даны номера слайдов, на которых можно найти ответы на вопросы;для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 26» )
1. Что является предметом науки ( учебной дисциплины ), называемой
динамикой сооружений? ( 4 )
2. Какие воздействия на сооружения и конструкции называются динамическими? ( 5 )
3. Как классифицируются динамические воздействия по различным признакам? ( 6 )
4. Основные виды динамических воздействий по характеру изменения во времени. ( 7 )
5. Что такое инерция и что является мерой инерции? ( 10 )
6. Какие механические системы обладают свойством инерции? ( 10 )
7. Какое движение механической системы называется вынужденным, а какое
свободным? ( 8 )
8. Что такое механические колебания? ( 11 )
9. Какие колебания называются периодическими? ( 12 ) гармоническими? ( 13 )
10. Дайте определение собственных колебаний. ( 14 )
11. Что такое главная форма колебаний? ( 15 )
12. Что называется степенями свободы в динамике сооружений? ( 16 )
13. Каково число степеней свободы масс (ЧССМ) системы с распределёнными
массами? ( 16 )
14. Какими должны быть массы системы, чтобы число их степеней свободы было
конечным? ( 17 )
15. Как использование различных рабочих гипотез влияет на ЧССМ? ( 17 – 20 )
16. С помощью какого практического приёма можно определять ЧССМ? ( 21 )
*) Только в режиме «Показ слайдов»
Слайд 27К о н т р о л ь н ы
е в о п р о с ы
( в
скобках даны номера слайдов, на которых можно найти ответы на вопросы;для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 27» )
16. Каковы основные задачи динамических расчётов сооружений? ( 22 )
17. Назовите общие методы решения задач динамики сооружений и объясните,
на чем базируется каждый из них. ( 23 – 25 )
18. Сформулируйте принцип Д’Аламбера. Что дает его применение в динамических
задачах расчёта сооружений? ( 24 )
19. Что такое силы инерции ( инерционные силовые факторы )
и как они определяются? ( 24 )
20. Как записывается закон инерции в общем случае движения массы? ( 24 )
*) Только в режиме «Показ слайдов»