Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Содержание
- 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
- 2. Случайные величины
- 3. Классическое определение вероятности. Вероятность случайного события равна
- 4. Статистическое определение вероятности: Вероятностью события А называется
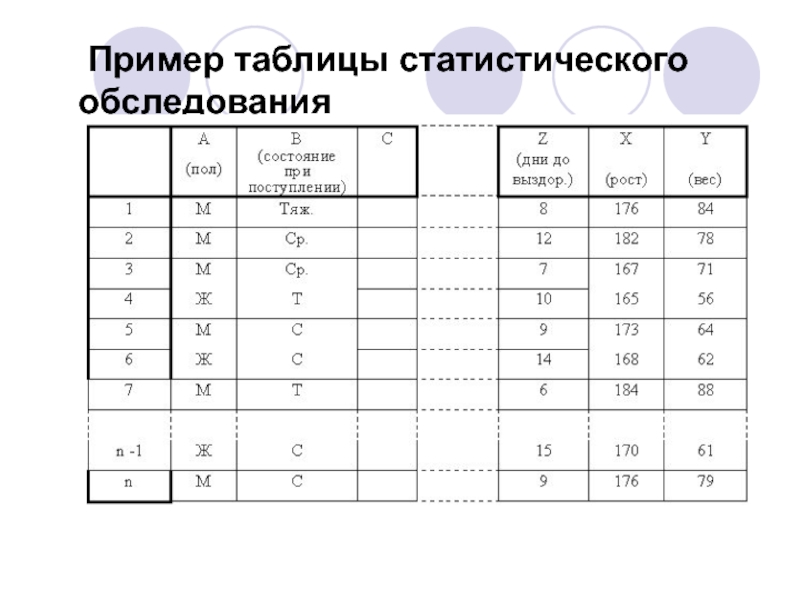
- 5. Пример таблицы статистического обследования
- 6. Понятие случайной величины Случайная величина - это количественный
- 7. Дискретные и непрерывные случайные величины Случайная величина называется
- 8. Случайная величина называется непрерывной, если она может принимать любое значение в заданном интервале.
- 9. Генеральная и выборочная совокупности Совокупность всех значений
- 10. Выборка, отражающая свойства генеральной совокупности называется представительной или репрезентативной.
- 11. Распределение случайной величины Описание совокупности значений случайной
- 12. Способы задания закона распределения случайной величиныТабличный (в
- 13. Графический (в виде графика отражающего закон распределения
- 14. Аналитический (в виде формул или специальных параметров,
- 15. Вариационные ряды В результате наблюдений или экспериментов
- 16. Статистический ряд, упорядоченный в порядке возрастания или убывания называется вариационным рядом.
- 17. Виды вариационных рядов: 1. Сгруппированный дискретный вариационный ряд2. Сгруппированный интервальный вариационный ряд
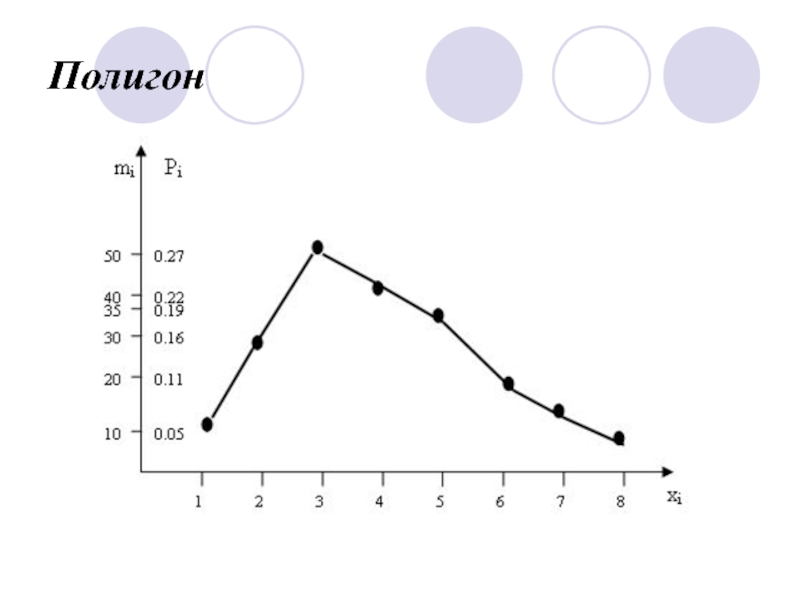
- 18. Полигон
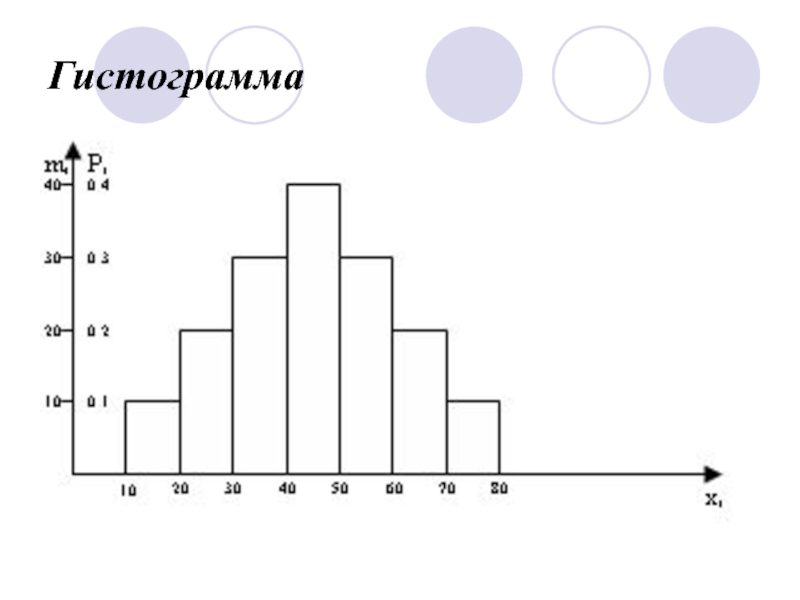
- 19. Гистограмма
- 20. Гистограмма и полигон грубо задают распределение случайной
- 21. плотность вероятности f – это параметр, показывающий,
- 22. Нормальное распределение случайной величины. Числовые характеристики нормального распределения
- 23. Если вид кривой описывается формулой ,
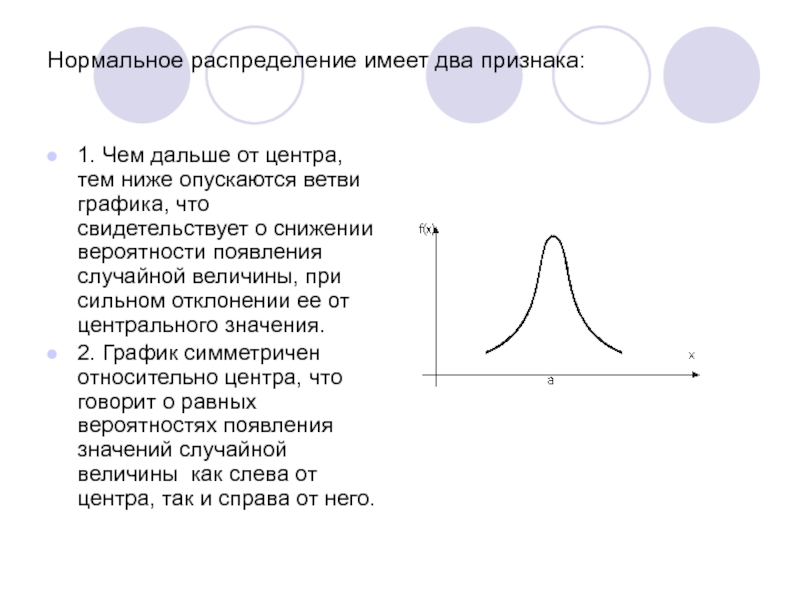
- 24. Нормальное распределение имеет два признака: 1. Чем
- 25. В формулу Гаусса входят две величины, которые
- 26. Первый параметр, обозначаемый как а, называется математическим
- 27. Если учесть, что , то получим формулу
- 28. Другой числовой характеристикой случайной величины является дисперсия, обозначаемая буквой D или σ2 (D=σ2).
- 29. где N объем генеральной совокупности. Эта величина
- 30. Корень квадратный из дисперсии называется средним
- 31. Слайд 31
- 32. Теория оценок в математической статистике
- 33. Точечные оценки параметров генеральной совокупности по выборкам
- 34. Выборочное среднее обозначают и вычисляют по формуле:где n — объем выборки.
- 35. Оценка стандартного отклонения называется выборочным стандартным отклонением
- 36. Выборочное стандартное отклонение в квадрате – это выборочная дисперсия Dx. Т.е. Dx≈D
- 37. Понятие стандартной ошибкистандартная ошибка среднего – позволяет
- 38. носит название стандартной ошибки среднего.
- 39. Интервальные оценки параметров генеральной совокупности
- 40. Интервальной оценкой СВ называется множество точечных оценок, которые накрывают неизвестный параметр.
- 41. интервал расположен симметрично относительно центра нормального распределения,
- 42. Функция ЛапласаДля решения задачи интервального оценивания перейдем
- 43. Используя параметр t, можно произвести замену переменной в функции Гаусса
- 44. график сдвигается в начало координат в точку
- 45. Тогда для нахождения вероятности попадания значения СВ
- 46. Учитывая симметричность интервала, найдем площадь от 0 до t и умножим на два
- 47. Подставим в данное выражение функцию Гаусса
- 48. Значения данного интеграла для разных t вычислил
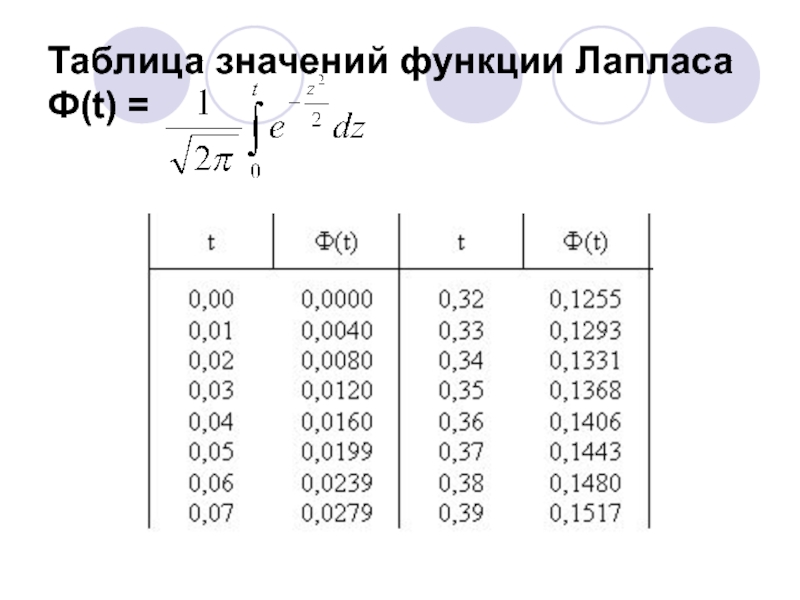
- 49. Таблица значений функции Лапласа Ф(t) =
- 50. Таким образом, вероятность нахождения неизвестного значения оцениваемого параметра генеральной совокупности можно найти по формуле: Р=2Ф(t).
- 51. Интервальные оценки математического ожидания нормального распределения при известном σ
- 52. Варианты задачи интервального оценивания при известном σ
- 53. Вариант 1Пусть необходимо найти доверительный интервал
- 54. Вариант 2Пусть необходимо найти доверительную вероятность Р
- 55. Скачать презентанцию
Случайные величины
Слайды и текст этой презентации
Слайд 3Классическое определение вероятности.
Вероятность случайного события равна отношению числа исходов
Слайд 4Статистическое определение вероятности:
Вероятностью события А называется предел отношения числа
испытаний m в которых событие А произошло к общему числу
испытаний n, при условии что общее число испытаний n стремится к бесконечности.Слайд 6Понятие случайной величины
Случайная величина - это количественный признак (параметр, переменная),
который принимает численные значения случайным образом из всех возможных значений.
Слайд 7Дискретные и непрерывные случайные величины
Случайная величина называется дискретной, если она
принимает строго определенные значения и других значений между ними быть
не может.Слайд 8
Случайная величина называется непрерывной, если она может принимать любое значение
в заданном интервале.
Слайд 9Генеральная и выборочная совокупности
Совокупность всех значений какого-то признака объектов
называется генеральной совокупностью.
Выборка – часть генеральной совокупности, взятая для исследования.
Слайд 10
Выборка, отражающая свойства генеральной совокупности называется представительной или репрезентативной.
Слайд 11Распределение случайной величины
Описание совокупности значений случайной величины с указанием
вероятности каждого значения называется законом распределения этой величины.
Слайд 12Способы задания закона распределения случайной величины
Табличный (в виде таблицы с
указанием значений случайной величины и их вероятностей или частот. На
практике такие таблицы называют вариационные ряды.)Слайд 13Графический (в виде графика отражающего закон распределения случайной величины. На
практике строят графики – Полигон и Гистограмма).
Слайд 14Аналитический (в виде формул или специальных параметров, отражающих закон распределения
случайной величины. На практике для симметричных распределений определяют величины: математическое
ожидание и дисперсия.Слайд 15Вариационные ряды
В результате наблюдений или экспериментов получают данные, которые
представляют собой множество расположенных в беспорядке чисел. Такой ряд данных
обычно называют статистическим рядом.Слайд 16 Статистический ряд, упорядоченный в порядке возрастания или убывания называется вариационным
рядом.
Слайд 17
Виды вариационных рядов:
1. Сгруппированный дискретный вариационный ряд
2. Сгруппированный интервальный
вариационный ряд
Слайд 20
Гистограмма и полигон грубо задают распределение случайной величины.
Гистограмма и
полигон могут быть построены и для дискретной и для непрерывной
случайной величины.На практике чаще для дискретной случайной величины строят полигон, а для непрерывной – гистограмму.
Слайд 21плотность вероятности f – это параметр, показывающий, какая вероятность приходится
на единицу масштаба измерения любой случайной величины, и который позволяет
всегда корректно характеризовать распределение этой случайной величины.Плотность вероятности
Слайд 22Нормальное распределение случайной величины. Числовые характеристики нормального распределения
Слайд 23Если вид кривой описывается формулой ,
то распределение
случайной величины называется нормальным. Данную функцию называют функцией Гаусса. Графиком
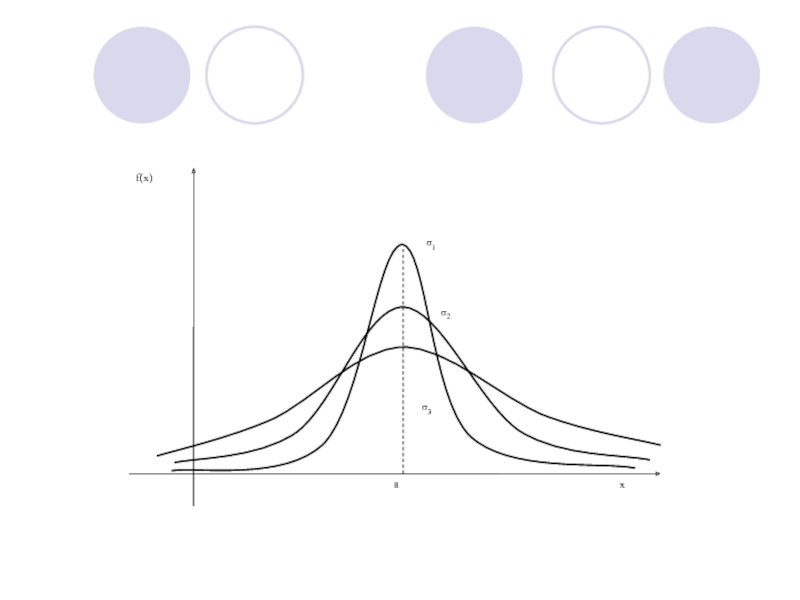
нормального распределения является колокол симметричный относительно центра распределения.Слайд 24Нормальное распределение имеет два признака:
1. Чем дальше от центра, тем
ниже опускаются ветви графика, что свидетельствует о снижении вероятности появления
случайной величины, при сильном отклонении ее от центрального значения.2. График симметричен относительно центра, что говорит о равных вероятностях появления значений случайной величины как слева от центра, так и справа от него.
Слайд 25В формулу Гаусса входят две величины, которые являются числовыми характеристиками
случайной величины или параметрами случайной величины. От их значения зависит
вид графика распределения.Слайд 26Первый параметр, обозначаемый как а, называется математическим ожиданием. Он характеризует
центр распределения случайной величины. Для нахождения математического ожидания используется формула
,где хi - значение случайной величины – роста, веса и т.д., pi – вероятность появления значения случайной величины.
Слайд 27Если учесть, что ,
то получим формулу ,
из которой
видно, что математическое ожидание – это среднее значение случайной величины
во всей ее генеральной совокупности.Слайд 28Другой числовой характеристикой случайной величины является дисперсия, обозначаемая буквой D
или σ2 (D=σ2).
Слайд 29
где N объем генеральной совокупности. Эта величина отражает меру рассеяния
значений случайной величины возле центра распределения.
Слайд 30Корень квадратный из дисперсии называется средним квадратичным отклонением (С.К.О.)
или стандартным отклонением и обозначается буквой σ (
), тогдаСлайд 33Точечные оценки параметров генеральной совокупности по выборкам
Оценка среднего
для генеральной совокупности (т.е. математического ожидания), вычисленная по выборке, называется
выборочным средним.Слайд 35Оценка стандартного отклонения называется выборочным стандартным отклонением Sx и определяется
следующим образом:
Т.е. Sx точнее соответствует σ, если в
знаменателе стоит не n, а n – 1. Приближенно можно считать Слайд 37Понятие стандартной ошибки
стандартная ошибка среднего – позволяет оценить точность, с
которой выборочное среднее характеризует значение среднего всей генеральной совокупности.
Слайд 40Интервальной оценкой СВ называется множество точечных оценок, которые накрывают неизвестный
параметр.
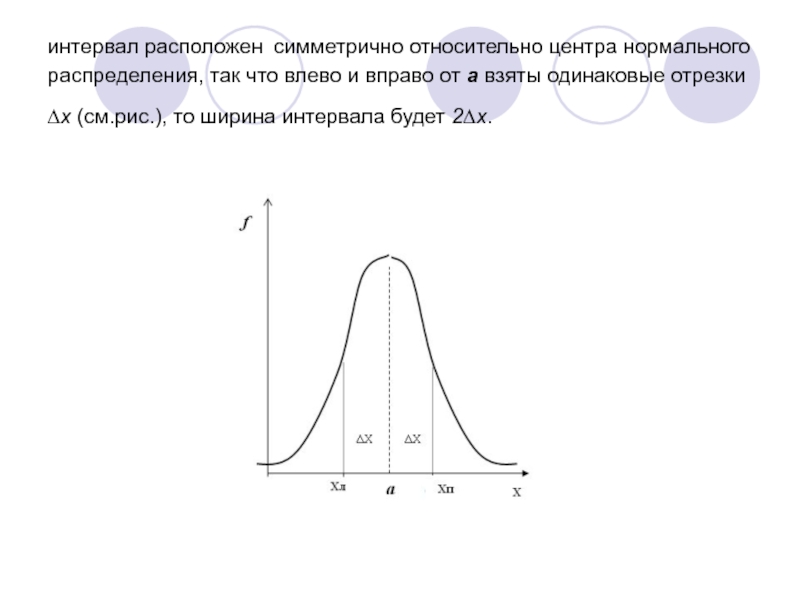
Слайд 41интервал расположен симметрично относительно центра нормального распределения, так что влево
и вправо от а взяты одинаковые отрезки ∆x (см.рис.), то
ширина интервала будет 2∆x.Слайд 42Функция Лапласа
Для решения задачи интервального оценивания перейдем от переменной x
к переменной t в функции Гаусса.
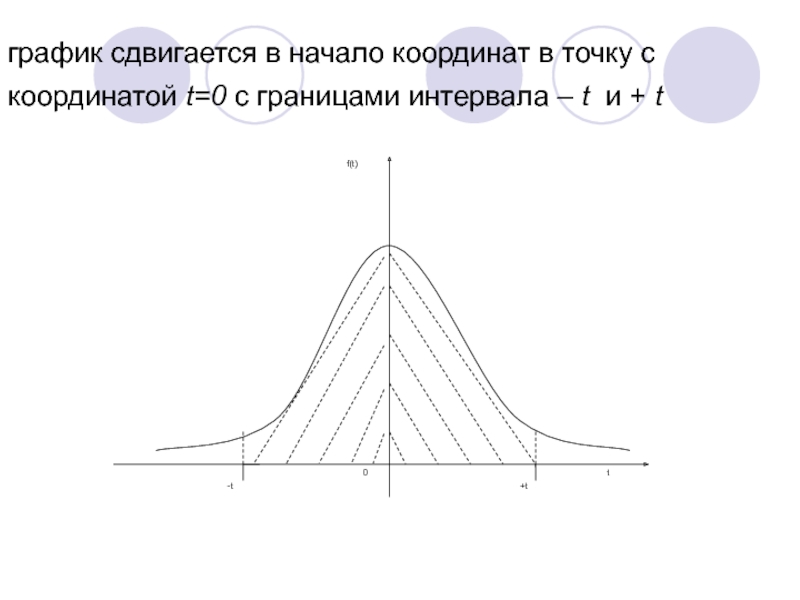
Слайд 44график сдвигается в начало координат в точку с координатой t=0
с границами интервала – t и + t
Слайд 45Тогда для нахождения вероятности попадания значения СВ в интервал от
–t до +t, проинтегрируем функцию плотности вероятности в данных пределах
Слайд 48Значения данного интеграла для разных t вычислил Лаплас и представил
их в виде таблицы. Эту таблицу можно найти в любом
математическом справочнике (см. Табл. 1). Поскольку значения этого интеграла зависят от величины верхнего предела t, то интеграл от функции Гаусса стали называть функцией Лапласа и обозначать какСлайд 50Таким образом, вероятность нахождения неизвестного значения оцениваемого параметра генеральной совокупности
можно найти по формуле: Р=2Ф(t).
Слайд 53Вариант 1
Пусть необходимо найти доверительный интервал х в котором
заключено отдельное значение некоторого параметра, для заданной доверительной вероятности Р,
если стандартное отклонение σ известно.По заданной вероятности, следует найти функцию Лапласа Ф(t)=Р/2 (вероятность нужно выражать не в процентах, а в виде десятичного числа: 0,95; 0,90 и т.д.).
По таблице Лапласа для данного значения Ф(t) выбирается t.
Определить полуширину доверительного интервала по формуле:
Определить границы доверительного интервала:
xл= a – х, xп= a + х.
Слайд 54Вариант 2
Пусть необходимо найти доверительную вероятность Р того, что отдельное
значение некоторого параметра заключено в доверительном интервале х ,
при известном значении σ.По известному значению х определить параметр t по формуле:
По таблице Лапласа для данного значения t выбирается Ф(t).
Определить доверительную вероятность по формуле: Р=2Ф(t).