Основные понятия теории вероятностей

Содержание

1. Основные понятия теории вероятностей
2. Элементарные исходыПространством элементарных исходов Ω называется множество,
3. Событиями мы будем называть некоторые наборы элементарных
4. ПримерБросаем один раз игральную кость. В этом
5. Дискретное пространствоПространство элементарных исходов назовём дискретным, если
6. События в дискретном пространстве ΩОпределение Произвольные подмножества
7. В пространстве элементарных событий Ω = {
8. Замечание Пустое множество ∅ и все множество Ω
9. Элементарные событияДостоверное событие Ω наступает при любом
10. ПримерБросаем один раз игральную кость. Выпадение более
11. ОпределенияСобытия называются равными (A1 = A2), если
12. ПримерБросаем один раз игральную кость. Событие A
13. Комбинации событийРассмотрим комбинации событий, такие, как сумма,
14. Суммой или объединением событий A1 и A2
15. ПримерБросаем один раз игральную кость. Событие A
16. Произведением или пересечением событий A1 и A2
17. ПримерВ условиях предыдущего примера:Событие A - выпадение
18. Разностью событий A1 и A2 называют событие
19. ПримерВ условиях предыдущего примера:Событие A - выпадение
20. Противоположным событием к событию A называют событие
21. ПримерВ условиях предыдущего примера:Событие A - выпадение
22. Свойства операций над событиямикоммутативностьассоциативностьдистрибутивность умножения относительно сложения
23. Слайд 23
24. Доказать свойство дистрибутивности умножения относительно сложенияРешение Докажем, что
25. Вероятность в классическом пространстве Классическая вероятность может
26. Описать пространство Ω элементарных исходов в случае
27. Решение (продолжение)Множество элементарных исходов можно задать перечислением:
28. Найти вероятность события A={суммарное число выпавших очков равно 6}.
29. По-другому этот результат можно получить, если сложить вероятности элементарных исходов
30. Замечание.Вероятность, вычисленная в этом примере, была найдена
31. Проблема!Но множество исходов не обязательно конечно или
32. Аксиоматическое определение вероятностиОпределение Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:
33. Свойства вероятности
34. Проблема!Если Ω несчетно, то не всякое подмножество
35. σ – алгебраОпределение F называется σ –алгеброй, если
36. Пример 1. {Ω, ∅}. 2. {Ω, A, Ā, ∅}, где A – некоторое подмножество Ω.
37. Аксиоматика КолмогороваОпределение Вероятностным пространством называется тройка (Ω,
38. Геометрическое вероятностное пространство Рассмотрим какую-нибудь область Ω (на
39. Эксперимент состоит в случайном выборе точки из
40. Пример Точка наудачу бросается на отрезок [0;1]. Вероятность
41. Пример Вероятность точке попасть в точку {0,5} равна
42. Пример (Задача о встрече) Два лица X и
43. Решение Будем считать интервал с 14 до
44. Можно считать, что эксперимент сводится к бросанию
45. Задача Бюффона На плоскости начерчены параллельные прямые,
46. Решение Возможные положения иглы (отрезка) на плоскости полностью
47. Обозначим через x∈[0,a] расстояние от середины иглы
48. Площадь области A⊂Ω, точки которой удовлетворяют та
49. Скачать презентанцию

Элементарные исходыПространством элементарных исходов Ω называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой ω.

Главная
Разное
Основные понятия теории вероятностей

Слайды и текст этой презентации

Слайд 1Теория вероятностей и математическая статистика
Основные понятия теории вероятностей

Слайд 2Элементарные исходы
Пространством элементарных исходов Ω называется множество, содержащее все возможные

результаты данного случайного эксперимента, из которых в эксперименте происходит ровно

один. Элементы этого множества называют элементарными исходами и обозначают буквой ω.

Элементарные исходыПространством элементарных исходов Ω называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в

Слайд 3
Событиями мы будем называть некоторые наборы элементарных исходов, то есть

подмножества множества Ω. Говорят, что в результате эксперимента произошло событие

A, если в эксперименте произошел один из элементарных исходов, входящих в множество.

Событиями мы будем называть некоторые наборы элементарных исходов, то есть подмножества множества Ω. Говорят, что в результате

Слайд 4Пример
Бросаем один раз игральную кость. В этом опыте пространство элементарных

событий Ω = {1, 2, 3, 4, 5, 6}, где

элементарное событие i - выпадение i очков.
Событие A - выпадение четного числа очков, A = {2, 4, 6},
событие B - выпадение числа очков, большего четырех, B = {5, 6}.

ПримерБросаем один раз игральную кость. В этом опыте пространство элементарных событий Ω = {1, 2, 3, 4,

Слайд 5Дискретное пространство
Пространство элементарных исходов назовём дискретным, если оно конечно или

счётно.
Множество счётно, если существует взаимно-однозначное соответствие между этим множеством

и множеством всех натуральных чисел. Счётными множествами являются, например, множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество чётных чисел и т.д. Множество конечно, если оно состоит из конечного числа элементов.

Дискретное пространствоПространство элементарных исходов назовём дискретным, если оно конечно или счётно. Множество счётно, если существует взаимно-однозначное соответствие

Слайд 6События в дискретном пространстве Ω
Определение
Произвольные подмножества дискретного

пространства элементарных исходов Ω называются событиями.

ВАЖНО:
Если Ω конечно или счётно,

то любое подмножество Ω может являться событием.

События в дискретном пространстве ΩОпределение Произвольные подмножества дискретного пространства элементарных исходов Ω называются событиями.ВАЖНО:Если Ω

Слайд 7
В пространстве элементарных событий Ω = { 1, 2, 3,

4, 5, 6 } любой набор исходов ─ событие.
Например, {1,

3, 4, 5} или { 6 }.

В пространстве элементарных событий Ω = { 1, 2, 3, 4, 5, 6 } любой набор исходов

Слайд 8
Замечание
Пустое множество ∅ и все множество Ω тоже являются событиями.

Событие ∅ называется невозможным событием, событие Ω – достоверным событием.

Замечание Пустое множество ∅ и все множество Ω тоже являются событиями. Событие ∅ называется невозможным событием, событие Ω

Слайд 9Элементарные события
Достоверное событие Ω наступает при любом исходе.
Невозможное событие

не может произойти в результате эксперимента, оно не происходит никогда.
Случайное

событие может произойти или не произойти в результате эксперимента, оно происходит иногда.

Элементарные событияДостоверное событие Ω наступает при любом исходе. Невозможное событие не может произойти в результате эксперимента, оно

Слайд 10Пример
Бросаем один раз игральную кость. Выпадение более шести очков -

невозможное событие.
Выпадение не более шести очков - достоверное событие.
Выпадение от

трех до пяти очков - случайное событие.

ПримерБросаем один раз игральную кость. Выпадение более шести очков - невозможное событие.Выпадение не более шести очков -

Слайд 11Определения
События называются равными (A1 = A2), если множества составляющих их

исходов совпадают:

События A1 и A2 называются несовместными, если их

множества элементарных исходов не пересекаются.

ОпределенияСобытия называются равными (A1 = A2), если множества составляющих их исходов совпадают: События A1 и A2 называются

Слайд 12Пример
Бросаем один раз игральную кость.
Событие A - выпадение четного

числа очков,
A = {2, 4, 6}.
Событие C - выпадение

нечетного числа очков, C = {1, 3, 5}.
A и C несовместны.

ПримерБросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = {2, 4, 6}.Событие

Слайд 13Комбинации событий
Рассмотрим комбинации событий, такие, как
сумма, произведение, разность и

т.д.
Поскольку события – это множества исходов, будем использовать соответствующие определения

для множеств.
Сумма событий соответствует объединению множеств, произведение событий соответствует пересечению множеств и т.д.

Комбинации событийРассмотрим комбинации событий, такие, как сумма, произведение, разность и т.д.Поскольку события – это множества исходов, будем

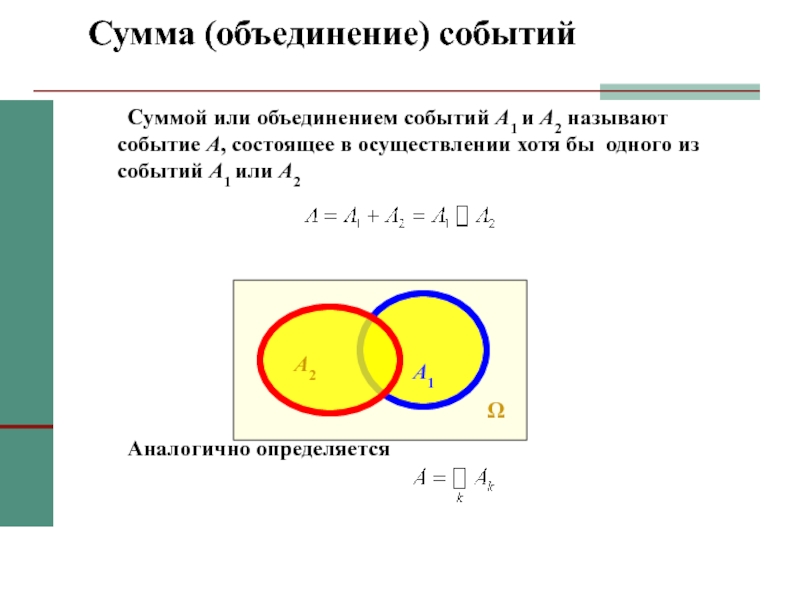
Слайд 14 Суммой или объединением событий A1 и A2 называют событие A,

состоящее в осуществлении хотя бы одного из событий A1 или

A2

Аналогично определяется

Сумма (объединение) событий

Суммой или объединением событий A1 и A2 называют событие A, состоящее в осуществлении хотя бы одного из

Слайд 15Пример
Бросаем один раз игральную кость.
Событие A - выпадение четного

числа очков, A = {2, 4, 6}.
Событие B -

выпадение числа очков, большего четырех, B = {5, 6}.
Событие A + B = {2, 4, 5, 6} состоит в том, что выпало либо четное число очков, либо число очков большее четырех, т.е. произошло либо событие A, либо событие B.

ПримерБросаем один раз игральную кость. Событие A - выпадение четного числа очков, A = {2, 4, 6}.

Слайд 16
Произведением или пересечением событий A1 и A2 называют событие A,

состоящее в осуществлении и события A1 и события A2

Аналогично

определяется

Произведение (пересечение) событий

Произведением или пересечением событий A1 и A2 называют событие A, состоящее в осуществлении и события A1 и

Слайд 17Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,

A = {2, 4, 6}.
Событие B - выпадение числа

очков, большего четырех, B = {5, 6}.
Событие A B = {6} состоит в том, что выпало четное число очков, большее четырех, т.е. произошло и событие A, и событие B.

ПримерВ условиях предыдущего примера:Событие A - выпадение четного числа очков, A = {2, 4, 6}. Событие B

Слайд 18

Разностью событий A1 и A2 называют событие A, состоящее в

том, что событие A1 осуществилось, а событие A2 – нет.

A2

A1
Ω
Разность

событий

Слайд 19Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,

A = {2, 4, 6}.
Событие B - выпадение числа

очков, большего четырех, B = {5, 6}.
Событие A\ B = {2, 4} состоит в том, что выпало четное число очков не большее четырех, т.е. произошло событие A, не произошло событие B.

Слайд 20

Противоположным событием к событию A называют событие

состоящее в том, что событие A не произошло.

A
Ω
Противоположное событие

Противоположным событием к событию A называют событие состоящее в том, что событие A не

Слайд 21Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,

A = {2, 4, 6}.
Событие =

{1, 3, 5} состоит в том, что выпало нечетное число очков, т.е. не произошло событие A.

Слайд 22Свойства операций над событиями
коммутативность
ассоциативность
дистрибутивность
умножения
относительно
сложения

Слайд 23

Слайд 24 Доказать свойство дистрибутивности умножения относительно сложения

Решение
Докажем, что событие

тождественно событию
Пусть Это означает, что

и принадлежит по крайней мере одному из событий А или В. Но тогда принадлежит хотя бы одному из событий АС или ВС, т.е. .
Наоборот, пусть , тогда принадлежит хотя бы одному из событий АС или ВС. Следовательно,
и кроме того, принадлежит по крайней мере одному из событий А или В, т.е.

Пример

Доказать свойство дистрибутивности умножения относительно сложенияРешение Докажем, что событие тождественно событию Пусть Это означает,

Слайд 25Вероятность в классическом пространстве
Классическая вероятность может быть записана как

где значок |A| обозначает число элементов в множестве A

(благоприятных исходов).

Вероятность в классическом пространстве Классическая вероятность может быть записана как где значок |A| обозначает число элементов

Слайд 26 Описать пространство Ω элементарных исходов в случае бросания двух игральных

костей.
Решение
Элементарным исходом служит упорядоченная пара чисел ω

= (i, j), где i – число очков на первой кости, j – число очков на второй кости.

Пример

Описать пространство Ω элементарных исходов в случае бросания двух игральных костей. Решение Элементарным исходом служит упорядоченная пара чисел

Слайд 27Решение (продолжение)
Множество элементарных исходов можно задать перечислением:

Слайд 28
Найти вероятность события
A={суммарное число выпавших очков равно 6}.

Слайд 29
По-другому этот результат можно получить, если сложить вероятности элементарных исходов

Слайд 30Замечание.
Вероятность, вычисленная в этом примере, была найдена с помощью классического

определения вероятности. Но классическое определение можно применять только если исходы

равновозможны. А определение (*) можно применять и при неравновозможных исходах.

Замечание.Вероятность, вычисленная в этом примере, была найдена с помощью классического определения вероятности. Но классическое определение можно применять

Слайд 31Проблема!
Но множество исходов не обязательно конечно или счетно.
Пусть, например,

опыт состоит в выборе точки из отрезка [0, 1]. Исходом

является любая точка, а множество точек отрезка несчетно. Как ввести вероятность в этом случае?

Проблема!Но множество исходов не обязательно конечно или счетно. Пусть, например, опыт состоит в выборе точки из отрезка

Слайд 32Аксиоматическое определение вероятности
Определение
Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:

Слайд 33Свойства вероятности

Слайд 34Проблема!
Если Ω несчетно, то не всякое подмножество Ω является событием.
А

какие же подмножества являются событиями?
Ответ: только такие, которые входят в

так называемые σ–алгебры.

Проблема!Если Ω несчетно, то не всякое подмножество Ω является событием.А какие же подмножества являются событиями?Ответ: только такие,

Слайд 35σ – алгебра
Определение
F называется σ –алгеброй, если

Слайд 36Пример
1. {Ω, ∅}.
2. {Ω, A, Ā, ∅}, где A –

некоторое подмножество Ω.

Слайд 37Аксиоматика Колмогорова
Определение
Вероятностным пространством называется тройка (Ω, F, P),
где

Ω – пространство элементарных событий,
F – σ–алгебра подмножеств множества Ω,
P

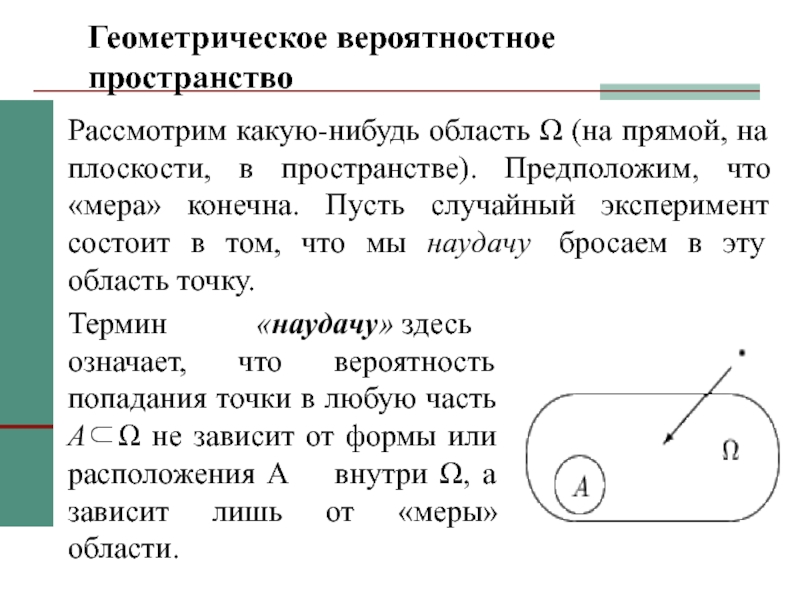
– вероятностная мера, заданная на F.

Аксиоматика КолмогороваОпределение Вероятностным пространством называется тройка (Ω, F, P), где Ω – пространство элементарных событий, F – σ–алгебра

Слайд 38Геометрическое вероятностное пространство

Рассмотрим какую-нибудь область Ω (на прямой, на плоскости,

в пространстве). Предположим, что «мера» конечна. Пусть случайный эксперимент состоит

в том, что мы наудачу бросаем в эту область точку.

Термин «наудачу» здесь означает, что вероятность попадания точки в любую часть A⊂Ω не зависит от формы или расположения A внутри Ω, а зависит лишь от «меры» области.

Геометрическое вероятностное пространство Рассмотрим какую-нибудь область Ω (на прямой, на плоскости, в пространстве). Предположим, что «мера» конечна. Пусть

Слайд 39 Эксперимент состоит в случайном выборе точки из ограниченного множества Ω;
F

– система подмножеств Ω, у которых существует мера (длина, площадь,

объем и т.д. );

где ||A|| – мера множества A.

Эксперимент состоит в случайном выборе точки из ограниченного множества Ω; F – система подмножеств Ω, у которых существует

Слайд 40Пример
Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в

отрезок
[0,1; 0,5] равна 4/10 = 0,4. (Почему?)
А чему

равна вероятность точке попасть в полуоткрытый интервал [0,1; 0,5)?
Тоже 4/10 = 0,4.

Пример Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в отрезок [0,1; 0,5] равна 4/10 =

Слайд 41Пример
Вероятность точке попасть в точку {0,5} равна нулю, так как

мера множества, состоящего из одной точки («длина точки»), есть 0.

Вместе с тем попадание в точку {0,5} не является невозможным событием — это один из элементарных исходов эксперимента.

Пример Вероятность точке попасть в точку {0,5} равна нулю, так как мера множества, состоящего из одной точки («длина

Слайд 42Пример (Задача о встрече)
Два лица X и Y условились встретиться

в определенном месте между двумя и тремя часами дня. Пришедший

первым ждет другого в течении 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?

Пример (Задача о встрече) Два лица X и Y условились встретиться в определенном месте между двумя и тремя

Слайд 43Решение
Будем считать интервал с 14 до 15 часов дня

отрезком [0,1] длиной 1 час. Пусть ξ и η –

моменты прихода X и Y (точки отрезка [0,1]).

Все возможные результаты эксперимента – множество точек квадрата со стороной 1:

Ω={(ξ,η): 0≤ ξ ≤1, 0≤ η ≤1} = [0,1]x[0,1]

Решение Будем считать интервал с 14 до 15 часов дня отрезком [0,1] длиной 1 час. Пусть ξ

Слайд 44
Можно считать, что эксперимент сводится к бросанию точки наудачу в

квадрат. При этом благоприятными исходами являются точки множества
A={(ξ,η): |ξ

– η| ≤1/6}
То есть попадание в множество A наудачу брошенной в квадрат точки означает, что X и Y встретятся. Тогда вероятность встречи равна

Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки

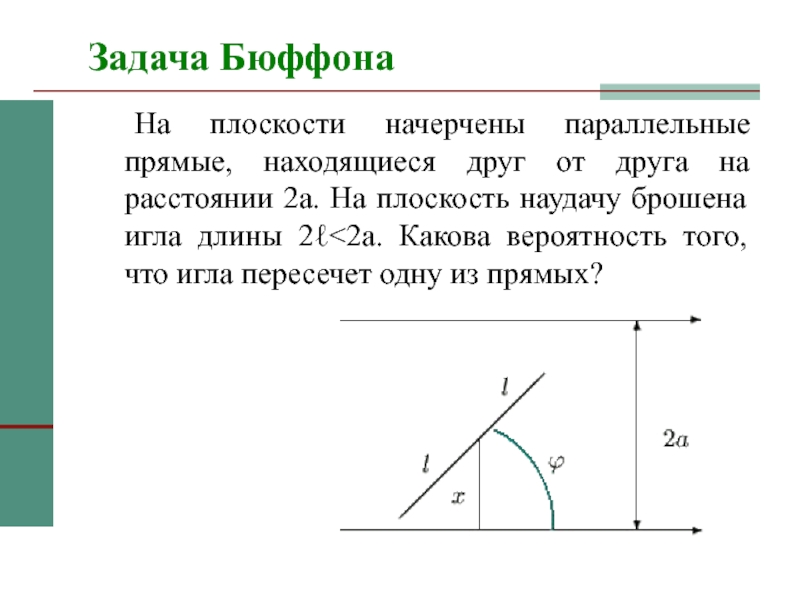
Слайд 45Задача Бюффона
На плоскости начерчены параллельные прямые, находящиеся друг от

друга на расстоянии 2a. На плоскость наудачу брошена игла длины

2ℓ<2a. Какова вероятность того, что игла пересечет одну из прямых?

Задача Бюффона На плоскости начерчены параллельные прямые, находящиеся друг от друга на расстоянии 2a. На плоскость наудачу

Слайд 46Решение
Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины

иглы и углом поворота иглы относительно какого –либо направления. Причем

две эти переменные (положение центра и угол поворота) меняются независимо друг от друга.

Решение Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины иглы и углом поворота иглы относительно какого

Слайд 47
Обозначим через x∈[0,a] расстояние от середины иглы до ближайшей прямой,

а через ϕ∈[0,π] – угол между каким –то направлением прямых

и иглой. Множество возможных положений иглы целиком определяется выбором наудачу точки из прямоугольника
Ω = [0,a]x[0,π].

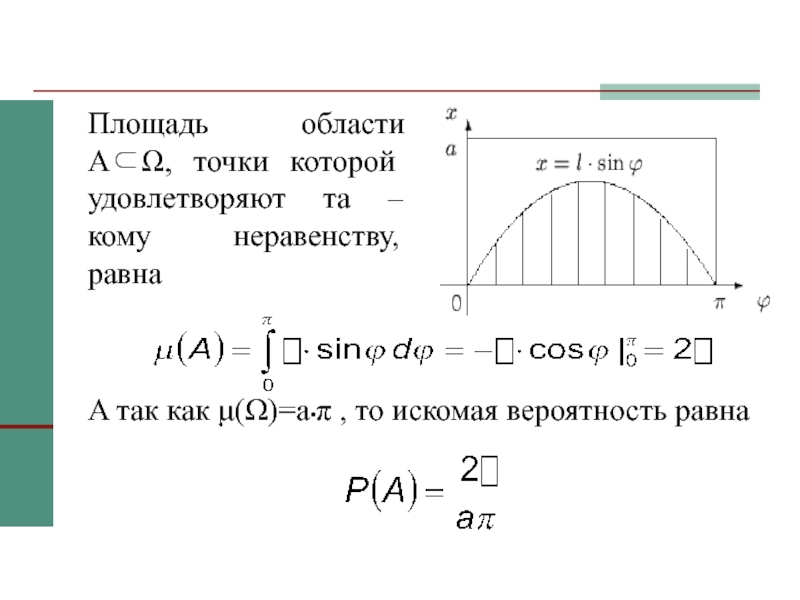
Игла пересекает ближайшую прямую, если координаты выбранной наудачу точки удовлетворяют неравенству: x ≤ ℓ•sin ϕ.

Обозначим через x∈[0,a] расстояние от середины иглы до ближайшей прямой, а через ϕ∈[0,π] – угол между каким

Слайд 48
Площадь области A⊂Ω, точки которой удовлетворяют та –кому неравенству, равна

A так как μ(Ω)=a•π , то искомая вероятность равна

Площадь области A⊂Ω, точки которой удовлетворяют та –кому неравенству, равна A так как μ(Ω)=a•π , то искомая

Скачать презентацию

Разделы презентаций

Основные понятия теории вероятностей

Содержание

Слайды и текст этой презентации

Слайд 1Теория вероятностей и математическая статистикаОсновные понятия теории вероятностей

Слайд 2Элементарные исходыПространством элементарных исходов Ω называется множество, содержащее все возможные

результаты данного случайного эксперимента, из которых в эксперименте происходит ровно

Слайд 3Событиями мы будем называть некоторые наборы элементарных исходов, то есть

подмножества множества Ω. Говорят, что в результате эксперимента произошло событие

Слайд 4ПримерБросаем один раз игральную кость. В этом опыте пространство элементарных

событий Ω = {1, 2, 3, 4, 5, 6}, где

Слайд 5Дискретное пространствоПространство элементарных исходов назовём дискретным, если оно конечно или

счётно. Множество счётно, если существует взаимно-однозначное соответствие между этим множеством

Слайд 6События в дискретном пространстве ΩОпределение Произвольные подмножества дискретного

пространства элементарных исходов Ω называются событиями.ВАЖНО:Если Ω конечно или счётно,

Слайд 7В пространстве элементарных событий Ω = { 1, 2, 3,

4, 5, 6 } любой набор исходов ─ событие.Например, {1,

Слайд 8Замечание Пустое множество ∅ и все множество Ω тоже являются событиями.

Событие ∅ называется невозможным событием, событие Ω – достоверным событием.

Слайд 9Элементарные событияДостоверное событие Ω наступает при любом исходе. Невозможное событие

не может произойти в результате эксперимента, оно не происходит никогда.Случайное

Слайд 10ПримерБросаем один раз игральную кость. Выпадение более шести очков -

невозможное событие.Выпадение не более шести очков - достоверное событие.Выпадение от

Слайд 11ОпределенияСобытия называются равными (A1 = A2), если множества составляющих их

исходов совпадают: События A1 и A2 называются несовместными, если их

Слайд 12ПримерБросаем один раз игральную кость. Событие A - выпадение четного

числа очков, A = {2, 4, 6}.Событие C - выпадение

Слайд 13Комбинации событийРассмотрим комбинации событий, такие, как сумма, произведение, разность и

т.д.Поскольку события – это множества исходов, будем использовать соответствующие определения

Слайд 14 Суммой или объединением событий A1 и A2 называют событие A,

состоящее в осуществлении хотя бы одного из событий A1 или

Слайд 15ПримерБросаем один раз игральную кость. Событие A - выпадение четного

числа очков, A = {2, 4, 6}. Событие B -

Слайд 16 Произведением или пересечением событий A1 и A2 называют событие A,

состоящее в осуществлении и события A1 и события A2 Аналогично

Слайд 17ПримерВ условиях предыдущего примера:Событие A - выпадение четного числа очков,

A = {2, 4, 6}. Событие B - выпадение числа

Слайд 18 Разностью событий A1 и A2 называют событие A, состоящее в

том, что событие A1 осуществилось, а событие A2 – нет. A2A1ΩРазность

Слайд 19ПримерВ условиях предыдущего примера:Событие A - выпадение четного числа очков,

A = {2, 4, 6}. Событие B - выпадение числа

Слайд 20 Противоположным событием к событию A называют событие

состоящее в том, что событие A не произошло.AΩПротивоположное событие

Слайд 21ПримерВ условиях предыдущего примера:Событие A - выпадение четного числа очков,

A = {2, 4, 6}. Событие =

Слайд 22Свойства операций над событиямикоммутативностьассоциативностьдистрибутивность умножения относительно сложения

Слайд 23

Слайд 24 Доказать свойство дистрибутивности умножения относительно сложенияРешение Докажем, что событие

тождественно событию Пусть Это означает, что

Слайд 25Вероятность в классическом пространстве Классическая вероятность может быть записана как

где значок |A| обозначает число элементов в множестве A

Слайд 26 Описать пространство Ω элементарных исходов в случае бросания двух игральных

костей. Решение Элементарным исходом служит упорядоченная пара чисел ω

Слайд 27Решение (продолжение)Множество элементарных исходов можно задать перечислением:

Слайд 28 Найти вероятность события A={суммарное число выпавших очков равно 6}.

Слайд 29По-другому этот результат можно получить, если сложить вероятности элементарных исходов

Слайд 30Замечание.Вероятность, вычисленная в этом примере, была найдена с помощью классического

определения вероятности. Но классическое определение можно применять только если исходы

Слайд 31Проблема!Но множество исходов не обязательно конечно или счетно. Пусть, например,

опыт состоит в выборе точки из отрезка [0, 1]. Исходом

Слайд 32Аксиоматическое определение вероятностиОпределение Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:

Слайд 33Свойства вероятности

Слайд 34Проблема!Если Ω несчетно, то не всякое подмножество Ω является событием.А

какие же подмножества являются событиями?Ответ: только такие, которые входят в

Слайд 35σ – алгебраОпределение F называется σ –алгеброй, если

Слайд 36Пример 1. {Ω, ∅}. 2. {Ω, A, Ā, ∅}, где A –

некоторое подмножество Ω.

Слайд 37Аксиоматика КолмогороваОпределение Вероятностным пространством называется тройка (Ω, F, P), где

Ω – пространство элементарных событий, F – σ–алгебра подмножеств множества Ω, P

Слайд 38Геометрическое вероятностное пространство Рассмотрим какую-нибудь область Ω (на прямой, на плоскости,

в пространстве). Предположим, что «мера» конечна. Пусть случайный эксперимент состоит

Слайд 39 Эксперимент состоит в случайном выборе точки из ограниченного множества Ω; F

– система подмножеств Ω, у которых существует мера (длина, площадь,

Слайд 40Пример Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в

отрезок [0,1; 0,5] равна 4/10 = 0,4. (Почему?)А чему

Слайд 41Пример Вероятность точке попасть в точку {0,5} равна нулю, так как

мера множества, состоящего из одной точки («длина точки»), есть 0.

Слайд 42Пример (Задача о встрече) Два лица X и Y условились встретиться

в определенном месте между двумя и тремя часами дня. Пришедший

Слайд 43Решение Будем считать интервал с 14 до 15 часов дня

Слайд 1Теория вероятностей и математическая статистика
Основные понятия теории вероятностей

Слайд 2Элементарные исходы
Пространством элементарных исходов Ω называется множество, содержащее все возможные

Слайд 3
Событиями мы будем называть некоторые наборы элементарных исходов, то есть

Слайд 4Пример
Бросаем один раз игральную кость. В этом опыте пространство элементарных

Слайд 5Дискретное пространство
Пространство элементарных исходов назовём дискретным, если оно конечно или

счётно.
Множество счётно, если существует взаимно-однозначное соответствие между этим множеством

Слайд 6События в дискретном пространстве Ω
Определение
Произвольные подмножества дискретного

пространства элементарных исходов Ω называются событиями.

ВАЖНО:
Если Ω конечно или счётно,

Слайд 7
В пространстве элементарных событий Ω = { 1, 2, 3,

4, 5, 6 } любой набор исходов ─ событие.
Например, {1,

Слайд 8
Замечание
Пустое множество ∅ и все множество Ω тоже являются событиями.

Слайд 9Элементарные события
Достоверное событие Ω наступает при любом исходе.
Невозможное событие

не может произойти в результате эксперимента, оно не происходит никогда.
Случайное

Слайд 10Пример
Бросаем один раз игральную кость. Выпадение более шести очков -

невозможное событие.
Выпадение не более шести очков - достоверное событие.
Выпадение от

Слайд 11Определения
События называются равными (A1 = A2), если множества составляющих их

исходов совпадают:

События A1 и A2 называются несовместными, если их

Слайд 12Пример
Бросаем один раз игральную кость.
Событие A - выпадение четного

числа очков,
A = {2, 4, 6}.
Событие C - выпадение

Слайд 13Комбинации событий
Рассмотрим комбинации событий, такие, как
сумма, произведение, разность и

т.д.
Поскольку события – это множества исходов, будем использовать соответствующие определения

Слайд 15Пример
Бросаем один раз игральную кость.
Событие A - выпадение четного

числа очков, A = {2, 4, 6}.
Событие B -

Слайд 16
Произведением или пересечением событий A1 и A2 называют событие A,

состоящее в осуществлении и события A1 и события A2

Аналогично

Слайд 17Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,

A = {2, 4, 6}.
Событие B - выпадение числа

Слайд 18

Разностью событий A1 и A2 называют событие A, состоящее в

том, что событие A1 осуществилось, а событие A2 – нет.

A2

A1
Ω
Разность

Слайд 19Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,

A = {2, 4, 6}.
Событие B - выпадение числа

Слайд 20

Противоположным событием к событию A называют событие

состоящее в том, что событие A не произошло.

A
Ω
Противоположное событие

Слайд 21Пример
В условиях предыдущего примера:
Событие A - выпадение четного числа очков,

A = {2, 4, 6}.
Событие =

Слайд 22Свойства операций над событиями
коммутативность
ассоциативность
дистрибутивность
умножения
относительно
сложения

Слайд 24 Доказать свойство дистрибутивности умножения относительно сложения

Решение
Докажем, что событие

тождественно событию
Пусть Это означает, что

Слайд 25Вероятность в классическом пространстве
Классическая вероятность может быть записана как

костей.
Решение
Элементарным исходом служит упорядоченная пара чисел ω

Слайд 27Решение (продолжение)
Множество элементарных исходов можно задать перечислением:

Слайд 28
Найти вероятность события
A={суммарное число выпавших очков равно 6}.

Слайд 29
По-другому этот результат можно получить, если сложить вероятности элементарных исходов

Слайд 30Замечание.
Вероятность, вычисленная в этом примере, была найдена с помощью классического

Слайд 31Проблема!
Но множество исходов не обязательно конечно или счетно.
Пусть, например,

Слайд 32Аксиоматическое определение вероятности
Определение
Вероятность события есть числовая функция P(A), удовлетворяющая аксиомам:

Слайд 34Проблема!
Если Ω несчетно, то не всякое подмножество Ω является событием.
А

какие же подмножества являются событиями?
Ответ: только такие, которые входят в

Слайд 35σ – алгебра
Определение
F называется σ –алгеброй, если

Слайд 36Пример
1. {Ω, ∅}.
2. {Ω, A, Ā, ∅}, где A –

Слайд 37Аксиоматика Колмогорова
Определение
Вероятностным пространством называется тройка (Ω, F, P),
где

Ω – пространство элементарных событий,
F – σ–алгебра подмножеств множества Ω,
P

Слайд 38Геометрическое вероятностное пространство

Рассмотрим какую-нибудь область Ω (на прямой, на плоскости,

Слайд 39 Эксперимент состоит в случайном выборе точки из ограниченного множества Ω;
F

Слайд 40Пример
Точка наудачу бросается на отрезок [0;1]. Вероятность точке попасть в

отрезок
[0,1; 0,5] равна 4/10 = 0,4. (Почему?)
А чему

Слайд 41Пример
Вероятность точке попасть в точку {0,5} равна нулю, так как

Слайд 42Пример (Задача о встрече)
Два лица X и Y условились встретиться

Слайд 43Решение
Будем считать интервал с 14 до 15 часов дня

Слайд 44
Можно считать, что эксперимент сводится к бросанию точки наудачу в

квадрат. При этом благоприятными исходами являются точки множества
A={(ξ,η): |ξ

Слайд 45Задача Бюффона
На плоскости начерчены параллельные прямые, находящиеся друг от

Слайд 46Решение
Возможные положения иглы (отрезка) на плоскости полностью определяются положением середины

Слайд 47
Обозначим через x∈[0,a] расстояние от середины иглы до ближайшей прямой,

Слайд 48
Площадь области A⊂Ω, точки которой удовлетворяют та –кому неравенству, равна