Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основоположник теории потока однородных событий
Содержание
- 1. Основоположник теории потока однородных событий
- 2. Свойство марковости
- 3. Непрерывный Марковский процессРассмотрим два состояния Марковской цепи
- 4. Непрерывный Марковский процессРассмотрим систему из n состояний
- 5. Непрерывный Марковский процесс
- 6. Непрерывный Марковский процесс
- 7. Непрерывный Марковский процесс в сбалансированном режиме
- 8. Пример расчета стационарных вероятностей для непрерывного Марковского
- 9. Пример расчета стационарных вероятностей для непрерывноного Марковского
- 10. Пример расчета стационарных вероятностей для непрерывного Марковского
- 11. Системы массового обслуживания (СМО)
- 12. Основоположник теории массового обслуживания Андре́й Никола́евич Колмого́ров (1903—1987)Профессор
- 13. Основоположник теории массового обслиживанияАнгер Краруп Эрланг (1878—1929)Датский математик
- 14. Процесс гибели и размножения – снова СМОПроцесс
- 15. Процесс гибели и размножения – основа СМОРешение
- 16. Системы массового обслуживания (СМО)Системы массового обслуживания (СМО)
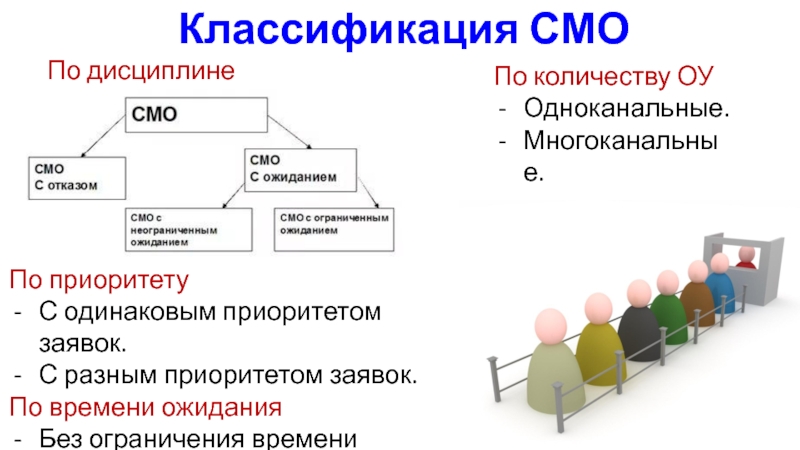
- 17. Классификация СМОПо дисциплине обслуживанияПо количеству ОУОдноканальные.Многоканальные.По приоритетуС
- 18. Классификация СМОВ ТМО существуют стандартные обозначения классов
- 19. Пример СМО
- 20. Пример СМО
- 21. Формула Литтла
- 22. Одноканальная СМО с отказами (M/M/1)
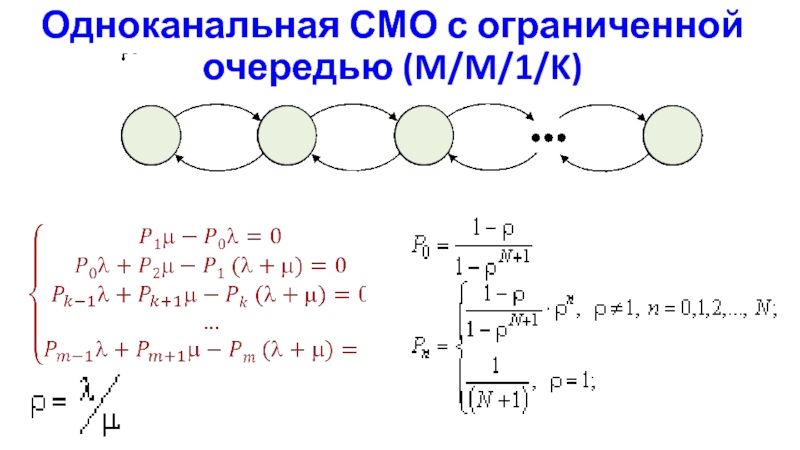
- 23. Одноканальная СМО с ограниченной очередью (M/M/1/K)
- 24. Одноканальная СМО с ограниченной очередьюPотк=РN= относительная
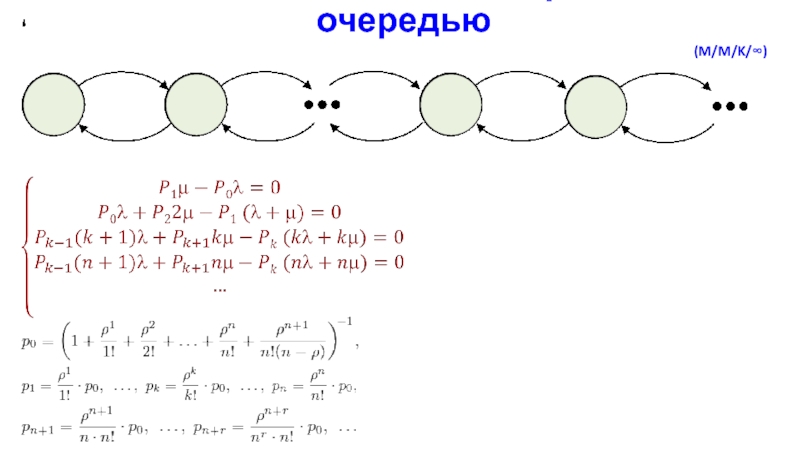
- 25. Одноканальная СМО с неограниченной очередью (M/M/1/)
- 26. Одноканальная СМО с неограниченной очередьюСреднее число заявок
- 27. Пример расчета одноканальной СМО с неограниченной очередьюВ
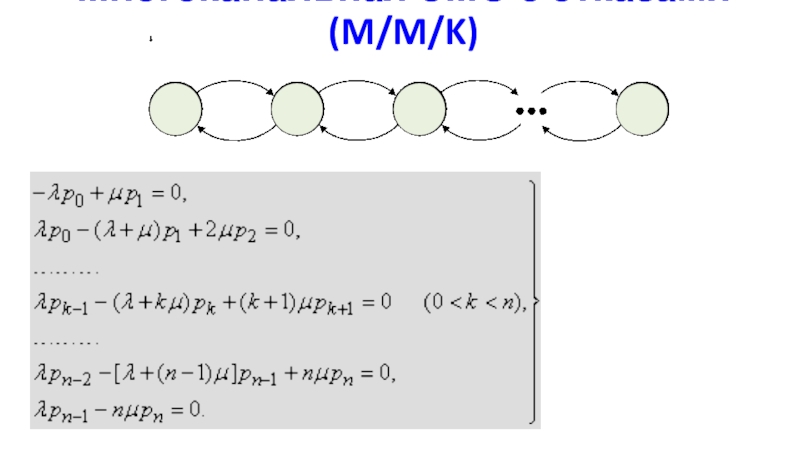
- 28. Многоканальная СМО с отказами (M/M/K)
- 29. Многоканальная СМО с отказами (M/M/K)Формула Эрланга!
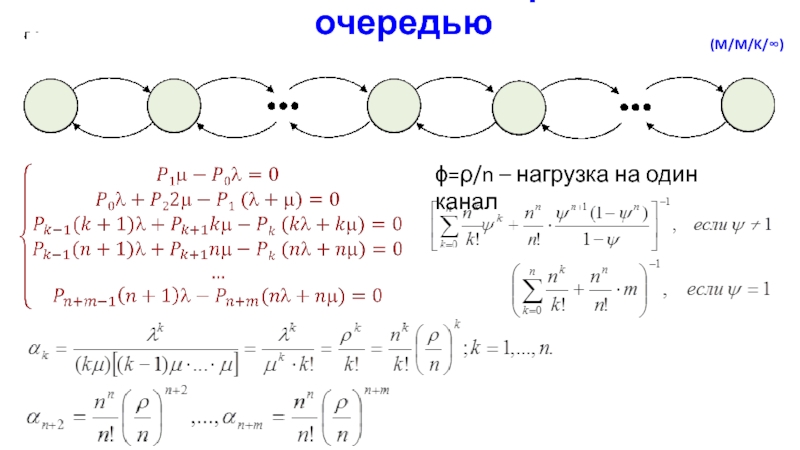
- 30. Многоканальная СМО с ограниченной очередью=/n – нагрузка на один канал(M/M/K/)
- 31. Многоканальная СМО с ограниченной очередью (M/M/K/L)Среднее число занятых работой ОУ
- 32. Многоканальная СМО с неограниченной очередью(M/M/K/)
- 33. Многоканальная СМО с неограниченной очередьюСреднее число занятых каналов(M/M/K/)
- 34. Литература1. Вентцель Е.С., Овчаров Л.А. Теория случайных
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Основоположник теории потока однородных событий
Александр Яковлевич Хи́нчин (1894—1959)
профессор МГУ с
1927 года.
создатель теории случайных процессов и теории массового обслуживания.Слайд 3Непрерывный Марковский процесс
Рассмотрим два состояния Марковской цепи si и si.
Переход из состояния в состояние происходит под воздействием пуассоновского потока
с интенсивностью ij. Пуассоновский поток обладает свойством отсутствием последействия, поэтому нам не надо будет заботиться о том, как система попала в состояние si.Рассмотрим элементарный участок на оси времени t, примыкающий в точке времени t. Вероятность того, что система, находящаяся в состоянии si, перейдет в состояние si будет равна ijPi.
Слайд 4Непрерывный Марковский процесс
Рассмотрим систему из n состояний s1…sn. Пусть имеется
имеются интенсивности переходов между каждыми двумя состояниями ij (ij), если
две вершина не связаны, то интенсивность переходов между ними равна нулю. Обозначим pi(t) вероятность того, система в момент t находится в состоянии si (i=1…n). Пусть pi(t+t) вероятность того, что система будет в состоянии si в момент t+t. Обозначим эту вероятность A:A={S(t+t)=si}.Событие A состоит из суммы двух возможных событий (A=B+C):
B – система уже была в состоянии si и за время t не вышла из него.
C – система была в одном из состоянии, из которых возможен переход в состояние si и за время t она перешла в состояние si.
Выясним вероятность события B
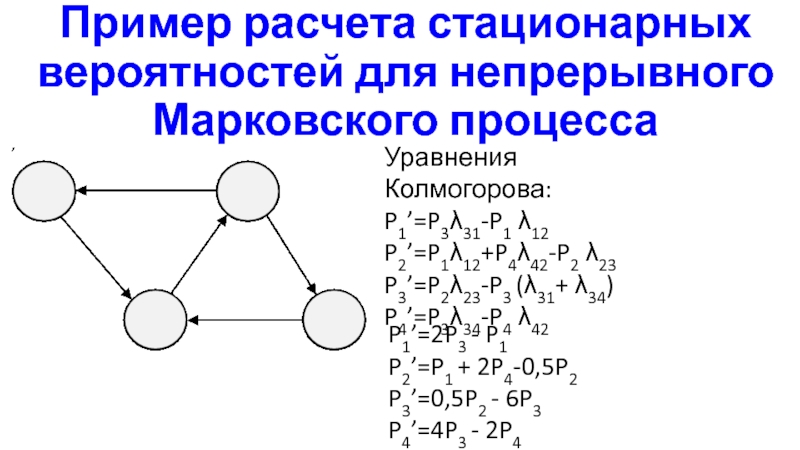
Слайд 8Пример расчета стационарных вероятностей для непрерывного Марковского процесса
Уравнения Колмогорова:
P1’=P331-P1 12
P2’=P112+P442-P2
23
P3’=P223-P3 (31+ 34)
P4’=P334-P4 42
P1’=2P3 - P1
P2’=P1 + 2P4-0,5P2
P3’=0,5P2 - 6P3
P4’=4P3
- 2P4Слайд 9Пример расчета стационарных вероятностей для непрерывноного Марковского процесса
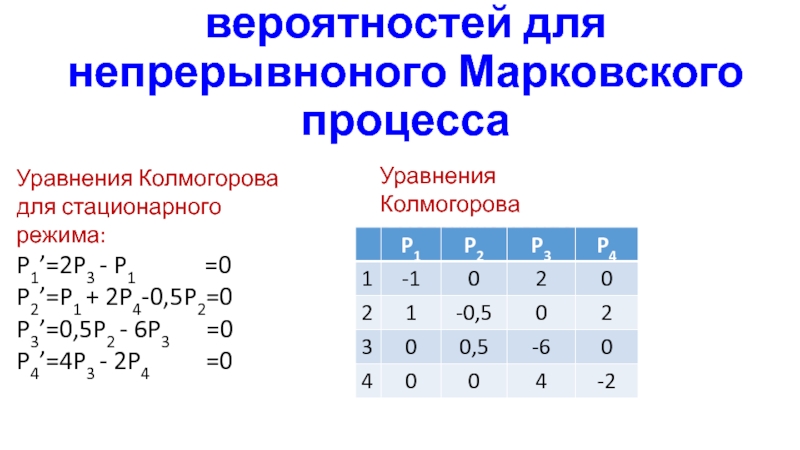
Уравнения Колмогорова
для стационарного
режима:
P1’=2P3 - P1
=0P2’=P1 + 2P4-0,5P2=0
P3’=0,5P2 - 6P3 =0
P4’=4P3 - 2P4 =0
Уравнения Колмогорова
в матричном виде
Слайд 10Пример расчета стационарных вероятностей для непрерывного Марковского процесса
Заменим одну строку
матрицы на условие нормировки, добавим столбец свободных членов, все элементы
которого равны 0 кроме ячейки напротив строки с условием нормировки. Решим систему уравнений и получаем стационарные вероятности.Слайд 12Основоположник теории массового обслуживания
Андре́й Никола́евич Колмого́ров (1903—1987)
Профессор МГУ с 1931
года.
Один из крупнейших математиков XX века.
Один из основоположников современной теории
вероятностей.Создатель теории случайных процессов и теории массового обслуживания.
Слайд 13Основоположник теории массового обслиживания
Ангер Краруп Эрланг (1878—1929)
Датский математик и инженер, один
из основателей ТМО.
1909 год – опубликована работа «Теория вероятностей и
телефонные разговоры» (The Theory of Probabilities and Telephone Conversations.) , получившая признание во всем мире.В его честь названа единица измерения трафика в телекоммуникационных системах – эрланг. 1 эрланг (1 Эрл) эквивалентен разговору двух абонентов в течение 1 часа.
Формулой Эрланга пользуются до сих пор.
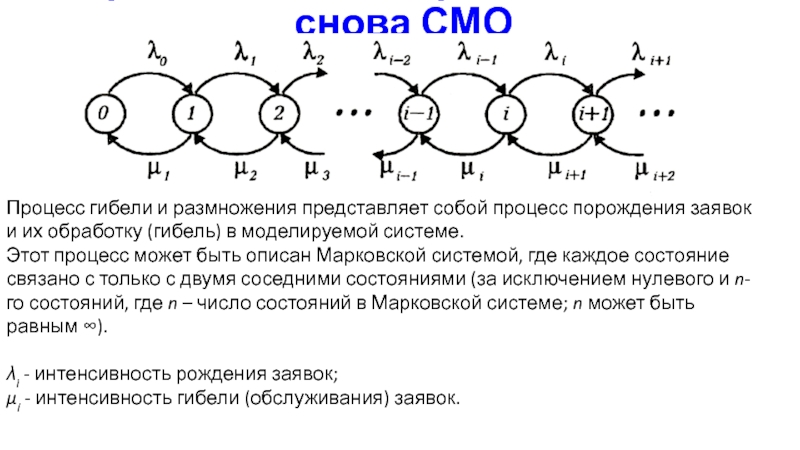
Слайд 14Процесс гибели и размножения – снова СМО
Процесс гибели и размножения
представляет собой процесс порождения заявок и их обработку (гибель) в
моделируемой системе.Этот процесс может быть описан Марковской системой, где каждое состояние связано с только с двумя соседними состояниями (за исключением нулевого и n-го состояний, где n – число состояний в Марковской системе; n может быть равным ).
i - интенсивность рождения заявок;
i - интенсивность гибели (обслуживания) заявок.
Слайд 15Процесс гибели и размножения – основа СМО
Решение системы уравнений:
Система уравнений
Колмогорова для стационарного состояния системы рождения и гибели
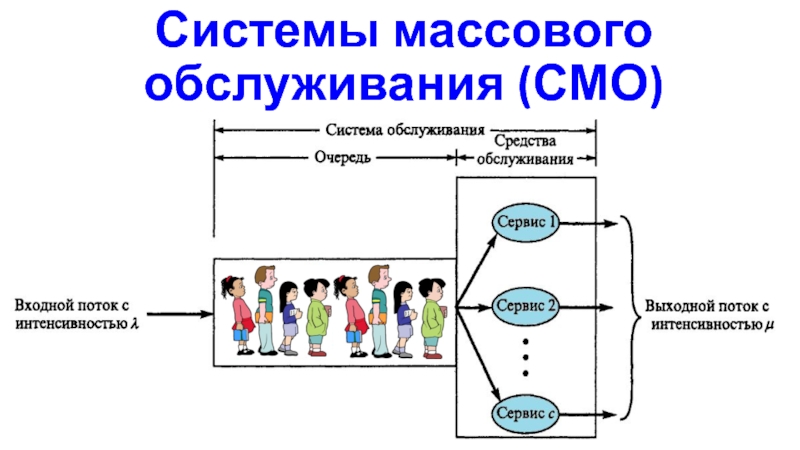
Слайд 16Системы массового обслуживания (СМО)
Системы массового обслуживания (СМО) или теория массового
обслуживания (ТМО) – это частный случай непрерывной Марковской системы. ТМО
рассматривает наиболее часто встречающийся на практике случай – процессы гибели и размножения.СМО – это системы из трёх типов элементов:
Источник заявок (ИЗ) - порождает поток заявок.
Обслуживающее устройство (ОУ) – обслуживает заявки.
Очередь ожидания (Оч.). В очередь попадают заявки, в случае занятости ОУ облуживанием предыдущей заявки.
Слайд 17Классификация СМО
По дисциплине обслуживания
По количеству ОУ
Одноканальные.
Многоканальные.
По приоритету
С одинаковым приоритетом заявок.
С
разным приоритетом заявок.
По времени ожидания
Без ограничения времени ожидания.
С ограничением времени
ожидания.Слайд 18Классификация СМО
В ТМО существуют стандартные обозначения классов СМО:
A/B/m
Или
A/B/m/K/M, где
A,B –
тип потока входящих событий и дисциплины обслуживания.
m – количество ОУ
в СМО.K – количество мест для заявок в очереди
Типы потока заявок:
M – простейший поток.
Er – поток Эрланга порядка r.
D – детерминированное.
HR- гиперпоказательное порядка R.
G – распределение произвольного типа.
Слайд 24Одноканальная СМО с ограниченной очередью
Pотк=РN=
относительная пропускная способность
абсолютная пропускная
способность: А=q∙λ
среднее число находящихся в системе заявок:
среднее время пребывания заявки
в системе:средняя продолжительность пребывания клиента (заявки) в очереди: Wq=Ws- 1/μ;
среднее число заявок (клиентов) в очереди (длина очереди): Lq=λ(1-PN)Wq.
(M/M/1/K)
Слайд 26Одноканальная СМО с неограниченной очередью
Среднее число заявок в системе
Среднее время
пребывания заявки в системе
Средне число заявок под обслуживанием
Время пребывания заявки
в очередиСреднее число работающих ОУ в системе
LSIST=
(M/M/1/)
Слайд 27Пример расчета одноканальной СМО с неограниченной очередью
В порту имеется один
причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов
в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.Решение
Вероятность ожидания не более, чем 2-х судов
Слайд 34Литература
1. Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее
инженерные приложения. — Учеб. пособие для втузов. — 2-е
изд., стер.
— М.: Высш. шк., 2000. — 383 с:2. Клейнрок Л. Теория массового обслуживания. Пер. с англ. /Пер. И.И. Глушко; ред. В.И. Нейман. – М.: Машиностроение, 1979. – 432 с.
3/ Миллер Б. М., Панков А. Р. Теория случайных процеспроцессов в примерах и задачах. - М.: ФИЗМАТЛИТ, 2002. -320 с.