Слайд 1Основы автоматики и САУ
Часть 1
Слайд 2Технологические процессы (ТП) - целенаправленное преобразования вещества, энергии и информации
для получения требуемого продукта или результата.
В любом технологическом процессе выполняются
целенаправленные действия, называемые:
- рабочими операциями – создающими требуемый продукт или результат (например, перемещение груза роботом);
- вспомогательными операциями – создающими условия для нормального выполнения рабочих операций (например, захват и освобождение груза роботом);
- операциями управления рабочими и вспомогательными операциями во времени и в пространстве изменений координат системы.
Слайд 3Автоматикой называется отрасль науки и техники, охватывающая совокупность методов и
технических средств автоматического управления всеми операциями по осуществлению ТП в
технических объектах управления без непосредственного участия человека-оператора.
Термин «автоматика» образован от греческих слов «ауто» (сам) и «матос» (усиление, самоусиление, самодействие).
Слайд 4Системы автоматического управления (САУ) – это системы, в которых информация
о ходе технологического процесса используется для автоматического управления технологическим процессом
без участия человека, обеспечивая автоматизацию технологического процесса.
Слайд 5
В системах автоматического управления (САУ) все операции управления выполняются автоматическими
устройствами и поэтому САУ могут работать без участия человека.
В автоматизированных
системах управления (АСУ) часть операций управления выполняют автоматические устройства, а другую часть операций управления выполняет человек-оператор, без участия которого АСУ работать не могут.
Слайд 6Наука о методах и средствах автоматического управления техническими объектами управления
называется технической кибернетикой.
Методической основой технической кибернетики является теория автоматического
управления, которая оперирует математическими моделями элементов и САУ, рассматривает их информационные связи друг с другом и с окружающей средой и решает задачи анализа и синтеза САУ.
Слайд 7Анализ САУ заключается в определении и количественной оценке свойств САУ
с заданной структурой и известными параметрами элементов и внешних воздействий.
Синтез
САУ заключается в определении необходимой структуры и параметров элементов САУ для получения заданных свойств САУ при заданных воздействиях.
Слайд 9Классификация САУ
Разнообразие САУ по назначению, принципам построения, принципам действия, характеристикам,
способам получения и передачи информации и другим признакам исключает возможность
осуществления их всеобъемлющей классификации. Поэтому существует много частных классификаций САУ по разным групповым признакам.
Слайд 10 Классификация САУ
1) По виду уравнений, описывающих процессы управления:
а) класс
линейных систем управления;
б) класс нелинейных систем управления.
Слайд 11 Классификация САУ
Каждый класс систем управления делится на подклассы:
а) системы с
постоянными параметрами (описываются уравнениями с постоянными коэффициентами);
б) системы с переменными
параметрами (описываются уравнениями с переменными коэффициентами);
в) системы с распределенными параметрами (описываются уравнениями в частных производных);
г) системы с запаздыванием (описываются уравнениями с запаздывающим аргументом).
Слайд 12 Классификация САУ
2) По характеру передачи сигналов управления различают:
а) непрерывные (аналоговые)
системы управления;
б) дискретные системы управления (импульсные и цифровые);
в) релейные системы
управления.
Слайд 13 Классификация САУ
3) По характеру процессов в системе управления различают:
а) детерминированные
системы (имеют определенные параметры и определенные процессы);
б) стохастические системы (имеют
случайные параметры и случайные процессы).
Слайд 14 Классификация САУ
4) По характеру функционирования САУ делятся на четыре типа:
а)
обыкновенные САУ (имеют полную начальную информацию);
б) адаптивные САУ
(имеют неполную начальную информацию, автоматически восполняемую в процессе работы системы);
в) терминальные САУ (решают задачу достижения заданного состояния системы в конечный момент времени, до которого процесс управления может идти произвольно с оптимизацией по другим критериям);
г) интеллектуальные САУ – это САУ, способные к «пониманию» ситуации и обучению, в которых решаются задачи управления сложными ОУ с использованием механизма получения, хранения и системной обработки знаний (информации) об ОУ, возмущениях, состоянии внешней среды и условиях работы САУ для реализации своих функций управления на основе применения современных информационных технологий обработки знаний (информации) – искусственных нейронных сетей, нечеткой логики и других технологий.
Слайд 16ОСНОВЫ ТЕОРИИ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САУ
Математические модели САУ
Для математического описания САУ
по её функциональной схеме определяется состав её отдельных звеньев, связанных
друг с другом и с внешней средой.
Основными формами представления операторов преобразования входных переменных в переменные выхода в конечномерных линейных непрерывных стационарных детерминированных моделях звеньев и САУ являются:
дифференциальные уравнения,
передаточные функции,
временные и частотные характеристики .
Слайд 17Математические модели САУ
Происходящие в каждом звене процессы описываются линейными дифференциальными
уравнениями зависимости выходной величины у(t) от входного воздействия x(t).
где
m<=n для конструктивной реализации
Слайд 18Математические модели САУ
Эти уравнения называются математическими моделями звеньев и для
звеньев разной физической природы составляются по законам соответствующей науки (механики,
электротехники, термодинамики и др.), нелинейные уравнения линеаризуются.
Совокупность уравнений (математических моделей) взаимосвязанных звеньев САУ образуют систему уравнений САУ, называемую математической моделью САУ.
Слайд 19Передаточная функция или операторная функция передачи (ОФП) является важнейшим математическим
описанием звена или САУ, представляющим запись дифференциального уравнения в операторной
форме в виде отношения изображений по Лапласу выходной и входной величин при нулевых начальных условиях, которая получается в виде:
Слайд 20Операторная функция передачи (ОФП)
Переводим дифференциальное уравнение в операторную форму, заменой:
и далее
и далее
Слайд 21Операторная функция передачи (ОФП)
Получаем из дифференциального уравнения:
Уравнение в операторной
форме после замены:
Слайд 22Операторная функция передачи (ОФП)
Вынесем y(p) и x(p) за скобки:
Запишем
ОФП:
Слайд 23Типовые звенья САУ и их характеристики
Звенья с математическим описанием обыкновенными
дифференциальными уравнениями первого и второго порядка называются типовыми динамическими звеньями.
Из
типовых динамических звеньев составляются алгоритмические структурные схемы систем управления.
Знание характеристик типовых звеньев значительно облегчает изучение свойств таких систем.
Слайд 24Типовые звенья САУ и их характеристики
Классификацию типовых звеньев удобно осуществить,
рассматривая различные частные случаи общего дифференциального уравнения:
В операторной форме:
Слайд 25Типовые звенья САУ и их характеристики
Вынесем x(p) и y(p) за
скобки:
Передаточная функция в общем виде для типовых звеньев САУ:
Слайд 26Типовые звенья САУ и их характеристики
Принято уравнение:
записывать в виде (разделив
на ):
где
Параметры T2, T1, τ называются постоянными
времени, измеряемыми в секундах;
K называется коэффициентом передачи.
Слайд 27Типовые звенья САУ и их характеристики
Передаточная функция из уравнения:
в общем
виде для типовых звеньев САУ:
Слайд 28Типовые звенья САУ и их характеристики
Типовые динамические звенья делятся по
зависимостям выходной величины y от входного воздействия x в установившихся
режимах работы на:
позиционные, в которых выходная величина пропорциональна входному воздействию y=Kx;
интегрирующие, в которых выходная величина пропорциональна интегралу от входного воздействия y=K∫xdt;
дифференцирующие, в которых выходная величина пропорциональна дифференциалу (первой производной по времени) от входного воздействия y=K dx/dt;
запаздывающие, в которых выходная величина равна входной величине, сдвинутой в текущем времени на время запаздывания τ y=x(t – τ).
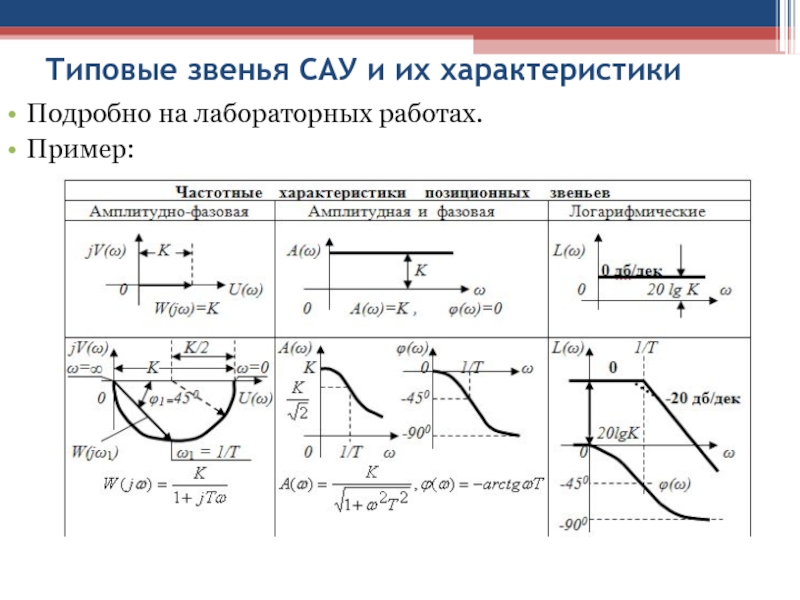
Слайд 29Типовые звенья САУ и их характеристики
Подробно на лабораторных работах.
Пример:
Слайд 30Типовые звенья САУ и их характеристики
Подробно на лабораторных работах.
Пример:
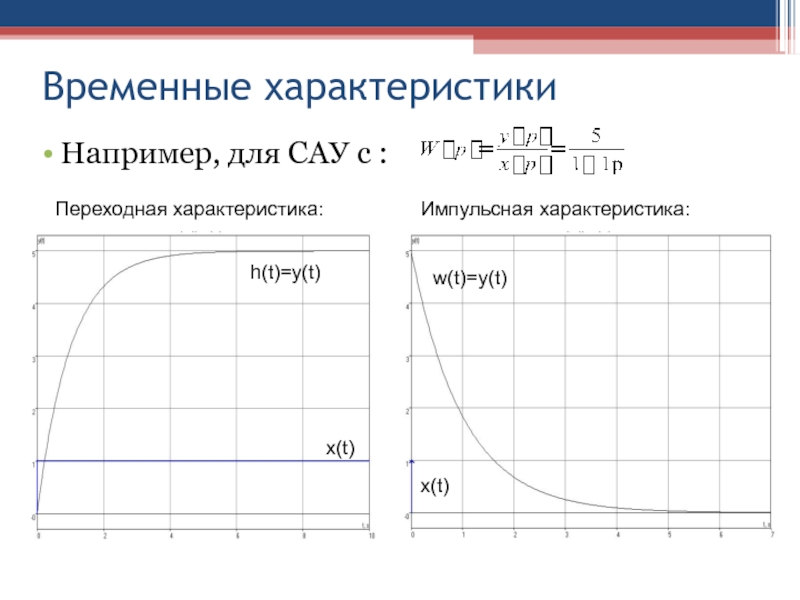
Слайд 31Временные характеристики
Временными характеристиками звена или САУ являются переходная функция h(t)
и функция веса w(t) .
Переходной функцией (переходной характеристикой) h(t)=y(t)
звена или САУ называется реакция на единичное ступенчатое входное воздействие x(t)=1[t] при нулевых начальных условиях.
Функцией веса (весовой функцией, импульсной переходной характеристикой) w(t)=y(t) звена или САУ называется реакция на единичное импульсное входное воздействие x(t)=δ(t) (дельта-функцию или функцию Дирака) при нулевых начальных условиях.
Слайд 32Временные характеристики
Дельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой
функции δ(t)=d1[t]/dt, при этом δ(t)=0 в любой момент времени t,
кроме t=0, где величина импульса стремится к бесконечности при бесконечно малой продолжительности импульса, а площадь импульса равна единице ∫δ(t)dt=1.
Функция веса w(t) связана с переходной функцией h(t) дифференцирования w(t)=dh(t)/dt.
Слайд 33Временные характеристики
Например, для САУ с :
Переходная характеристика:
Импульсная характеристика:
x(t)
x(t)
h(t)=y(t)
w(t)=y(t)
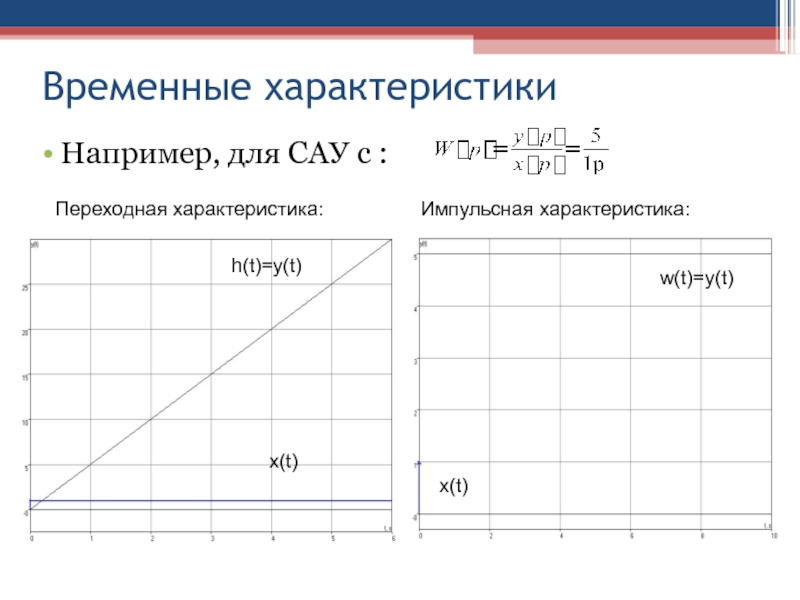
Слайд 34Временные характеристики
Например, для САУ с :
Переходная характеристика:
Импульсная характеристика:
x(t)
h(t)=y(t)
x(t)
w(t)=y(t)
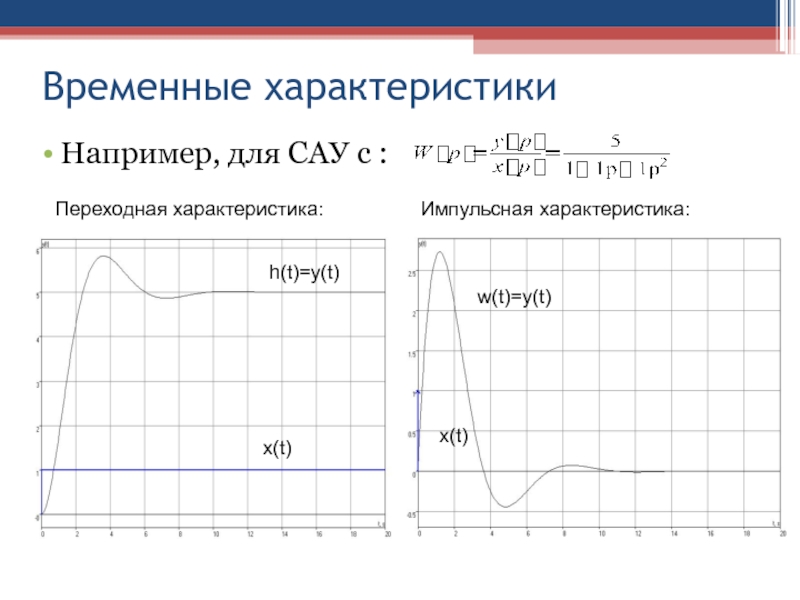
Слайд 35Временные характеристики
Например, для САУ с :
Переходная характеристика:
Импульсная характеристика:
x(t)
w(t)=y(t)
x(t)
h(t)=y(t)
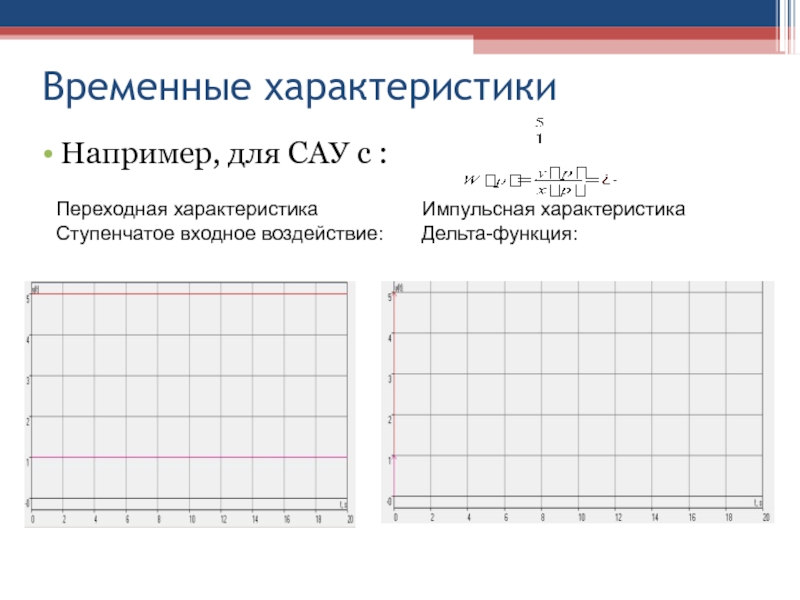
Слайд 36Временные характеристики
Например, для САУ с :
Переходная характеристика
Ступенчатое входное воздействие:
Импульсная характеристика
Дельта-функция:
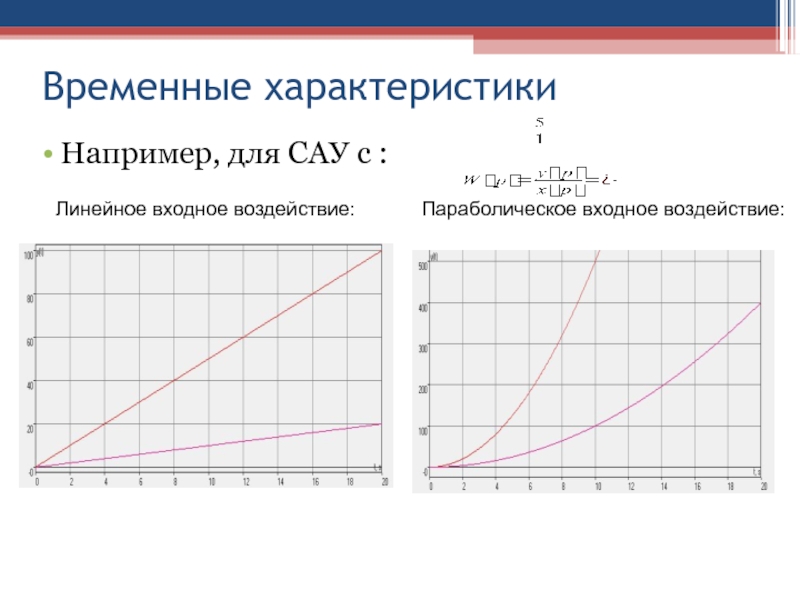
Слайд 37Временные характеристики
Например, для САУ с :
Линейное входное воздействие:
Параболическое входное воздействие:
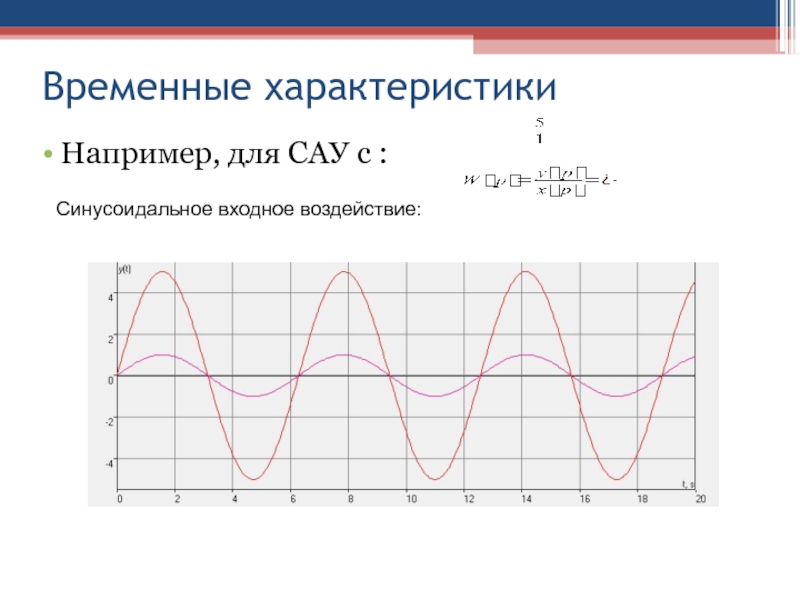
Слайд 38Временные характеристики
Например, для САУ с :
Синусоидальное входное воздействие:
Слайд 39Частотные характеристики
Частотные характеристики представляют собой зависимость амплитуды и фазы выходного
сигнала звена или системы в установившемся режиме при гармоническом входном
сигнале неизменной амплитуды и изменяемой частоты.
Частотные характеристики имеют важное значение для исследования систем автоматического управления, так как они характеризуют передаточные свойства звеньев и систем.
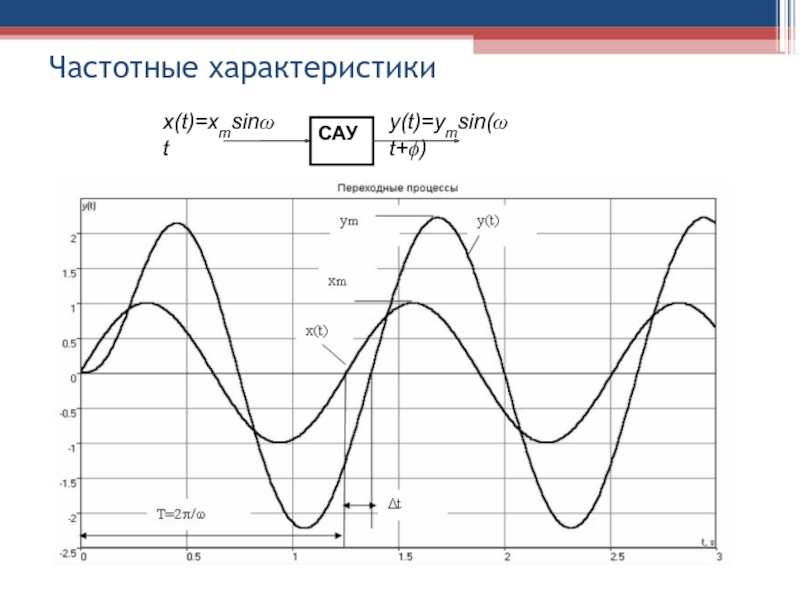
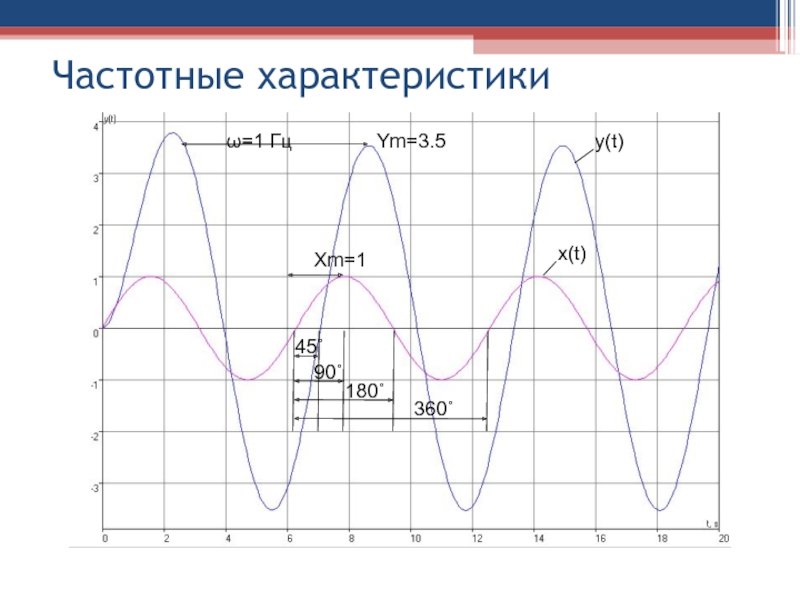
Слайд 40Частотные характеристики
Если на вход САУ в момент времени t=0 приложено
гармоническое воздействие x(t) определенной частоты ω:
x(t)=xmsinω t ,
то после окончания
переходного процесса в системе установится режим установившихся вынужденных колебаний, а выходная величина y(t) будет изменяться по гармоническому закону с той же частотой ω, но с другой амплитудой ym и со сдвигом Δt во времени:
y(t)=ym sin(ω t+ϕ),
где ϕ = (Δt /T) ⋅360 – фазовый сдвиг между входным и выходным сигналами в градусах.
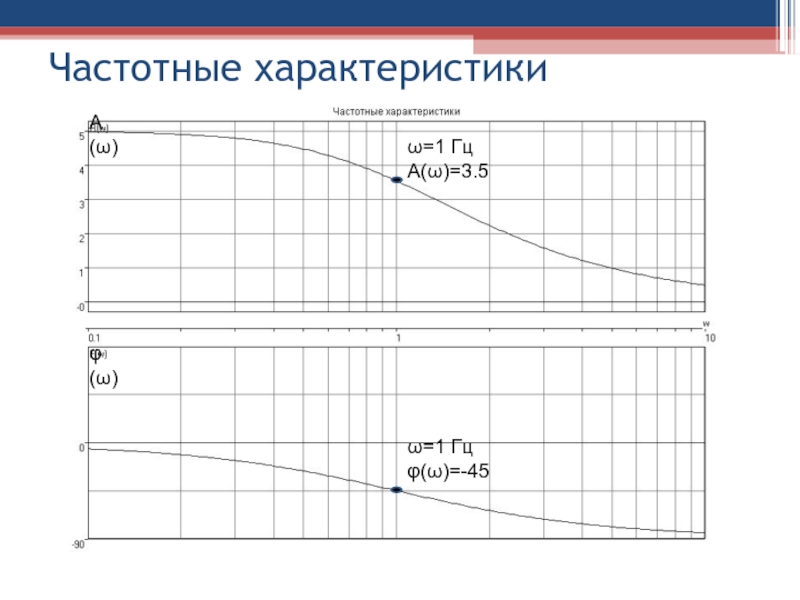
Слайд 42Частотные характеристики
Изменяя частоту ω от 0 до ∝ при
постоянном значении xm, можно установить, что амплитуда и фазовый сдвиг
выходного сигнала зависят от частоты входного сигнала.
Так как амплитуда выходного сигнала определяется также значением амплитуды входного сигнала, то возникает необходимость рассматривать отношение амплитуд ym /xm.
Слайд 43Частотные характеристики
Зависимость отношения амплитуд выходного и входного сигнала от
частоты называют амплитудной частотной характеристикой (АЧХ) и обозначают А(ω)
.
АЧХ характеризует пропускание элементом сигналов различной частоты. Пропускание оценивается по отношению амплитуд ym /xm.
Слайд 44Частотные характеристики
Зависимость фазового сдвига между входным и выходным сигналами от
частоты называют фазовой частотной характеристикой (ФЧХ) ϕ(ω).
Если фазовый сдвиг
то говорят о фазовом запаздывании, если фазовый сдвиг >0, то говорят о фазовом опережении.
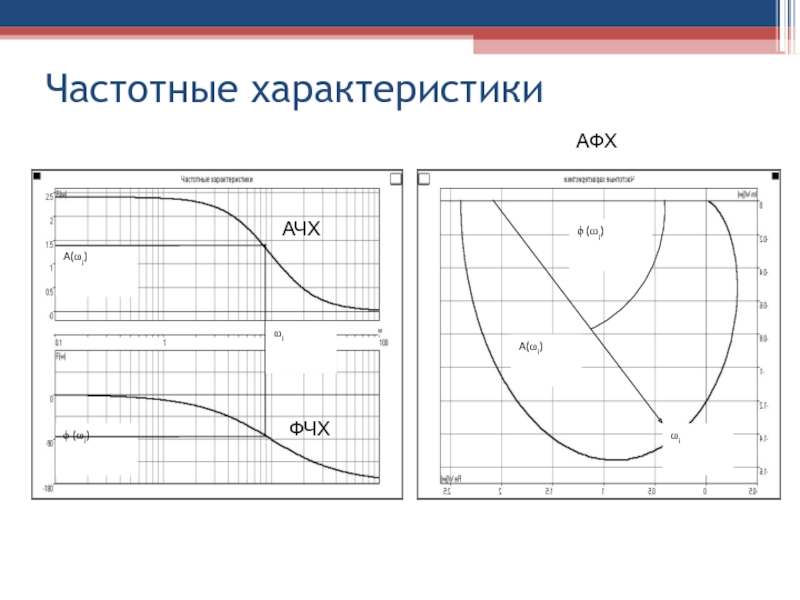
Слайд 47Частотные характеристики
При объединении амплитудной и фазовой частотных характеристик в одну
получают амплитудно-фазовую частотную характеристику (АФЧХ или АФХ) (частотная передаточная функция,
комплексный коэффициент передачи) W(jω), которая получается из передаточной функции (ОФП) W(p) звена или САУ при замене p=jω и изменении частоты ω от 0 до ∞.
Слайд 48Частотные характеристики
Амплитудно-фазовая частотная характеристика W(jω) является функцией комплексного переменного jω.
Модуль АФХ равен А(ω), а аргумент равен ϕ (ω).
Каждому значению
частоты ωi соответствует комплексное число W(jωi), представленное на комплексной плоскости изображающим вектором длиной A(ωi ) и расположенным к вещественной положительной оси под углом ϕ(ωi ).
Слайд 49Частотные характеристики
АФХ
АЧХ
ФЧХ
Слайд 51Частотные характеристики
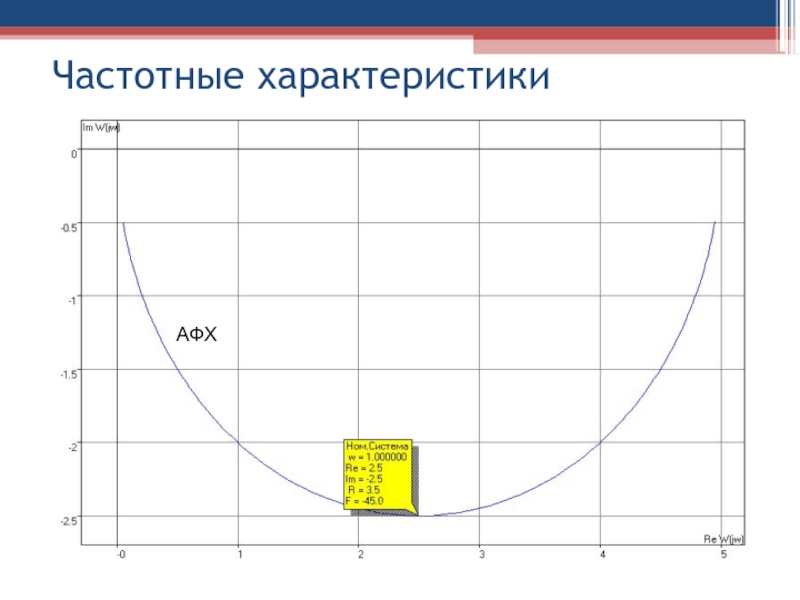
Выражение для амплитудно-фазовой характеристики конкретного элемента можно получить из
его передаточной функции подстановкой p=jω :
W(jω)=W(p) p=jω
АФХ W(jω) может
быть представлена в:
показательной форме:
W(jω) = A(ω)e jϕ(ω)
алгебраической:
W(jω) = U(ω) + jV(ω)
где U(ω), V(ω) –вещественная и мнимая составляющие вектора W(jω);
– амплитудная частотная характеристика (АЧХ);
ϕ(ω)=arc tg [V(ω)/U(ω)]– фазовая частотная характеристика (ФЧХ).
или тригонометрической:
Слайд 52Далее пример просто показать. Не под запись.
Слайд 53Частотные характеристики
Рассмотрим пример.
Пусть передаточная функция имеет вид:
Проведем замену:
Получаем:
Слайд 57Частотные характеристики
В расчетах САУ широко используются логарифмические частотные характеристики.
Логарифмическая
амплитудная частотная характеристика (ЛАЧХ) звена или САУ строится в прямоугольной
системе координат, где по оси ординат в линейном масштабе указывается величина ЛАЧХ в децибелах
L(ω)=20 lg⏐W(jω)⏐=20 lg A(ω),
а по оси абсцисс в логарифмическом масштабе указывается частота ω в 1/с (при этом равномерные изменения частоты в 10 раз представляются декадами).
Слайд 58Частотные характеристики
Децибел равен 1/10 бела.
Бел равен десятичному логарифму отношения мощностей
на выходе и входе звена или пропорциональному мощностям отношению квадратов
напряжений, токов, скоростей или других величин (1бел = lgP2/P1 = lgU22/U12).
Поэтому множитель 20=2∙10, где 2 отражает логарифмирование квадрата отношения выходной и входной величин, а 10 – перевод белов в децибелы.
Слайд 59Частотные характеристики
Логарифмическая фазовая частотная характеристика (ЛФЧХ) φ(ω)=arctg[V(ω)/U(ω)] звена или САУ
строится по оси ординат в линейном масштабе, где указывается угол
фазового сдвига ϕ(ω) в радианах или угловых градусах, а по оси абсцисс указывается частота ω в логарифмическом масштабе в 1/с.
Слайд 60Частотные характеристики
ω=1 Гц
L(ω)=20lg(3.5)= 10,88дБ
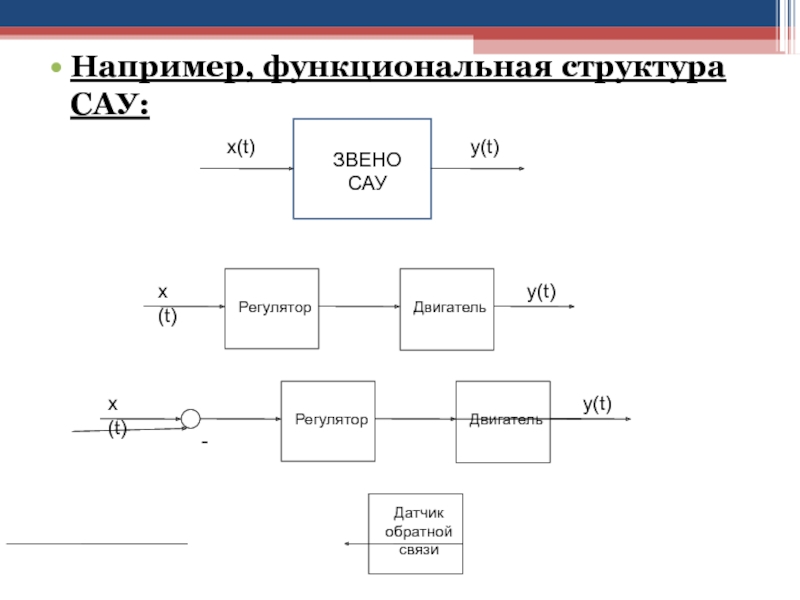
Слайд 65САУ представляется её функциональной, алгоритмической и конструктивной структурами (структурными схемами).
Слайд 66Функциональная структура САУ определяет состав функциональных блоков, выполняющих определённые функции:
получение текущей информации (датчики), формирование управляющего воздействия (регулятор) и т.д.
Каждый
функциональный блок изображается на схеме прямоугольником с соответствующим обозначением, а связи между блоками и с внешней средой обозначаются линиями со стрелкой, указывающей направление передачи воздействий.
Слайд 67Например, функциональная структура САУ:
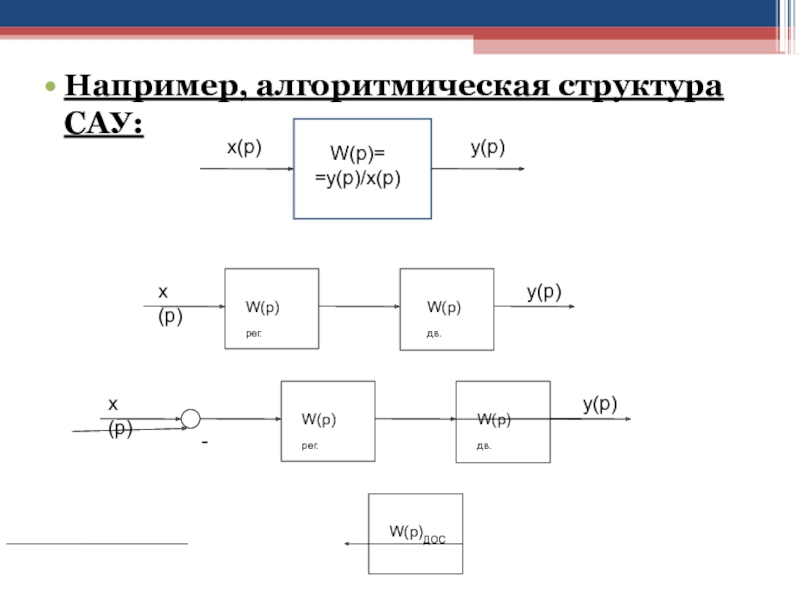
Слайд 68Алгоритмическая структура САУ представляет собой математическую модель САУ, состоящую из
однонаправленных звеньев и связей звеньев друг с другом и с
окружающей средой.
Каждое звено изображается прямоугольником, в котором записывается операторная функция передачи W(p) или её обозначение, приведенное в приложении.
Связи звеньев между собой и с внешней средой обозначаются линиями со стрелкой, указывающей направление передачи сигналов или физических воздействий.
Слайд 69Например, алгоритмическая структура САУ:
Слайд 70Конструктивная структура САУ определяет состав её конструктивных элементов и связей
их друг с другом и с внешней средой, которая представляется
графически в виде принципиальной конструктивной схемы с использованием стандартных изображений.
В системах электроавтоматики конструктивная структура представляется принципиальной электрической схемой из элементов и электрических цепей их соединений.
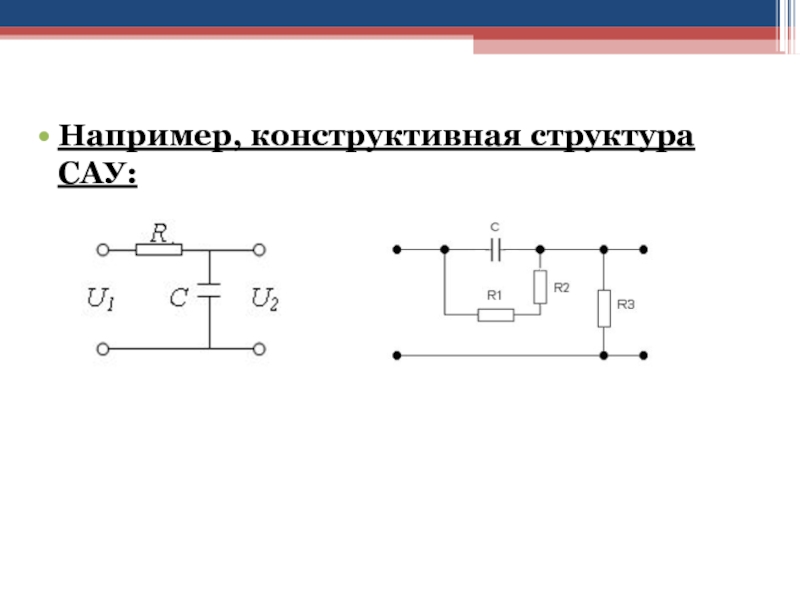
Слайд 71Например, конструктивная структура САУ:
Слайд 72Ниже пример того, как составляются
дифференциальные уравнения.
Слайд 73Математические модели САУ
Например:
Пусть дана схема:
Требуется составить дифференциальное уравнение электрической цепи:
Входной
величиной для цепи является напряжение U1, а выходной величиной –
напряжение U2.
В динамических режимах по одноконтурной цепи протекает ток i.
Слайд 74Математические модели САУ
Например:
Пусть дана схема:
На основании закона Кирхгофа при нулевых
начальных
условиях составим уравнение для
входного напряжения U1 :
U1 (t) =i(t)*R +
(1/C)*∫ i(t)dt (1)
Слайд 75Математические модели САУ
Например:
Пусть дана схема:
Выходное напряжение U2 :
U2(t)= (1/C)*∫ i(t)dt
(2)
Продифференцируем (2):
dU2(t)/dt= (1/C)i(t)
откуда определим значение тока:
i(t) = C*dU2(t)/dt (3)
Слайд 76Математические модели САУ
Например:
Пусть дана схема:
Подставим (3) в уравнение (1):
Уравнение (4)
– дифференциальное уравнение данной цепи (звена).
U1 (t) =i(t)*R +
(1/C)*∫ i(t)dt =
=(C*dU2(t)/dt ) *R + (1/C)*∫ (C*dU2(t)/dt ) dt =
= RC*dU2(t)/dt + U2(t) (4)
Слайд 77Ниже пример того, как составляются
ОФП.
Слайд 78Математические модели САУ
Например:
Пусть дана схема:
Ранее получили дифференциальное уравнение данной цепи
(звена):
Получаем (4) в операторной форме:
U1 (t) =RC*dU2(t)/dt + U2(t)
(4)
Переводим дифференциальное уравнение в операторную форму, заменой:
U1 (p) =RC*U2(p)*p + U2(p)= U2(p)(1+RC*p) (5)
Слайд 79Математические модели САУ
Например:
Пусть дана схема:
Запишем согласно (5) ОФП:
U1 (p)
=RC*U2(p)*p + U2(p)= U2(p)(1+RC*p) (5)
Слайд 80Математические модели САУ
Например:
Пусть дана схема:
Пусть R=20кОм, С=5мкФ.
Тогда ОФП:
Слайд 81
Рассмотрим методику получения временных и частотных характеристик на примере апериодического
(инерционного) звена первого порядка имеющего передаточную функцию:
где T – постоянная времени звена; K – коэффициент передачи звена.
Дифференциальное уравнение процесса управления:
Слайд 82Например:
Пусть дана схема:
Дифференциальное уравнение процесса управления :
Слайд 83
Переходная функция звена h(t)=y(t)=U2(t) получается в виде суммы общего и
частного решений дифференциального уравнения при нулевых начальных условиях и подаче
на вход единичного ступенчатого воздействия x(t)=U1(t)=1[t].
Слайд 84
Частное решение получается из дифференциального уравнения
при
в виде:
Общее решение записывается в
виде:
где С – постоянная интегрирования, p – корень характеристического уравнения (знаменатель W(p)).
Слайд 85Найдем корень характеристического уравнения:
Где характеристическое уравнение:
Приравняем D(p)=0 и выразим
p = -10
Получаем:
Постоянную интегрирования С определим из
при подстановке
полного решения
и нулевых начальных условиях при t=0 и U2(t)=0
Слайд 86Получим:
Выполнив дифференцирование произведения функций С и
получим:
Слайд 87При подстановке нулевых начальных условиях при t=0 и U2(t)=0 получаем
из
Проинтегрируем полученное выражение и получим значение для постоянной интегрирования:
В результате
переходная функция имеет вид:
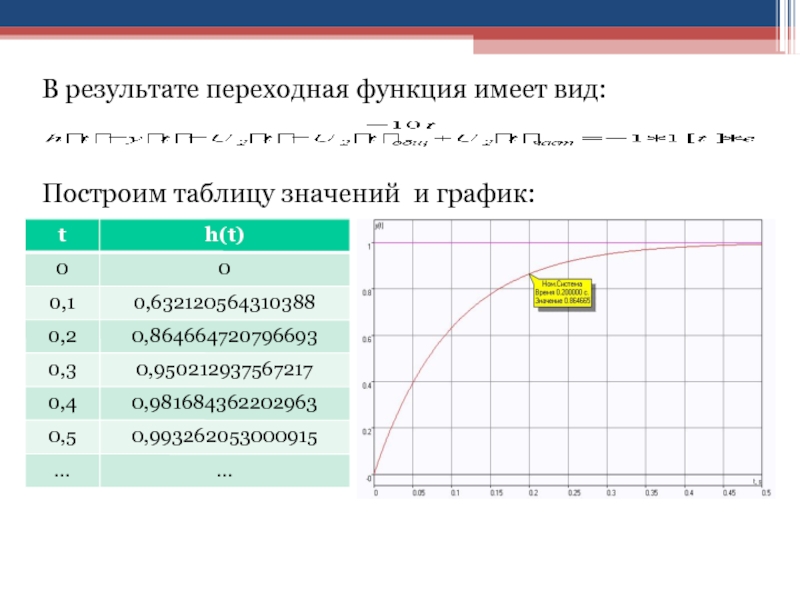
Слайд 88В результате переходная функция имеет вид:
Построим таблицу значений и график:
Слайд 89Типовые звенья САУ и их характеристики
Весовая функция определяется дифференцированием
h(t)
по времени:
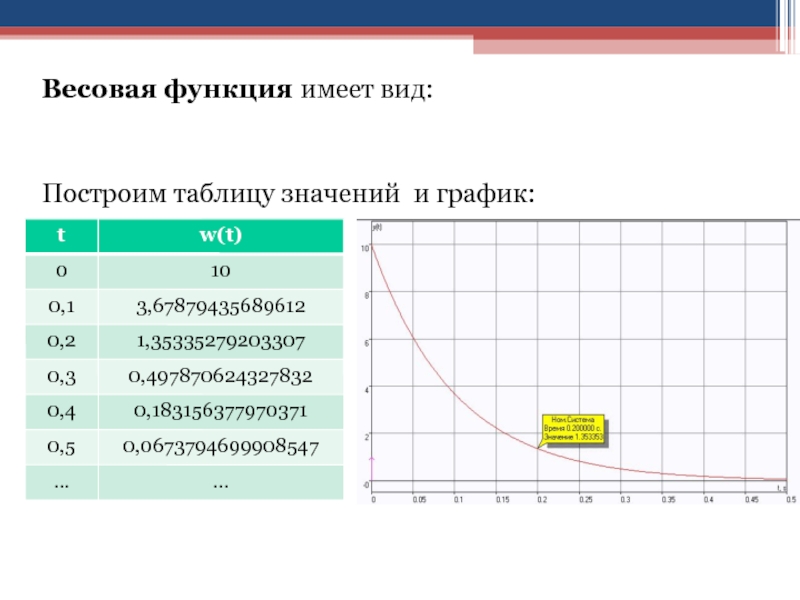
Слайд 90Весовая функция имеет вид:
Построим таблицу значений и график:
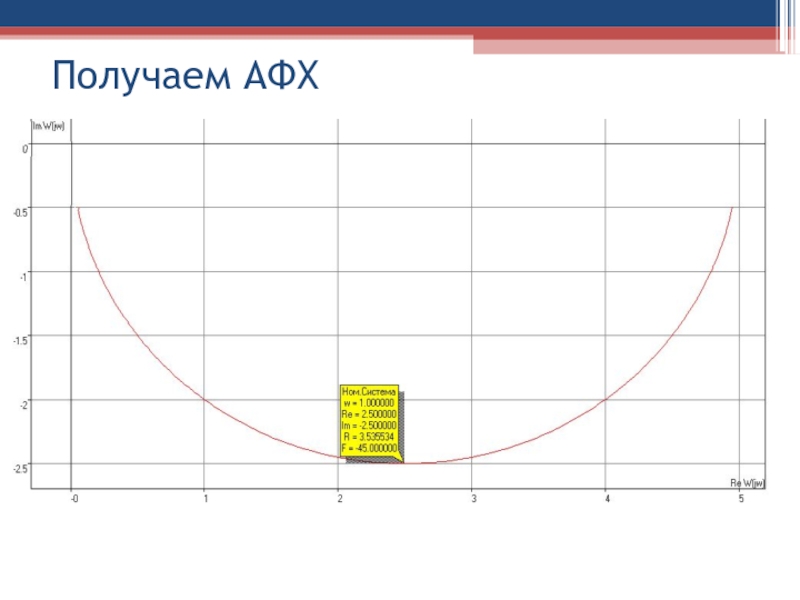
Слайд 91Частотная амплитудно-фазовая характеристика (АФХ) из уравнения ОФП:
при p=jω:
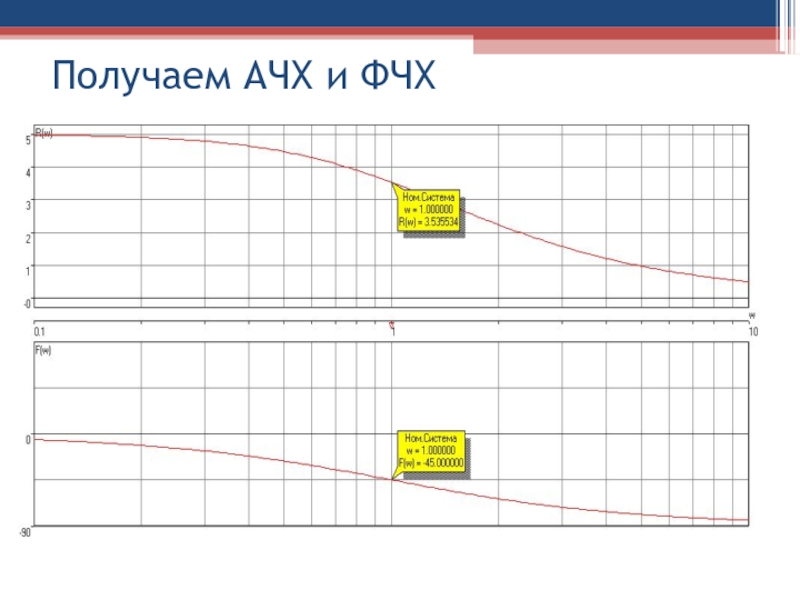
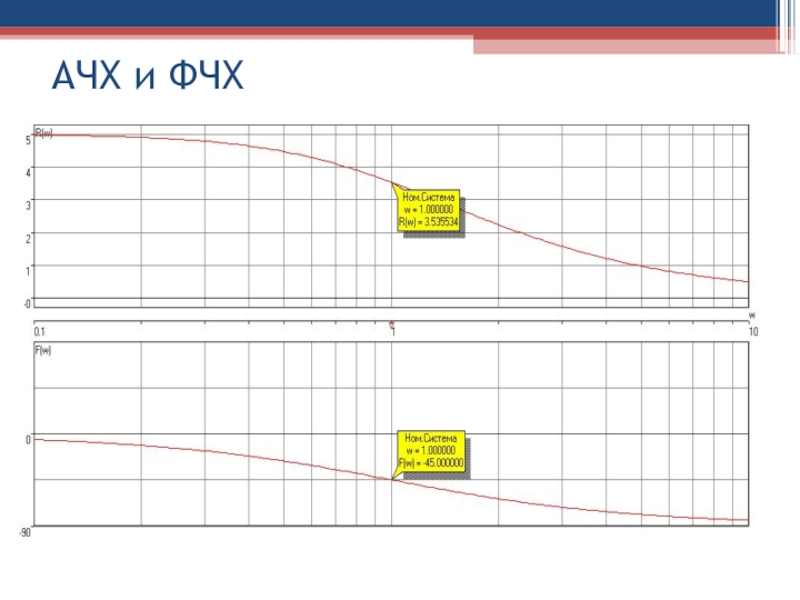
Слайд 92Амплитудная А(ω) и фазовая φ(ω) частотные характеристики (АЧХ и ФЧХ)
определяются из:
и имеют вид:
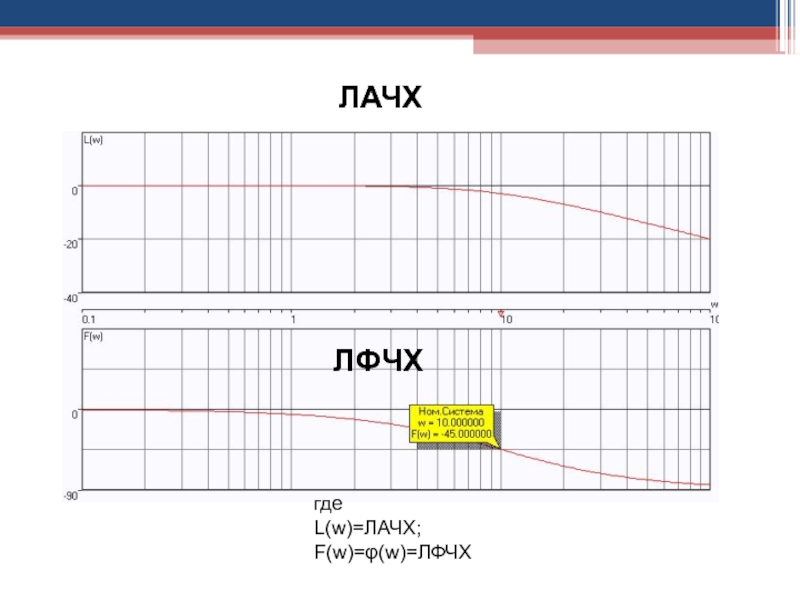
Слайд 93Логарифмическая амплитудная частотная характеристика (ЛАЧХ) описывается выражением:
Слайд 94Логарифмическая фазовая частотная характеристика (ЛФЧХ) звена имеет такое же расчетное
выражение как и ФЧХ, но строится совместно с ЛАЧХ этого
звена в логарифмическом масштабе частот и в линейном масштабе угла фазового сдвига, измеряемого в радианах или угловых градусах.
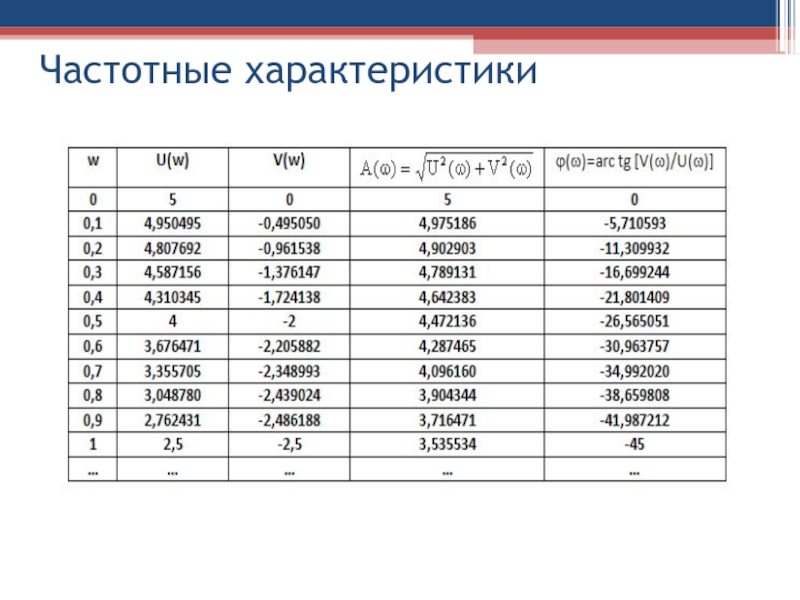
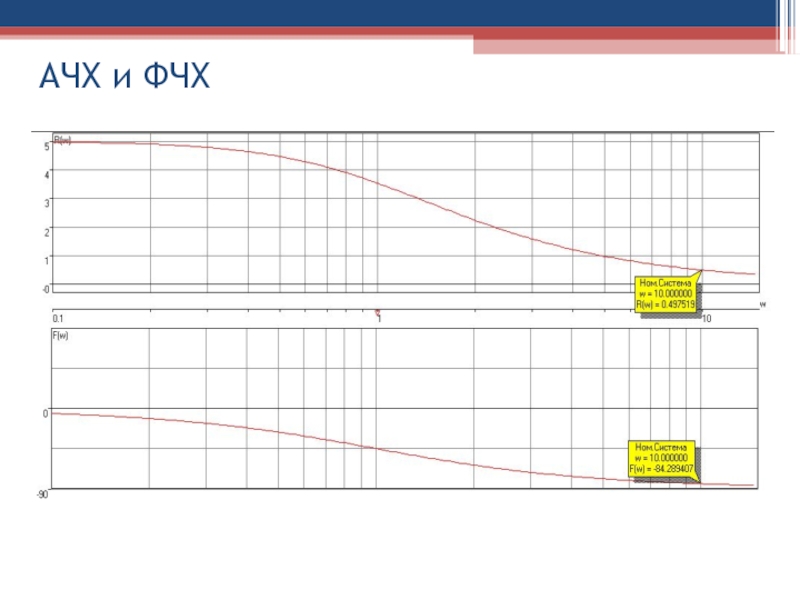
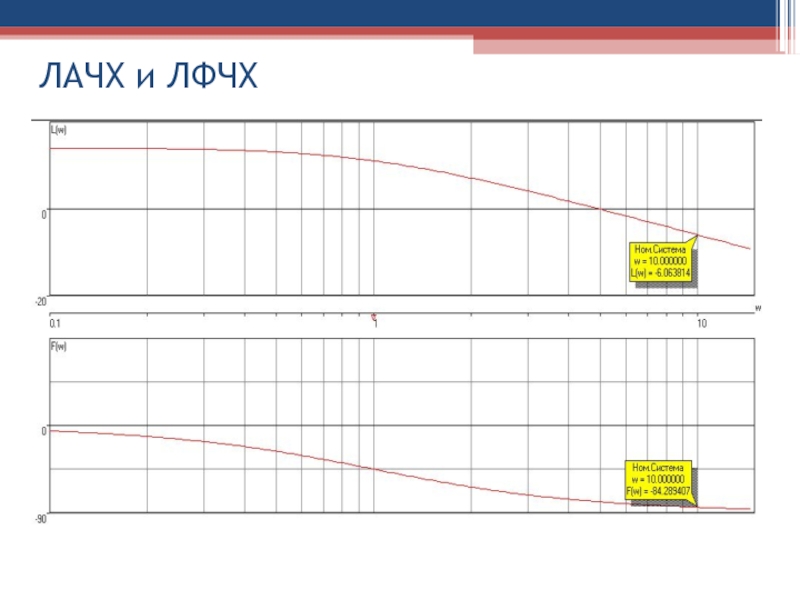
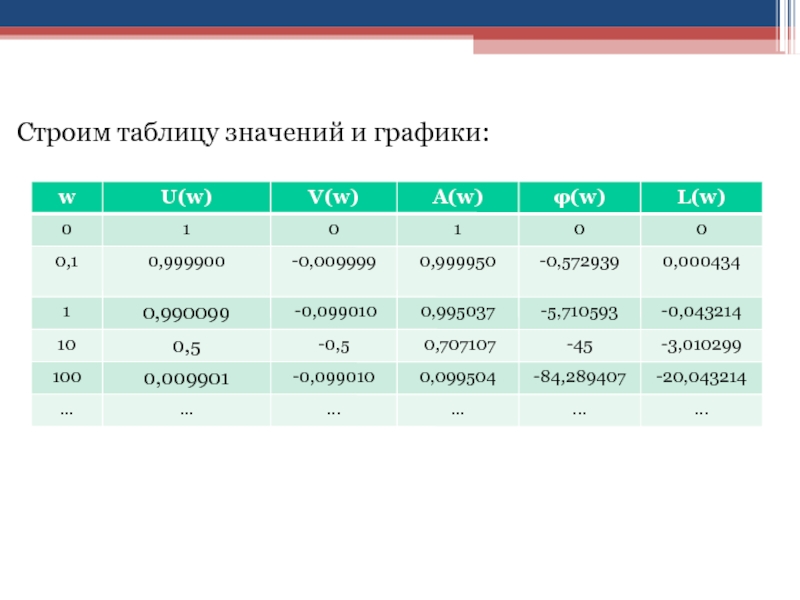
Слайд 95Строим таблицу значений и графики:
Слайд 96где
Re(w)=U(w);
Im(w)=V(w);
R(w)=A(w)=АЧХ;
F(w)=φ(w)=ФЧХ
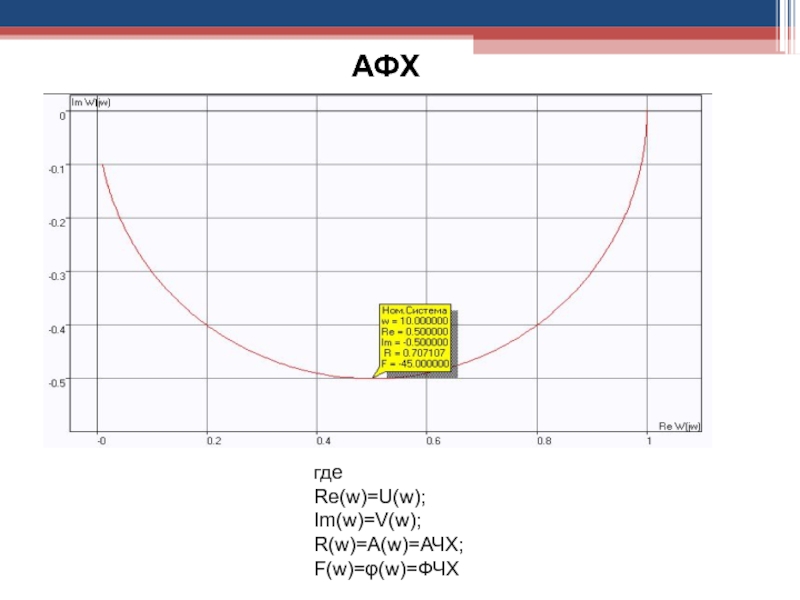
АФХ
Слайд 97где
R(w)=A(w)=АЧХ;
F(w)=φ(w)=ФЧХ
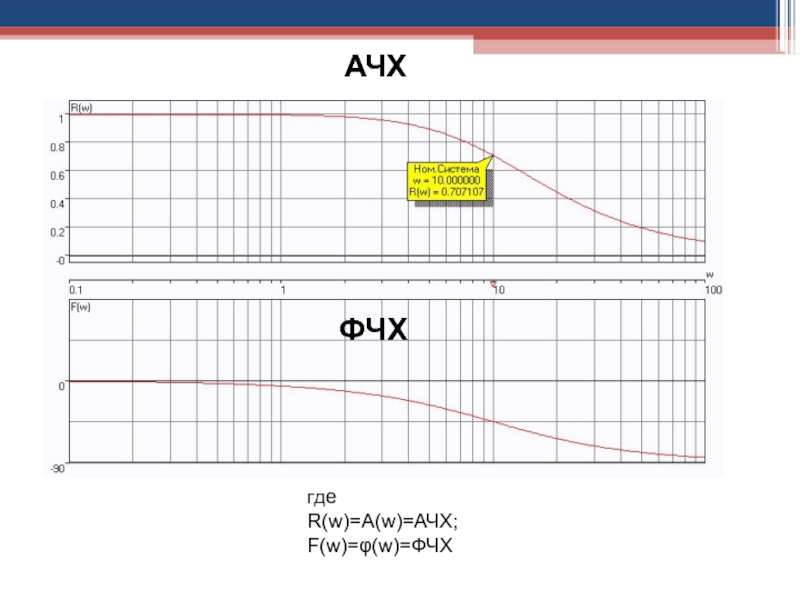
АЧХ
ФЧХ
Слайд 98где
R(w)=A(w)=АЧХ;
F(w)=φ(w)=ФЧХ
АЧХ
ФЧХ
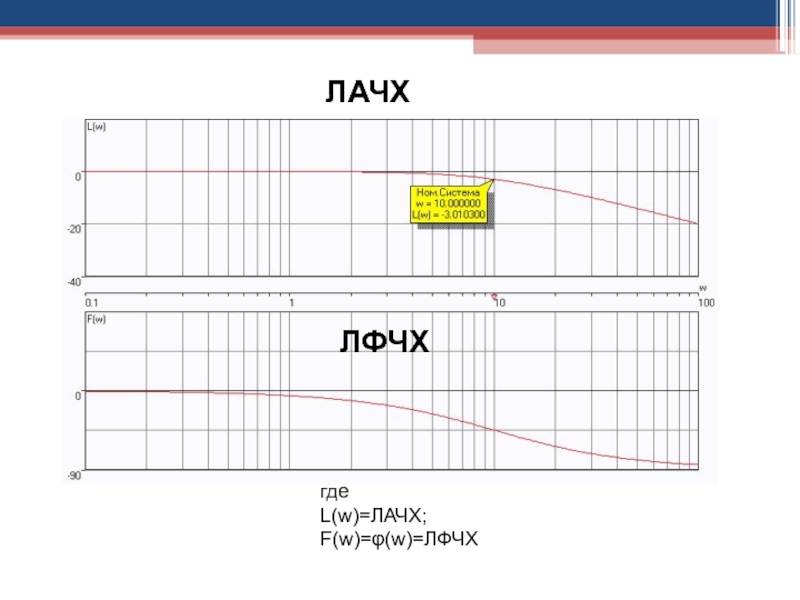
Слайд 99где
L(w)=ЛАЧХ;
F(w)=φ(w)=ЛФЧХ
ЛАЧХ
ЛФЧХ
Слайд 101 Для описания модели САУ обычно используется три способа:
1) поэлементное описание
САУ с учётом взаимодействия каждого звена с другими звеньями и
с внешней средой. При этом модель САУ описывается системой дифференциальных уравнений, учитывающих все параметры звеньев, входные и выходные величины (координаты) процессов управления, что обеспечивает возможность физической интерпретации всех процессов управления;
Слайд 102 Для описания модели САУ обычно используется три способа:
2) системное описание
САУ представляется одним уравнением, которое получается из поэлементного описания САУ
методом подстановок для исключения промежуточных координат процесса управления и учитывает только зависимость выходного процесса (выходной величины) САУ от входного процесса (входной величины) при утрате возможностей физической интерпретации процессов управления, происходящих внутри САУ;
Слайд 103 Для описания модели САУ обычно используется три способа:
3) векторно-матричное описание
САУ в пространстве переменных состояния системы, позволяющее учитывать все параметры
и переменные величины (координаты) САУ и вести расчёты с применением ЭВМ при возможности физической интерпретации происходящих процессов управления в САУ.
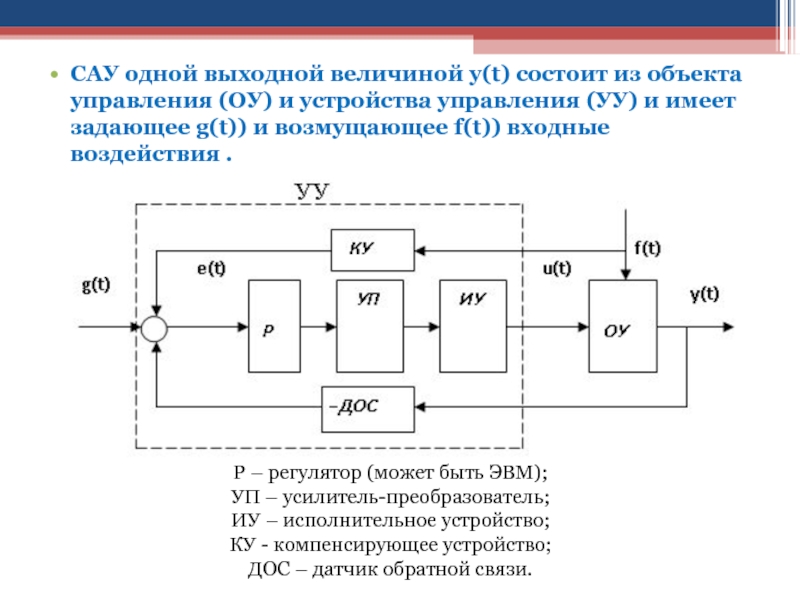
Слайд 104САУ одной выходной величиной y(t) состоит из объекта управления (ОУ)
и устройства управления (УУ) и имеет задающее g(t)) и возмущающее
f(t)) входные воздействия .
Р – регулятор (может быть ЭВМ);
УП – усилитель-преобразователь;
ИУ – исполнительное устройство;
КУ - компенсирующее устройство;
ДОС – датчик обратной связи.
Слайд 105Устройство управления (УУ) выполняет целенаправленные операции управления технологическим процессом (ТП),
формируя управляющее воздействие u(t) на ОУ по определенному закону –
алгоритму управления ОУ для достижения цели управления – обеспечения равенства y(t)=g(t) или допустимой ошибки управления g(t)–y(t)≤e(t)доп при наличии возмущающих воздействий f(t), отклоняющих y(t) от заданного значения g(t).
Слайд 106Объект управления (ОУ) в САУ выполняет рабочие операции осуществления ТП.
Для
этого выходной величиной y(t) ОУ необходимо управлять по заданному закону
g(t) – алгоритму функционирования ОУ и всей САУ за счет формирования управляющего воздействия u(t) на ОУ для достижения цели управления – равенства y(t)=g(t).
Слайд 107В устройстве управления (УУ) алгоритм управления формируется в регуляторе (Р),
который обычно реализуется с использованием операционных усилителей или микроЭВМ.
Для усиления
сигнала от регулятора Р в УУ вводятся усилитель–преобразователь (УП) и исполнительное устройство (ИУ) (например, электродвигатель), непосредственно воздействующее на объект управления (ОУ).
УУ в целом выполняет функции регулятора по отношению к объекту управления ОУ.
Слайд 108УУ могут строиться по трем основным принципам управления:
1) принцип разомкнутого
управления u(t)=K∙g(t) позволяет строить устойчивые разомкнутые САУ, имеющие самую низкую
точность управления из-за влияния возмущений f(t);
Слайд 109УУ могут строиться по трем основным принципам управления:
2) принцип компенсации
возмущающего воздействия f(t) (управление по возмущению) с введением компенсирующего устройства
КУ, добавляющего к задающему сигналу g(t) противодействующую составляющую влияния возмущения f(t) на выходную величину y(t), позволяет строить устойчивые разомкнутые САУ с уменьшенным влиянием f(t) на y(t);
Слайд 110УУ могут строиться по трем основным принципам управления:
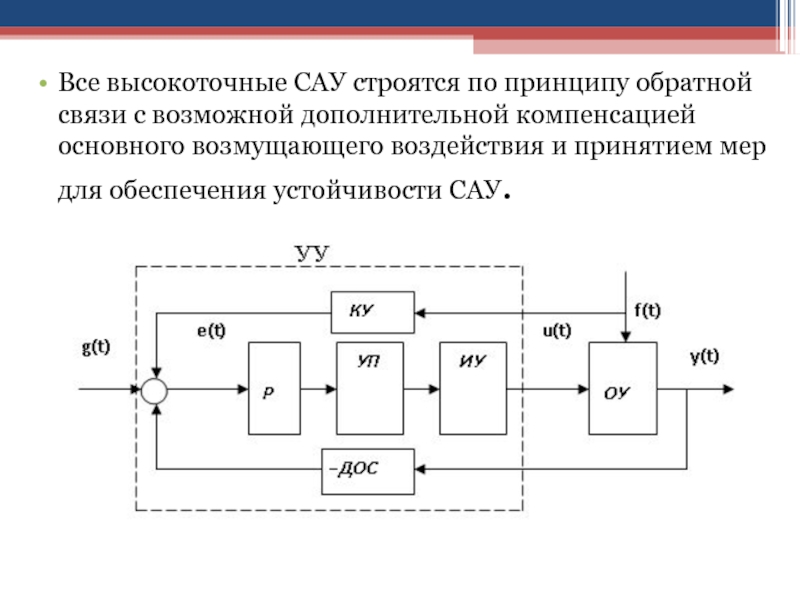
3) принцип обратной
связи (принцип отклонения, управление по ошибке) с введением в САУ
датчика обратной связи ДОС позволяет создавать замкнутые САУ, обеспечивающие высокую точность управления выходной величиной y(t) при полной или частичной компенсации ошибки управления е(t)=g(t)–y(t), независимо от причин её возникновения.
Слайд 111Все высокоточные САУ строятся по принципу обратной связи с возможной
дополнительной компенсацией основного возмущающего воздействия и принятием мер для обеспечения
устойчивости САУ.
Слайд 112В УУ часто используются линейные алгоритмы управления:
- пропорциональный u(t)=K∙e(t),
- интегральный
u(t)=K∫e(t)dt,
- пропорционально–интегральный u(t)=K[e(t)+∫e(t)dt],
- пропорционально–дифференциальный u(t)=K[e(t)+de(t)/dt],
- пропорционально–интегрально–дифференциальный u(t)=K[e(t)+∫e(t)dt+de(t)/dt].






























![Основы автоматики и САУ Временные характеристикиДельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой функции Временные характеристикиДельта-функция или функция Дирака получается при дифференцировании единичной ступенчатой функции δ(t)=d1[t]/dt, при этом δ(t)=0 в любой](/img/thumbs/1679f5a80369d5c404fd4675299723d1-800x.jpg)












![Основы автоматики и САУ Частотные характеристикиЛогарифмическая фазовая частотная характеристика (ЛФЧХ) φ(ω)=arctg[V(ω)/U(ω)] звена или САУ строится Частотные характеристикиЛогарифмическая фазовая частотная характеристика (ЛФЧХ) φ(ω)=arctg[V(ω)/U(ω)] звена или САУ строится по оси ординат в линейном масштабе,](/img/thumbs/c7268392adfa7588cf20152b31487e05-800x.jpg)




































![Основы автоматики и САУ В УУ часто используются линейные алгоритмы управления:- пропорциональный u(t)=K∙e(t),- интегральный u(t)=K∫e(t)dt,- В УУ часто используются линейные алгоритмы управления:- пропорциональный u(t)=K∙e(t),- интегральный u(t)=K∫e(t)dt,- пропорционально–интегральный u(t)=K[e(t)+∫e(t)dt],- пропорционально–дифференциальный u(t)=K[e(t)+de(t)/dt],- пропорционально–интегрально–дифференциальный u(t)=K[e(t)+∫e(t)dt+de(t)/dt].](/img/thumbs/48a033d7fbe9f00e4552290959a83255-800x.jpg)




















