Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы информационных технологий
Содержание
- 1. Основы информационных технологий
- 2. 08/13/2019Литература Калиткин Н.Н. Численные методы. – М:
- 3. 08/13/2019Метод и его погрешностьПри построении вычислительного алгоритма
- 4. 08/13/2019Порядок погрешности метода (продолжение)Обычно при уменьшении некоторого
- 5. 08/13/2019Из математической физикиМатематической моделью поля является функция нескольких переменных, обычноОператоры дифференцирования:
- 6. 08/13/2019Операторы дифференцированияТеорема Остроградского – Гаусса
- 7. 08/13/2019Обыкновенные ДУСистема ОДУ первого порядка
- 8. 08/13/2019Задача Кошиuxau0b
- 9. 08/13/2019Краевая задачаУсловия заданы на обоих концах отрезка
- 10. 08/13/2019ДУ в частных производных (ДУЧП)- параболические- гиперболические- эллиптические
- 11. 08/13/2019Граничные условияОбщее решение ДУЧП содержит произвольные дифференцируемые
- 12. 08/13/2019Суть метода сетокСуть метода сеток в том,
- 13. 08/13/2019Результат решения по методу сетокxb0αuβxb0αuβxiuiИскомое решениеРешение в виде таблицы
- 14. 08/13/2019Получение конечноразностной схемыРешение u(x) ищется в виде
- 15. 08/13/2019Конечно-разностная схема
- 16. 08/13/2019система конечно-разностных уравненийСтандартная система с трехдиагональной матрицей:
- 17. 08/13/2019Погрешность аппроксимацииПри замене дифференциального уравнения системой алгебраических
- 18. 08/13/2019Оценка погрешности решения Понятие устойчивостиПогрешность решения :Для
- 19. 08/13/2019Проекционные методы решения краевых задач- Краевая задача - базис из функций- Представление решения- Проекционное уравнение
- 20. 08/13/2019Решение одномерной краевой задачи методом ГалеркинаНайти решениеИщем решение в видеПроекционное уравнениепреобразуем
- 21. 08/13/2019Решение одномерной краевой задачи (продолжение1)Подставляем uNПреобразуем и
- 22. 08/13/2019Базис из финитных функцийФинитной называется функция
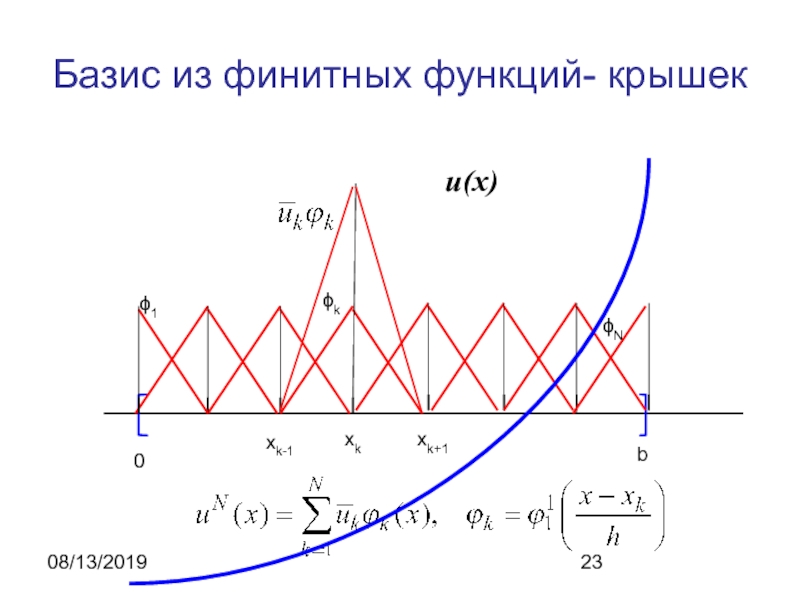
- 23. 08/13/2019Базис из финитных функций- крышек
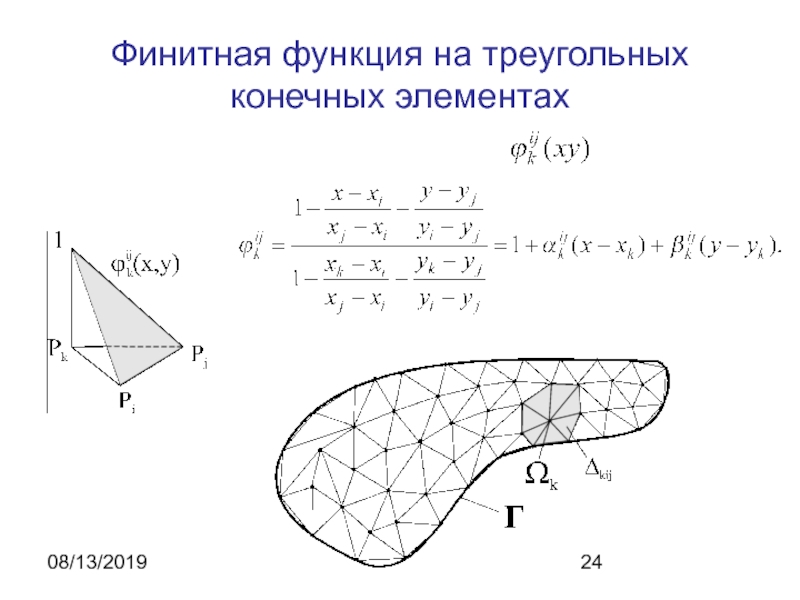
- 24. 08/13/2019Финитная функция на треугольных конечных элементах
- 25. 08/13/2019Базисные финитные функции
- 26. Скачать презентанцию
08/13/2019Литература Калиткин Н.Н. Численные методы. – М: Наука, 1978. Болсун А.И., Гронский В.К., Бейда А.А. Методы математической физики. – Мн.: Выш. Шк., 1988.Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. –
Слайды и текст этой презентации
Слайд 108/13/2019
Курс Основы информационных технологий
Раздел
Проекционно-сеточные методы решения уравнений математической физики
(установочная
лекция)
(а. 412 – 5к)Слайд 208/13/2019
Литература
Калиткин Н.Н. Численные методы. – М: Наука, 1978.
Болсун
А.И., Гронский В.К., Бейда А.А. Методы математической физики. – Мн.:
Выш. Шк., 1988.Марчук Г.И., Агошков В.И. Введение в проекционно-сеточные методы. – М.: Наука, 1981.
Банди Б. Методы оптимизации. Вводный курс. – М.: Радио и связь, 1988.
Марчук Г.И. Методы вычислительной математики. – М.: - Наука, 1980.
Синицын А.К. Современные информационные технологии. Проекционно-сеточные методы решения уравнений математической физики. Конспект лекций для аспирантов и магистрантов Мн.: БГУИР, 2004.
Синицын А.К. ,Навроцкий А.А. Алгоритмы вычислительной математики. Учебно-методическое пособие. Мн.: БГУИР, 2007
Слайд 308/13/2019
Метод и его погрешность
При построении вычислительного алгоритма обычно точное решение
некоторой задачи
A(Y)=b
Y=F(x)представляется в виде бесконечного предела последовательности арифметических и логических действий:
Yh=Mh(x)
Mh – метод, h – параметр метода
При ограничении лишь конечным числом вычислений вносится контролируемая параметром h метода погрешность
ε(h)=Y-Yh
Получение зависимости погрешности решения ε(h) от параметров вычислительного метода является одной из основных задач вычислительной математики
Слайд 408/13/2019
Порядок погрешности метода (продолжение)
Обычно при уменьшении некоторого параметра h метода
погрешность решения εh стремится к нулю, т.е.
при
В этом случае, если удается получить оценку вида
где С - const и не зависит от h, считается, что порядок погрешности равен p и обозначается коротко
Слайд 508/13/2019
Из математической физики
Математической моделью поля является функция нескольких переменных, обычно
Операторы
дифференцирования:
Слайд 908/13/2019
Краевая задача
Условия заданы на обоих концах отрезка [a,b].
Эта задача
обычно ставится для ДУ второго порядка
В общем случае
Слайд 1108/13/2019
Граничные условия
Общее решение ДУЧП содержит произвольные дифференцируемые функции, например
Решением
является
Начальные условия
Граничные условия
первого рода второго рода третьего рода
Дирихле Неймана Ньютона
Слайд 1208/13/2019
Суть метода сеток
Суть метода сеток в том, что решение ДУ
получают в виде достаточно подробной таблицы значений искомого решения в
узлах сетки, покрывающей область определения решения.Получаемая таблица должна обладать свойством аппроксимации, т.е. возможностью восстановления всех значений искомого точного решения с заданной погрешностью.
Будем иллюстрировать реализацию метода сеток на решении простейшей одномерной краевой задачи Дирихле
В общем случае
Г - граница многомерной области Ω, внутри которой необходимо получить решение. В рассматриваемом частном случае Ω представляет собой отрезок
Слайд 1308/13/2019
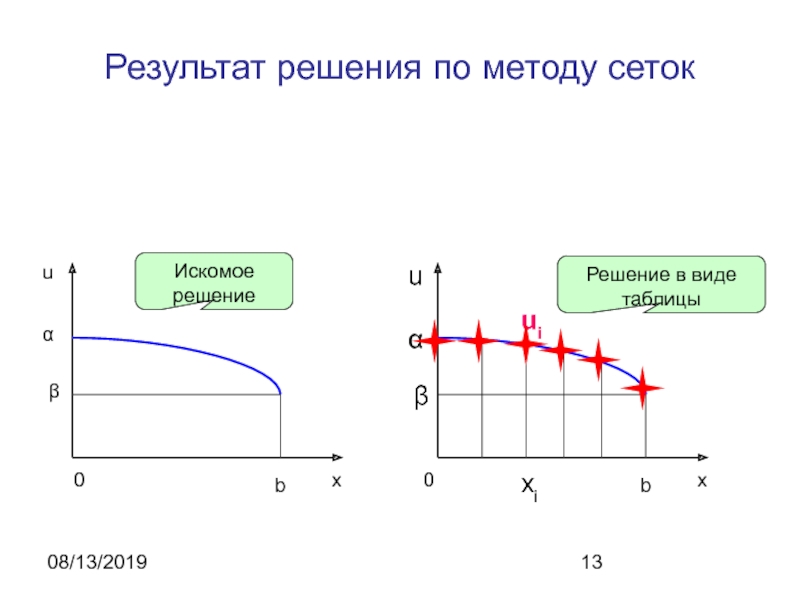
Результат решения по методу сеток
x
b
0
α
u
β
x
b
0
α
u
β
xi
ui
Искомое решение
Решение в виде таблицы
Слайд 1408/13/2019
Получение конечноразностной схемы
Решение u(x) ищется в виде таблицы значений в
узлах выбранной сетки
дифференциальное уравнение
заменяется системой алгебраических уравнений, связывающих между собой значения искомой функции в соседних узлах. Такая система алгебраических уравнений называется конечно-разностной схемой
Обозначим
Имеется много способов получения конечно-разностной схемы
Слайд 1608/13/2019
система конечно-разностных уравнений
Стандартная система с трехдиагональной матрицей:
Слайд 1708/13/2019
Погрешность аппроксимации
При замене дифференциального уравнения системой алгебраических уравнений вносится так
называемая погрешность аппроксимации конечно-разностной схемой дифференциального уравнения
подставим в конечно-разностную схему
вместо значения точного решения . Ввиду того, что , после такой подстановки получается невязка
Погрешность аппроксимации
Основное требование: при
Ассимптотическая оценка
Порядок погрешности аппроксимации = p
Слайд 1808/13/2019
Оценка погрешности решения Понятие устойчивости
Погрешность решения :
Для сходимости к точному
решению
кроме
необходимаустойчивость к ошибкам округления
Основная теорема








![Основы информационных технологий 08/13/2019Краевая задачаУсловия заданы на обоих концах отрезка [a,b]. Эта задача обычно 08/13/2019Краевая задачаУсловия заданы на обоих концах отрезка [a,b]. Эта задача обычно ставится для ДУ второго порядкаВ общем](/img/thumbs/25f85dc912f1e1ae0e7b918fff64425e-800x.jpg)