Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы информатики _ Основные понятия и определения.pptx
Содержание
- 1. Основы информатики _ Основные понятия и определения.pptx
- 2. Термин "информация" происходит от латинского слова "Informatio" – разъяснение, изложение, осведомленность.ИнформацияДанныеЗнанияОпределение информации
- 3. Свойства информацииРелевантностьПолнотаСвоевременность (актуальность)ДостоверностьДоступностьЗащищенностьЭргономичностьАдекватность
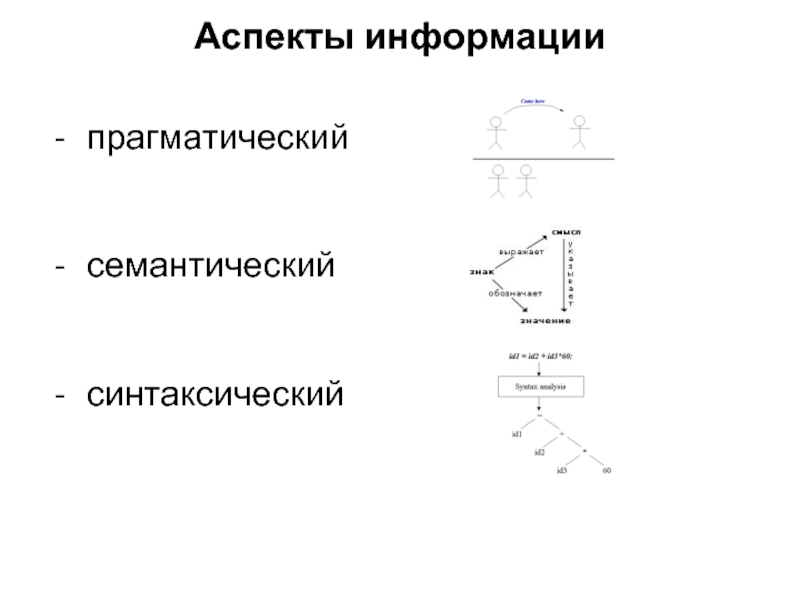
- 4. Аспекты информациипрагматическийсемантический синтаксический
- 5. Тезаурус Семантические связи между словами или другими смысловыми
- 6. Структурная мера информацииЭлементарная единицы сообщений – символСимволы,
- 7. Структурная мера информацииГеометрическая мера предполагает измерение параметра
- 8. Структурная мера информацииАддитивная мера (мера Хартли), в
- 9. Структурная мера информацииПри заданных глубине и длине
- 10. Структурная мера информацииКоличество информации при этом эквивалентно
- 11. Статистическая мера информацииЭнтропия – количественная мера неопределенности и, следовательно, информативности.Иными словами, энтропия – это мера хаоса…
- 12. Статистическая мера информацииЭнтропия – количественная мера неопределенности
- 13. Статистическая мера информацииКоличество информации в каждом исходе
- 14. Статистическая мера информацииПолученную величину называют энтропией и
- 15. Статистическая мера информацииМаксимальное значение энтропии достигается при
- 16. Статистическая мера информацииВ случае неполного разрешения имеет
- 17. Статистическая мера информацииАбсолютная избыточность информации Dабс представляет
- 18. Семантическая мера информацииСодержательность событияЛогическое количество информацииМера целесообразности информации
- 19. Семантическая мера информацииСодержательность события выражается через функцию
- 20. Семантическая мера информацииМера целесообразности информации определяется как
- 21. Преобразование информацииДискретные сообщения состоят из конечного множества
- 22. Преобразование информацииРазновидности сигналов, которые описываются функцией x(t).1.
- 23. Преобразование информацииРазновидности сигналов, которые описываются функцией x(t).3.
- 24. Преобразование информацииОперацию, переводящую информацию непрерывного вида в
- 25. Преобразование информацииСовместное применение операций дискретизации и квантования
- 26. Преобразование информацииПри дискретизации сигналов приходится решать вопрос
- 27. Преобразование информацииДискретизация называется равномерной (рис. а), если
- 28. Xtt1 t2 t3
- 29. Преобразование информацииКвантование по уровню состоит в преобразовании
- 30. Преобразование информацииКвантование по уровню может быть равномерным
- 31. Xt
- 32. Преобразование информацииТак как в процессе преобразования значение
- 33. Преобразование информацииМетод дискретизации при преобразовании непрерывной информации
- 34. Преобразование информацииДля практических задач, однако, идеально точное
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
- 38. Слайд 38
- 39. Слайд 39
- 40. Слайд 40
- 41. Слайд 41
- 42. Слайд 42
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Слайд 47
- 48. Слайд 48
- 49. Слайд 49
- 50. Слайд 50
- 51. Слайд 51
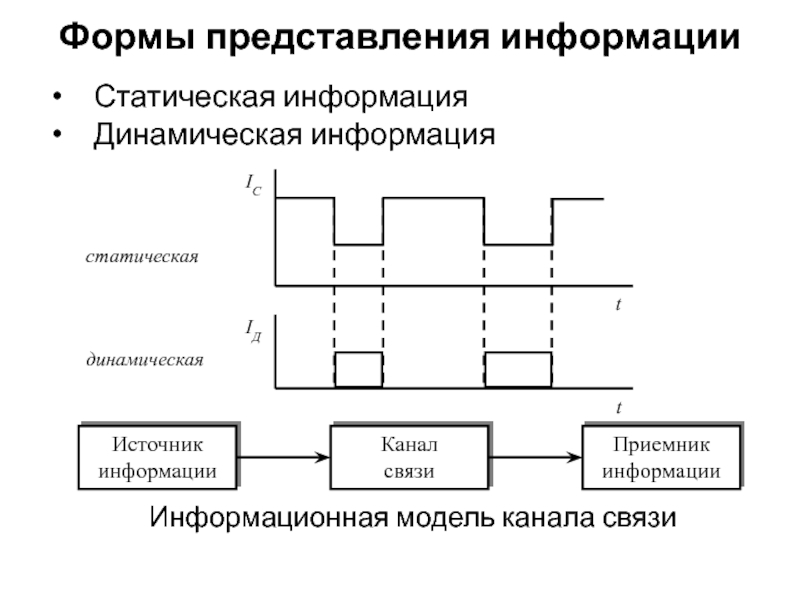
- 52. Формы представления информацииСтатическая информацияДинамическая информацияИнформационная модель канала связи
- 53. Формы представления информацииКодирование – преобразование сообщения в
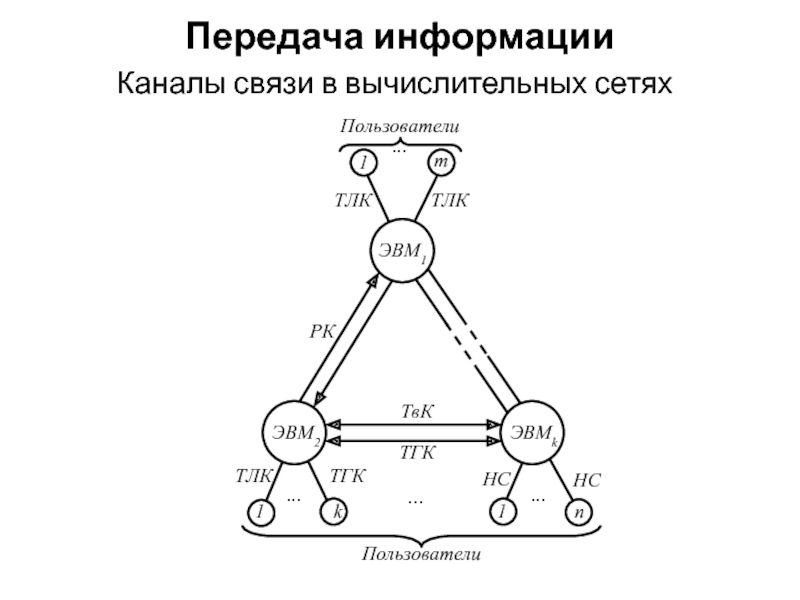
- 54. Передача информацииКаналы связи: непосредственная связь, телефонный канал,
- 55. Передача информацииКаналы связи в вычислительных сетях
- 56. Передача информацииЕсли через канал связи без помех
- 57. Передача информацииКоличество информации в сообщениях максимально при
- 58. Передача информацииДля наиболее эффективного использования канала связи
- 59. Передача информацииПри передаче информации через канал с
- 60. Передача информацииПропускной способностью канала с шумами называется
- 61. Передача информацииПропускная способность канала связи при ограниченной
- 62. Передача информацииСледовательно, можно передавать информацию по каналу
- 63. Фазы преобразования информацииПодготовка информацииРегистрация информацииСбор и передачаОбработкаВывод
- 64. Фазы преобразования информацииНезависимо от фазы преобразования информации
- 65. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Термин "информация" происходит от латинского слова "Informatio" – разъяснение, изложение,
осведомленность.
Слайд 3Свойства информации
Релевантность
Полнота
Своевременность (актуальность)
Достоверность
Доступность
Защищенность
Эргономичность
Адекватность
Слайд 5Тезаурус
Семантические связи между словами или другими смысловыми элементами языка отражают
словарь – тезаурус. Он состоит из двух частей: списка слов
и устойчивых словосочетаний, которые сгруппированы по смыслу, и некоторого ключа, т е. алфавитного словаря, позволяющего расположить слова и словосочетания в определенном порядке. Тезаурус имеет особое значение в системах хранения информации, в которые могут вводиться семантические отношения, в основном подчинения, что позволяет на логическом уровне осуществлять организацию информации в виде отдельных записей, массивов и их комплексов.
Слайд 6Структурная мера информации
Элементарная единицы сообщений – символ
Символы, собранные в группы
– слова
Функция, представленная в непрерывном и дискретном виде
Учитывается только
дискретное строение сообщения, количество содержащихся в нём информационных элементов, связей между ними.Слайд 7Структурная мера информации
Геометрическая мера предполагает измерение параметра геометрической модели информационного
сообщения (длины, площади, объема и т.п.) в дискретных единицах. Например,
геометрической моделью информации может быть линия единичной длины (рисунок а – одноразрядное слово, принимающее значение 0 или 1), квадрат (рисунок б — двухразрядное слово) или куб (рисунок в — трехразрядное слово).
Слайд 8Структурная мера информации
Аддитивная мера (мера Хартли), в соответствии с которой
количество информации измеряется в двоичных единицах — битах (наиболее распространена).
Вводятся понятия глубины q и длины n числа.Глубина q числа – количество символов (элементов), принятых для представления информации. В каждый момент времени реализуется только один какой-либо символ.
Длина n числа – количество позиций, необходимых и достаточных для представления чисел заданной величины.
Слайд 9Структурная мера информации
При заданных глубине и длине числа количество чисел,
которое можно представить, N = qn. Величина N неудобна для
оценки информационной емкости. Введем логарифмическую меру, позволяющую, вычислять количество информации — бит:I(g)=log2 N = n log2 q
Следовательно, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти.
Слайд 10Структурная мера информации
Количество информации при этом эквивалентно количеству двоичных символов
0 или 1. При наличии нескольких источников информации общее количество
информацииI(q1, q2, …, qk) = I(q1) + I(q2)+ … + I(qk),
где I(qk) – количество информации от источника k.
Логарифмическая мера информации позволяет измерять количество информации и используется на практике.
Слайд 11Статистическая мера информации
Энтропия – количественная мера неопределенности и, следовательно, информативности.
Иными
словами, энтропия – это мера хаоса…
Слайд 12Статистическая мера информации
Энтропия – количественная мера неопределенности и, следовательно, информативности.
Пусть
имеется N возможных исходов опыта, из них k разных типов,
а i-й исход повторяется ni раз и вносит информацию, количество которой оценивается как IiТогда средняя информация, доставляемая одним опытом,
Icp = (n1I1 + n2I2 + … + nkIk)/N
Слайд 13Статистическая мера информации
Количество информации в каждом исходе связано с его
вероятностью pi и выражается в двоичных единицах (битах) как Ii=log2
(1/pi)= = –log2 pi. ТогдаIcp = [n1(–log2 p1) + … +nk(–log2 pk)]/N
Выражение можно записать также в виде
Icp = (–log2 p1) + (–log2 p2)+ … + (–log2 p1)
Отношения n/N представляют собой частоты повторения исходов, а следовательно, могут быть заменены их вероятностями ni/N=pi, поэтому их средняя информация в битах
Icp = p1(–log2 p1) + … +pk(–log2 pk)],
или
Icp= – log2 pi = H
Слайд 14Статистическая мера информации
Полученную величину называют энтропией и обозначают обычно буквой
H. Энтропия обладает следующими свойствами:
Энтропия всегда неотрицательна
Энтропия равна нулю в
том крайнем случае, когда одно из pi равно единице, а все остальные — нулюЭнтропия имеет наибольшее значение, когда все вероятности равны между собой: p1 = p2 = ... = pk - 1/k. При этом H = – log2 (1/k) = log2 k
Энтропия объекта AB, состояния которого образуются совместной реализацией состояний A и B, равна сумме энтропии исходных объектов A и B, т. е. H(AB) = H(A) + H(B).
Слайд 15Статистическая мера информации
Максимальное значение энтропии достигается при p=0.5, когда два
состояния равновероятны. При вероятностях p = 0 или p =
1, что соответствует полной невозможности или полной достоверности события, энтропия равна нулю.Количество информации только тогда равно энтропии, когда неопределенность ситуации снимается полностью. В общем случае нужно считать, что количество информации есть уменьшение энтропии вследствие опыта или какого-либо другого акта познания. Если неопределенность снимается полностью, то информация равна энтропии: I = H.
Слайд 16Статистическая мера информации
В случае неполного разрешения имеет место частичная информация,
являющаяся разностью между начальной и конечной энтропией: I = H1–H2.
Наибольшее
количество информации получается тогда, когда полностью снимается неопределенность, причем эта неопределенность была наибольшей – вероятности всех событий были одинаковы. Это соответствует максимально возможному количеству информации I1, оцениваемому мерой Хартли: I1 = log2 N = log2(1/p) = –log2 p ,
где N — число событий; p — вероятность их реализации в условиях равной вероятности событий.
Таким образом, I1 = Hmax
Слайд 17Статистическая мера информации
Абсолютная избыточность информации Dабс представляет собой разность между
максимально возможным количеством информации и энтропией:
Dабс = I1 – H
, или Dабс = Hmax – H .Пользуются также понятием относительной избыточности
D = (Hmax – H)/Hmax
Слайд 18Семантическая мера информации
Содержательность события
Логическое количество информации
Мера целесообразности информации
Слайд 19Семантическая мера информации
Содержательность события выражается через функцию меры m(i) –
содержательности его отрицания. Оценка содержательности основана на математической логике, в
которой логические функции истинности m(i) и ложности m(i ) имеют формальное сходство с функциями вероятностей события p(i) и антисобытия q(i) в теории вероятностей.Как и вероятность, содержательность события изменяется в пределах 0 ≤ m(i) ≤ 1.
Логическое количество информации Inf , сходное со статистическим количеством информации, вычисляется по выражению:
Inf = log2 [1/m(i)] = –log2 m(i )
Слайд 20Семантическая мера информации
Мера целесообразности информации определяется как изменение вероятности достижения
цели при получении дополнительной информации.
Полученная информация может быть пустой,
т. е. не изменять вероятности достижения цели, и в этом случае ее мера равна нулю. В других случаях полученная информация может изменять положение дела в худшую сторону, т.е. уменьшить вероятность достижения цели, и тогда она будет дезинформацией, измеряющейся отрицательным значением количества информации. Наконец, в благоприятном случае получается добротная информация, которая увеличивает вероятность достижения цели и измеряется положительной величиной количества информации.Мера целесообразности в общем виде может быть аналитически выражена в виде соотношения
Iцел = log2 p1 – log2 p0 = log2
где p0 и p1 – начальная (до получения информации) и конечная (после получения информации) вероятности достижения цели.
Слайд 21Преобразование информации
Дискретные сообщения состоят из конечного множества элементов, создаваемых источником
последовательно во времени.
Непрерывные сообщения задаются какой-либо физической величиной, изменяющейся
во времени. Получение конечного множества сообщений за конечный промежуток времени достигается путем дискретизации (по времени) и квантования (по уровню).Слайд 22Преобразование информации
Разновидности сигналов, которые описываются функцией x(t).
1. Непрерывная функция непрерывного
аргумента. Значения, которые могут принимать функция x(t) и аргумент t,
заполняют промежутки (xmin, xmax) и (-T, T) соответственно.2. Непрерывная функция дискретного аргумента. Значения функции x(t) определяются лишь на дискретном множестве значений аргумента ti, i=0±1±2, … Величина x(ti) может принимать любое значение в интервале (xmin, xmax).
Слайд 23Преобразование информации
Разновидности сигналов, которые описываются функцией x(t).
3. Дискретная функция непрерывного
аргумента. Значения, которые может принимать функция x(t), образуют дискретный ряд
чисел х1, х2,..., xk. Значение аргумента t может быть любым в интервале (-T, T).4. Дискретная функция дискретного аргумента. Значения, которые могут принимать функция х(t) и аргумент t, образуют дискретные ряды чисел x1, x2, ..., xk и t1, t2, ..., tk, заполняющие интервалы (xmin, xmax) и (-T,T) соответственно.
Слайд 24Преобразование информации
Операцию, переводящую информацию непрерывного вида в информацию дискретного вида,
называют квантованием по времени, или дискретизацией. Следовательно, дискретизация состоит в
преобразовании сигнала x(t) непрерывного аргумента t в сигнал x(ti) дискретного аргумента ti.Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала x(ti) в дискретное множество значений xk, k = =0,1,..., (m - 1); xk ∈ (xmin, xmax) (третий вид сигнала).
Слайд 25Преобразование информации
Совместное применение операций дискретизации и квантования по уровню позволяет
преобразовать непрерывный сигнал x(t) в дискретный по координатам x и
t(четвертая разновидность).В результате дискретизации исходная функция x(t) заменяется совокупностью отдельных значений x(ti). По значениям функции x(ti) можно восстановить исходную функцию x(t) с некоторой погрешностью. Функцию, полученную в результате восстановления (интерполяции) по значениям x(ti), будем называть воспроизводящей и обозначать V(t).
Слайд 26Преобразование информации
При дискретизации сигналов приходится решать вопрос о том, как
часто следует проводить отсчеты функции, т. е. каков должен быть
шаг дискретизации Δti = ti – ti-1. При малых шагах дискретизации количество отсчетов функции на отрезке обработки будет большим и точность воспроизведения — высокой. При больших шагах дискретизации количество отсчетов уменьшается, но при этом, как правило, снижается точность восстановления. Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве отсчетов.Слайд 27Преобразование информации
Дискретизация называется равномерной (рис. а), если длительность интервалов Δti
= const на всем отрезке обработки сигнала.
Дискретизация называется неравномерной (рис.
б), если длительность интервалов между отсчетами Δti , различна, т. е. Δti = var.
Слайд 29Преобразование информации
Квантование по уровню состоит в преобразовании непрерывных значений сигнала
x(ti) в моменты отсчета ti, в дискретные значения.
В соответствии
с графиком изменения функции x(t) ее истинные значения представляются в виде заранее заданных дискретных уровней 1, 2, 3, 4, 5 или 6.
Слайд 30Преобразование информации
Квантование по уровню может быть равномерным и неравномерным в
зависимости от величины шага квантования. Под шагом (интервалом) квантования δm
понимается разность δm = xm – xm-1, где xm, xm-1 – соседние уровни квантования.Уровень квантования для заданного значения сигнала x(t) можно выразить двумя способами:
сигнал x(ti) отождествляется с ближайшим уровнем квантования;
сигнал x(ti) отождествляется с ближайшим меньшим (или большим) уровнем квантования.
Слайд 32Преобразование информации
Так как в процессе преобразования значение сигнала x(t) отображается
уровнем квантования xm , а каждому уровню m может быть
поставлен в соответствие свой номер (число), то при передаче или хранении информации можно вместо истинного значения величины xm использовать соответствующее число m.Такое преобразование сопровождается шумами или погрешностью квантования. Погрешность квантования связана с заменой истинного значения сигнала x(ti) значением, соответствующим уровню квантования xm.
Слайд 33Преобразование информации
Метод дискретизации при преобразовании непрерывной информации в дискретную влияет
на количество информации, которую надо хранить или преобразовывать в ЭВМ.
Важна теорема Котельникова, согласно которой функция, имеющая ограниченный спектр частот, полностью определяется дискретным множеством своих значений, взятых с частотой отсчетов: F0 = 2fm , где fm = 2πωm – максимальная частота в спектре частот S(jω) сигнала x(t); ωm –угловая скорость.Функция x(t) воспроизводится без погрешностей по точным значениям x(ti) в виде ряда Котельникова:
где Δt – шаг дискредитации.
Слайд 34Преобразование информации
Для практических задач, однако, идеально точное восстановление функций не
требуется, необходимо лишь восстановление с заданной точностью. Поэтому теорему Котельникова
можно рассматривать как приближенную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют по формулеF0 = 2fmaxk3 ,
где k3 — коэффициент запаса (обычно 1,5
Слайд 52Формы представления информации
Статическая информация
Динамическая информация
Информационная модель канала связи
Слайд 53Формы представления информации
Кодирование – преобразование сообщения в форму, удобную для
передачи по данному каналу
Декодирование – операция восстановления принятого сообщения
Информационная модель
канала связи с шумамиШум
Слайд 54Передача информации
Каналы связи: непосредственная связь, телефонный канал, телеграфный канал, радиоканал,
телевизионный канал и т.д.
Пропускная способность – характеристика канала связи, которая
не зависит от скорости передачи информации.Пропускная способность канала с шумами – максимальная скорость передачи информации при условии, что канал связи без помех согласован с источником информации.
Слайд 56Передача информации
Если через канал связи без помех передается последовательность дискретных
сообщений длительностью T, то скорость передачи информации по каналу связи
(бит/с)где I – количество информации, содержащейся в последовательности сообщений.
Предельное значение скорости передачи информации называется пропускной способностью канала связи без помех c = vmax.
Передача информации по каналу без помех
Слайд 57Передача информации
Количество информации в сообщениях максимально при равной вероятности состояний.
Тогда
Скорость передачи информации в общем случае зависит от статистических свойств
сообщений и параметров канала связи.Передача информации по каналу без помех
Слайд 58Передача информации
Для наиболее эффективного использования канала связи необходимо, чтобы скорость
передачи информации была как можно ближе к пропускной способности канала
связи. Если скорость поступления информации на вход канала связи превышает пропускную способность канала, то по каналу будет передана не вся информация. Основное условие согласования источника информации и канала связи v ≤ c.Согласование осуществляется путем соответствующего кодирования сообщений.
Передача информации по каналу без помех
Слайд 59Передача информации
При передаче информации через канал с помехами сообщения искажаются,
и на приемной стороне нет уверенности в том, что принято
именно то сообщение, которое передавалось. Следовательно, сообщение недостоверно, вероятность правильности его после приема не равна единице. В этом случае количество получаемой информации уменьшается на величину неопределенности, вносимой помехами, т. е. вычисляется как разность энтропии сообщения до и после приема: I’ = H(i) – Hi(i), где H(i) – энтропия источника сообщений; Hi(i) – энтропия сообщений на приемной стороне.Таким образом, скорость передачи по каналу связи с помехами:
Передача информации по каналу с помехами
Слайд 60Передача информации
Пропускной способностью канала с шумами называется максимальная скорость передачи
информации при условии, что канал связи без помех согласован с
источником информации:Если энтропия источника информации не превышает пропускной способности канала (H ≤ c), то существует код, обеспечивающий передачу информации через канал с помехами со сколь угодно малой частотой ошибок или сколь угодно малой недостоверностью.
Передача информации по каналу с помехами
Слайд 61Передача информации
Пропускная способность канала связи при ограниченной средней мощности аналогового
сигнала:
где Fm – полоса частот канала (Гц); Wс – средняя
мощность сигнала; Wm — средняя мощность помех (равномерный спектр) с нормальным законом распределения амплитуд в полосе частот канала связи.Передача информации по каналу с помехами
Слайд 62Передача информации
Следовательно, можно передавать информацию по каналу с помехами без
ошибок, если скорость передачи информации меньше пропускной способности канала. Для
скорости v > c при любой системе кодирования частота ошибок принимает конечное значение, причем оно растет с увеличением значения v. Для канала с весьма высоким уровнем шумов (Wm >> Wc) максимальная скорость передачи близка к нулю.Передача информации по каналу с помехами
Слайд 63Фазы преобразования информации
Подготовка информации
Регистрация информации
Сбор и передача
Обработка
Вывод и воспроизведение
Наряду с
крупными этапами или фазами преобразования информации существуют более мелкие операции,
связанные с отдельными воздействиями на информацию для получения каких-то данных по заранее известным алгоритмам: классификация, синтез.Слайд 64Фазы преобразования информации
Независимо от фазы преобразования информации каждый вид ее
обладает определенными характеристиками, среди которых полезно выделить связанные с функционированием
ИС следующие характеристики:Цель информации
Формат
Избыточность
Периодичность появления
Верность