Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы математического анализа
Содержание
- 1. Основы математического анализа
- 2. Лекция 1Числовые последовательностиФункции одной переменнойПределы последовательностей и функцийНепрерывность
- 3. Числовая последовательность
- 4. Числовая последовательностьПоследовательностью элементов числового множества Х называется
- 5. Стационарная последовательность xn = а для всех
- 6. Последовательность может задаваться: 1) формулой ее общего члена,
- 7. Последовательность {xn} называется ограниченной сверху (снизу), если
- 8. Последовательность {xn} называется бесконечно большой (бесконечно малой),
- 9. Последовательность действительных чисел {xn} называется сходящейся к
- 10. При этом говорят также, что число А является пределом данной последовательности и пишут
- 11. Если последовательность не является сходящейся, ее называют расходящейся
- 12. Если последовательность {xn} бесконечно большая (а следовательно,
- 13. Слайд 13
- 14. Скачать презентанцию
Лекция 1Числовые последовательностиФункции одной переменнойПределы последовательностей и функцийНепрерывность
Слайды и текст этой презентации
Слайд 2Лекция 1
Числовые последовательности
Функции одной переменной
Пределы последовательностей и функций
Непрерывность
Слайд 4Числовая последовательность
Последовательностью элементов числового множества Х называется функция f, определенная
Слайд 5Стационарная последовательность
xn = а для всех n=1,2, .
Конечная
последовательность отображение начального отрезка натурального ряда {1, 2, ,
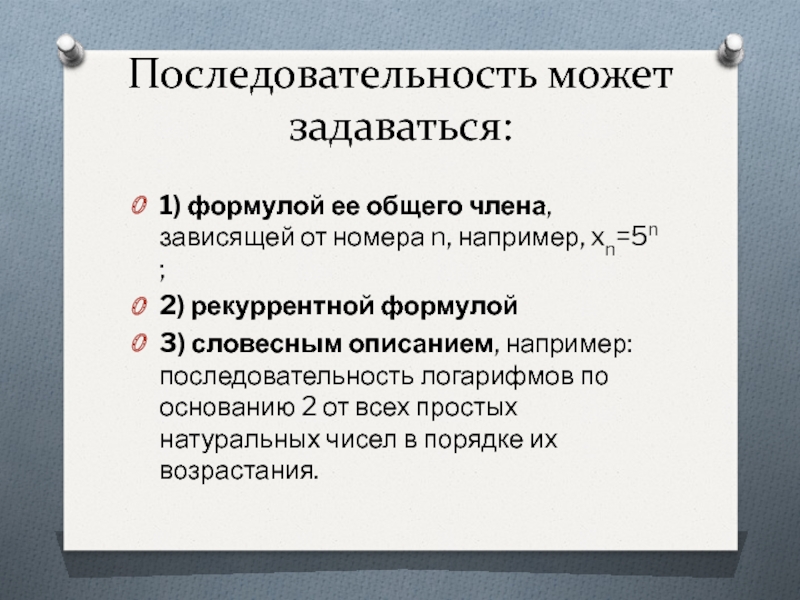
n} в множество Х.Слайд 6Последовательность может задаваться:
1) формулой ее общего члена, зависящей от номера n,
например, xn=5n ;
2) рекуррентной формулой
3) словесным описанием, например: последовательность логарифмов по основанию
2 от всех простых натуральных чисел в порядке их возрастания. Слайд 7Последовательность {xn} называется ограниченной сверху (снизу), если существует число S
(s), большее (меньшее) любого ее члена, т.е.
n хn
S (n xn s). Если последовательность {xn} ограничена и сверху, и снизу, то она называется ограниченной.
Слайд 8Последовательность {xn} называется бесконечно большой (бесконечно малой), если для любого
положительного числа существует номер N такой, что при всех
n N выполняется условие |xn| (|xn| ).Формальная запись:
N n n>N |xn| (|xn| ).
Слайд 9Последовательность действительных чисел {xn} называется сходящейся к числу А, если
для любого 0 существует такое натуральное число N,
что для всех n N выполняется условие .Формальная запись:
N n n>N |xn - A| .
Слайд 12Если последовательность {xn} бесконечно большая (а следовательно, расходящаяся), то условно
пишут
если при этом, начиная с некоторого номера N, все
элементы положительны (отрицательны), то условно пишут Для бесконечно малой последовательности, очевидно,