Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории алгоритмов
Содержание
- 1. Основы теории алгоритмов
- 2. 6.1 Интуитивное понятие об алгоритмеИнтуитивное понятие алгоритма.Алгоритм
- 3. Правила описания алгоритмов:Понятность для исполнителяМассовость (т.е. допустимость
- 4. Алгоритм применим к допустимому исходному
- 5. Поскольку требование завершения алгоритмического процесса за конечное
- 6. Об источниках алгоритмов:Практика;научная теория;совокупность накопленных алгоритмов;изобретательность разработчика.
- 7. 6.2 Три типа алгоритмических моделей Различный
- 8. Первый тип Связывает понятие алгоритма с
- 9. Второй тип Основан на представлении об
- 10. Третий тип Это преобразование слов в
- 11. Тезис Чёрга Класс задач, решаемых в любой
- 12. Примеры.Задача о квадратуре круга.Требуется найти алгоритм построения
- 13. Примеры.Задача удвоения куба.Найти алгоритм, позволяющий на стороне
- 14. Вторая причина разработки теории алгоритмов – необходимость
- 15. Пример Актуально бесконечное множество. Расходуя ограниченное
- 16. 6.3 Кризис теории множеств антиномии. Выводы из
- 17. На втором Международном Математическом Конгрессе
- 18. Две теории Кантора из теории множеств Кардинальное
- 19. Парадокс Кантора. Пусть М множество
- 20. Парадокс Рассела (парадокс брадобрея). Один
- 21. Открытие антиномий потрясло математику и
- 22. 6.4 Машины Тьюринга как модели алгоритмов
- 23. Машина состоит из бесконечной в
- 24. Основной частью машины является логический
- 25. Т.о. работа МТ задается системой команд вида:
- 26. Если головка в состоянии qj
- 27. Слайд 27
- 28. Примеры построения машин ТьюрингаПостороить машину Тьюринга, реализущую.
- 29. Слайд 29
- 30. Построить машину Тьюринга, которая вычисляет функцию а(Х)=Х+1
- 31. В первом случае говорят, что машина применила
- 32. Тезис Тьюринга: Любая вычислимая функция вычислимая
- 33. Проблема остановки: Можно ли построить машину
- 34. Теорема Тьюринга: Не существует машины То
- 35. Скачать презентанцию
6.1 Интуитивное понятие об алгоритмеИнтуитивное понятие алгоритма.Алгоритм – это правило, сформированное на некотором языке и определяющее процесс переработки допустимых исходных данных в искомые результаты. Допустимыми исходными данными для этого правила являются
Слайды и текст этой презентации
Слайд 3Правила описания алгоритмов:
Понятность для исполнителя
Массовость (т.е. допустимость для него всех
предложений языка исходных данных)
Определенность (все шаги алгоритма детерминированы и четко
определены)Результативность
Слайд 4 Алгоритм применим к допустимому исходному данному, если с
его помощью, отправляясь от этого исходного данного, можно получить искомый
результат. При этом алгоритмический процесс оканчивается после конечного числа шагов и на каждом шаге нет препятствий для его выполнения.
Слайд 5Поскольку требование завершения алгоритмического процесса за конечное число шагов не
учитывает реальных возможностей, связанных с затратами времени и ресурсов, то
говорят, что при этом алгоритм потенциально выполним.
Слайд 6Об источниках алгоритмов:
Практика;
научная теория;
совокупность накопленных алгоритмов;
изобретательность разработчика.
Слайд 76.2 Три типа алгоритмических моделей
Различный выбор исходных средств
формализации приводит к моделям алгоритмов разного вида. Можно выделить три
основных типа универсальных алгоритмических моделей, различающихся исходными эвристическими соображениями относительно того, что такое алгоритм.
Слайд 8Первый тип
Связывает понятие алгоритма с вычислениями и числовыми
функциями. Наиболее развитая и изученная модель этого типа – рекурсивные
функции – первый способ формализации понятия алгоритма.
Слайд 9Второй тип
Основан на представлении об алгоритме как о
некотором детерминированном устройстве, способном выполнять в каждый отдельный момент лишь
примитивные операции (машина Тьюринга).
Слайд 10Третий тип
Это преобразование слов в произвольных алфавитах, в
которых элементарными операциями являются подстановки, т.е. замена куска слова (подслова)
другим словом (Нормальный алгоритм Маркова, каноническая система Поста).
Слайд 11Тезис Чёрга
Класс задач, решаемых в любой из этих формальных
моделей, и есть класс всех задач, которые могут быть решены
интуитивно алгоритмическими методами.Одна из причин, побудивших заняться теорией алгоритмов, – это подозрительность математиков в связи с накоплением упорно не поддающихся решению задач на нахождение алгоритмов.
Слайд 12Примеры.
Задача о квадратуре круга.
Требуется найти алгоритм построения с помощью циркуля
и линейки квадрата, равновеликого данному кругу.
Задача трисекции угла.
Требуется найти алгоритм
деления произвольного угла с помощью циркуля и линейки на три равные части 
Слайд 13Примеры.
Задача удвоения куба.
Найти алгоритм, позволяющий на стороне любого куба с
помощью циркуля и линейки построить сторону куба, объем которого вдвое
больше объема заданного куба.
Слайд 14Вторая причина разработки теории алгоритмов – необходимость обоснования математики, поскольку
появления антиномий привели к тому, что все в математике стало
казаться неустойчивым.
Слайд 15Пример
Актуально бесконечное множество. Расходуя ограниченное количество ресурсов на
каждом шаге, имеющим фиксированную длительность, построить такое множество ни реально,
ни потенциально нельзя; нельзя проверить обладает ли все элементы такого множества каким либо свойством из-за ограниченной скорости проверки.
Слайд 166.3 Кризис теории множеств антиномии. Выводы из антиномий.
До
середины XIX века никто не сомневался в истинности математических результатов,
залогом чего считалась истинность аксиом. Исследования Лобачевского сокрушили веру в аксиомы и заставили задуматься над тем, что же является фундаментом математики. Оказалось, что все вопросы можно свести к рассмотрению только натуральных чисел и некоторых отношений между ними. Была доказана возможность полной арифметизации матанализа и теории функций.
Слайд 17 На втором Международном Математическом Конгрессе было заявлено, что
теперь в математике остались только целые числа и конечные или
бесконечные множества целых чисел. Математика полностью арифметизирована. И вот тогда, когда математика обрела надежный фундамент сама арифметика пошатнулась из-за того что в теории множеств были обнаружены противоречия, вошедшие в историю математики под названием антиномий.
Слайд 18Две теории Кантора из теории множеств
Кардинальное число множества
М называется его мощностью и обозначается m.
Теорема 1: Для
любого кардинально числа m справедливо неравенство m<2m, где 2m – мощность множества всех подмножеств бесконечного множества.Теорема 2: Мощность m’ подмножества множеств, имеющих мощность m удовлетворяет неравенству m’<= m
Слайд 19 Парадокс Кантора.
Пусть М множество всех множеств обозначим
его кардинальное число буквой m. В силу теоремы 1 кардинальное
число множества его подмножества 2m удовлетворяет условию 2m> m с другой стороны множество m есть множество всех множеств его подмножества являются множествами и значит являются элементом М, а их множества являются подмножествами множества М. По теореме 2 должно иметь место неравенство 2m<= m полученные два неравенства противоречат друг другу
Слайд 20Парадокс Рассела
(парадокс брадобрея).
Один из солдат оказался
по профессии парикмахером, узнав об этом командир приказал ему брить
всех тех и только тех кто сам себя не бреет. Все было хорошо пока не пришло время побрить самого себя оказалось, что побрить самого себя нельзя, так парикмахер брил только тех кто себя не бреет. Не брить себя тоже нельзя, потому что приказано брить всех, кто себя не бреет.
Слайд 21 Открытие антиномий потрясло математику и математиков, как землетрясение.
Нужно сказать, что математики поразному отреагировали на это заявление: одни
стали во всем сомневаться, другие на антиномии не отреагировали.
Слайд 226.4 Машины Тьюринга как модели алгоритмов
В
1937г. английский математик Тьюринг опубликовал работу в которой он уточняя
понятие алгоритма, прибегал к воображаемой вычислительной машине.Машина должна перерабатывать какие-то объекты в исходные результаты. Этими объектами являются слова, построенные из символов-букв.
Слайд 23 Машина состоит из бесконечной в обе стороны ленты,
разбитой на ячейки, и рабочей головки. Машина работает в дискретные
моменты времени t=0,1,2… В каждый момент времени во всякой ячейке ленты записана одна буква из некоторого конечного алфавита А={а0, а1, а2…аn}, называемым внешним алгоритмом машины, а головка находится в одном состояний из конечного множества внутренних состояний Q={q0, q1…qz}. Будем считать,что а0-пустой символ, т.е. в ячейке ничего не написано.
Слайд 24 Основной частью машины является логический блок, который работает
следующим образом. В каждый момент времени рабочая головка обозревает одну
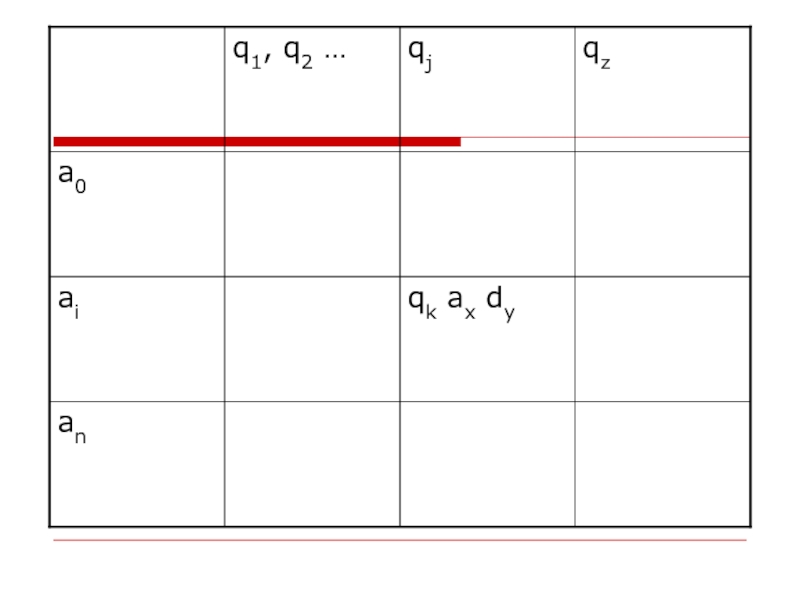
ячейку ленты и в зависимости от того, что там написано и от своего внутреннего состояния она заменяет символ в обозреваемой ячейке, переходит в новой состояние и сдвигает на одну ячейку или остается на месте. Введем для обозначения этого движения символы d-1, d0, d+1 соответственно.
Слайд 25Т.о. работа МТ задается системой команд вида:
qj*ai-qk*ax*dy
Все случаи сочетания
qj и ai для разных j и j и все
реакции машины на них можно представить в виде функциональной таблицы с двумя входами.
Слайд 26 Если головка в состоянии qj читаем символ ai,
то в следующий момент она записывает в эту ячейку символ
ax. Переход в состояние qk и в зависимости от того каково dy гловка сдвигает на одну ячейку влево, вправо или остается на месте.
Слайд 28Примеры построения машин Тьюринга
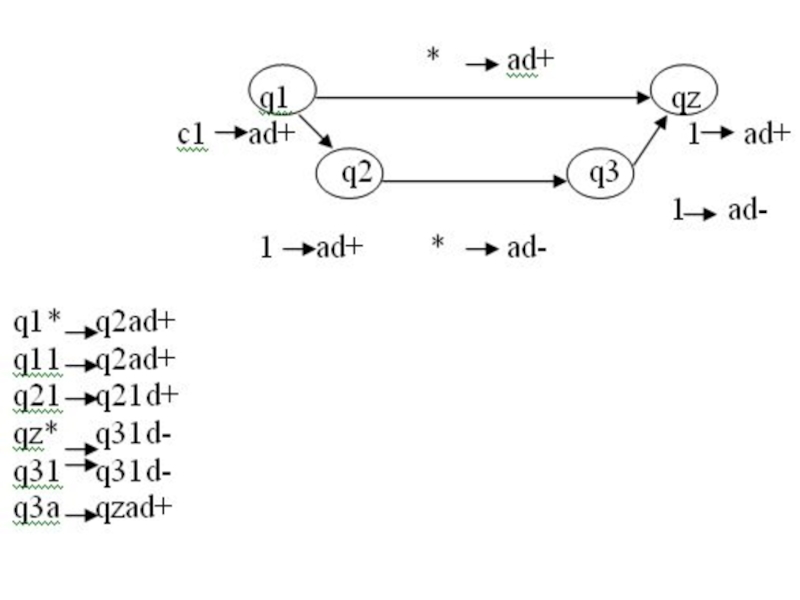
Постороить машину Тьюринга, реализущую. «сложение» чисел.
В машине
Тюринга все числа представляются в единичном коде, состоящем из Х
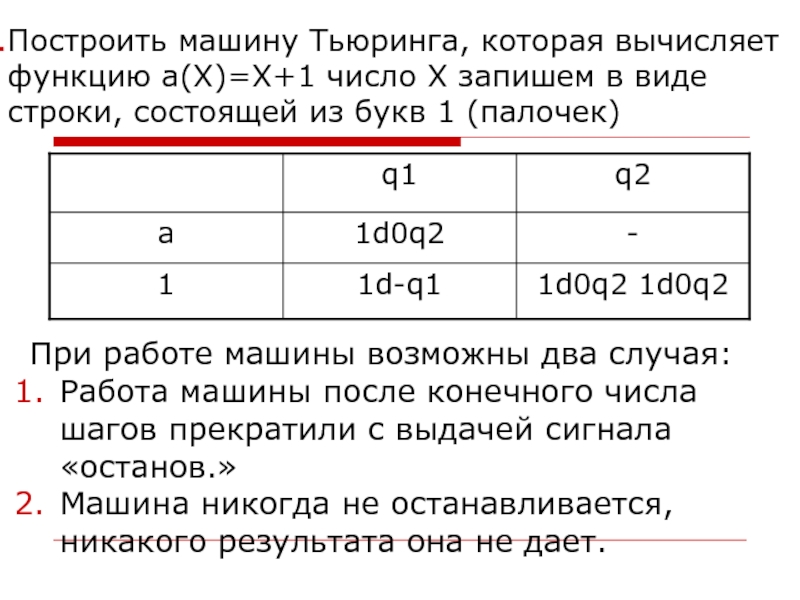
единиц. Поэтому сложить а и в значит переработать слова 1а * 1в в слово 1а+в. Это преобразование выполняет машина c 4-мя состояниями и системой команд вида
Слайд 30Построить машину Тьюринга, которая вычисляет функцию а(Х)=Х+1 число Х запишем
в виде строки, состоящей из букв 1 (палочек)
При работе машины
возможны два случая:Работа машины после конечного числа шагов прекратили с выдачей сигнала «останов.»
Машина никогда не останавливается, никакого результата она не дает.
Слайд 31В первом случае говорят, что машина применила к исходному данному,
во втором – не применима. Соответствия устанавливаются между теми исходными
данными, к которым они применимы, и результат ее работы представляет собой некоторую функцию (в математическом смысле).Если для функции f(x) можно построить МТ, которая к ней применима, то говорят, что f(x) вычислена по Тьюрингу. Функцию, для вычисления которой существует МТ, называют вычислимой.
Слайд 32Тезис Тьюринга:
Любая вычислимая функция вычислимая по Тьюрингу,
или всякий алгоритм может быть реализован машиной Тьюринга.
Слайд 33Проблема остановки:
Можно ли построить машину То такую что
для любой машины Тк любых исходных данных а для машины
Т.Ответ на этот вопрос отрица-тельный, т.к. сформулирована и доказана следующая теорема.
Слайд 34Теорема Тьюринга:
Не существует машины То , решающей
проблему остановки для произвольной машины Т.
Неразрешимость проблемы оста-новки
можно интерпретировать как несуществование общего алгоритма для отладки программы. 
