ОТС 6 Показатели вариации.ppt

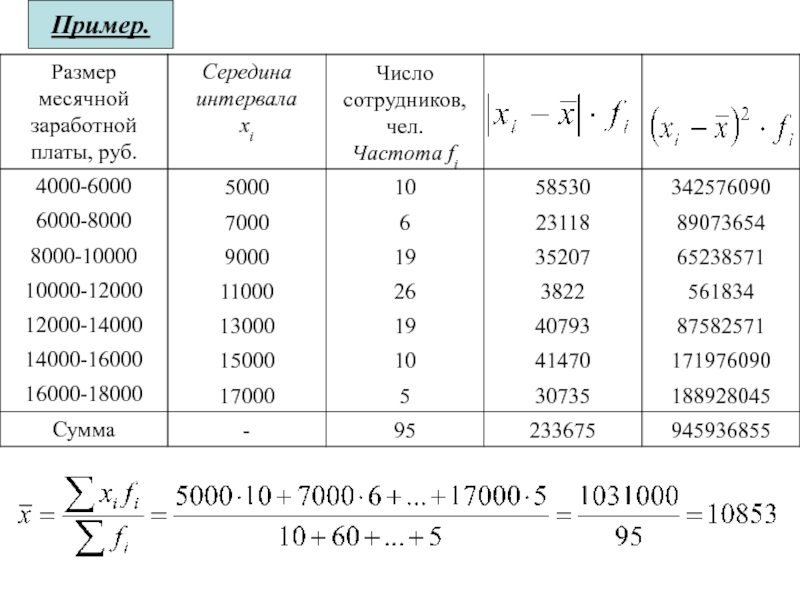
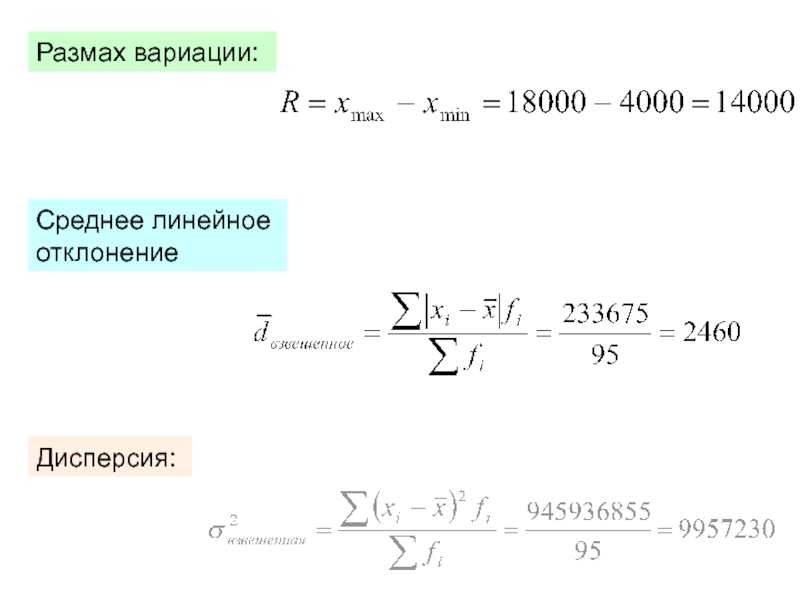
у единиц статистической совокупности.
К абсолютным показателям вариации относятся размах

вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение (стандартное отклонение).

Размах вариации (R) вычисляется как разность между максимальным и минимальным значениями признака:

значений отклонений отдельных значений признака от их среднего.
Если ряд

не сгруппирован, то для расчетов используется простая невзвешенная формула среднего линейного отклонения:

Для вариационного ряда с неравными частотами следует использовать взвешенную формулу

от их среднего:




для несгруппированных данных:

для вариационных рядов
с неравными частотами:

Квадратный корень из дисперсии называется средним квадратическим отклонением

к разным совокупностям, используют относительные показатели вариации.
коэффициент осцилляции:

относительное

линейное отклонение:

коэффициент вариации:

С помощью коэффициента вариации также можно охарактеризовать степень однородности совокупности.

количество групп, то становится возможным оценить степень зависимости вариации значений

показателя, характеризующего единицы наблюдения, от признака, положенного в основу группировки.


Так, если значения кредитной ставки банков сгруппированы в зависимости от срока кредита, то рассчитав эмпирический коэффициент детерминации, мы получим ответ на вопрос, насколько величина кредитной ставки банка определяется тем, на какой срок предоставляется кредит.

Вычисляется общая дисперсия:
Общая дисперсия характеризует вариацию значений признака за счет

всех факторов: как положенного в основу группировки, так и остальных неучтенных, но действующих на исследуемый признак.

3. По каждой группе рассчитываются групповые средние:

внутри групп независимо от того, какое значение принимает группировочный признак

(оценивается влияние на показатель факторов отличных от группировочного).

.
6. Определяется межгрупповая дисперсия:
Межгрупповая дисперсия характеризует вариацию значений исследуемого

признака за счет действия на него только группировочного признака.

определенная зависимость, известная под термином «правило сложения дисперсий», а именно:

.

данный коэффициент показывает, какая процентная доля общей вариации значений признака

объясняется действием фактора, положенного в основу группировки (группировочным признаком).

Т.е. величина кредитной ставки на 21 % зависит от срока предоставления банком кредита.

эмпирическое корреляционное отношение, которое представляет собой квадратный корень из коэффициента

детерминации:

.

Эмпирическое корреляционное отношение изменяется в переделах от 0 до 1. Нулевое значение говорит о том, что связи нет (тогда межгрупповая дисперсия равна 0). Значение 1 указывает на наличие функциональной зависимости между признаками, при которой значения исследуемого показателя полностью определяются значениями группировочного признака (средняя из внутригрупповых дисперсий в этом случае принимает нулевое значение).

к 1, тем связь теснее.

Чем ближе значение