ефектами (червоність).
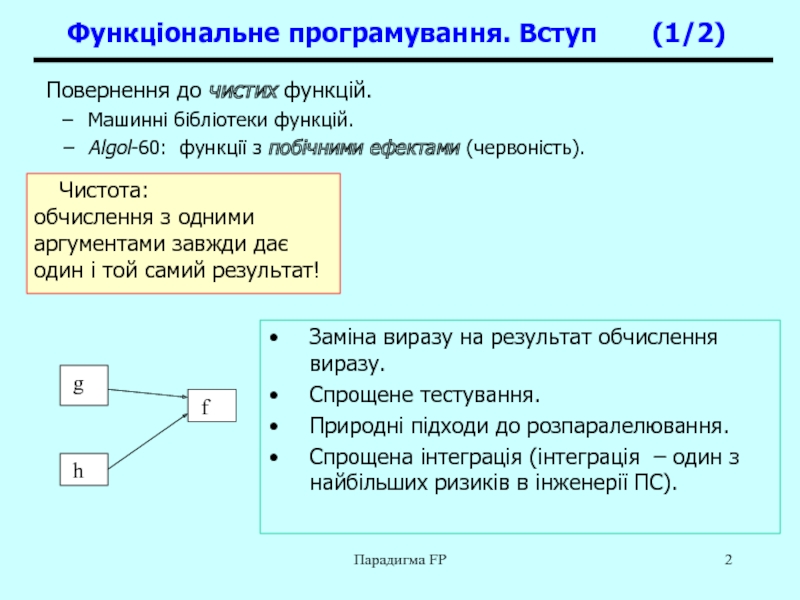
Функціональне програмування. Вступ (1/2)
Чистота:
обчислення з одними
аргументами завжди дає один і той самий результат! g
f
h
Заміна виразу на результат обчислення виразу.
Спрощене тестування.
Природні підходи до розпаралелювання.
Спрощена інтеграція (інтеграція – один з найбільших ризиків в інженерії ПС).




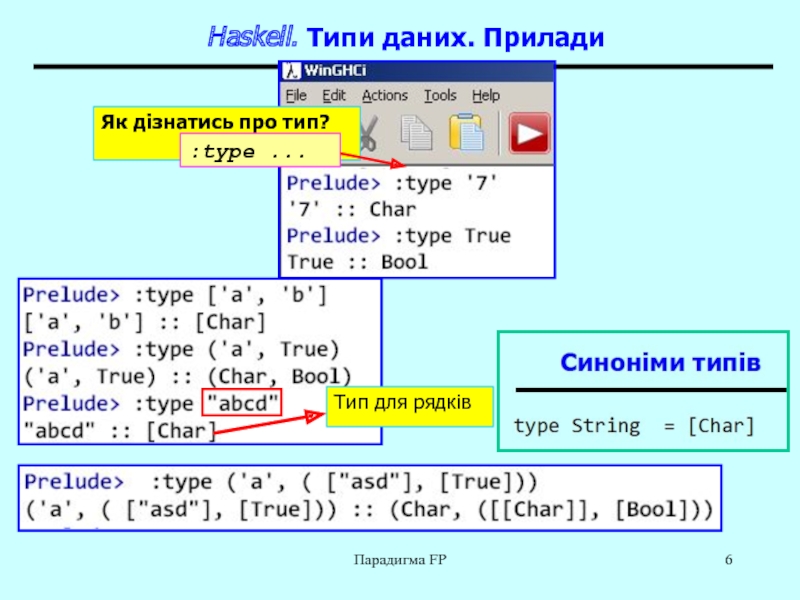
![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPСиноніми типівtype String = [Char]type PairInt = (Int,Int) type Pair Парадигма FPСиноніми типівtype String = [Char]type PairInt = (Int,Int) type Pair = (a,b)type Vector = (Double, Double)type](/img/thumbs/78830debf15e404a1eae51ee147f6018-800x.jpg)
![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPТип [a] є прикладом поліморфного тип. З ним пов’язується сімейство Парадигма FPТип [a] є прикладом поліморфного тип. З ним пов’язується сімейство будь-яких типів списків з (однотипними!) елементами](/img/thumbs/495ca87ac54d0d3d96a8a8fb6dfb839c-800x.jpg)


![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FP Приклад 2. (Два рівняння).Параметричний поліморфізм (2/3)head1 (x:_) = Парадигма FP Приклад 2. (Два рівняння).Параметричний поліморфізм (2/3)head1 (x:_) = xhead1 [] =](/img/thumbs/7626869623c4358a92772a1bf2a729d7-800x.jpg)


![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPПриклад 1.Приклад 2.До визначення функцій. Рекурсивні функціїlast :: [a] -> Парадигма FPПриклад 1.Приклад 2.До визначення функцій. Рекурсивні функціїlast :: [a] -> a last [x] = x last](/img/thumbs/971fb394c9d06bd2f6b8ec3121116587-800x.jpg)
![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPДо визначення функцій. Каррінг (1/2)[a] -> [a] -> [a][a] -> Парадигма FPДо визначення функцій. Каррінг (1/2)[a] -> [a] -> [a][a] -> ([a] -> [a])?Реальний тип reverse1. Тобто](/img/thumbs/ef1ab20eae7ac61fe986be678fd35eea-800x.jpg)
![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPДо визначення функцій. Каррінг (2/2)reverse1 [] y = yreverse1 Парадигма FPДо визначення функцій. Каррінг (2/2)reverse1 [] y = yreverse1 (x:xs) y = reverse1 xs](/img/tmb/3/209399/4f8b068f6c705cf79da23050ce2f4695-800x.jpg)


![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPФункції як аргументи. Кілька прикладівmap1 :: (a->b) -> Парадигма FPФункції як аргументи. Кілька прикладівmap1 :: (a->b) -> [a] -> [b]map1](/img/tmb/3/209399/c3176291d9d4b292d9b91368b62d7b27-800x.jpg)

![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPHaskell-програми. Приклади (2/3)getDivisors num | num < 1 Парадигма FPHaskell-програми. Приклади (2/3)getDivisors num | num < 1 = [] |](/img/thumbs/94e078d249993b03ed069468ebfcab4e-800x.jpg)
![Парадигма функціонального програмування. Знайомство з мовою Haskell Парадигма FPHaskell-програми. Приклади (3/3)zipF :: (a -> b -> c) -> Парадигма FPHaskell-програми. Приклади (3/3)zipF :: (a -> b -> c) -> [a] -> [b] -> [c]zipF](/img/tmb/3/209399/f48a7c5fe7130c7355db4ed30d768a5b-800x.jpg)