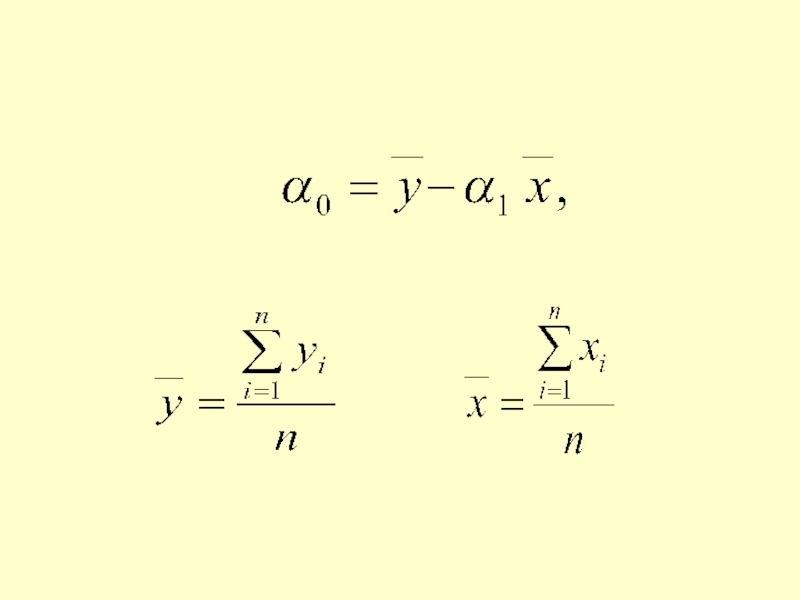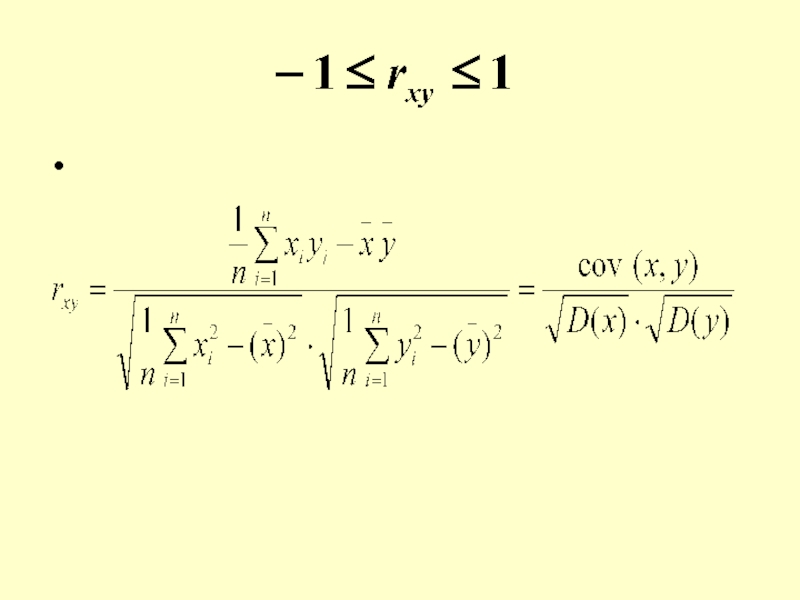Слайд 2Тема 2. Парна лінійна регресія
Загальний вигляд лінійної економетричної моделі. Специфікація
моделі.
Передумови застосування методу найменших квадратів (МНК). Оцінка параметрів лінійної регресії
за допомогою МНК.
Коефіцієнти кореляції та детермінації.
Властивості оцінок, їх характеристика. Поняття про ступені вільності.
Перевірка моделі на адекватність за допомогою F–критерію Фішера.
Критерій Стьюдента перевірки значимості параметрів моделі та коефіцієнта кореляції генеральної сукупності.
Побудова інтервалів довіри параметрів моделі.
Економічна інтерпретація параметрів моделі.
Прогнозування за моделями парної лінійної регресії.
Слайд 31. Загальне поняття про лінійну регресію. Специфікація
аналіз зв’язку між
змінними - використовується термін «регресія»
вимір тісноти зв’язку між змінними
- термін «кореляція»
Слайд 4Функція, що відображає статистичний зв'язок між змінними, називається рівнянням регресії
Якщо таке рівняння зв'язує лише дві змінні, це рівняння парної
(простої) регресії
Якщо воно відображає залежність результативної змінної від двох або більше незалежних змінних - це рівняння множинної регресії.
Слайд 5Специфікація моделі
це аналітична форма економетричної моделі. Вона складається з певного
виду функції чи функцій, що використовуються для побудови моделей, має
ймовірнісні характеристики, які притаманні стохастичним залишкам моделі.
Слайд 7Прості лінійні регресійні моделі встановлюють лінійну залежність між двома змінними
(парна регресія)
Наприклад
між ціною на товар та попитом на нього
витратами на рекламу та обсягом продукції, що випускається
витратами на споживання та валовим національним продуктом (ВНП).
Слайд 8
Лінійна регресія є найпоширенішим і простим видом залежності між
економічними змінними і часто служить початковою (відправною) точкою економічного аналізу
При цьому одна із змінних вважається залежною змінною (результативною ознакою у) та розглядається як функція від незалежної змінної (факторної ознаки х).
Слайд 9проста регресійна модель має вигляд
де
— вектор спостережень за залежною
змінною
х — вектор спостережень за незалежною
змінною
— теоретичні параметри регресійної моделі
Слайд 10е — вектор помилок
є випадковою величиною, що характеризує відхилення у від теоретичної регресії і вказує на стохастичну суть регресійної залежності
Помилки ще називають відхиленнями або залишками
Слайд 11
В рівнянні (1) складова
називається системною складовою
регресії (вона обумовлена лінійною залежністю між змінними)
е називається випадковою складовою регресії (обумовлена впливом випадкових факторів)
Слайд 12Таким чином
рівняння (1) є лінійною регресійною моделлю, яку
ще можна трактувати і як пряму на площині, де
— перетин з віссю ординат, — нахил до осі абсцис, (якщо не враховувати випадкову величину е ).
Слайд 132. Передумови застосування методу найменших квадратів (МНК). Оцінка параметрів лінійної
регресії за допомогою МНК.
Як знайти явний вид регресійної
залежності?
Треба знайти (оцінити) невідомі параметри цієї моделі та
Як це зробити?
Розглянемо приклад
Слайд 14Приклад
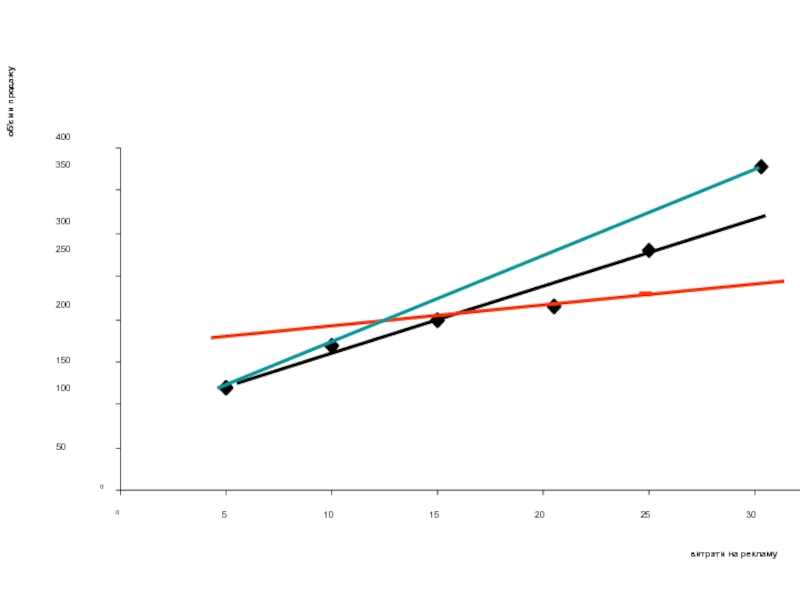
Підприємство вирішило проаналізувати зв’язок між витратами на рекламу продукції
та відповідними щомісячними об’ємами продаж цієї продукції. Для такої оцінки
зафіксовані дані за шість місяців діяльності.
Слайд 17Існує безліч прямих, які можна провести через дані точки
Яку пряму
обрати?
Обирають за критерієм мінімізації суми квадратів відхилень (застосовують метод найменших
квадратів - МНК)
Слайд 183. Оцінка параметрів лінійної регресії
проводиться за даними вибірки МНК
Оберемо
пряму
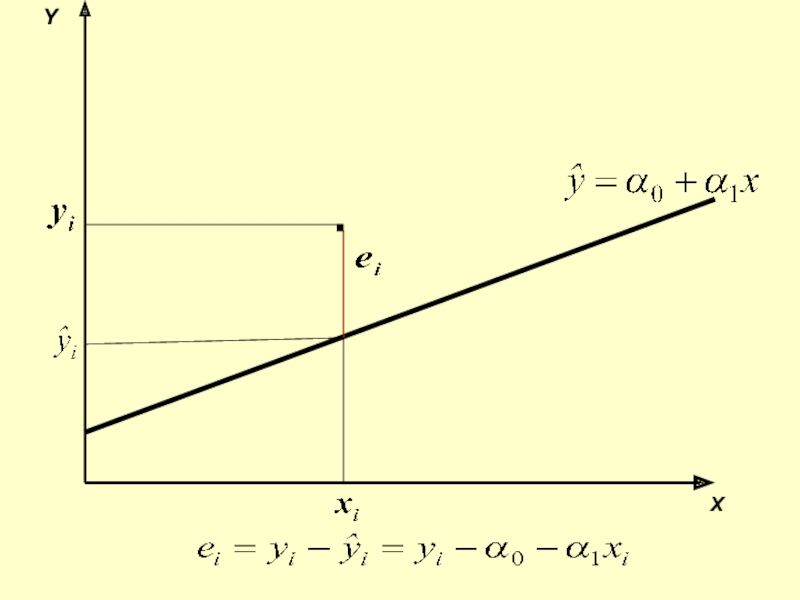
Слайд 20 Пряму треба проводити так, щоб сума квадратів помилок
була мінімальною, тобто:
Слайд 21Необхідною умовою існування мінімума неперервно диференційованої функції двох змінних є
рівність нулю її частинних похідних:
Слайд 22Остання система називається нормальною
Розв’язавши її, отримаємо
Слайд 24
вибірковий кореляційний момент випадкових величин X і Y.
вибіркова дисперсія Х
Слайд 25Коваріація - це статистична міра взаємодії двох змінних.
Наприклад, додатнє значення
коваріації прибутковості двох цінних паперів показує, що прибутковості цих ЦП
мають тенденцію змінюватись в одну сторону.
Дисперсія – ступінь розкиду значень змінних, але більш природно – середньоквадратичним відхиленням.
Слайд 26
3. Коефіцієнти кореляції та детермінації
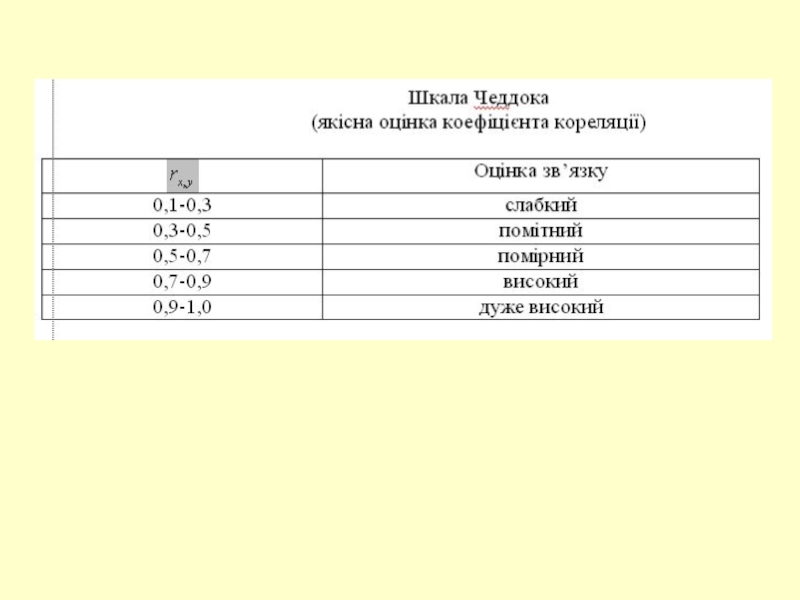
Слайд 27 Коефіцієнт кореляції
Для того, щоб оцінити щільність
зв’язку між змінними х та у, встановити значимість впливу змінної
х на у, слід обчислити коефіцієнт кореляції між х та у
Слайд 28Кореляційний аналіз
Виявлення взаємозв’язку між випадковими змінними, обчислення та перевірка значущості
множинних коефіцієнтів кореляції та детермінації
Відбір факторів, що найбільш впливають на
результативну ознаку
змінними прямий, при зростанні однієї величини, інша теж має тенденцію
зростати;
- зв’язок між змінними зворотній
-лінійного зв’язку між змінними
х та у немає взагалі або він дуже слабкий – це означає, що проста лінійна регресія не найкращим чином описує досліджуваний економічний об’єкт
Слайд 31
- існує сильний зв’язок
між змінними х та у
лінійна регресія досить точно описує поведінку досліджуваного економічного об’єкта
Слайд 33Коефіцієнт детермінації
Поряд з коефіцієнтом кореляції використовується для вимірювання щільності
зв’язку між двома та більше показниками
Є критерієм для перевірки
достовірності (адекватності) моделі – тобто дає відповідь на питання: чи справді у залежить від x, а не реалізується під впливом різноманітних випадкових факторів
Слайд 34Коефіцієнт детермінації обчислюється за формулою
Слайд 35Висновок
Якщо близький до 1,
то модель адекватна
Якщо близький
до нуля, то модель неадекватна
Показує, яка доля варіації ознаки Y враховано в моделі та обумовлена впливом на неї факторів.
Слайд 36
Кожна сума квадратів пов’язана з числом, яке називають її
ступенем вільності
Ступінь вільності суми квадратів показує скільки незалежних елементів інформації,
що утворилися з елементів
потрібно для розрахунку даної суми квадратів
4. Поняття про ступені вільності
Слайд 37Аналіз дисперсій (ANOVA - аналіз) у лінійній регресії (базова таблиця
дисперсійного аналізу)
Слайд 385. Перевірка моделі на адекватність
Якщо
близький до 1, то модель адекватна
Якщо
близький до нуля, то модель неадекватна
Якщо значення коефіцієнта детермінації має не явно виражене граничне значення
(наприклад, 0,5), то зробити однозначний висновок про адекватність моделі неможливо, тому….
Слайд 39В цьому випадку треба залучити статистичний критерій.
Найпоширенішим
з таких критеріїв є критерій Фішера (або F - критерій
)
Слайд 40Перевірка моделі на адекватність за допомогою F - критерія Фішера
Розраховуємо
F-відношення:
2. Задаємо рівень значущості
(рівнем значущості наз.
імовірність допустити помилку першого роду (імовірність відкинути правильну гіпотезу))
задають наперед ( 0,1; 0,05; 0,01)
Якщо - це означає, що правильну гіпотезу ми ризикуємо відкинути у 5-ти випадках зі 100 )
Слайд 413. За статистичними таблицями F-розподілу Фішера з (1, n-2)
ступенями вільності та рівнем значущості знаходимо критичне
значення критерію Фішера
Якщо ,то побудована нами регресійна модель адекватна реальній дійсності
Якщо ,то - неадекватна
Слайд 426. Критерій Стьюдента перевірки значимості параметрів моделі та коефіцієнта кореляції
генеральної сукупності.
Після визначення оцінок параметрів слід перевірити їх
статистичну надійність та істотність.
Слайд 431) t-тест Ст’юдента для перевірки на значимість параметрів , визначених
за методом найменших квадратів
ai – оцінка параметра
, отримана
за методом найменших квадратів;
- оцінка дисперсії параметра ai;
n – розмір вибірки.
Слайд 44За таблицями критичних точок розподілу Стьюдента за заданим рівнем значущості
і (п – т–1) ступенями свободи знаходимо
tкр ( , п – т – 1). Ураховуючи
двосторонню критичну область, порівнюємо tемп і tкр ( , п – т–1) та робимо відповідний статистичний висновок:
Якщо tемп < tкр ,тоді гіпотеза Н0 приймається та коефіцієнт є статистично незначущий.
Якщо tемп > tкр ,тоді гіпотеза Н0 відхиляється та коефіцієнт є статистично значущий.