Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение набора отрезков плоскости
Содержание
- 1. Пересечение набора отрезков плоскости
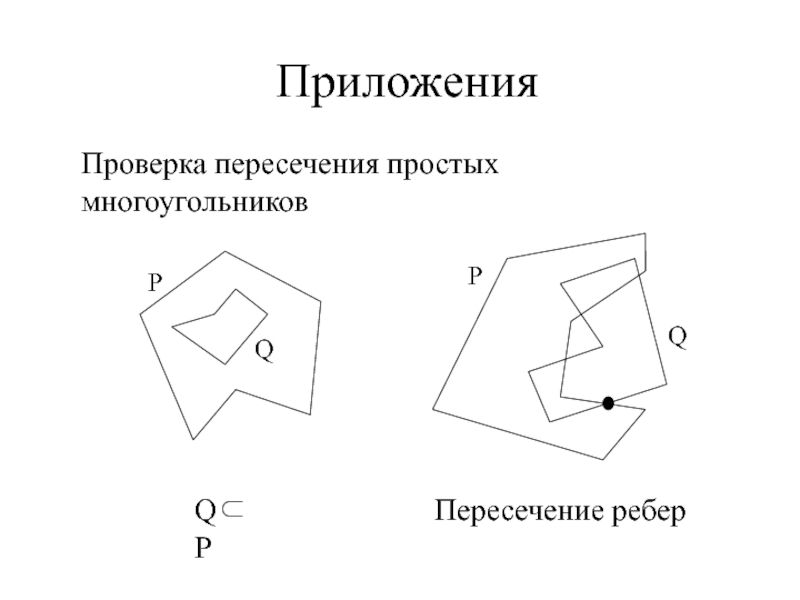
- 2. ПриложенияПроверка пересечения простых многоугольниковQ⊂PПересечение ребер
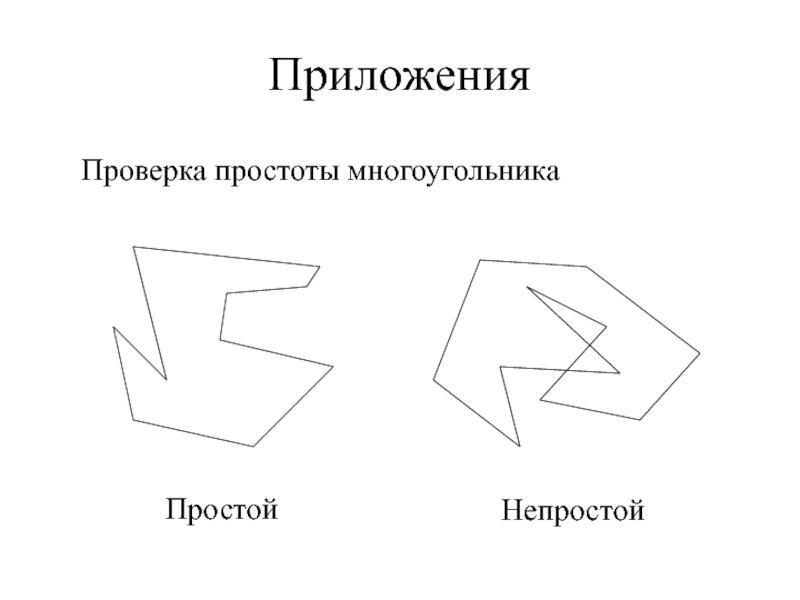
- 3. ПриложенияПроверка простоты многоугольникаПростойНепростой
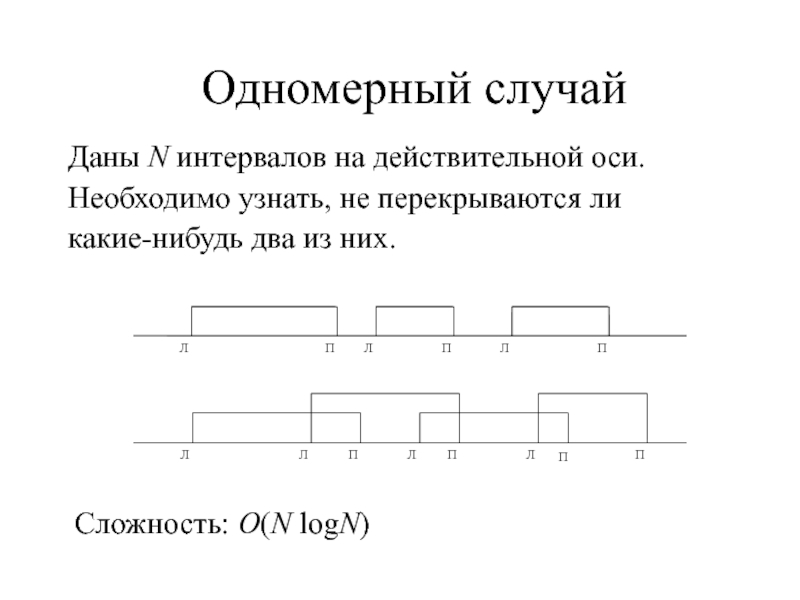
- 4. Одномерный случайДаны N интервалов на действительной оси.
- 5. Нижняя оценкаЗадача единственности элементовПроверка пересечения отрезковПреобразование задач:{xi}{[xi, xi]}Сложность задачи проверки пересечения отрезков: Θ(N logN)
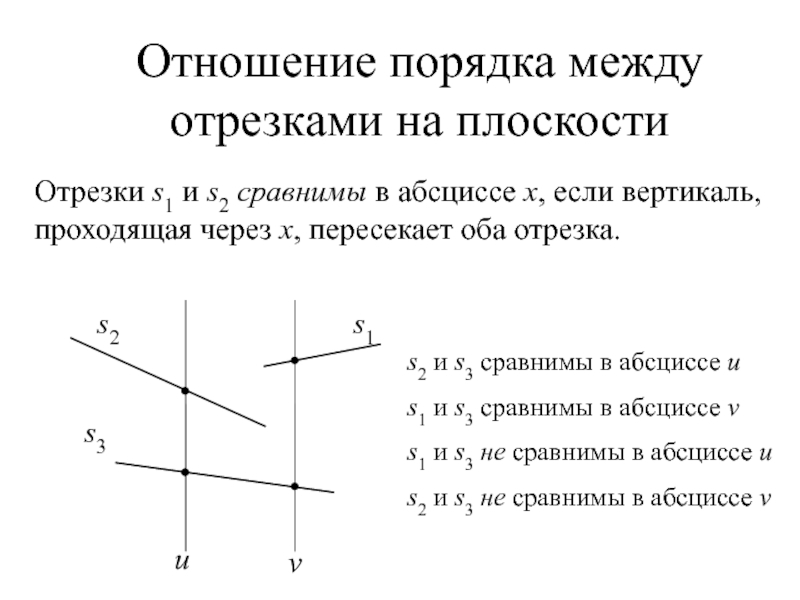
- 6. Отношение порядка между отрезками на плоскостиОтрезки s1
- 7. Отношение порядка между отрезками на плоскостиs2 >u
- 8. Метод плоского заметанияСтатус заметающей прямой: последовательность отрезков
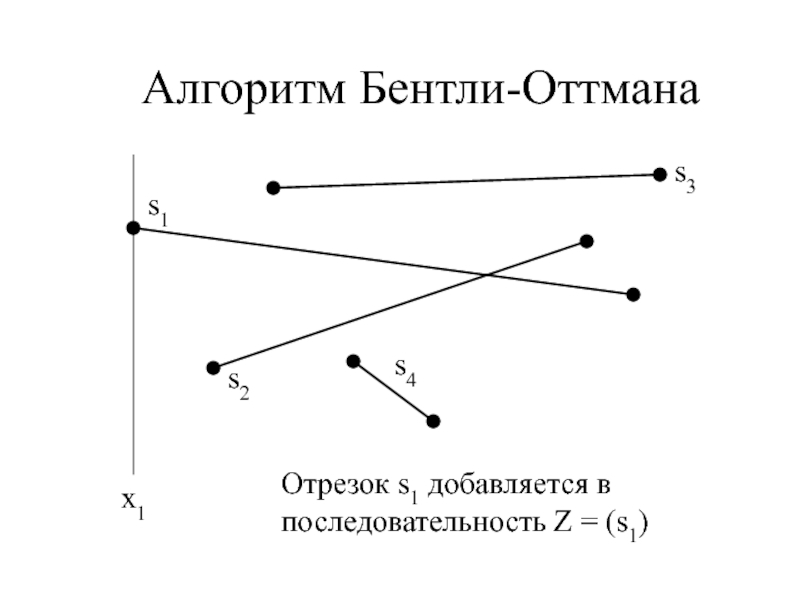
- 9. Алгоритм Бентли-Оттманаx1Отрезок s1 добавляется в последовательность Z = (s1)
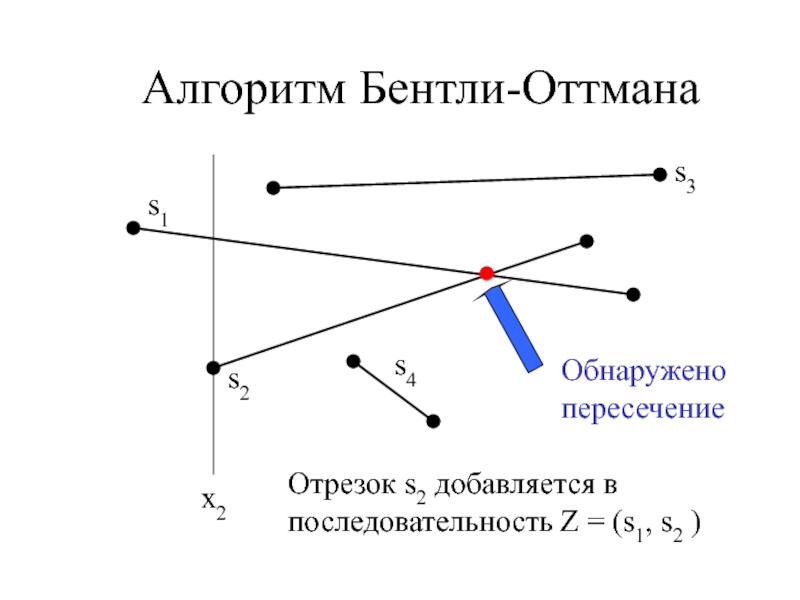
- 10. Алгоритм Бентли-Оттманаx2Отрезок s2 добавляется в последовательность Z = (s1, s2 )
- 11. Алгоритм Бентли-Оттманаx3Отрезок s3 добавляется в последовательностьZ = (s3, s1, s2)
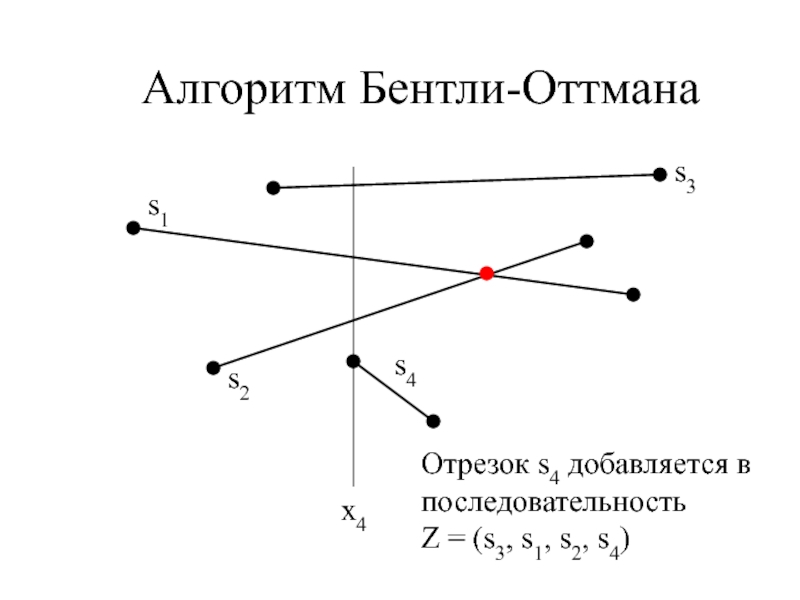
- 12. Алгоритм Бентли-Оттманаx4Отрезок s4 добавляется в последовательностьZ = (s3, s1, s2, s4)
- 13. Алгоритм Бентли-Оттманаx5Отрезок s4 удаляется из последовательностиZ = (s3, s1, s2)
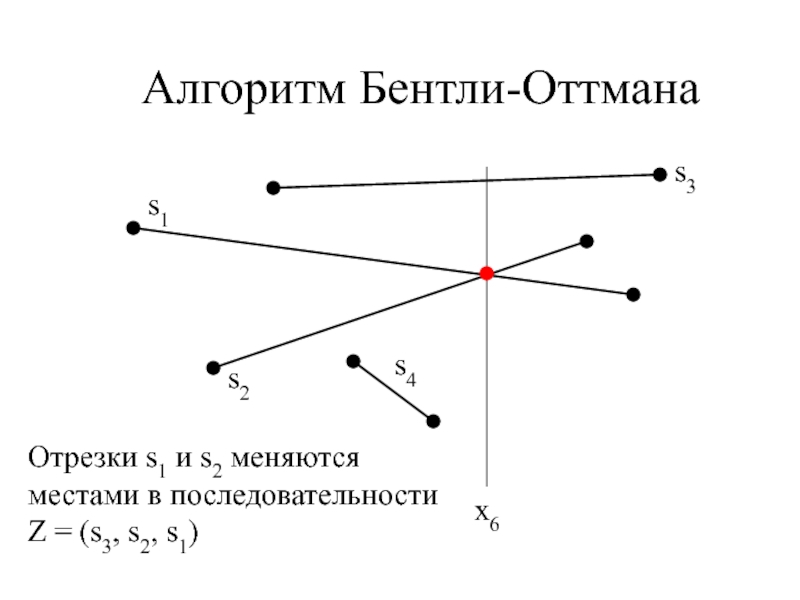
- 14. Алгоритм Бентли-Оттманаx6Отрезки s1 и s2 меняются местами в последовательностиZ = (s3, s2, s1)
- 15. Алгоритм Бентли-Оттманаx7Отрезок s2 удаляется из последовательностиZ = (s3, s1)
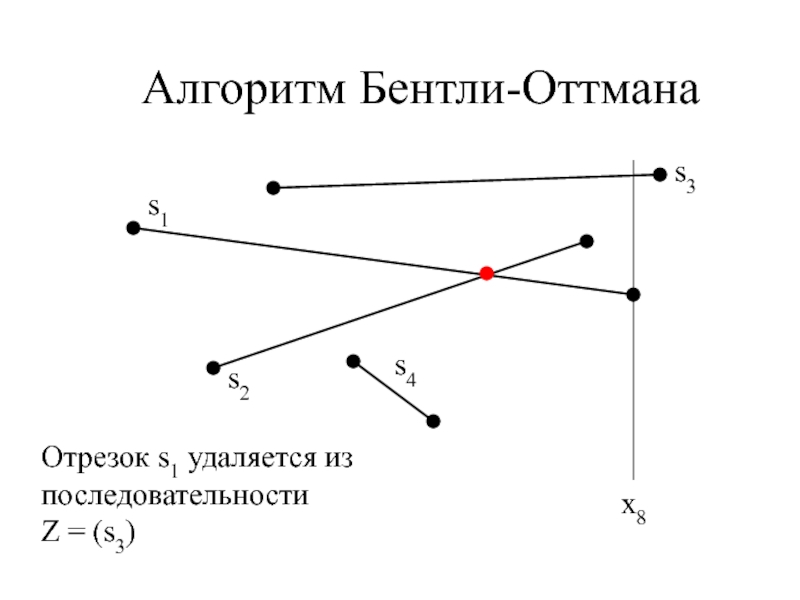
- 16. Алгоритм Бентли-Оттманаx8Отрезок s1 удаляется из последовательностиZ = (s3)
- 17. Алгоритм Бентли-Оттманаx9Отрезок s3 удаляется из последовательностиZ = ()
- 18. Оценка сложностиПоиск всех пересечений Ω(K+NlogN)Проверка пересечения Θ(NlogN)
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Пересечение набора отрезков на плоскости
Даны N прямолинейных отрезков на плоскости
Задача
1: Поиск всех пересечений отрезков
двух отрезковСлайд 4Одномерный случай
Даны N интервалов на действительной оси. Необходимо узнать, не
перекрываются ли какие-нибудь два из них.
Сложность: O(N logN)
Слайд 5Нижняя оценка
Задача единственности элементов
Проверка пересечения отрезков
Преобразование задач:
{xi}
{[xi, xi]}
Сложность задачи проверки
пересечения отрезков: Θ(N logN)
Слайд 6Отношение порядка между отрезками на плоскости
Отрезки s1 и s2 сравнимы
в абсциссе x, если вертикаль, проходящая через x, пересекает оба
отрезка.u
v
s2 и s3 сравнимы в абсциссе u
s1 и s3 сравнимы в абсциссе v
s1 и s3 не сравнимы в абсциссе u
s2 и s3 не сравнимы в абсциссе v
Слайд 7Отношение порядка между отрезками на плоскости
s2 >u s4, s1 >v
s2, s2 >v s4, s1 >v s4
s3 не сравним ни
с каким другим отрезкомОтрезок s1 выше отрезка s2 в х (пишется s1 >x s2), если s1 и s2 сравнимы в х, и точка пересечения s1 с вертикалью x лежит выше точки пересечения s2 с ней же.

![Пересечение набора отрезков плоскости Нижняя оценкаЗадача единственности элементовПроверка пересечения отрезковПреобразование задач:{xi}{[xi, xi]}Сложность задачи проверки пересечения отрезков: Θ(N logN) Нижняя оценкаЗадача единственности элементовПроверка пересечения отрезковПреобразование задач:{xi}{[xi, xi]}Сложность задачи проверки пересечения отрезков: Θ(N logN)](/img/thumbs/507db41f325fa024927e45535ff78285-800x.jpg)