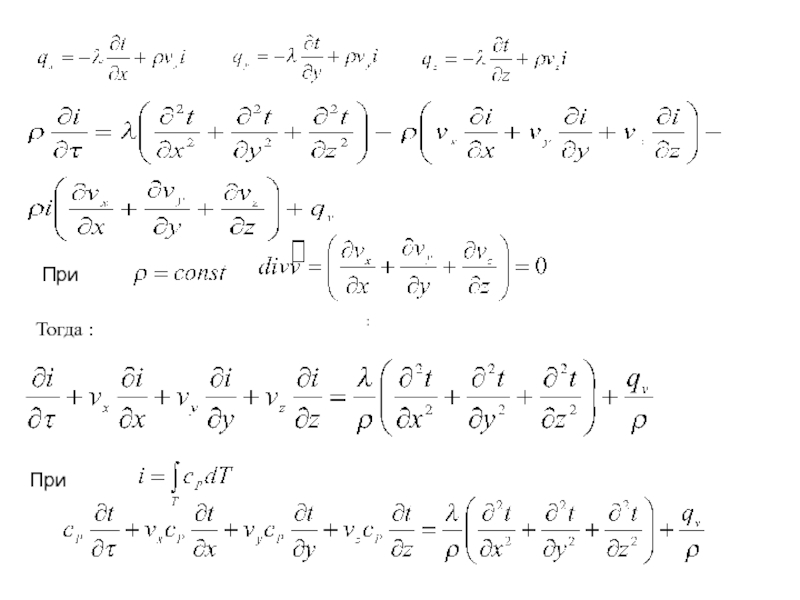КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

Конвективный теплообмен возможен только в движущейся среде, в которой перенос

теплоты неразрывно связан с переносом самой массы. Если движение жидкости (газа) вызвано какими-то внешними побудителями (насосом, вентилятором и т.д.), конвекцию называют вынужденной. Если же движение жидкости (газа) возникает под действием неоднородного поля массовых сил (например, гравитационных), то такой процесс принято называть свободной или естественной конвекцией. Отличительной особенностью конвективного теплообмена является передача теплоты двумя механизмами одновременно – теплопроводностью и конвекцией.
Различают так называемые внутренние задачи (теплообмен между стенками канала и потоком теплоносителя в нем) и задачи при внешнем обтекании тел.

Пусть в единицу времени через единицу поверхности нормально к ней проходит масса жидкости

, то она переносит тепловой поток плотностью:

где

– энтальпия массы вещества.

Т.к. конвекция всегда сопровождается теплопроводностью, то конвективный теплообмен можно описать уравнением:

теплоты от жидкости к элементу
поверхности тела;

– коэффициент теплоотдачи или коэффициент конвективного теплообмена.

Коэффициент конвективного теплообмена зависит от формы и размеров тел, скорости, температуры и физических параметров движущейся среды (коэффициента теплопроводности

удельной теплоемкости

плотности

коэффициента температуропроводности

коэффициента вязкости.
Из курса Гидравлики известно, что все реальные жидкости обладают вязкостью. Вязкостью называется свойство среды оказывать сопротивление сдвигающим усилиям при относительном движении слоев. Между слоями жидкости или газа при их относительном движении возникает сила вязкости или внутреннего трения, определяемая формулой Ньютона:

вязкости – это касательная сила, отнесенная к единице поверхности, которая

действует в любой точке потока в плоскости, ориентированной по течению, пропорциональна изменению скорости по нормали к этой плоскости.
Кроме динамического коэффициента вязкости

используют кинематический коэффициент вязкости (м2/c):

Коэффициенты

и

сильно зависят от температуры и слабо от давления.

от давления в жидкостях становится существенной при давлениях

.

Зависимость

При течении жидкости или газа наличие внутреннего трения проводит к рассеиванию энергии. При этом часть кинетической энергии жидкости необратимо переходит в теплоту и вызывает нагрев жидкости.
На теплоотдачу влияет сжимаемость жидкости, которая характеризуется изотермическим коэффициентом сжимаемости:

Для идеальных газов

Сжимаемость сплошных сред может быть описана обобщенным законом Гука:

жидкостей изотермической сжимаемостью можно пренебречь. В газах существенным является отношение

разности давлений к абсолютному давлению среды. Если это отношение мало, то такие потоки считаются несжимаемыми.
В конвективном теплообмене существенную роль играет тепловое расширение жидкости, которое характеризуется коэффициентом объемного расширения (отношение изменения объема к разности температур при постоянном давлении):

Для

сравнительно мал. Для некоторых жидкостей

может иметь отрицательное значение, например у воды при

Для газов коэффициент объемного расширения практически одинаков. С достаточной степенью точности можно считать его равным коэффициенту объемного расширения идеального газа, для которого известна формула:

жидкостей коэффициент

<4°C.

и изотропна, физические параметры жидкости постоянны. Выделим в потоке жидкости

неподвижный параллелепипед с размерами

К выводу дифференциального уравнения энергии

Через грани параллелепипеда теплоты переносится теплопроводностью и конвекцией. Аналогично выводу дифференциального уравнения теплопроводности имеем:

где

– энтальпия реальной жидкости;

Учитывая, что:

– плотность теплового потока за счет, соответственно теплопроводности и конвекции; то:

скорости
.
Таким образом,
характеризует изменение температуры во времени
в какой-либо

точке жидкости, т.е. является локальным изменением температуры.

Величина

представляет собой изменение

температуры при переходе от одной точки к другой, т.е. является конвективным изменением температуры.

Обозначая

, уравнение энергии запишем в виде:

дифференциального уравнения движения был рассмотрен в курсе Гидравлики, приводим известную

систему уравнений движения Навье – Стокса:

в какой-либо точке
жидкости (локальное ускорение), а
– изменение скорости
при переходе

от точки к точке, т.е. конвективное ускорение. Отсюда уравнение Навье-Стокса можно записать в виде:

Из определения коэффициента объемного расширения и учитывая, что величина

, имеем:

После преобразований:
При этом выражение
можно рассматривать как сумму

сил тяжести при определенной плотности

Величину

представим как градиент гидростатического давления

в жидкости с плотностью

Отсюда

Где

и тогда:

и подъемной силы

уравнением неразрывности для однородной несжимаемой жидкости в следующем виде:
Краевые условия

однозначности состоят из геометрических, временных или начальных, физических и граничных условий.

теплообмена при движении среды в трубе зависит от режима течения,

для определения которого используют известный критерий Рейнольдса

– средняя скорость движения жидкости,

– внутренний диаметр трубы,

– кинематическая вязкость

течение считается ламинарным. При достижении

в трубе устанавливается турбулентный режим движения жидкости.

Далее по мере формирования стабилизированного течения

стремится к постоянной величине.

:

При

На входе в трубу коэффициент теплоотдачи

имеет максимальное значение.

Известно, что при ламинарном изотермическом режиме течения распределение скорости носит параболический характер, причем средняя скорость составляет

движении неизотермического потока различают вязкостный и вязкостно-гравитационный режимы. Вязкостный режим

соответствует течению жидкости при отсутствии естественной конвекции. Передача теплоты в этом случае осуществляется только теплопроводностью. Вязкостно-гравитационный режим имеет место тогда, когда вынужденное течение жидкости сопровождается свободной конвекцией. Соответственно передача теплоты осуществляется теплопроводностью и конвекцией.
Распределение скоростей при вязкостном режиме зависит от направления теплового потока. При нагревании жидкости скорость и теплоотдача у стенок больше, чем при охлаждении.
Теплообмен при вязкостно-гравитационном режиме зависит от взаимного направления вынужденного движения и свободной конвекции. В большинстве случаев при совпадении этих направлений скорости у стенки возрастают, а теплоотдача уменьшается. При взаимно перпендикулярном направлении естественной и вынужденной конвекции теплоотдача увеличивается. Аналитического решения теплоотдачи при ламинарном режиме до настоящего времени не получено. Для определения коэффициента теплоотдачи пользуются эмпирическими формулами.

потока имеет вид усеченной параболы. Наиболее резкое изменение скоростей наблюдается

у стенок в пределах пограничного слоя, максимальная скорость – на оси трубы. В практических расчетах пользуются средними значениями скоростей:

– расход жидкости;

– площадь поперечного сечения трубы.

Отношение средней скорости к максимальной при турбулентном режиме является функцией

:

В турбулентном потоке в связи с интенсивным перемешиванием жидкости естественная конвекция не оказывает существенного влияния на теплоотдачу.

Теплоотдача при переходном режиме

зависит

от большого числа факторов, то для определения коэффициента теплоотдачи пользуются эмпирическими формулами.

плоская поверхность пластины омывается безграничным потоком с равномерным распределением скоростей,

то начиная с передней кромки пластины, на ней образуется гидродинамический пограничный слой, в котором скорость изменяется от 0 на стенке до скорости невозмущенного потока. При этом режим течения в пограничном слое может быть как ламинарным, так и турбулентным. Режим течения в пограничном слое изотермического потока считают ламинарным при

а в неизотермических – при

В неизотермических потоках образуется помимо гидродинамического тепловой пограничный слой, в котором температура потока изменяется от температуры поверхности пластины до температуры потока вдали от пластины. Коэффициент теплоотдачи зависит от режима течения, свойств жидкости, интенсивности и направления теплового потока.

Рассмотрим теплоотдачу при поперечном обтекании жидкостью одиночной трубы (рис.).

теплоотдачи.
теплоотдачи от угла
По оси ординат отложены относительные значения

коэффициента теплоотдачи

, отсчитываемого

,

- соответственно среднее

и

При

(в лобовой части трубы) коэффициент теплоотдачи

имеет наибольшее значение, т.к. пограничный слой имеет минимальную толщину.

С увеличением толщины пограничного слоя коэффициент теплоотдачи уменьшается, достигая минимума в окрестности экватора при

Затем происходит разрушение пограничного слоя и увеличение коэффициента теплоотдачи. Такая картина получена при

Изменение интенсивности теплоотдачи в зависимости от угла

становится процесс обтекания пучка труб, что имеет место в различных

теплообменных аппаратах. На практике применяются два вида расположения труб в пучке – коридорное и шахматное. Основные характеристики пучка труб:
– внешний диаметр;
– количество рядов труб по ходу движения жидкости;
– шаг в продольном и поперечном направлении.

Режим течения в теплообменниках зависит от условий на входе. Наиболее изученным является так называемый смешанный режим, когда на входе в лобовой части имеет место ламинарный режим, а в межтрубном пространстве и на выходе – турбулентный. Характер обтекания первого ряда трубок аналогичен обтеканию одиночной трубы. При коридорном расположении трубы каждого последующего ряда затеняются трубами предыдущего, что ухудшает условия обтекания. При шахматном расположении подобное затенение отсутствует. В связи с этим коэффициент теплоотдачи при шахматном расположении труб выше, чем при коридорном, что наглядно видно на рис. для 7-рядных теплообменников.

(б) расположения труб

два максимума при углах порядка 50-60° к направлению потока. Откуда

можно сделать вывод, что на входе и на выходе теплоотдача при коридорном расположении меньше, чем у одиночной трубы. При любом расположении труб каждый ряд вызывает усиление турбулизации потока, поэтому коэффициент теплоотдачи второго ряда больше, чем первого, а для третьего больше, чем для второго. Затем поток стабилизируется, и коэффициент теплоотдачи для всех последующих рядов становится постоянным. Конвективный теплообмен в свободном потоке возникает в связи с изменением плотности жидкости при нагревании, например, у нагретых печей, трубопроводов и приборов систем отопления. Слои жидкости, нагреваясь, под действием гравитационной силы поднимаются вверх, а на их место поступает более холодная жидкость из окружающего пространства. Нисходящие конвективные потоки возникают вблизи охлажденных поверхностей. Рассмотрим свободный теплообмен в неограниченном пространстве вблизи вертикальной нагретой поверхности. Характер возникающего конвективного течения определяется длиной поверхности теплообмена и температурным напором – разностью между температурами стенки и жидкости. На рис. приведена схема свободного конвективного теплообмена у вертикальной стенки.

стенки (1-1) наблюдается увеличение толщины пограничного слоя
а режим течения

носит ламинарный характер. Затем на некотором удалении от кромки течение приобретает локонообразный характер, при этом ламинарный пограничный слой начинает разрушаться (2-2). Локонообразное течение переходит в развитое турбулентное течение с ламинарным подслоем вблизи поверхности стенки. Толщина пограничного слоя и особенности режима течения жидкости определяют характер изменения коэффициента теплоотдачи. На участке 1-2 коэффициента теплоотдачи уменьшается до минимального значения при максимальной толщине пограничного слоя.

В области локонообразного течения (2-3) коэффициент теплоотдачи возрастает и достигает постоянного максимального значения в области развитого турбулентного течения. Кроме высоты стенки на величину коэффициента теплоотдачи существенное влияние оказывают форма тела, физические параметры жидкости и изменение температурного напора по высоте пластины.

стационарного теплового потока и регулярного теплового режима.
Метод стационарного теплового потока

основан на законе Ньютона

, откуда местный коэффициент теплоотдачи определяется:

Среднее значение коэффициента теплоотдачи:

Если изменение коэффициента теплоотдачи происходит в одном направлении, например по длине канала, то можно записать в виде:

потока:
где
– соответственно общий тепловой поток (Вт) и площадь
поверхности (м2).

Тогда:

Средний температурный напор:

Для нахождения среднего температурного напора на практике в зависимости от характера изменения температуры применяют несколько выражений. При незначительном изменении температуры жидкости в канале используют среднее арифметическое значение:

– средние по сечению температуры жидкости соответственно на входе и на выходе из канала.

значений в отдельных точках поверхности. В общем случае средний температурный

напор между температурами стенки и жидкости определяют по логарифмическому закону:

На практике для одной и той же задачи могут быть приняты различные температуры. Например, при течении жидкости в трубах за расчетную принимают среднюю температуру жидкости в сечении и температуру жидкости на входе в трубу. В зависимости от выбора так называемой «определяющей» температуры различны будут и значения коэффициента теплоотдачи.

В общем случае температура и скорость движения жидкости переменны по сечению потока. Выделим в поперечном сечении канала элементарную площадку

площадку
будет равен
выражение для теплового потока примет вид:
Интегрируя по всему

сечению, получим:

Выбираем среднее значение энтальпии

так, чтобы выполнялось

равенство:

Откуда:

среднемассовой по сечению температурой потока.
При
и
эта температура может

быть

определена по формуле:

– объемный расход жидкости.

Рассмотрим определение теплового потока по балансу энергии жидкости в ламинарном течении несжимаемой жидкости в плоской щели. Пусть поле скоростей симметрично относительно оси

Рис. К определению теплового потока по балансу энергии жидкости

имеем:
Или
Умножив это уравнение почленно на
и проинтегрировав в пределах

от

до

получим:

в правой части равен:
Учитывая, что переменные
- независимые, можно

изменить

порядок их дифференцирования и интегрирования. В результате для определения плотности теплового потока через стенку получим выражение:

площади поперечного сечения
получим:
Тогда тепловой поток, проходящий через стенки трубы

длиной

находится следующим образом:

можно записать в виде:
Тогда:
Поскольку
то можно записать:
При

использовании метода регулярного теплового режима средний коэффициент теплоотдачи определяется:
–

полная теплоемкость тела;

- коэффициент неравномерности распределения температуры в теле.

При

- темп охлаждения соответственно текущий и при

;

теплоотдачи методом регулярного теплового режима экспериментально определяется только темп охлаждения.

Измерять температуру тела не требуется, что особенно актуально для тел сложной формы. Однако метод имеет ограничения из-за асимптотического характера зависимости темпа охлаждения от коэффициента теплоотдачи.
При использовании метода квазистационарного режима нагрева расчетная зависимость находится из закона Ньютона после подстановки в него плотности теплового потока:

- коэффициент, учитывающий форму тела

1, 2, 3 соответственно для пластины,

цилиндра и шара

- половина толщины пластины, радиус цилиндра и шара;

– скорость нагрева

В опытах измеряют скорость нагрева и температурный напор.