Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ЛИНЕЙНАЯ АЛГЕБРА
Содержание
- 1. ЛИНЕЙНАЯ АЛГЕБРА
- 2. 1. Линейные пространстваРассматриваемые вопросы:1.1. Понятие линейного пространства1.2. Линейная
- 3. 1.1. Понятие линейного пространства 1.1.1. Определение линейного
- 4. © Веденяпин Е.Н. 2013Определение сложения и умножения
- 5. © Веденяпин Е.Н. 20131.1.2. Аксиомы сложения и
- 6. © Веденяпин Е.Н. 2013Аксиомы сложения и умножения
- 7. © Веденяпин Е.Н. 2013ЗамечанияЭлементы линейного пространства называются
- 8. © Веденяпин Е.Н. 20131.1.3. Свойства линейного пространстваСвойство
- 9. © Веденяпин Е.Н. 2013Свойство 2. Единственность противоположного
- 10. © Веденяпин Е.Н. 2013Свойство 3. ДоказательствоПрибавляя к
- 11. © Веденяпин Е.Н. 2013Свойство 4. ДоказательствоПрибавляя к
- 12. © Веденяпин Е.Н. 2013Свойство 5. Если произведение
- 13. © Веденяпин Е.Н. 20131.1.4. Примеры линейных пространствПример
- 14. © Веденяпин Е.Н. 2013Пример 2. Множество всех
- 15. © Веденяпин Е.Н. 2013Пример 3 Рассмотрим множество
- 16. © Веденяпин Е.Н. 2013Пример 3 (окончание) Операции
- 17. © Веденяпин Е.Н. 2013Пример 4. Множество многочленов
- 18. © Веденяпин Е.Н. 20131.1.5. Линейное подпространствоПусть множество
- 19. © Веденяпин Е.Н. 2013Проверка выполнимости аксиом линейного
- 20. © Веденяпин Е.Н. 2013Проверка выполнимости 3 аксиомы
- 21. 1.2. Линейная независимость векторов 1.2.1. Определение линейной зависимостиПусть
- 22. © Веденяпин Е.Н. 20131.2.2. Линейные комбинации векторовПусть
- 23. © Веденяпин Е.Н. 2013Определение линейной комбинации векторовПолучаем
- 24. © Веденяпин Е.Н. 20131.2.3. Линейная комбинация и
- 25. © Веденяпин Е.Н. 2013Примеры линейной зависимости векторовПример
- 26. © Веденяпин Е.Н. 20131.2.4. Размерность линейного пространстваЛинейное
- 27. 1.3. Базис линейного пространства1.3.1. Определение базиса линейного
- 28. © Веденяпин Е.Н. 20131.3.2. Теорема о представлении
- 29. © Веденяпин Е.Н. 20131.3.3. Координаты вектора Пусть
- 30. © Веденяпин Е.Н. 2013Равенство векторовИз приведенной теоремы
- 31. © Веденяпин Е.Н. 20131.3.4. Операции над векторами
- 32. © Веденяпин Е.Н. 2013Умножение вектора на числоРассмотрим
- 33. Если векторы пространства Ln заданы своими координатами
- 34. © Веденяпин Е.Н. 20131.3.5. Линейные комбинации векторов в координатной форме Пусть дана линейная комбинация векторовгде
- 35. © Веденяпин Е.Н. 2013Линейные комбинации векторов в
- 36. © Веденяпин Е.Н. 20131.3.6. Координаты нулевого вектораУ
- 37. © Веденяпин Е.Н. 20131.3.7. Координаты противоположного вектораВектор, противоположный векторуравенДоказательство
- 38. 1.4. Примеры базисов линейных пространств1.4.1. Трехмерное пространствоДля
- 39. © Веденяпин Е.Н. 20131.4.2. n-мерное пространствоПусть имеется
- 40. © Веденяпин Е.Н. 2013Определение координат вектораНайдем координаты
- 41. © Веденяпин Е.Н. 20131.4.3. Пространство многочленов степени
- 42. © Веденяпин Е.Н. 2013Представление многочлена в выбранном
- 43. 2. Преобразование координат при замене базиса Рассматриваемые
- 44. 2.1. Замена базиса в трехмерном пространстве 2.1.1. Изменение
- 45. © Веденяпин Е.Н. 2013Матрица переходаБазисные вектора нового
- 46. © Веденяпин Е.Н. 2013Матричная форма записиИспользуя матрицу
- 47. © Веденяпин Е.Н. 2013Обратный переходПоскольку базисные вектора
- 48. © Веденяпин Е.Н. 20132.1.2. Связь между координатами
- 49. © Веденяпин Е.Н. 2013Преобразование координат вектора при
- 50. © Веденяпин Е.Н. 20132.1.3. Связь между координатами
- 51. © Веденяпин Е.Н. 20132.1.4. Изменение системы координат
- 52. © Веденяпин Е.Н. 2013Закон преобразования координат точки
- 53. © Веденяпин Е.Н. 2013Закон преобразования координат точки
- 54. © Веденяпин Е.Н. 20132.1.5. Изменение системы координат
- 55. © Веденяпин Е.Н. 2013Частный случай декартовых прямоугольных
- 56. 2.2. Пример замены базиса в трехмерном пространстве 2.2.1.
- 57. © Веденяпин Е.Н. 2013Постановка задачи (окончание)Доказать, что
- 58. © Веденяпин Е.Н. 20132.2.2. Проверка линейной независимости
- 59. © Веденяпин Е.Н. 2013Проверка линейной независимости векторов
- 60. © Веденяпин Е.Н. 2013Проверка линейной независимости векторов
- 61. © Веденяпин Е.Н. 20132.2.3. Нахождение вектора b
- 62. © Веденяпин Е.Н. 2013Обратная матрица переходаПоскольку матрица
- 63. © Веденяпин Е.Н. 2013Координаты вектора b в новом базисеКоординаты вектора b в базисе а1, а2, а3
- 64. © Веденяпин Е.Н. 20132.2.4. Нахождение связи между
- 65. © Веденяпин Е.Н. 2013Нахождение связи между базисами е1, е2, е3 и а1, а2, а3 (окончание)
- 66. 2.3. Замена базиса в n-мерном пространстве 2.3.1. Матрица
- 67. © Веденяпин Е.Н. 2013Матрица перехода от старого
- 68. © Веденяпин Е.Н. 2013Матрица перехода от нового
- 69. © Веденяпин Е.Н. 20132.3.2. Последовательная замена нескольких
- 70. © Веденяпин Е.Н. 20134.3.3. Матрица перехода к
- 71. © Веденяпин Е.Н. 20132.3.4. Компоненты вектора в
- 72. © Веденяпин Е.Н. 2013Компоненты вектора в различных
- 73. 4.4. Изоморфизм линейных пространств 2.4.1. Определение изоморфизмаЛинейные пространства
- 74. © Веденяпин Е.Н. 20132.4.2. Следствие из определения
- 75. © Веденяпин Е.Н. 20132.4.3. Изоморфизм пространств одинаковой
- 76. 3. Линейные подпространства Рассматриваемые вопросы:3.1. Линейные подпространства3.2.
- 77. 3.1. Линейные подпространства 3.1.1. Определение линейного подпространстваПусть имеется
- 78. © Веденяпин Е.Н. 20133.1.2. Примеры линейных подпространствПример
- 79. © Веденяпин Е.Н. 2013Пример 2Линейное пространство R1
- 80. © Веденяпин Е.Н. 2013Пример 3Линейное пространство R2
- 81. © Веденяпин Е.Н. 2013Пример 4В геометрическом пространстве
- 82. 3.2. Сумма и пересечение линейных подпространств3.2.1. Сумма
- 83. © Веденяпин Е.Н. 2013Пример суммы подпространствКаждый вектор
- 84. © Веденяпин Е.Н. 20133.2.2. Пересечение линейных подпространствПересечением
- 85. © Веденяпин Е.Н. 2013Пример пересечения подпространствРассмотрим подпространства
- 86. 3.3. Свойства суммы и пересечения линейных подпространств3.3.1.
- 87. © Веденяпин Е.Н. 20133.3.2. Второе свойство суммы
- 88. 3.4. Линейная оболочка3.4.1. Определение линейной оболочкиЛинейной оболочкой
- 89. © Веденяпин Е.Н. 2013Пример линейной оболочки
- 90. 4. Евклидово пространство Рассматриваемые вопросы:4.1. Евклидово пространство4.2.
- 91. 4.1. Евклидово пространство 4.1.1. Определение евклидова пространстваn –
- 92. © Веденяпин Е.Н. 2013ЕвклидЕВКЛИД(ок. 300 г. до н.э.)
- 93. © Веденяпин Е.Н. 2013Аксиомы скалярного произведенияСкалярное произведение
- 94. © Веденяпин Е.Н. 2013Следствие из аксиом скалярного
- 95. © Веденяпин Е.Н. 20134.1.2. Первый пример евклидового
- 96. © Веденяпин Е.Н. 20134.1.3. Второй пример евклидового
- 97. © Веденяпин Е.Н. 2013Пример 2 (продолжение)Найдем условия,
- 98. © Веденяпин Е.Н. 2013Пример 2 (продолжение)Для выполнения
- 99. © Веденяпин Е.Н. 2013Пример 2 (окончание)Квадратичная форма
- 100. © Веденяпин Е.Н. 2013Условия, при которых матрица
- 101. © Веденяпин Е.Н. 2013Частный случайЕсли в качестве
- 102. 4.2. Длина вектора и угол между векторами 4.2.1.
- 103. © Веденяпин Е.Н. 20134.2.2. Теорема ПифагораВекторы x
- 104. © Веденяпин Е.Н. 2013ПифагорПИФАГОРСамосский(570 – 490 г.г. до н.э.)
- 105. © Веденяпин Е.Н. 20134.2.3. Угол между векторамиУгол
- 106. © Веденяпин Е.Н. 2013ПримерНайти угол между векторами а и b в четырехмерном пространстве, если
- 107. © Веденяпин Е.Н. 20134.2.4. Неравенство Коши-БуняковскогоВ любом
- 108. © Веденяпин Е.Н. 2013Коши и БуняковскийОгюстен ЛуиКОШИ(1789 – 1857)Виктор Яковлевич БУНЯКОВСКИЙ(1804 – 1889)
- 109. 4.3. Ортонормированная система векторов 4.3.1. Нормированный векторНенулевой вектор
- 110. © Веденяпин Е.Н. 20134.3.2. Нормирующий множительЛюбой ненулевой
- 111. © Веденяпин Е.Н. 2013ПримерНайти нормирующий множитель для вектора а, еслиПостроить нормированный вектор.
- 112. © Веденяпин Е.Н. 20134.3.3. Ортонормированная система векторовСистема
- 113. © Веденяпин Е.Н. 20134.3.4. Теорема о линейной
- 114. © Веденяпин Е.Н. 2013Доказательство (продолжение)Покажем, что векторное
- 115. © Веденяпин Е.Н. 2013Доказательство (окончание)Из условия ортогональности
- 116. 4.4. Процесс ортогонализации векторов 4.4.1. Суть процесса ортогонализацииРассмотрим
- 117. © Веденяпин Е.Н. 20134.4.2. Первый шаг процедуры
- 118. © Веденяпин Е.Н. 20134.4.3. Последующие шаги процедуры
- 119. © Веденяпин Е.Н. 2013Последующие шаги процедуры ортогонализации
- 120. © Веденяпин Е.Н. 2013Последующие шаги процедуры ортогонализации
- 121. © Веденяпин Е.Н. 2013Последующие шаги процедуры ортогонализации
- 122. © Веденяпин Е.Н. 20134.4.4. Неравенство нулю вектора
- 123. © Веденяпин Е.Н. 20134.4.5. Заключительные замечанияПо векторам
- 124. 6.5. Построение ортонормированного базиса 6.5.1. Теорема о существовании
- 125. © Веденяпин Е.Н. 20134.5.2. Пример построения ортонормированного
- 126. © Веденяпин Е.Н. 2013Построение вектора b2Вектор b2 будем искать в видегдеТогда
- 127. © Веденяпин Е.Н. 2013Построение вектора b3Вектор b3 будем искать в видегдеТогда
- 128. © Веденяпин Е.Н. 2013Вычисление норм векторов b1, b2, b3Находим нормы векторов b1, b2, b3
- 129. © Веденяпин Е.Н. 2013Построение ортонормированного базисаНормируем векторы b1, b2, b3. Получим ортонормированный базис
- 130. © Веденяпин Е.Н. 20134.5.3. Координатное представление скалярного
- 131. © Веденяпин Е.Н. 2013Скалярное произведение в ортонормированном базисеПусть– ортонормированный базис.Следовательно,Тогда скалярное произведение векторов представляется в виде
- 132. © Веденяпин Е.Н. 2013Обратное утверждениеЕсли в базисе
- 133. © Веденяпин Е.Н. 20134.5.4. Ортогональная проекция вектораПусть
- 134. © Веденяпин Е.Н. 20136.5.5. Расстояние между векторамиРасстояние
- 135. © Веденяпин Е.Н. 2013Свойства расстоянияИз определения расстояния следует, что:
- 136. © Веденяпин Е.Н. 2013СПАСИБО ЗА ВНИМАНИЕ!
- 137. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1© Веденяпин Е.Н. 2013
ЛИНЕЙНАЯ АЛГЕБРА
Проф.
ВЕДЕНЯПИН
Евгений Николаевич
Евразийский открытый институт
Кафедра естественнонаучных, математических
и общетехнических дисциплин
Слайд 2 1. Линейные пространства
Рассматриваемые вопросы:
1.1. Понятие линейного пространства
1.2. Линейная независимость векторов
1.3. Базис
линейного пространства
1.4. Примеры базисов линейных пространств
© Веденяпин Е.Н. 2013
Слайд 31.1. Понятие линейного пространства
1.1.1. Определение линейного пространства
Множество L элементов
любой природы
называется линейным (векторным) пространством, если для элементов этого
пространства определены операции сложения и умножения на число.© Веденяпин Е.Н. 2013
Слайд 4© Веденяпин Е.Н. 2013
Определение сложения и умножения на число
Сложение
Любой паре
элементов , ставится в
однозначное соответствие элемент , называемый суммой и обозначаемыйУмножение на число
Каждому элементу этого пространства и любому числу ставится в однозначное соответствие элемент , называемый произведением элемента на число и обозначаемый
Слайд 5© Веденяпин Е.Н. 2013
1.1.2. Аксиомы сложения и умножения на число
Коммутативность
сложения
Ассоциативность сложения
Существование нейтрального элемента (нуля) относительно сложения
Существование противоположного элемента
Слайд 6© Веденяпин Е.Н. 2013
Аксиомы сложения и умножения на число
(окончание)
Ассоциативность умножения
на число
Дистрибутивность умножения вектора относительно сложения скаляров
Существование нейтрального элемента (единицы)
относительно умноженияДистрибутивность умножения на скаляр относительно сложения векторов
Слайд 7© Веденяпин Е.Н. 2013
Замечания
Элементы линейного пространства называются векторами.
Если в пространстве
L определено умножение его элементов на вещественные числа, то L
называется вещественным линейным пространством.Если в пространстве L определено умножение его элементов на комплексные числа, то L называется комплексным векторным пространством.
Слайд 8© Веденяпин Е.Н. 2013
1.1.3. Свойства линейного пространства
Свойство 1. Единственность нулевого
вектора
Пусть в L имеются два нулевых вектора
и . Тогда так как то, полагая , получаем
и, полагая , получаем
В силу коммутативности сложения , откуда
Слайд 9© Веденяпин Е.Н. 2013
Свойство 2. Единственность противоположного вектора
Предположим, что в
L у вектора имеются два противоположных вектора
и .Тогда
Следовательно,
и
Отсюда
Слайд 10© Веденяпин Е.Н. 2013
Свойство 3.
Доказательство
Прибавляя к левой и правой
частям равенства выражение , получим
Слайд 11© Веденяпин Е.Н. 2013
Свойство 4.
Доказательство
Прибавляя к левой и правой
частям равенства выражение , получим
Слайд 13© Веденяпин Е.Н. 2013
1.1.4. Примеры линейных пространств
Пример 1. Множество всех
вещественных чисел с обычными операциями сложения и умножения
Данное множество является
линейным пространством, если числовой множитель является элементом множества действительных чисел.Если числовой множитель есть элемент множества комплексных чисел, то данное множество не образует вещественного пространства, так как произведение действительного числа на комплексное число в общем случае есть комплексное число.
Слайд 14© Веденяпин Е.Н. 2013
Пример 2. Множество всех рациональных чисел
Множество
всех рациональных чисел образует линейное пространство, если числовой множитель есть
рациональное число.Если числовой множитель является вещественным или комплексным числом, то это множество векторного пространства не образует.
Слайд 15© Веденяпин Е.Н. 2013
Пример 3
Рассмотрим множество элементов, каждый из
которых является упорядоченной последовательностью из действительных чисел.
Элементы этого множества называются
векторами и обозначаютсяСлайд 16© Веденяпин Е.Н. 2013
Пример 3
(окончание)
Операции сложения векторов и умножения
вектора на число вводятся так:
ВЫВОД. Введенные операции удовлетворяют всем аксиомам
линейного пространства (п. 3.1.1.). Следовательно, это множество является линейным пространством, Rn. Очевидно, что нулевой вектор из Rn имеет вид
Слайд 17© Веденяпин Е.Н. 2013
Пример 4. Множество многочленов
Множество всех многочленов
степени, не превосходящей n, с обычными для многочленов операциями сложения
и умножения на число является линейным пространством. В этом пространстве вектор x имеет вид:где а0, а1, …, an – произвольные числа, х – переменная.
Слайд 18© Веденяпин Е.Н. 2013
1.1.5. Линейное подпространство
Пусть множество R образует некоторое
линейного пространство.
Тогда всякое подмножество R1 множества R, элементы которого также
образуют векторное пространство с теми же самыми операциями сложения и умножения на число, что и в R, называется подпространством векторного пространства R. Теорема. Для того чтобы подмножество R1 множества R было подпространством линейного пространства, необходимо и достаточно, чтобы выполнялись условия
Слайд 19© Веденяпин Е.Н. 2013
Проверка выполнимости аксиом линейного пространства
Необходимость следует из
того, что эти условия должны выполняться для любого векторного пространства.
Для
доказательства достаточности надо показать, что выполняются все восемь аксиом линейного пространства (п. 3.1.2).Справедливость аксиом 1, 2, 4 - 8 очевидна.
Слайд 20© Веденяпин Е.Н. 2013
Проверка выполнимости 3 аксиомы линейного пространства
Докажем, что
аксиома 3 (существование нулевого элемента) выполняется.
По условию
Пусть =0. Тогда
Поскольку
следовательно, аксиома 3 выполняется.Слайд 211.2. Линейная независимость векторов
1.2.1. Определение линейной зависимости
Пусть L – линейное
пространство. Векторы
называются линейно зависимыми, если существуют такие числа 1, 2, …, n, не равные одновременно нулю, что линейная комбинация этих векторов равна нулюВекторы, не являющиеся линейно зависимыми, называются линейно независимыми.
Векторы называются линейно независимыми, если равенство
выполняется, тогда и только тогда, когда 1=0, 2=0, …, n=0.
© Веденяпин Е.Н. 2013
Слайд 22© Веденяпин Е.Н. 2013
1.2.2. Линейные комбинации векторов
Пусть векторы
линейно зависимы, то есть пусть в
соотношениихотя бы один из коэффициентов 1, 2, …, n, например, 1 отличен от нуля.
Тогда
Откуда
Положим
Слайд 23© Веденяпин Е.Н. 2013
Определение линейной комбинации векторов
Получаем выражение одного вектора
через другие векторы
Если вектор выражается через векторы
в видето говорят, что есть линейная комбинация векторов
Слайд 24© Веденяпин Е.Н. 2013
1.2.3. Линейная комбинация и линейная зависимость векторов
Если
векторы линейно зависимы, то хотя бы один из них является
линейной комбинацией остальных.Верно и обратное утверждение: векторы, один из которых есть линейная комбинация остальных, линейно зависимы
Слайд 25© Веденяпин Е.Н. 2013
Примеры линейной зависимости векторов
Пример 1. На прямой
любые два вектора пропорциональны, то есть линейно зависимы.
Пример 2.
На плоскости найдутся два линейно независимых вектора, но всякие три вектора линейно зависимы. Пример 3. Если L – совокупность векторов трехмерного пространства, то найдутся три линейно независимых вектора в R, но всякие четыре вектора линейно зависимы.
ВЫВОД. Видно, что максимальное число линейно независимых векторов на прямой, плоскости, в трехмерном пространстве совпадает с тем, что в аналитической геометрии принято называть размерностью прямой, плоскости, пространства.
Слайд 26© Веденяпин Е.Н. 2013
1.2.4. Размерность линейного пространства
Линейное пространство L называется
n-мерным, если в нем существует n линейно независимых векторов, но
больше чем n линейно независимых векторов оно не содержит.Линейное пространство размерности n обозначается Ln.
Если в пространстве L можно найти любое число линейно независимых векторов, то L называется бесконечномерным.
Слайд 271.3. Базис линейного пространства
1.3.1. Определение базиса линейного пространства
Совокупность любых n
линейно независимых векторов пространства Ln называется его базисом.
Замечание. Согласно
определению n-мерного векторного пространства Ln в нем существует n линейно независимых векторов, то есть существует базис.© Веденяпин Е.Н. 2013
Слайд 28© Веденяпин Е.Н. 2013
1.3.2. Теорема о представлении вектора
Каждый вектор
линейного пространства можно представить, и притом единственным образом, как
линейную комбинацию векторов базиса.Слайд 29© Веденяпин Е.Н. 2013
1.3.3. Координаты вектора
Пусть в n-мерном линейном
пространстве Ln задан базис
Используя выражение
можно установить взаимно однозначное соответствие между
векторами этого пространства и упорядоченными последовательностями из n чисел х1, х2, …, хn.Числа х1, х2, …, хn называются координатами вектора в базисе
Обозначения:
Слайд 30© Веденяпин Е.Н. 2013
Равенство векторов
Из приведенной теоремы следует, что два
вектора
равны тогда и только тогда, когда их координаты в базисе
равны,
то есть когдаСлайд 31© Веденяпин Е.Н. 2013
1.3.4. Операции над векторами в координатной форме
Сложение векторов
Пусть в пространстве Ln задан базис
Тогда любые векторы х
и у из Ln можно единственным образом представить в видеНа основании аксиом сложения векторов получаем
Слайд 32© Веденяпин Е.Н. 2013
Умножение вектора на число
Рассмотрим умножение вектора х
на число .
Пусть в пространстве Ln задан базис
Тогда любой вектор
х из Ln можно единственным образом представить в видеНа основании аксиом умножения вектора на число получаем
Слайд 33Если векторы пространства Ln заданы своими координатами относительно некоторого базиса
, то при
сложении векторов их координаты складываютсяСледовательно, если вектор пространства Ln задан своими координатами относительно некоторого базиса , то при умножении вектора на число его координаты умножаются на это число
© Веденяпин Е.Н. 2013
Выводы
Слайд 34© Веденяпин Е.Н. 2013
1.3.5. Линейные комбинации векторов в координатной форме
Пусть дана линейная комбинация векторов
где
Слайд 35© Веденяпин Е.Н. 2013
Линейные комбинации векторов в координатной форме (окончание)
Тогда
ВЫВОД.
Координаты линейной комбинации векторов являются линейными комбинациями соответствующих координат векторов.
Слайд 36© Веденяпин Е.Н. 2013
1.3.6. Координаты нулевого вектора
У нулевого вектора все
координаты равны нулю.
Доказательство
Так как базисные вектора линейно независимы, то
Слайд 37© Веденяпин Е.Н. 2013
1.3.7. Координаты противоположного вектора
Вектор, противоположный вектору
равен
Доказательство
Слайд 381.4. Примеры базисов линейных пространств
1.4.1. Трехмерное пространство
Для случая трехмерного пространства
L3 определение координат вектора совпадает с имеющимся в аналитической геометрии
определением координат вектора в некоторой системе координат© Веденяпин Е.Н. 2013
Слайд 39© Веденяпин Е.Н. 2013
1.4.2. n-мерное пространство
Пусть имеется Ln – пространство,
векторами которого являются упорядоченные системы
из n чисел.
Очевидно, что n векторов
образуют
базис пространства Ln.Слайд 40© Веденяпин Е.Н. 2013
Определение координат вектора
Найдем координаты вектора х в
данном базисе
ВЫВОД. Числа х1, х2, …, хn можно рассматривать как
координаты векторав базисе
пространства Ln.
Слайд 41© Веденяпин Е.Н. 2013
1.4.3. Пространство многочленов степени n-1
Рассмотрим пространство Ln
многочленов степени не выше n-1.
Базисом является совокупность n векторов
Слайд 42© Веденяпин Е.Н. 2013
Представление многочлена в выбранном базисе
Тогда координатами многочлена
в этом базисе являются его коэффициенты
Слайд 43 2. Преобразование координат при замене базиса
Рассматриваемые вопросы:
2.1. Замена базиса
в трехмерном пространстве
2.2. Пример замены базиса в трехмерном пространстве
2.3. Замена
базиса в n-мерном пространстве2.4. Изоморфизм линейных пространств
© Веденяпин Е.Н. 2013
Слайд 442.1. Замена базиса в трехмерном пространстве
2.1.1. Изменение базиса для пространственной
системы координат
Пусть имеется базис
Рассмотрим другой базис
© Веденяпин Е.Н. 2013
Слайд 45© Веденяпин Е.Н. 2013
Матрица перехода
Базисные вектора нового базиса в старом
базисе
Матрица перехода от старого базиса к новому
ВЫВОД. Столбцы матрицы перехода
образуются из коэффициентов разложения новых базисных векторов по старом базису.Слайд 46© Веденяпин Е.Н. 2013
Матричная форма записи
Используя матрицу перехода, можно соотношению
между новыми и старыми базисными векторами придать матричную форму
Или
Слайд 47© Веденяпин Е.Н. 2013
Обратный переход
Поскольку базисные вектора линейно независимы, то
определитель матрицы перехода А не равен нулю, то есть матрица
перехода невырожденная.Следовательно, существует обратная матрица А-1.
Матрица перехода от нового базиса к старому
Слайд 48© Веденяпин Е.Н. 2013
2.1.2. Связь между координатами вектора в различных
базисах в пространстве
Компоненты вектора а в старом и новом базисах
Подставляя
выражение новых базисных векторов через старые базисные вектора, получаемСвязь между координатами вектора в старом и новом базисах
Слайд 49© Веденяпин Е.Н. 2013
Преобразование координат вектора при переходе от старого
базиса к новому
Выражение новых координат вектора через старые координаты получаем
аналогично.Результат будет идентичен предыдущему, только матрица перехода будет составлена из компонентов старых базисных векторов в новом базисе.
Слайд 50© Веденяпин Е.Н. 2013
2.1.3. Связь между координатами вектора в различных
базисах на плоскости
Компоненты вектора а в старом и новом базисах
на плоскостиПодставляя выражение новых базисных векторов через старые базисные вектора, получаем
Связь между координатами вектора в старом и новом базисах
Слайд 51© Веденяпин Е.Н. 2013
2.1.4. Изменение системы координат в пространстве
Рассмотрим две
декартовы системы координат: старую (0, е1, е2, е3) и новую
(0’, е’1, е’2, е’3).Пусть М – произвольная точка, координаты которой в этих системах координат будут соответственно равны
Выразим координаты точки в старой системе отсчета через координаты в новой системе отсчета, если известно положение новой системы координат относительно старой.
Положение новой системы координат относительно старой определяется координатами начала координат 0’(x’0, y’0, z’0) и компонентами базисных векторов е’1, е’2, е’3, составляющих матрицу перехода.
Слайд 52© Веденяпин Е.Н. 2013
Закон преобразования координат точки при замене базиса
Радиус-векторы
точки М относительно начал координат 0 и 0’ связаны соотношением
Запишем
это соотношение в видеРазложим каждый член равенства по базису е’1, е’2, е’3. Принимаем, что компоненты векторов 0М и 00’ равны координатам точек М и 0’ соответственно.
Координаты точки 0’ равны
Слайд 53© Веденяпин Е.Н. 2013
Закон преобразования координат точки
(окончание)
Получаем закон преобразования координат
точки при переходе от одной пространственной декартовой системы координат к
другой такой же системе координатСлайд 54© Веденяпин Е.Н. 2013
2.1.5. Изменение системы координат на плоскости
Закон преобразования
координат точки при переходе от одной системы координат на плоскости
к другой системе получаются аналогичноСлайд 55© Веденяпин Е.Н. 2013
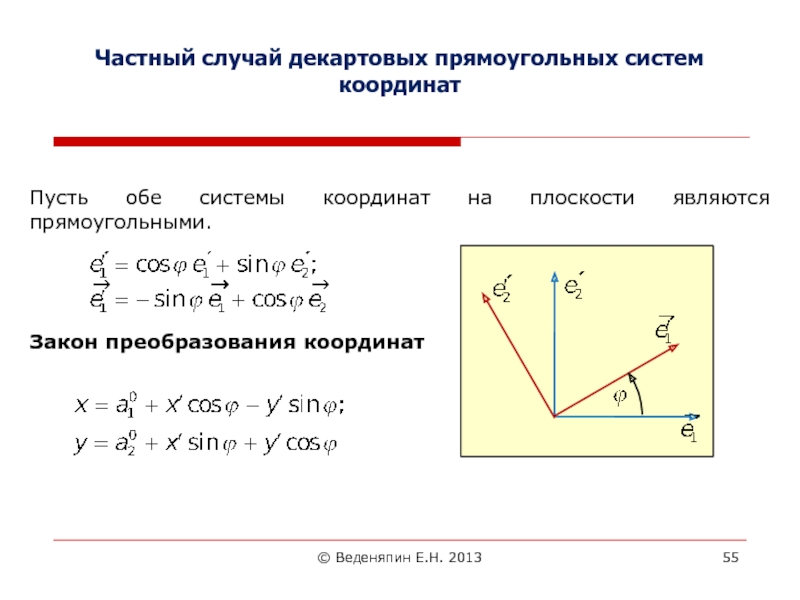
Частный случай декартовых прямоугольных систем координат
Пусть обе
системы координат на плоскости являются прямоугольными.
Закон преобразования координат
Слайд 562.2. Пример замены базиса в трехмерном пространстве
2.2.1. Постановка задачи
В базисе
пространства R3
заданы векторы
© Веденяпин Е.Н. 2013
Слайд 57© Веденяпин Е.Н. 2013
Постановка задачи
(окончание)
Доказать, что векторы а1, а2, а3
образуют базис.
Выразить связь между базисами е1, е2, е3 и а1,
а2, а3.Найти координаты вектора b в базисе а1, а2, а3.
Слайд 58© Веденяпин Е.Н. 2013
2.2.2. Проверка линейной независимости векторов а1, а2,
а3
Векторы а1, а2, а3 образуют базис в пространстве R3, поскольку
они линейно независимы, а их число равно размерности пространства.Доказательство
Составим линейную комбинацию векторов а1, а2, а3 и найдем числа 1, 2, 3, когда линейная комбинация обращается в нуль.
Слайд 59© Веденяпин Е.Н. 2013
Проверка линейной независимости векторов а1, а2, а3
(продолжение)
Найдем
решение системы уравнений относительно 1, 2, 3 с помощью метода
Гаусса.Приведение матрицы коэффициентов системы уравнений к треугольному виду
Определитель
Слайд 60© Веденяпин Е.Н. 2013
Проверка линейной независимости векторов а1, а2, а3
(окончание)
Если
определитель матрицы системы однородных уравнений не равен нулю, то система
имеет только тривиальное решениеВЫВОД. Векторы а1, а2, а3 линейно независимы и, следовательно, образуют базис в пространстве R3.
Слайд 61© Веденяпин Е.Н. 2013
2.2.3. Нахождение вектора b в базисе
а1, а2,
а3
Выразим векторы аi через вектора е1, е2, е3.
Найдем матрицу перехода
АВЫВОД. Найдена матрица перехода от базиса е1, е2, е3 к базису а1, а2, а3.
Слайд 62© Веденяпин Е.Н. 2013
Обратная матрица перехода
Поскольку матрица А невырожденная, то
обратная матрица А-1 существует
Матрица А-1 является матрицей перехода от базиса
а1, а2, а3 к базису е1, е2, е3.Слайд 63© Веденяпин Е.Н. 2013
Координаты вектора b в новом базисе
Координаты вектора
b в базисе а1, а2, а3
Слайд 64© Веденяпин Е.Н. 2013
2.2.4. Нахождение связи между базисами
е1, е2, е3
и а1, а2, а3
Связь между базисом а1, а2, а3 и
е1, е2, е3Связь между базисом е1, е2, е3 и а1, а2, а3
Слайд 662.3. Замена базиса в n-мерном пространстве
2.3.1. Матрица перехода
Пусть в n-мерном
пространстве Rn даны два базиса
И
Разложим каждый вектор второго базиса по
первому базису© Веденяпин Е.Н. 2013
Слайд 67© Веденяпин Е.Н. 2013
Матрица перехода от старого базиса к новому
Столбцы
матрицы перехода образуются из коэффициентов разложения новых базисных векторов по
старом базису.Матричная форма записи
Слайд 68© Веденяпин Е.Н. 2013
Матрица перехода от нового базиса к старому
Матрица
перехода А невырожденная, поскольку базисные вектора линейно независимы.
Следовательно, обратная матрица
А-1 существует.Умножим обе части уравнения на А-1
Отсюда
Слайд 69© Веденяпин Е.Н. 2013
2.3.2. Последовательная замена нескольких базисов
Пусть в линейном
пространстве Rn даны три базиса е, е’, e’’, причем
Получаем
ВЫВОД. При
последовательной замене базисов матрицы перехода перемножаются, причем последующие множители располагаются правее. Слайд 70© Веденяпин Е.Н. 2013
4.3.3. Матрица перехода к произвольному базису
Пусть
задан базис е.
Любая невырожденная матрица А порядка n (det
A≠0) является матрицей перехода от базиса е к некоторому базису е’.Действительно, при det A≠0 столбцы матрицы А линейно независимы и являются координатными столбцами n линейно независимых векторов, которые и составляют базис e’.
Слайд 71© Веденяпин Е.Н. 2013
2.3.4. Компоненты вектора в различных базисах
Пусть имеются
два базиса е и е’.
Пусть имеется некоторый вектор b, который
имеет представление в рассматриваемых базисахПодставим выражение для базиса е’ в формулу
Получим
С другой стороны
Слайд 72© Веденяпин Е.Н. 2013
Компоненты вектора в различных базисах
(окончание)
В силу единственности
координатного столбца получаем
Подробнее эта формула может быть представлена в виде
Слайд 734.4. Изоморфизм линейных пространств
2.4.1. Определение изоморфизма
Линейные пространства R и R’
называются изоморфными, если между их векторами можно установить взаимно однозначное
соответствие, такое, что еслии
то
© Веденяпин Е.Н. 2013
Слайд 74© Веденяпин Е.Н. 2013
2.4.2. Следствие из определения изоморфизма
Из определения изоморфизма
следует, что если
а
то равенство
равносильно равенству
ВЫВОД. Линейно независимым векторам из пространства
R соответствуют линейно независимые векторы из R’.Верно и обратное.
Слайд 75© Веденяпин Е.Н. 2013
2.4.3. Изоморфизм пространств одинаковой размерности
Все линейные
пространства, имеющие одну и ту размерность n, изоморфны между собой.
Пространства
различной размерности не могут быть между собой изоморфны.Действительно, пусть пространства R и R’ изоморфны.
Тогда максимальное количество линейно независимых векторов в R и R’ одно и то же.
Это означает, что оба пространства имеют одинаковую размерность.
Слайд 76 3. Линейные подпространства
Рассматриваемые вопросы:
3.1. Линейные подпространства
3.2. Сумма и пересечение
линейных подпространств
3.3. Свойства суммы и пересечения линейных подпространств
3.4. Линейная оболочка
3.5.
Свойства линейной оболочки© Веденяпин Е.Н. 2013
Слайд 773.1. Линейные подпространства
3.1.1. Определение линейного подпространства
Пусть имеется некоторое линейное пространство
R. Выберем из этого пространства некоторую совокупность векторов и обозначим
ее V.Пусть для любых векторов х и у (хV, уV) и любого числа выполняются условия
Тогда множество векторов V называется линейным подпространством пространства R.
© Веденяпин Е.Н. 2013
Слайд 78© Веденяпин Е.Н. 2013
3.1.2. Примеры линейных подпространств
Пример 1
Каждое пространство R
обладает двумя подпространствами:
нулевым подпространством О
самим пространством R
Нулевое подпространство О
и само пространство R называются тривиальными подпространствами.Слайд 79© Веденяпин Е.Н. 2013
Пример 2
Линейное пространство R1 векторов на прямой,
проходящих через начало координат, имеет два тривиальных подпространства
Слайд 80© Веденяпин Е.Н. 2013
Пример 3
Линейное пространство R2 векторов на плоскости
имеет, кроме двух тривиальных подпространства, бесконечное множество подпространств V’1, V’’1,
V’’’1, ... .Каждое из этих подпространств состоит из векторов, лежащих на прямой, проходящей через начало координат.
Слайд 81© Веденяпин Е.Н. 2013
Пример 4
В геометрическом пространстве R3 векторов пространства
каждая прямая и каждая плоскость, проходящие через начало координат, являются
линейными подпространствами геометрического пространства R3.Слайд 823.2. Сумма и пересечение линейных подпространств
3.2.1. Сумма линейных подпространств
Суммой V’+V’’
линейных подпространств линейного пространства R называется совокупность всех векторов аR,
которые можно представить в виде (разложить)Если для каждого вектора а данное разложение является единственным, то сумма линейных подпространств V’+V’’ называется прямой суммой.
Обозначение:
© Веденяпин Е.Н. 2013
Слайд 83© Веденяпин Е.Н. 2013
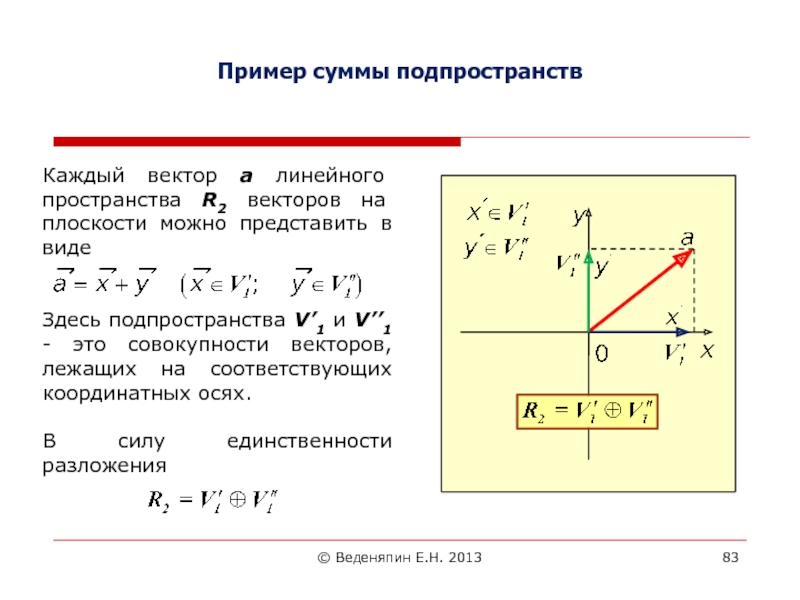
Пример суммы подпространств
Каждый вектор а линейного пространства
R2 векторов на плоскости можно представить в виде
Здесь подпространства V’1
и V’’1 - это совокупности векторов, лежащих на соответствующих координатных осях. В силу единственности разложения
Слайд 84© Веденяпин Е.Н. 2013
3.2.2. Пересечение линейных подпространств
Пересечением V’V’’ линейных подпространств
V’ и V’’ линейного пространства R называется совокупность всех векторов
аR, которые принадлежат одновременно подпространствам V’ и V’’ .Слайд 85© Веденяпин Е.Н. 2013
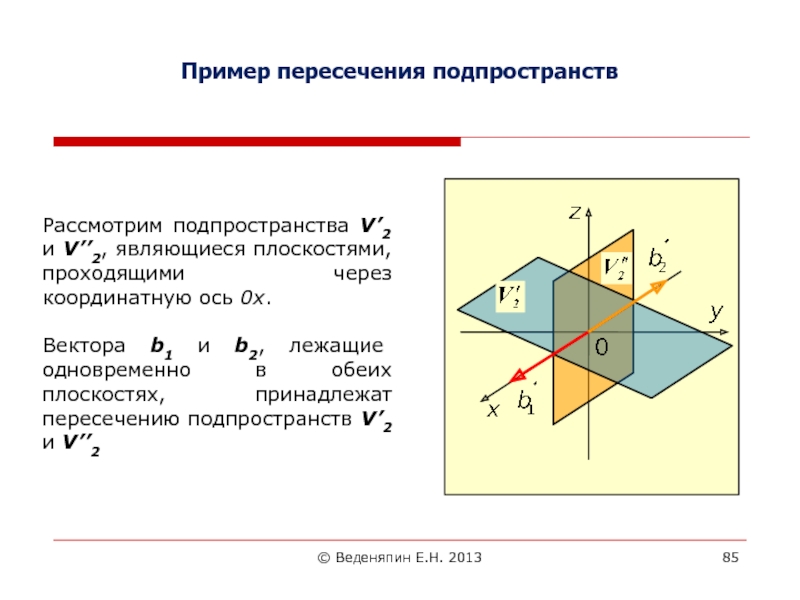
Пример пересечения подпространств
Рассмотрим подпространства V’2 и V’’2,
являющиеся плоскостями, проходящими через координатную ось 0х.
Вектора b1 и b2,
лежащие одновременно в обеих плоскостях, принадлежат пересечению подпространств V’2 и V’’2 Слайд 863.3. Свойства суммы и пересечения линейных подпространств
3.3.1. Первое свойство суммы
и пересечения линейных подпространств
Сумма и пересечение линейных подпространств в свою
очередь являются линейными подпространствами.© Веденяпин Е.Н. 2013
Слайд 87© Веденяпин Е.Н. 2013
3.3.2. Второе свойство суммы и пересечения линейных
подпространств
Размерность суммы линейных подпространств равна сумме размерностей этих подпространств минус
размерность их пересечения.Слайд 883.4. Линейная оболочка
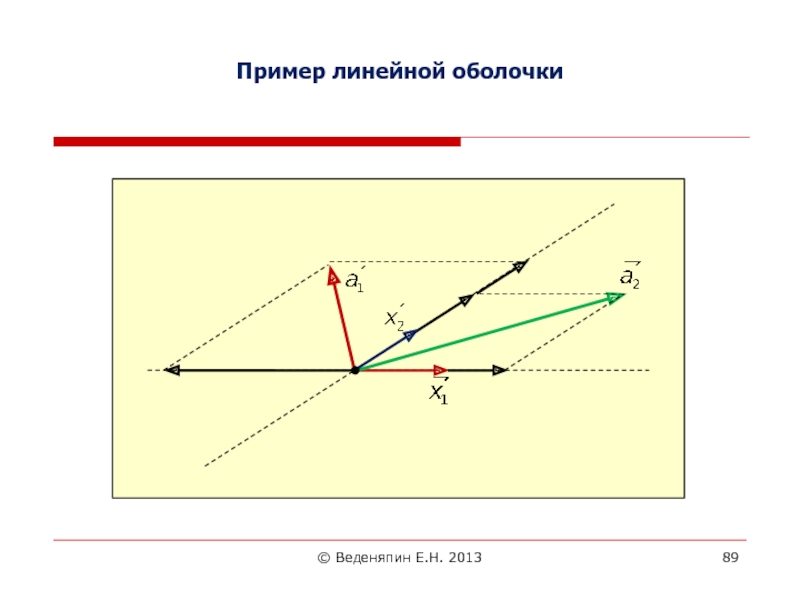
3.4.1. Определение линейной оболочки
Линейной оболочкой L(x1, x2) двух
векторов x1 и x2, принадлежащих линейному пространству R, называется совокупность
всех линейных комбинаций этих векторовЗдесь и - произвольные действительные числа.
Замечание. Линейная оболочка состоит из бесчисленного множества векторов а, которые могут быть представлены в виде линейной комбинации векторов x1 и x2.
© Веденяпин Е.Н. 2013
Слайд 90 4. Евклидово пространство
Рассматриваемые вопросы:
4.1. Евклидово пространство
4.2. Длина вектора и
угол между векторами
4.3. Ортонормированная система векторов
4.4. Процесс ортогонализации векторов
4.5. Построение
ортонормированного базиса© Веденяпин Е.Н. 2013
Слайд 914.1. Евклидово пространство
4.1.1. Определение евклидова пространства
n – мерное векторное пространство
Еn называется евклидовым, если каждой паре векторов x и y
из Еn поставлено в соответствие вещественное число (x, y), называемое скалярным произведением.© Веденяпин Е.Н. 2013
Слайд 93© Веденяпин Е.Н. 2013
Аксиомы скалярного произведения
Скалярное произведение удовлетворяет следующим аксиомам:
Аксиома
линейности по первому аргументу
Аксиома коммутативности
Аксиома положительной определенности
Слайд 94© Веденяпин Е.Н. 2013
Следствие из аксиом скалярного произведения
Из аксиомы линейности
по первому аргументу и аксиомы коммутативности следует свойство линейности скалярного
произведения по второму аргументуСлайд 95© Веденяпин Е.Н. 2013
4.1.2. Первый пример евклидового линейного подпространства
Вектором пространства
En является любая упорядоченная система n действительных чисел
Сложение векторов и
умножение их на число определены ранее.Скалярное произведение векторов
определим формулой
Видно, что аксиомы 1 – 3 действительно выполняются.
Слайд 96© Веденяпин Е.Н. 2013
4.1.3. Второй пример евклидового линейного подпространства
Определим вектор
xEn как упорядоченную совокупность n действительных чисел.
Сложение векторов и
умножение их на число определим так же, как в примере 1.Пусть задана некоторая квадратная матрица А порядка n.
Скалярное произведение векторов x и y определим формулой
Слайд 97© Веденяпин Е.Н. 2013
Пример 2
(продолжение)
Найдем условия, которым должна удовлетворять матрица
А, чтобы определенное данной формулой скалярное произведение удовлетворяло бы аксиомам
1 – 3.Непосредственной проверкой можно убедиться в том, что аксиома 1 выполняется для любой квадратной матрицы А.
Для того, чтобы была выполнена аксиома 2, то есть чтобы выражение (x, y) было симметричным относительно x и y, необходимо и достаточно, чтобы aij=aji, то есть чтобы матрица А, была симметричной.
Слайд 98© Веденяпин Е.Н. 2013
Пример 2
(продолжение)
Для выполнения аксиомы 3 необходимо, чтобы
выражение
было неотрицательно для любых 1, 2, ..., n и обращалось
в нуль лишь если 1=0, 2=0, 3=0, ..., n=0. Слайд 99© Веденяпин Е.Н. 2013
Пример 2
(окончание)
Квадратичная форма (однородный многочлен), определяемая формулой
называется положительно определенной, если она принимает неотрицательные значения при любых
i и обращается в нуль только тогда, когда все i равны нулю. Следовательно, для выполнения аксиомы 3 необходимо, чтобы квадратичная форма
была положительно определенной.
Слайд 100© Веденяпин Е.Н. 2013
Условия, при которых матрица задает скалярное произведение
Всякая
квадратная матрица А порядка n задает скалярное произведение в линейном
пространстве Еn, определяемое формулойпри выполнении следующих условий:
матрица А симметричная;
соответствующая ей квадратичная форма положительно определенная.
Слайд 101© Веденяпин Е.Н. 2013
Частный случай
Если в качестве матрицы А взять
единичную матрицу Е, то есть положить aii=1, а aij=0 (i
j), то скалярное произведение принимает видПолучаем евклидово пространство, определенное в п. 6.1.2.
Слайд 1024.2. Длина вектора и угол между векторами
4.2.1. Норма (длина) вектора
Нормой
(длиной) ||x|| вектора x в пространстве Еn называется корень квадратный
из скалярного произведения вектора х на самого себя© Веденяпин Е.Н. 2013
Слайд 103© Веденяпин Е.Н. 2013
4.2.2. Теорема Пифагора
Векторы x и y ,
скалярное произведение (x, y) которых равно нулю, называются ортогональными.
В любом
евклидовом пространстве Еn верна теорема Пифагора. Теорема. Если векторы x и y ортогональны, то
Слайд 105© Веденяпин Е.Н. 2013
4.2.3. Угол между векторами
Угол между ненулевыми векторами
x и y определяется равенством
Замечание. Если x и y –
ненулевые векторы из Еn, то их ортогональность означает, что угол между ними равенСлайд 106© Веденяпин Е.Н. 2013
Пример
Найти угол между векторами а и b
в четырехмерном пространстве, если
Слайд 107© Веденяпин Е.Н. 2013
4.2.4. Неравенство Коши-Буняковского
В любом евклидовом пространстве Еn
справедливо неравенство Коши-Буняковского
Отсюда следует
Это означает, что косинус угла между векторами
из Еn по модулю, не превосходит единицы.Слайд 108© Веденяпин Е.Н. 2013
Коши и Буняковский
Огюстен Луи
КОШИ
(1789 – 1857)
Виктор Яковлевич
БУНЯКОВСКИЙ
(1804 – 1889)
Слайд 1094.3. Ортонормированная система векторов
4.3.1. Нормированный вектор
Ненулевой вектор x пространства Еn,
называется нормированным, если его норма (длина) равна единице.
© Веденяпин Е.Н.
2013Слайд 110© Веденяпин Е.Н. 2013
4.3.2. Нормирующий множитель
Любой ненулевой вектор можно умножить
на некоторое число так, что в результате получится нормированный вектор.
Доказательство
Действительно,
пусть xEn – ненулевой вектор. Тогда Достаточно взять таким, чтобы
Число называется нормирующим множителем для вектора x.
Слайд 111© Веденяпин Е.Н. 2013
Пример
Найти нормирующий множитель для вектора а, если
Построить
нормированный вектор.
Слайд 112© Веденяпин Е.Н. 2013
4.3.3. Ортонормированная система векторов
Система векторов
в пространства
Еn называется ортогональной, если векторы этой системы попарно ортогональны.
Система векторов
называется ортонормированной, если векторы этой системы попарно ортогональны и имеют норму, равную единице, то есть еслиСлайд 113© Веденяпин Е.Н. 2013
4.3.4. Теорема о линейной независимости ортогональной системы
векторов
Ортогональная система ненулевых векторов пространства Еn линейно независима.
Доказательство
Пусть ненулевые векторы
попарно ортогональны.
Тогда
Слайд 114© Веденяпин Е.Н. 2013
Доказательство
(продолжение)
Покажем, что векторное равенство
выполняется тогда и только
тогда, когда
Умножим обе части равенства
скалярно на а1.
Получим
Слайд 115© Веденяпин Е.Н. 2013
Доказательство
(окончание)
Из условия ортогональности векторов следует, что
Отсюда
Аналогично, умножая
выражение
на а2, получаем
и т.д.
Таким образом, мы доказали, что векторы
линейно
независимы.Слайд 1164.4. Процесс ортогонализации векторов
4.4.1. Суть процесса ортогонализации
Рассмотрим процесс ортогонализации векторов.
Он состоит в том, что из заданных линейно независимых векторов
строятся
k попарно ортогональных векторов © Веденяпин Е.Н. 2013
Слайд 117© Веденяпин Е.Н. 2013
4.4.2. Первый шаг процедуры ортогонализации
Положим
Ищем вектор b2
в виде
Число 21 следует подобрать так, чтобы векторы b1 и
b2 были ортогональны, то естьОтсюда
Слайд 118© Веденяпин Е.Н. 2013
4.4.3. Последующие шаги процедуры ортогонализации
Пусть первые m-1
попарно ортогональные и отличные от нуля векторы
уже построены.
Вектор bm
ищем в видеЗамечание. Вектор bm получаем из вектора аm исправлением его с помощью линейной комбинации уже построенных ранее векторов b1, b2, b3, …, bm-1.
Слайд 119© Веденяпин Е.Н. 2013
Последующие шаги процедуры ортогонализации (продолжение)
Коэффициенты m,1, m,2,
m,3, …, m,m-1 находим из условия ортогональности вектора bm к
векторам b1, b2, b3, …, bm-1.Слайд 120© Веденяпин Е.Н. 2013
Последующие шаги процедуры ортогонализации (продолжение)
Так как векторы
b1, b2, b3, …, bm-1 попарно ортогональны, то из полученных
равенств имеемСлайд 121© Веденяпин Е.Н. 2013
Последующие шаги процедуры ортогонализации (окончание)
Из полученной системы
уравнений находим коэффициенты m,1, m,2, m,3, …, m,m-1
Слайд 122© Веденяпин Е.Н. 2013
4.4.4. Неравенство нулю вектора bm
Докажем теперь, что
построенный вектор bm отличен от нуля.
Вектор bm есть линейная
комбинация векторов b1, b2, b3, …, bm-1. Но вектор bm можно заменить линейной комбинацией вектора аm и векторов b1, b2, b3, …, bm-2 и т.д.
Окончательно получаем, что вектор bm записывается в виде
Отсюда следует, что bm 0.
В противном случае левая часть равенства была бы равна 0, что противоречит линейной независимости векторов (коэффициент при аm равен единице).
Слайд 123© Веденяпин Е.Н. 2013
4.4.5. Заключительные замечания
По векторам b1, b2, b3,
…, bm-1 и аm построен вектор bm.
Аналогично по векторам
b1, b2, b3, …, bm-1, bm и аm+1 можно построить вектор bm+1. Продолжая этот процесс, можно по заданной системе n линейно независимых векторов в Еn построить систему n ненулевых ортогональных векторов.
Слайд 1246.5. Построение ортонормированного базиса
6.5.1. Теорема о существовании ортонормированного базиса
Во всяком
евклидовом пространстве Еn существуют ортонормированные базисы.
© Веденяпин Е.Н. 2013
Слайд 125© Веденяпин Е.Н. 2013
4.5.2. Пример построения ортонормированного базиса
По заданной в
Еn системе линейно независимых векторов
построить ортонормированный базис.
Положим
Слайд 129© Веденяпин Е.Н. 2013
Построение ортонормированного базиса
Нормируем векторы b1, b2, b3.
Получим ортонормированный базис
Слайд 130© Веденяпин Е.Н. 2013
4.5.3. Координатное представление скалярного произведения
Пусть
– произвольный
базис пространства Еn.
Пусть имеются векторы
Скалярное произведение векторов х и у
имеет видСлайд 131© Веденяпин Е.Н. 2013
Скалярное произведение в ортонормированном базисе
Пусть
– ортонормированный базис.
Следовательно,
Тогда
скалярное произведение векторов представляется в виде
Слайд 132© Веденяпин Е.Н. 2013
Обратное утверждение
Если в базисе
скалярное произведение векторов
х и у равно
то этот базис ортонормированный.
Если в некотором базисе
скалярное произведението этот базис ортонормированный.
Слайд 133© Веденяпин Е.Н. 2013
4.5.4. Ортогональная проекция вектора
Пусть
– ортонормированный базис
в Еn и
Умножив обе части последнего равенства скалярно на
аi, получимВидно, что i-я координата вектора в ортонормированном базисе равна скалярному произведению вектора х на единичный вектор аi.
Скалярное произведение (х, аi) называется ортогональной проекцией вектора х на вектор аi.
ВЫВОД. Координаты вектора в ортонормированном базисе – это его проекции на базисные векторы.