Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пересечение многогранных поверхностей
Содержание
- 1. Пересечение многогранных поверхностей
- 2. Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линииПроницание частичное
- 3. В частных случаях эта ломаная может распадаться
- 4. Способ ребер построение вершин ломаной как
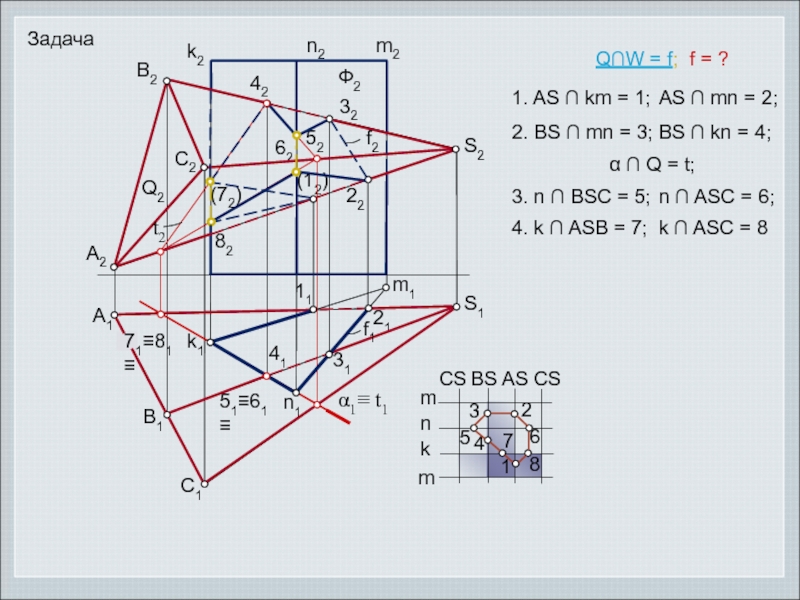
- 5. А1В1С1S1k1m1m2n2k2S2А2B2C241312111nkmCSBSASCSn1m1234(12)2232421. AS ∩ km = 1; AS
- 6. Скачать презентанцию
Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой ломаной линииПроницание частичное
Слайды и текст этой презентации
Слайд 2Две многогранные поверхности в общем случае пересекаются по пространственной замкнутой
ломаной линии
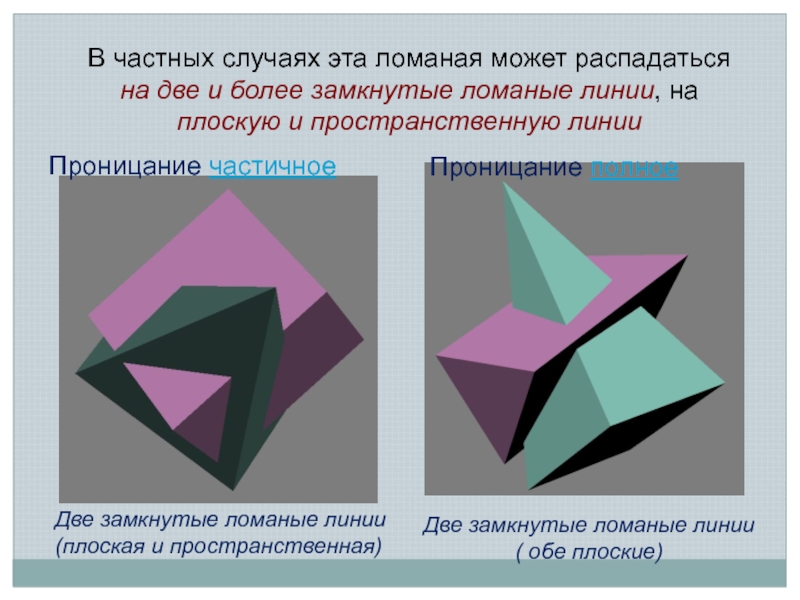
Слайд 3В частных случаях эта ломаная может распадаться на две и
более замкнутые ломаные линии, на плоскую и пространственную линии
Проницание полное
Две
замкнутые ломаные линии (плоская и пространственная)Две замкнутые ломаные линии ( обе плоские)
Проницание частичное
Слайд 4Способ ребер построение вершин ломаной как точек пересечения ребер
первого многогранника с гранями второго и ребер второго с гранями
первого
Способ граней построение сторон ломаной как отрезков прямых попарного пересечения граней данных многогранников
прямыми соединяются проекции только тех точек, которые принадлежат одной грани
Слайд 5А1
В1
С1
S1
k1
m1
m2
n2
k2
S2
А2
B2
C2
41
31
21
11
n
k
m
CS
BS
AS
CS
n1
m
1
2
3
4
(12)
22
32
42
1. AS ∩ km = 1;
AS ∩ mn =
2;
2. BS ∩ mn = 3;
BS ∩ kn =
4;3. n ∩ BSC = 5;
n ∩ ASC = 6;
4. k ∩ ASB = 7;
k ∩ ASC = 8
5161
7181
(72)
82
52
62
5
6
7
8
α1 t1
t2
∩ Q = t;
Q∩W = f; f = ?
f1
f2
Задача
Ф2
Q2
