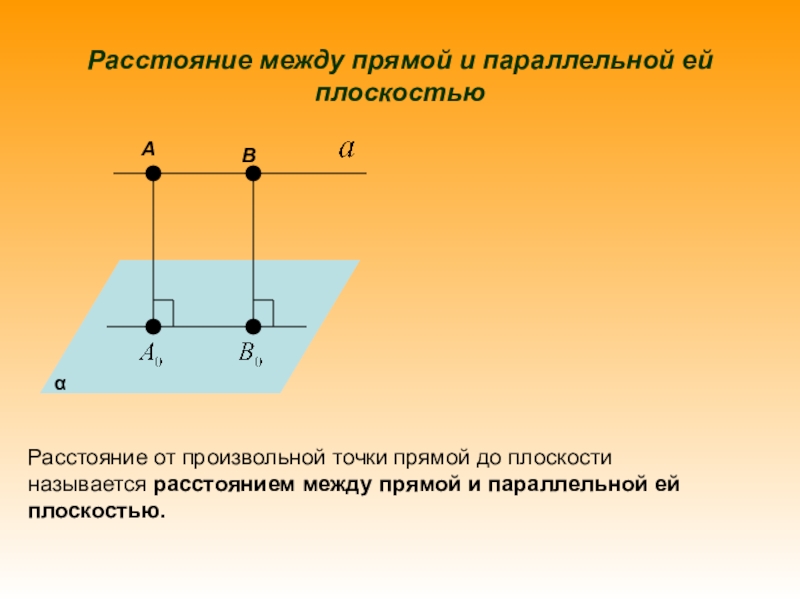
ПРЯМОЙ И ПАРАЛЛЕЛЬНОЙ ЕЙ ПЛОСКОСТЬЮ
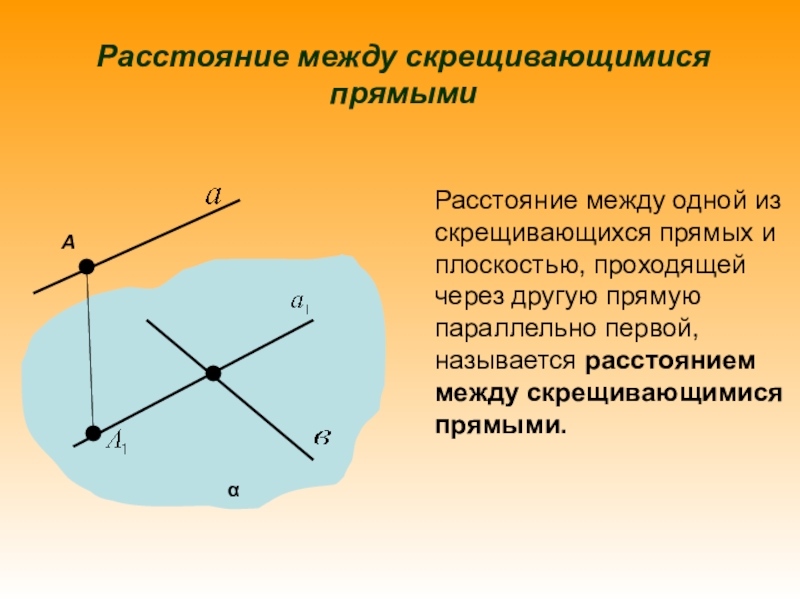
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
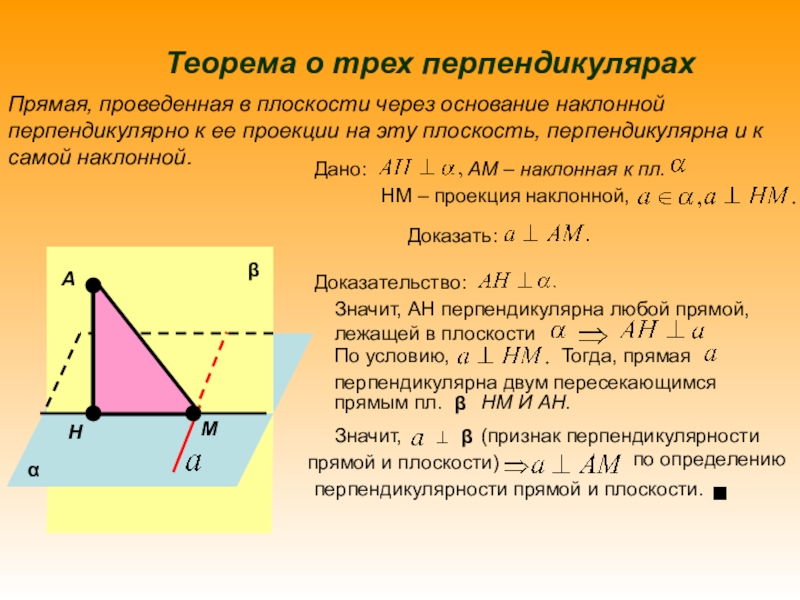
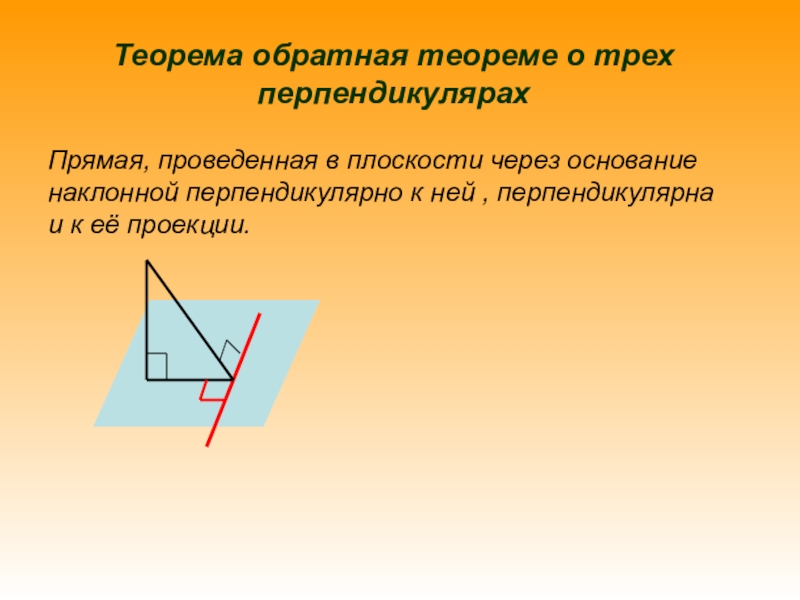
ДОКАЗАТЬ ТЕОРЕМУ О
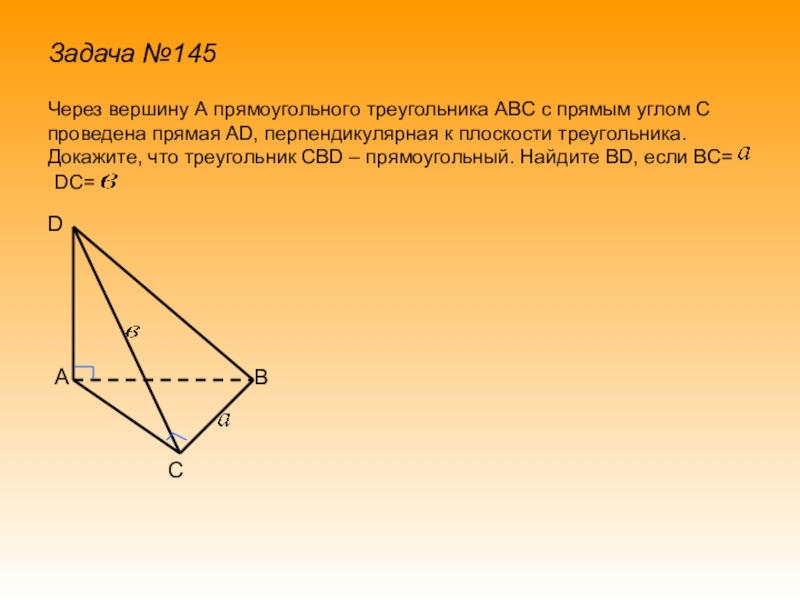
ТРЕХ ПЕРПЕНДИКУЛЯРАХНАУЧИТСЯ ПРИМЕНЯТЬ ТЕОРЕМУ О ТРЕХ ПЕРПЕНДИКУЛЯРАХ ПРИ РЕШЕНИИ ЗАДАЧ























![Блок №3 | [продолжение]
Чтобы сохранить вовлеченность, нам надо чтобы](/img/thumbs/ab172555748dd55bb91846e5ac965ffe-800x.jpg)
