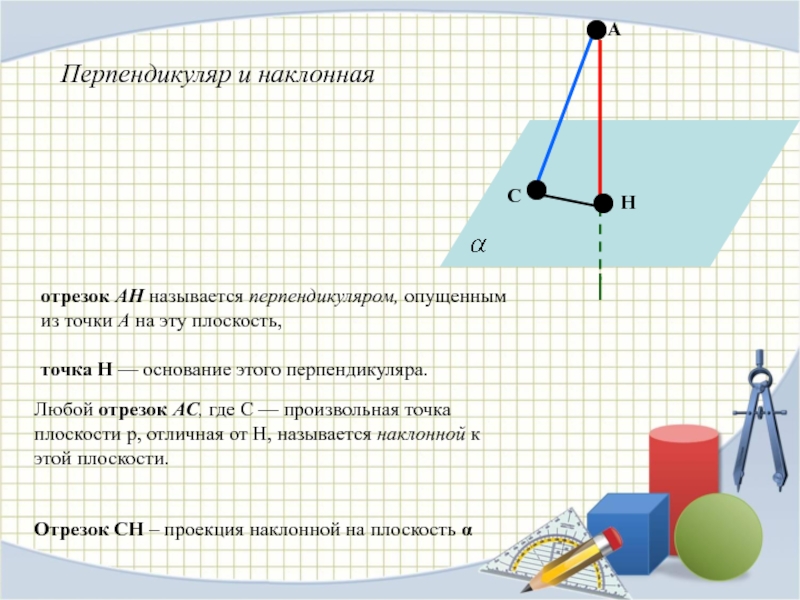
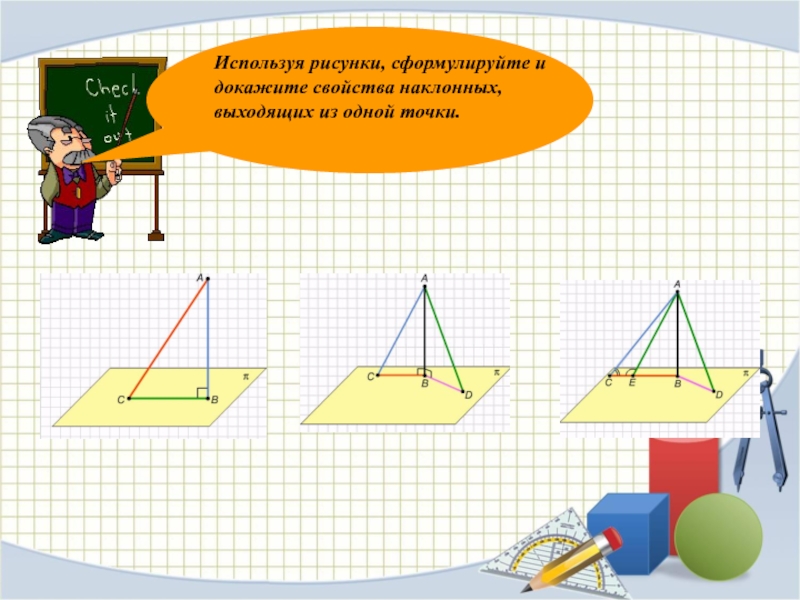
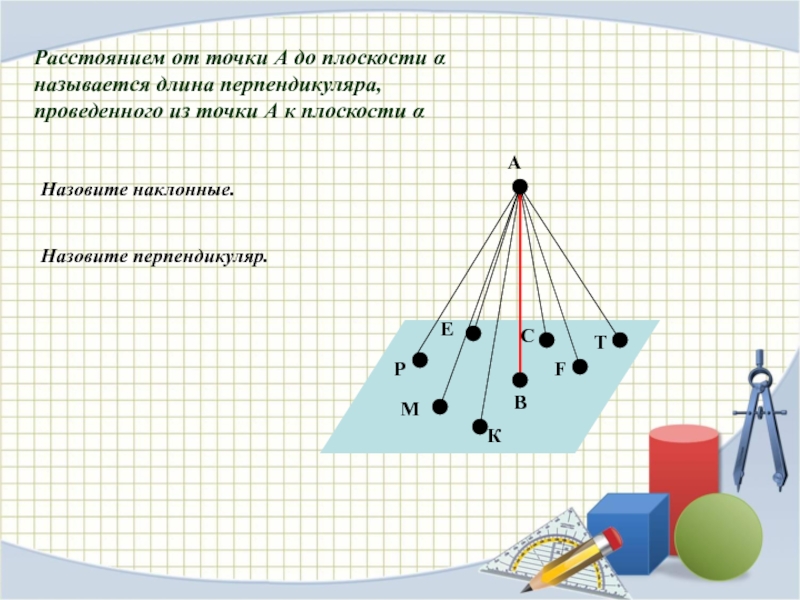
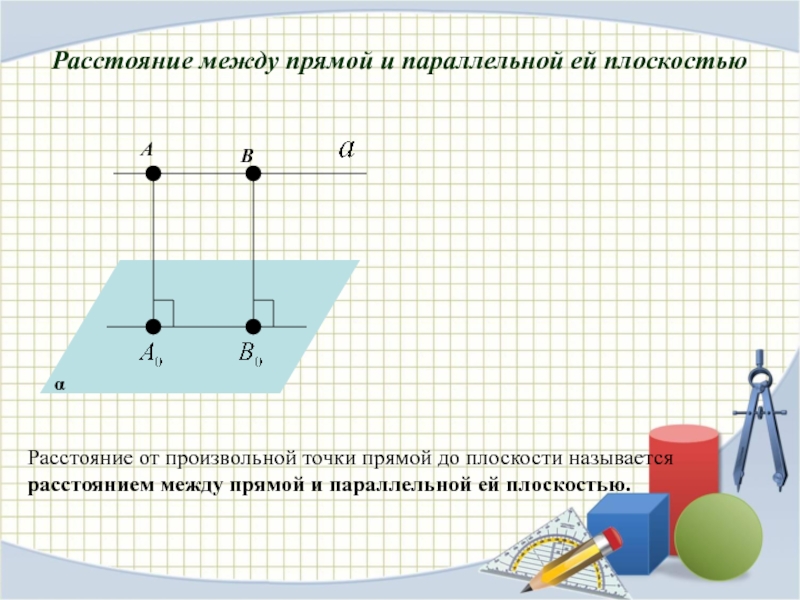
ПЛОСКОСТЯМИ
РАССТОЯНИЕ МЕЖДУ ПРЯМОЙ И ПАРАЛЛЕЛЬНОЙ ЕЙ ПЛОСКОСТЬЮ
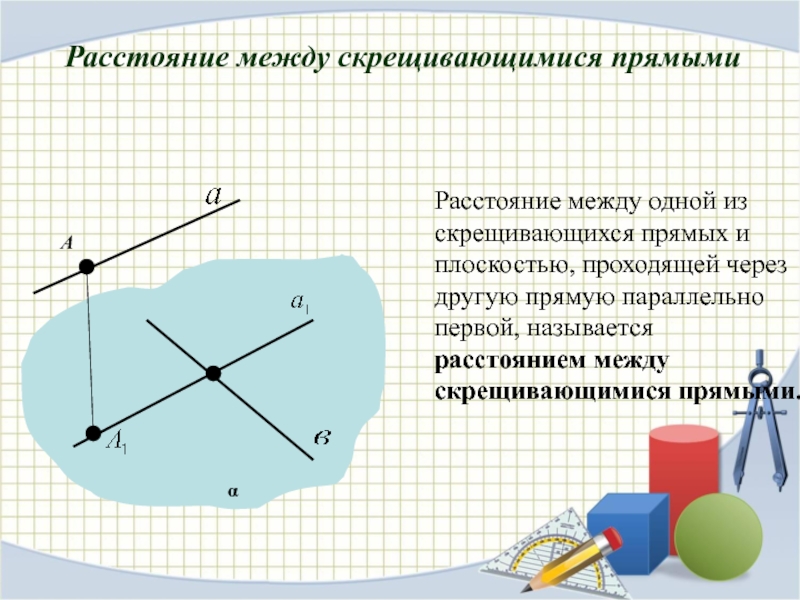
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
ДОКАЗАТЬ
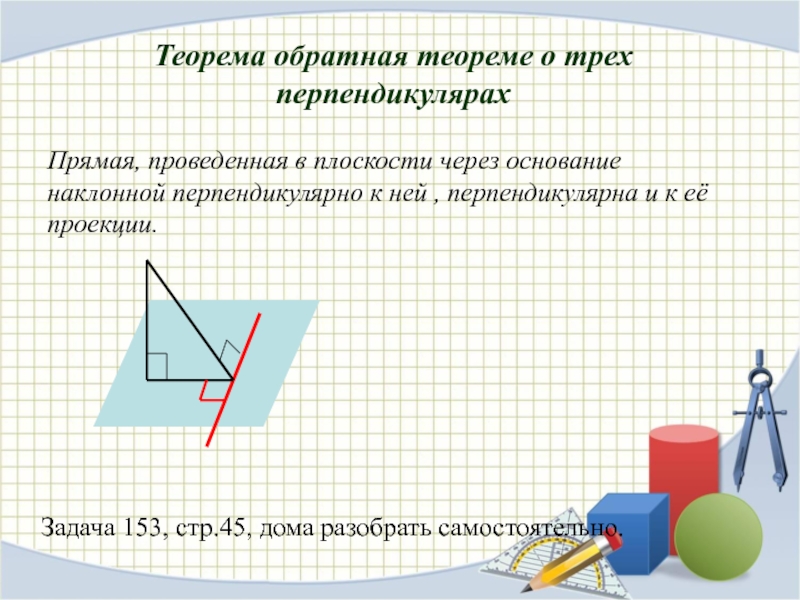
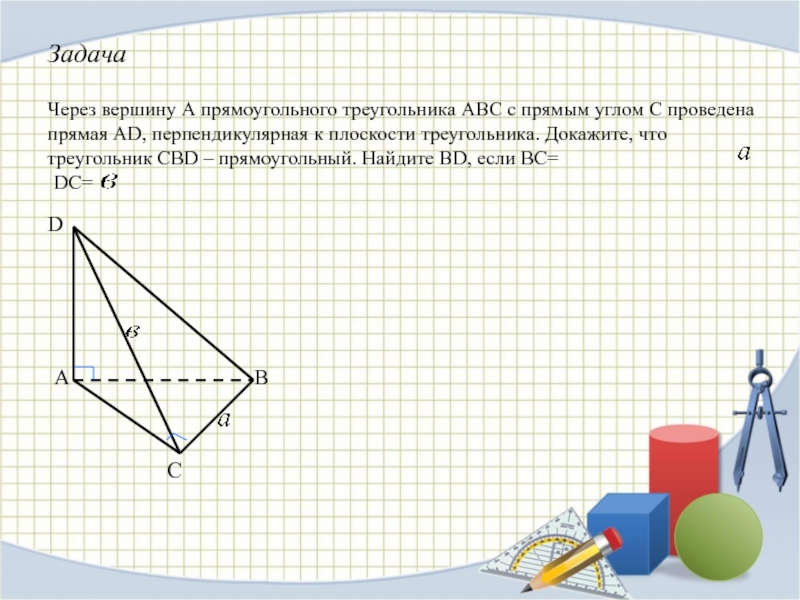
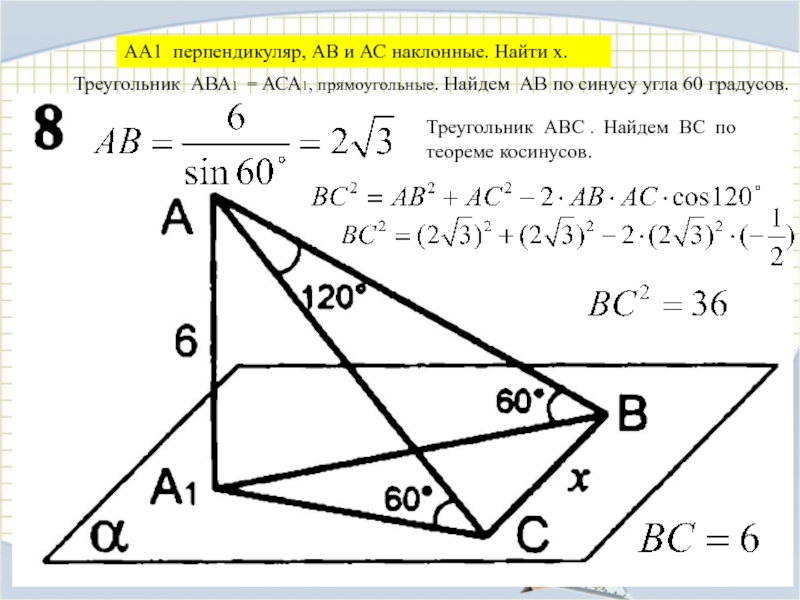
ТЕОРЕМУ О ТРЕХ ПЕРПЕНДИКУЛЯРАХНАУЧИТСЯ ПРИМЕНЯТЬ ТЕОРЕМУ О ТРЕХ ПЕРПЕНДИКУЛЯРАХ ПРИ РЕШЕНИИ ЗАДАЧ