Слайд 1Первообразная
и интеграл
11 класс
Слайд 3Определение
Функция F(х) называется первообразной функции f(х) на промежутке Х, если
На практике промежуток Х обычно не указывают, но подразумевают (область
определения функции).
Например: функция у = х² является первообразной для функции у=2х, т.к. для любого х справедливо
(х²)´ = 2х.
Слайд 4Теорема 1
Если функция f(х) непрерывна при
,
то для f(х) существует первообразная F(х) на Х.
Слайд 5Теорема 2
Если F(x) одна из первообразных функции f(x), на промежутке
Х, то у функции у = f(x) бесконечно
много первообразных, и все они имеют вид
у = F(x)+C.
Слайд 6Таблица первообразных
Зная формулы для нахождения производных, можно составить
таблицу для нахождения первообразных
Слайд 7Правила нахождения первообразных
Первообразная суммы равна сумме первообразных
Если F(x) – первообразная
для f(x), то к·F(x) – есть первообразная для к· f(x).
Если
F(x) – первообразная для f(x), то первообразной для функции у= f(кx+m) служит функция у = 1/к· F(кx+ m)
Слайд 81.Проверь себя.
Соотнеси выражения в правом и левом столбцах
Если f(x)
равно:
1) f(x)=2х+х³
2) f(x)=4х-2
3) f(x)=х³-3х²+х-1
4) f(x)=4х⁵+2х+е
5) f(x)=х⁴+3х²+5
6) f(x)=5cosx-3sin2x
Значит F(x) равно:
F(x)= х²+х⁴⁄4
F(x)=2х²-2х
F(x)=х⁴⁄4-2х³+х²⁄2-х
F(x)=2х⁶⁄3+х²+ех
F(x)=х⁵⁄5+х³+5х
F(x)=5sinx+3/2cosx
Слайд 92. Ответить на вопрос:
какая функция является перообразной для функции
f(x)= 2sinx – cosx?
А)
cosx - 2sinx
Б) 2cosx - sinx
В) -2cosx - sinx
Г) –cosx + 2sinx
Слайд 103. Выберите ответ, при котором предложение будет верно.
Функция F(x) является
первообразной для функции f(x),
если: А) F'(x) = f(x)
Б) F'(x) = - f(x)
В) f'(x) = F(x)
Г) f(x) = F(x)
Слайд 114. Ответить на вопрос:
для какой функции первообразной
является функция F(x)=2x³+6x²+x-9?
А) f(x) = 1/4·x⁴+2x³+x²-9x
Б) f(x) = 2x⁴+6x³+x²-9x
В)
f(x) = 6x²+12x+1
Г) f(x) = x⁴⁄2+2x³+1/2·x²-9x
Слайд 125. Ответить на вопрос: производная какой из функций равна у
= 4х - 3х²?
А) F(x) = 2x³-2x²+C
Б) F(x) = 2x²-1/3·x+C
В)
F(x) = 2x²-x³+C
Г) F(x) = 4x²-x⁴+C
Слайд 13Записать в тетрадь.
Примеры с решениями
Слайд 14Задание №1. Найдите первообразную функции f(x), график которой проходит через
точку А.
а) f(x)=5х+х², А(0;3)
б) f(x)=3х - 5, А(4;10)
Решение.
а) Найдём первообразные
F(x)= 5х²⁄2+х³⁄3+ С, где С – произв.число.
Найдём это С:
т.к. график проходит через точку А(0;3), то
F(0)= 5·0²⁄2+0³⁄3+ С = С и равно 3. С=3
Значит производная, график которой проходит через т. А, имеет вид:
F(x)= 5х²⁄2+х³⁄3+3.
Слайд 15б) f(x)=3х - 5, А(4;10)
Решение.
F(x)= 3х²⁄2-5х+С, где С
– произв. число.
F(4)= 3·4²⁄2-5·4+С=24-20+С=4+С и
4+С=10 => С=6,
тогда
F(x)= 3х²⁄2-5х+6
Ответ: F(x)= 3х²⁄2-5х+6
Слайд 16Выполни самостоятельно
Найдите первообразную функции f(x), график которой проходит через точку
А, если:
1) f(x)=х²-5, А(3;4)
2) f(x)=2х²+3,
А(-2;-5)
3) f(x)=(х-2)², А(0;2)
4) f(x)=cos3x, А(0;1)
Слайд 17Задание №2. Найдите первообразную функции f(x), значение которой при х
= х₀
равно у₀.
а) f(x)=10х⁴+х; х₀=0;
у₀=6
Решение.
F(x)= 10х⁵⁄5 + х²⁄2 + С =
= 2х⁵+ х²⁄2 +С, где С – произв. число.
Найдём С. Т.к. по условию F(x₀)=у₀,
то F(0)=2·0⁵+0²⁄2+С=С и равно у₀= 6.
Значит ответ: F(x)=2х⁵+х²⁄2+6
Слайд 18б) f(x)=2sin3x+4cos(x/2); х₀=π⁄3; у₀=0
Решение.
F(x)=-2·1/3·cos3x+4·2 sin(x/2)+С=
=-2/3·cos3x+8· sin(x/2)+С, где
С- пр. ч.
Найдём С. Т.к. по условию F(x₀)=у₀,
то F(π⁄3)=-2/3·cos
π+8sin(π/6)+С=
=2/3+8·1/2+С=4(2/3)+С и равно 0.
Тогда С = -4(2/3).
Значит F(x)=-2/3·cos3x+8· sin(x/2)-4(2/3)
Слайд 19в) f(x)=4+6х²; х₀=2; у₀
Найдём С: т.к. F(х₀)= у₀ , то
F(2)= 4·2+6·2³⁄3+С= 8+16+С=24+С
и 24+С <0 => С <-24.
Пусть это будет (-25).
Тогда ответ F(x)= 4х+6х³⁄3-25
Слайд 20г) f(x)=2х³+х²+3; х₀=1; у₀>0
Решение.
F(x)= 2х⁴⁄4+х³⁄3+3х+С, где С- пр.ч.
Найдём С.
F(1)= 2·1⁴⁄4+1³⁄3+3·1+С = 3(5/6)+С,
но 3(5/6)+С>0 => С >
- 3(5/6)
Пусть С=-1, тогда
F(x)= 2х⁴⁄4+х³⁄3+3х-1
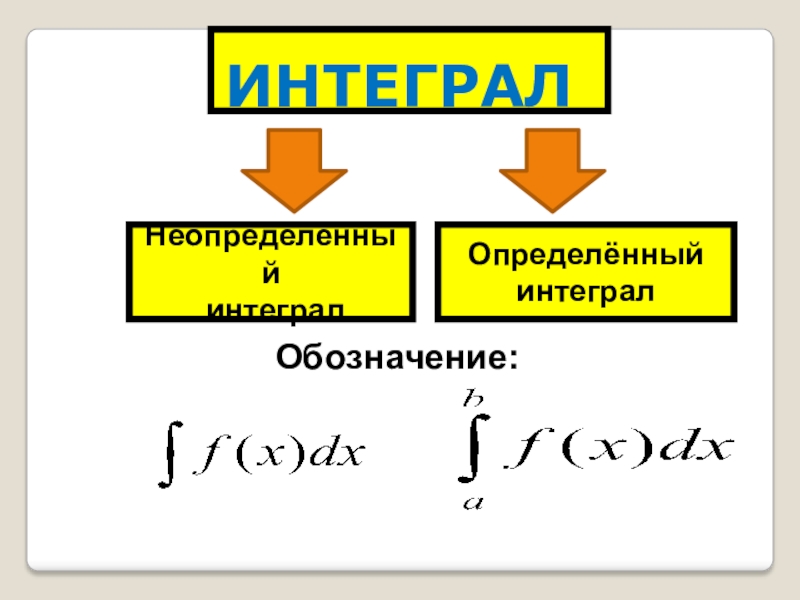
Слайд 22 ИНТЕГРАЛ
Неопределённый
интеграл
Определённый
интеграл
Обозначение:
Слайд 24Определение:
Множество всех первообразных функции f(x) на некотором промежутке называется
неопределенным интегралом от функции f(x) на этом промежутке и обозначается
Слайд 26Определение
Процесс нахождения интеграла называется интегрированием.
Интегрирование является операцией, обратной
дифференцированию
Слайд 27Историческая справка
Интегрирование прослеживается еще в древнем Египте, примерно в 1800
г. до н.э, Московский математический папирус демонстрирует знание
формулы объёма усеченной пирамиды.
Слайд 28Историческая справка
метод исчерпывания Евдокса (примерно 370 до н.э.),
который пытался найти площади и объемы, разрывая их на бесконечное
множество частей, для которых площадь или объем уже были известны.
Первым известным методом для расчета интегралов является
Слайд 29Историческая справка
Этот метод был подхвачен и развит Архимедом,
и использовался для расчета площадей, парабол и приближенного расчета площади
круга.
Слайд 30Историческая справка
Аналогичные методы были разработаны не зависимо в Китае
в 3-м веке н.э. Лю Хуэйем, который использовал их для
нахождения площади круга.
Слайд 31Историческая справка
Этот метод впоследствии использовали Цзу Чунжи и Цзу Гэн
для нахождения объема шара
Слайд 32Историческая справка
Следующий крупный шаг в исследование интегралов был сделан в
Ираке, в XI веке, математиком Ибн ал-Хайсаном
(
известным как Alhazen в Европе), в своей работе «Об измерении параболического тела» он приходит к уравнению четвертой степени.
Решая эту проблему, он проводит вычисления, равносильные вычислению определенного интеграла, чтобы найти объем параболоида. Используя математическую индукцию, он смог обобщить свои результаты для интегралов от многочленов до четвертой степени.
Слайд 33Новая тема.
Всё записать в тетрадь
Слайд 35Определение
Пусть функция y=f(x) определена и интегрируема на отрезке [a,b]
и пусть F(x) – некоторая ее первообразная. Тогда число F(b)–F(a)
называется интегралом от а до b функции f(x) и обозначается
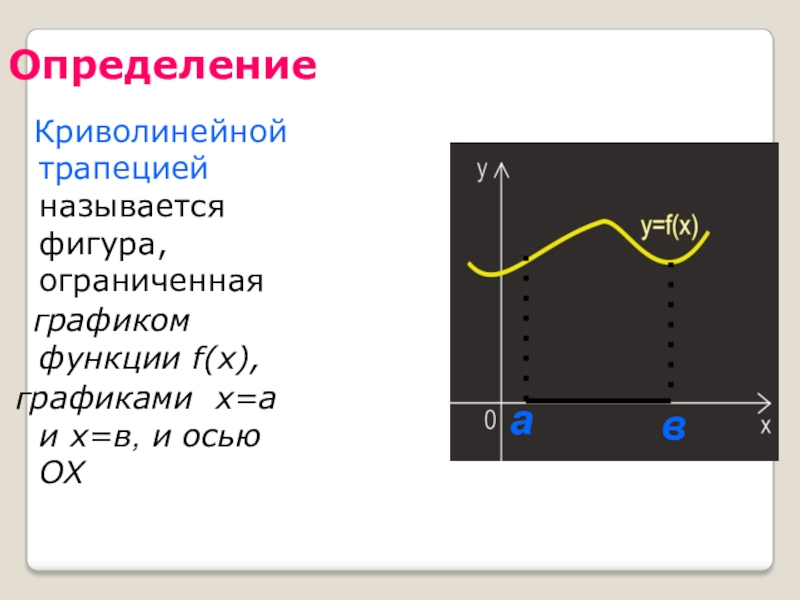
Слайд 36Определение
Криволинейной трапецией называется фигура, ограниченная
графиком функции f(x),
графиками х=а и х=в, и осью ОХ
а
в
Слайд 37Формула Ньютона-Лейбница
Теорема: если функция у = f(x) непрерывна на отрезке
[а;в], то справедлива формула
Опираясь на эту формулу получаются следующие свойства
определенного интеграла
Слайд 38Свойства определенного интеграла
Слайд 39Свойства определенного интеграла
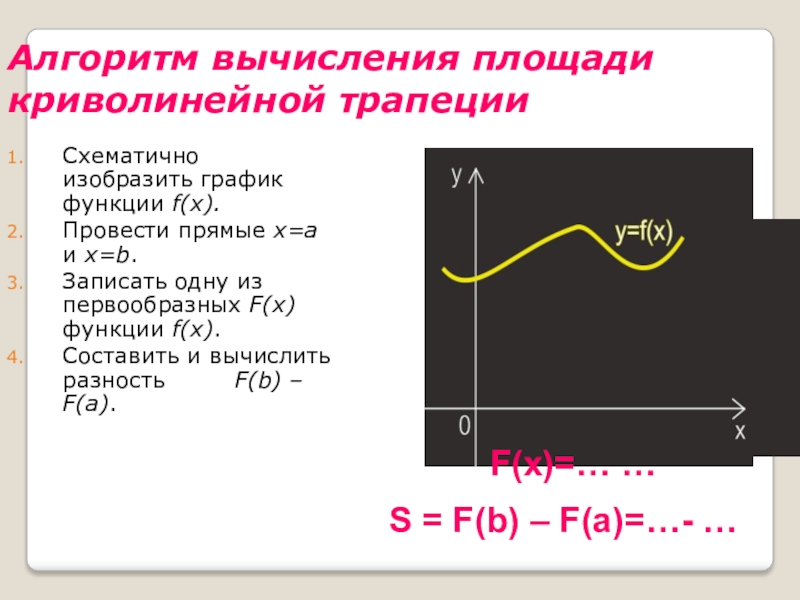
Слайд 40Алгоритм вычисления площади криволинейной трапеции
Схематично изобразить график функции f(x).
Провести прямые
x=a и x=b.
Записать одну из первообразных F(x) функции f(x).
Составить и
вычислить разность F(b) – F(a).
F(x)=… …
S = F(b) – F(a)=…- …
Слайд 41Вычислить площадь фигуры,
ограниченной линиями, используя формулу Ньютона-Лейбница
Вариант 1
f(x) =
2x – 3
y = 0,
x = 3,
x = 5
Вариант
2
f(x) = – 2x – 3
y = 0,
x = – 5,
x = – 3
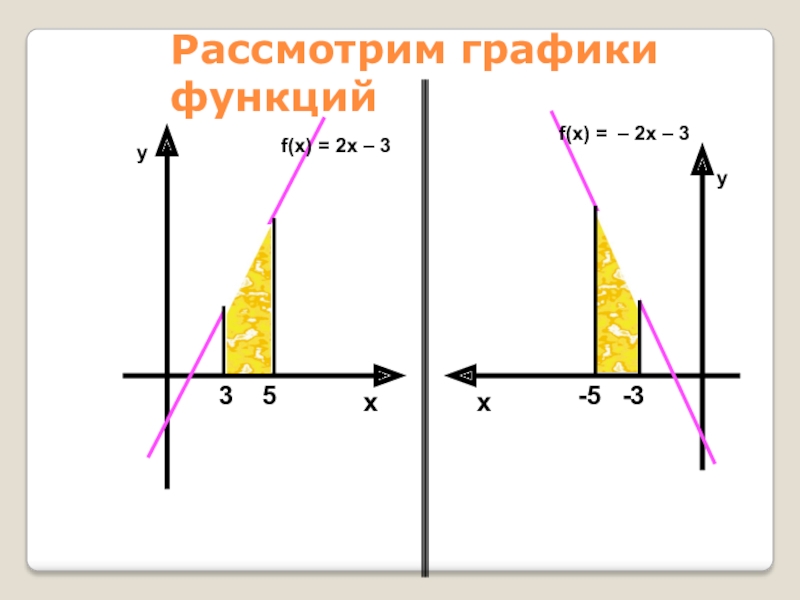
Слайд 42Рассмотрим графики функций
f(x) = 2x – 3
f(x) = – 2x
– 3
у
у
х
х
3
5
-5
-3
Слайд 43Запомним
Геометрический смысл определенного интеграла – это площадь криволинейной трапеции
Физический смысл
определенного интеграла – это…
(Найди и запиши сам!)
Слайд 44Найти площадь фигуры, ограниченной линиями
1) y=–3x²–2, x=1,
x=2, y=–1
2) у= 4x–x², y=0
3) y= x²–2x+3,
x+y=5
4) y=x², y=x
Слайд 45Используемые ресурсы
http://static4.depositphotos.com/1000765/286/i/950/depositphotos_2868805-3d-small---think.jpg
http://awardwinningvideomarketing.com/img/pics/stick_figure_sitting_confused_500_wht.gif
http://nashashcola.ru/wp-content/uploads/2013/08/Velikie_matematiki-Arhimed_Zakon_Arhimeda-2.jpg
http://cs7010.vk.me/c540102/v540102299/2a4b7/gxoZstcDO4w.jpg
http://cdn2-b.examiner.com/sites/default/files/styles/image_content_width/hash/07/06/07060c3d798d1877de2dffd5882c8dfb.jpg?itok=Bf1WO6a0
http://1.bp.blogspot.com/_UAzEooLfuI8/RvU4t7vWjkI/AAAAAAAAA8U/4Yk8JThK_0g/s320/suntzu_portrait-rev.jpg
![Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и пусть F(x) – некоторая ее первообразная.](/img/tmb/7/620040/f3bebf66b0980a000d4b4748999207db-800x.jpg "Первообразная
и интеграл
11 класс Определение Пусть функция y=f(x) определена и интегрируема на отрезке [a,b] и")
![Формула Ньютона-ЛейбницаТеорема: если функция у = f(x) непрерывна на отрезке [а;в], то справедлива формулаОпираясь на эту формулу](/img/tmb/7/620040/4c270f0a4baf8e635a2ead34caa8308d-800x.jpg "Первообразная
и интеграл
11 класс Формула Ньютона-ЛейбницаТеорема: если функция у = f(x) непрерывна на отрезке [а;в],")
