Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пирамида
Содержание
- 1. Пирамида
- 2. исторические сведения о пирамиде
- 3. ПИРАМИДАМногогранник, составленный из n-угольника АB…E и n-треугольников,
- 4. Многоугольник АВ…Е называется основанием, а треугольники-
- 5. Правильная пирамидаПирамида называется правильной, если её основание
- 6. Все боковые рёбра правильной пирамиды равны, а
- 7. ТЕОРЕМА: площадь боковой поверхности правильной пирамиды равна
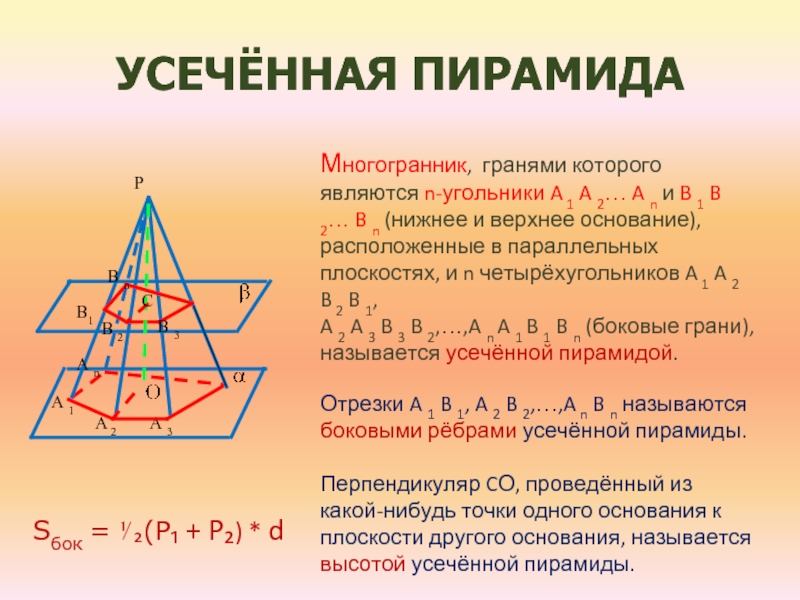
- 8. Усечённая пирамидаМногогранник, гранями которого являются n-угольники A
- 9. Усечённая пирамидаБоковые грани усечённой пирамиды-трапеции. Усечённая пирамида
- 10. Слайд 10
- 11. Благодарю за внимание!
- 12. Скачать презентанцию
исторические сведения о пирамиде Египетские пирамиды – одно из семи чудес света. Что же такое пирамиды? Усыпальницы египетских фараонов. Крупнейшие из них — пирамиды Хеопса, Хефрена и
Слайды и текст этой презентации
Слайд 2
исторические сведения о пирамиде
Египетские пирамиды – одно из семи
чудес света. Что же такое пирамиды?
Крупнейшие из них — пирамиды Хеопса, Хефрена и Микерина в Эль-Гизе в древности считались одним из Семи чудес света. Самая большая из трех — пирамида Хеопса (зодчий Хемиун, 27 в. до н. э.). Ее высота была изначально 147 м, а длина стороны основания — 232 м.
Слайд 3ПИРАМИДА
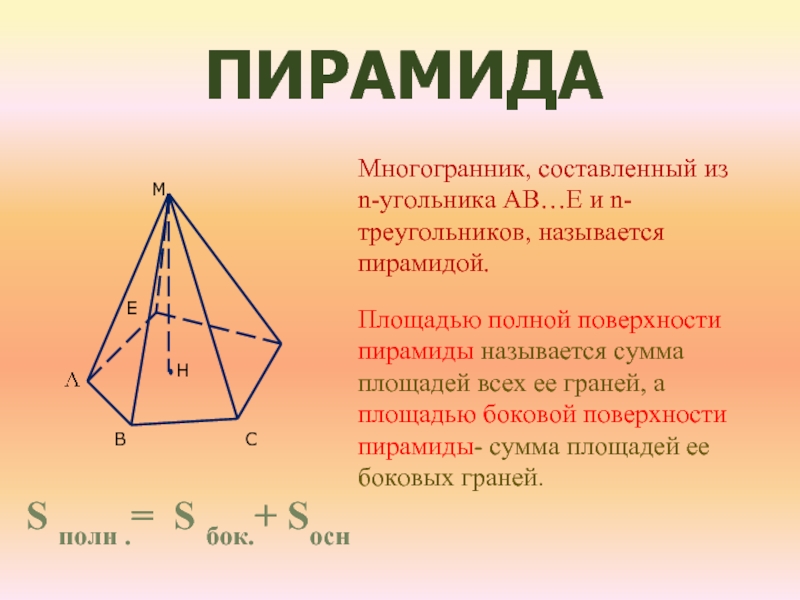
Многогранник, составленный из n-угольника АB…E и n-треугольников, называется пирамидой.
Площадью полной
поверхности пирамиды называется сумма площадей всех ее граней, а площадью
боковой поверхности пирамиды- сумма площадей ее боковых граней.S полн .= S бок.+ Sосн
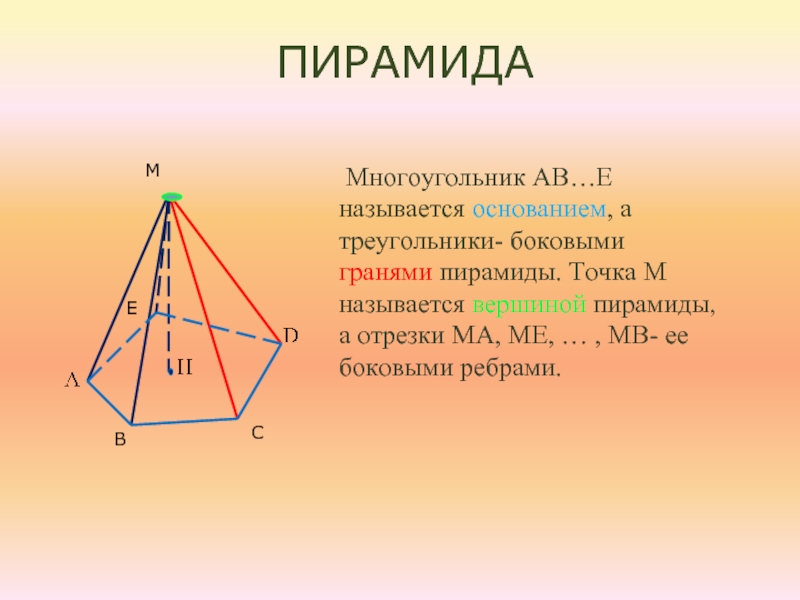
Слайд 4 Многоугольник АВ…Е называется основанием, а треугольники- боковыми гранями пирамиды.
Точка М называется вершиной пирамиды, а отрезки МА, МЕ, …
, МВ- ее боковыми ребрами.пирамида
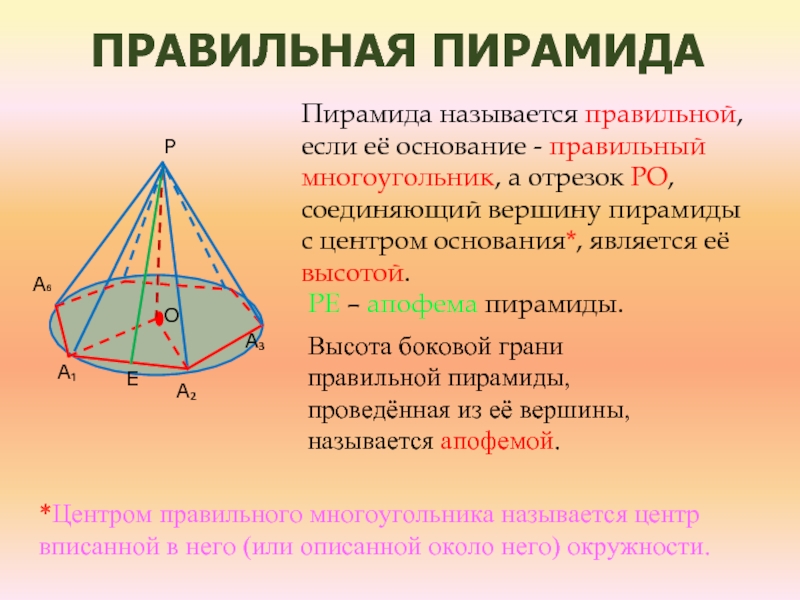
Слайд 5Правильная пирамида
Пирамида называется правильной, если её основание - правильный многоугольник,
а отрезок PO, соединяющий вершину пирамиды с центром основания*, является
её высотой.PE – апофема пирамиды.
*Центром правильного многоугольника называется центр вписанной в него (или описанной около него) окружности.
Высота боковой грани правильной пирамиды, проведённая из её вершины, называется апофемой.
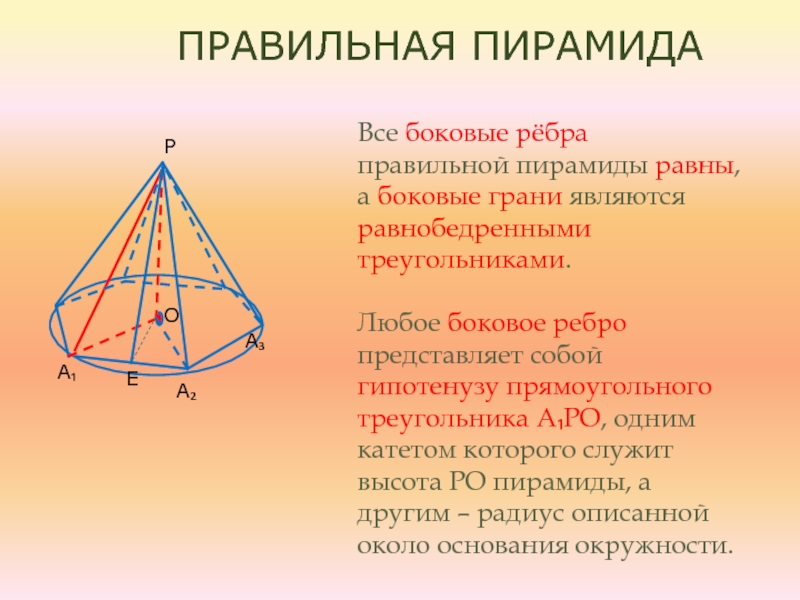
Слайд 6Все боковые рёбра правильной пирамиды равны, а боковые грани являются
равнобедренными треугольниками.
Любое боковое ребро представляет собой гипотенузу прямоугольного треугольника
A₁PO, одним катетом которого служит высота PO пирамиды, а другим – радиус описанной около основания окружности.Правильная пирамида
Слайд 7ТЕОРЕМА:
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания
на апофему.
S
полн = ⅟₂ Pоснов * d
Слайд 8Усечённая пирамида
Многогранник, гранями которого являются n-угольники A 1 A 2…
A n и B 1 B 2… B n (нижнее
и верхнее основание), расположенные в параллельных плоскостях, и n четырёхугольников A 1 A 2 B 2 B 1,A 2 A 3 B 3 B 2,…,A n A 1 B 1 B n (боковые грани), называется усечённой пирамидой.
Отрезки A 1 B 1, A 2 B 2,…,A n B n называются боковыми рёбрами усечённой пирамиды.
Перпендикуляр CО, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды.
P
A 2
A 3
A 1
A n
B n
B1
B 2
B 3
C
Sбок = ⅟₂(P₁ + P₂) * d
Слайд 9Усечённая пирамида
Боковые грани усечённой пирамиды-трапеции.
Усечённая пирамида называется правильной, если
она получена сечением правильной пирамиды плоскостью, параллельной основанию.
Основания правильной усечённой
пирамиды - правильные многоугольники, а боковые грани - равнобедренные трапеции. Высоты этих трапеций называются апофемами. Площадью боковой поверхности усечённой пирамиды называется сумма площадей её боковых граней.
Слайд 10 ТЕОРЕМА:
Площадь боковой поверхности
правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Sбок = ⅟₂(P₁ + P₂) * d
Теги
