выбрать интервал варьирования фактора и количество уровней, на которых необходимо
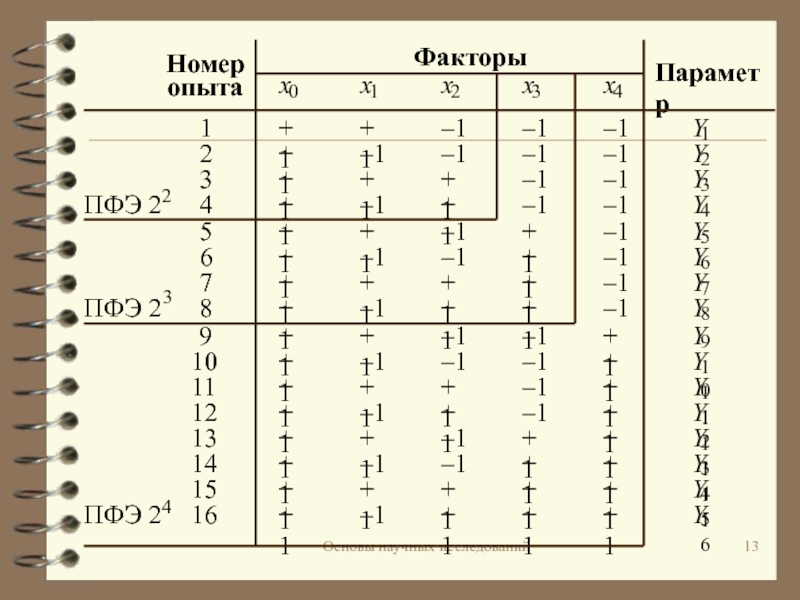
фиксировать факторПланирование многофакторного эксперимента представляет более сложную задачу, поскольку необходимо определить не только интервалы варьирования и количество уровней каждого из факторов, но и порядок их изменения — план эксперимента.





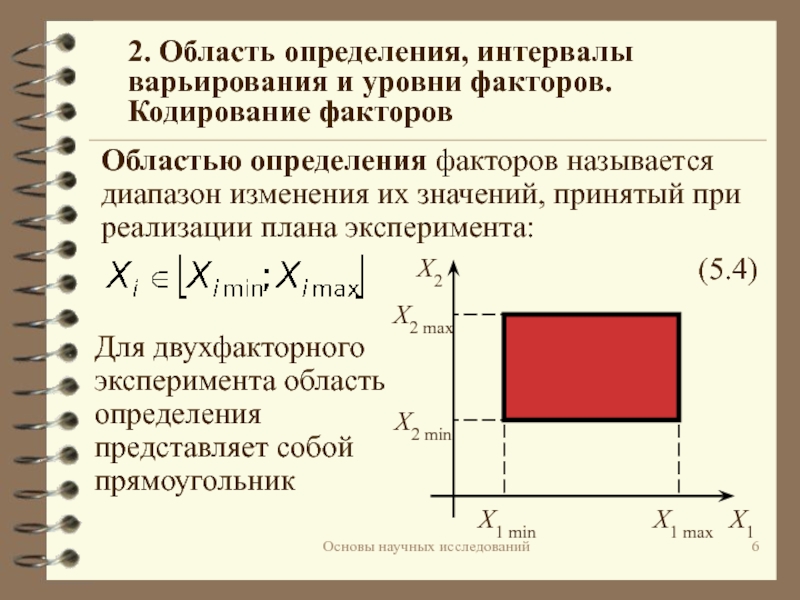
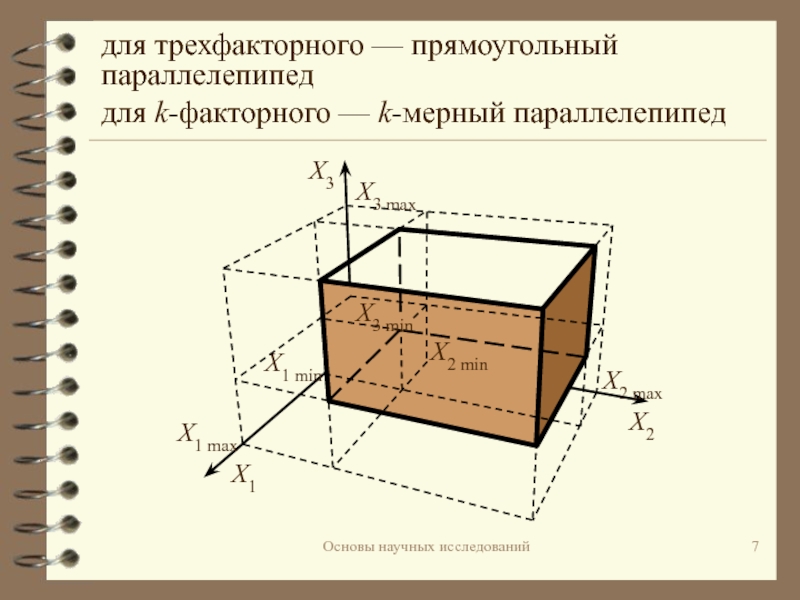

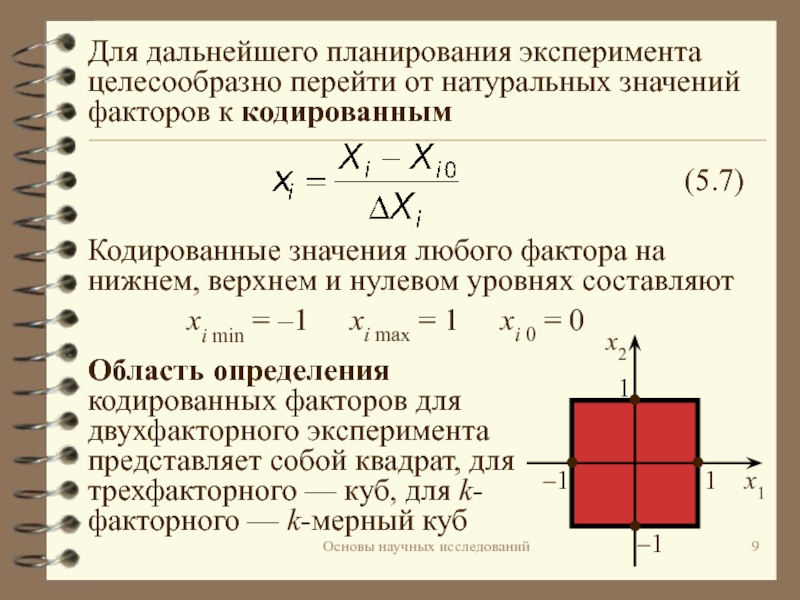

![Планирование эксперимента Основы научных исследованийПоскольку кодированные значения xi безразмерны и изменяются в одинаковых Основы научных исследованийПоскольку кодированные значения xi безразмерны и изменяются в одинаковых интервалах [–1; +1], то все коэффициенты](/img/thumbs/10ebbd47a5ad3e2df37e7b992aaee57e-800x.jpg)