Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Векторная алгебра
Содержание
- 1. Векторная алгебра
- 2. Скалярное произведение векторовМТаким образом, двум векторам: силе
- 3. Скалярное произведение векторовСкалярный квадрат вектора равен квадрату его модуля:Законы скалярного произведения1)2)3)
- 4. Скалярное произведение векторовДля координатных ортов декартовой системы
- 5. Скалярное произведение векторовИз формулы скалярного произведения векторов
- 6. Векторное произведение векторов
- 7. Векторное произведение векторовМодуль вектороного произведения равен площади
- 8. Векторное произведение векторовДля координатных ортов декартовой системы
- 9. Векторное произведение векторов000
- 10. Векторное произведение векторовНайти векторное произведение векторов:
- 11. Векторное произведение векторовНайти площадь треугольника с вершинами:Найдем координаты векторов:АВС
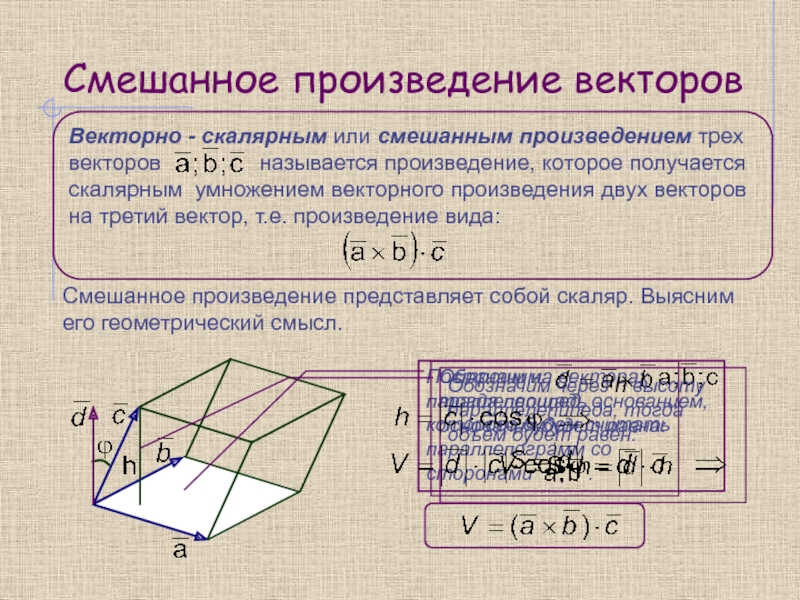
- 12. Смешанное произведение векторовСмешанное произведение представляет собой скаляр. Выясним его геометрический смысл.
- 13. Смешанное произведение векторовВ случае, если векторы образуют
- 14. Смешанное произведение векторовЗаконы смешанного произведения1)2)Сочетательный закон следует
- 15. Смешанное произведение векторов3)Распределительный законВ частности, смешанное произведение
- 16. Смешанное произведение векторов
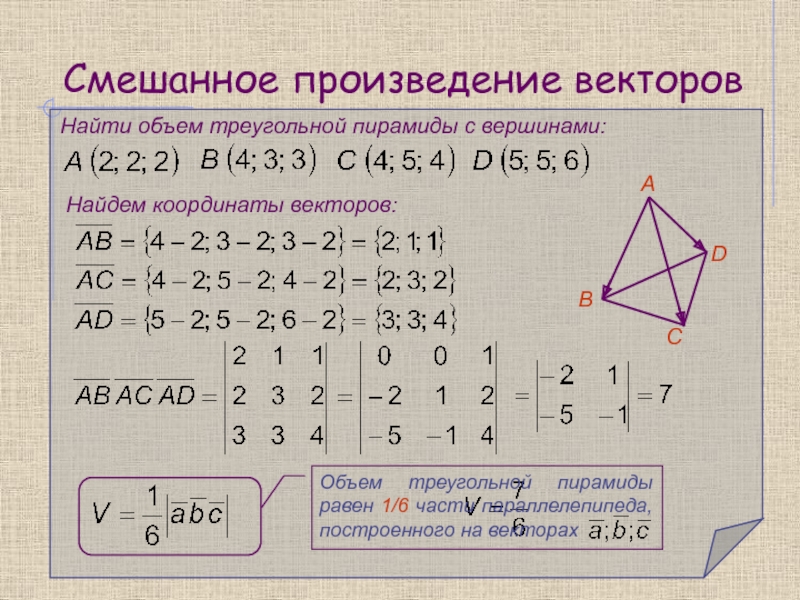
- 17. Смешанное произведение векторовНайти объем треугольной пирамиды с вершинами:Найдем координаты векторов:АВСD
- 18. Скачать презентанцию
Скалярное произведение векторовМТаким образом, двум векторам: силе и перемещению оказался сопоставлен скаляр – работа.Скалярным произведением двух векторов называется произведение модулей этих векторов на косинус угла между ними.
Слайды и текст этой презентации
Слайд 1Векторная алгебра
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Слайд 2Скалярное произведение векторов
М
Таким образом, двум векторам: силе и перемещению оказался
сопоставлен скаляр – работа.
этих векторов на косинус угла между ними.Слайд 3Скалярное произведение векторов
Скалярный квадрат вектора равен квадрату его модуля:
Законы скалярного
произведения
1)
2)
3)
Слайд 4Скалярное произведение векторов
Для координатных ортов декартовой системы координат справедливо:
Пусть в
декартовой прямоугольной системе координат заданы векторы:
Найдем скалярное произведение:
1
1
1
0
0
0
0
0
0
Слайд 5Скалярное произведение векторов
Из формулы скалярного произведения векторов следует формула для
нахождения угла между векторами:
Найти косинус угола между векторами:
Слайд 7Векторное произведение векторов
Модуль вектороного произведения равен площади параллелограмма, построенного на
перемножаемых векторах
Законы векторного произведения
1)
2)
3)
4)
- векторный квадрат равен нулю для любого
вектораСлайд 8Векторное произведение векторов
Для координатных ортов декартовой системы координат справедливо:
Векторное произведение
двух разноименных ортов, следующих друг за другом в направлении положительного
обхода окружности, равно третьему орту со знаком плюс, в противоположном же случае - знаком минус.Пусть в декартовой прямоугольной системе координат заданы векторы:
Найдем векторное произведение: